1257951425

7. TRWAŁOŚĆ ELEMENTÓW Z PĘKNIĘCIAMI

Długotrwała eksploatacja elementów maszyn prowadzona w warunkach pełzania powoduje stopniową degradację materiału. Przejawem tych procesów jest pojawienie się w pewnej fazie eksploatacji pojedynczych mikroszcze-lin, które następnie zaczynają się łączyć doprowadzając zazwyczaj do jednego makropęknięcia. Analizę procesów pełzania we wspomnianym zakresie prowadzi się zazwyczaj opierając się na kontynualnej mechanice uszkodzeń wykorzystującej parametr zniszczenia Rabotnowa-Kaczanowa [50, 82, 84, 93]. Pojawienie się makropęknięcia nie musi oznaczać definitywnego końca pracy elementu. Możliwa jest dalsza eksploatacja, aczkolwiek z rozwijającym się dalej pęknięciem (rys. 7.1) [28, 29].

pękanie

zniszczenie

Rys. 7.1. Procesy zniszczenia i propagacji pęknięć Fig. 7.1. Damage and crack propagation

W podobny sposób możemy również opisać zachowanie się wad istniejących w materiale od początku eksploatacji. Wady te mogą być pochodzenia odlewniczego, mogą też powstawać w wyniku innych procesów technologicznych, np. spawalniczych. Początkowy wymiar tych wad określa się za pomocą badań nieniszczących, a w przypadku niewykrycia takich wad, wymiar ich przyjmuje się na poziomie czułości aparatury pomiarowej.

W niniejszym rozdziale przedstawiono zagadnienie zacnowama się elementu z pęknięciem w warunkach pełzania. Analizę prowadzono opierając się na omówionym w pkt. 4 ogólnym probabilistycznym modelu trwałości. Również i w tym przypadku możemy wyróżnić:

- model deterministyczny obejmujący definicję i sposób wyznaczenia wielkości charakteryzujących stan naprężenia wokół pęknięcia, a także

model propagowania pęknięcia do wymiarów krytycznych,

- nu

eryczne n

rozwiązywania

etody rozwiązania

pęknięcia

wejściowych

definicję niezawodności,

- weryfikację modelu wynikami pomiarów rzeczywistego tempa propagacji.

Poniżej przedstawiono te elementy, które ulegają zmianie w stosunku do modelu omówionego w pkt. 4. W szczególności w pkt. 7.1 i 7.2 przedstawiono elementy modelu deterministycznego, w pkt. 7.3. zdefiniowano pojęcie nieza-

pękn

analizy trwałości pękniętej

7.1- Wielkości charakteryzujące stan naprężenia w obrębie pęknięcia

Problematyka rozwoju pęknięć w warunkach ustalonych naprężeń jest tematem szeregu prac prowadzonych od około 20 lat. We wcześniejszych pracach [7, 12, 143] próbowano powiązać tempo propagacji pęknięcia ze współczynnikiem intensywności naprężeń K analogicznie do przypadku obciążeń cyklicznych. Zależność tempa propagacji przedstawiano zazwyczaj w postaci [7, 75, 94]:

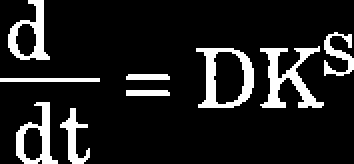
(7.1)

gdzie:

D, S - stałe materiałowe, a - wymiar szczeliny.

Z uwagi na fakt, że zależność (7.1) dobrze opisywała propagację tylko przy małych wartościach wykładnika pełzania (n = 1), a także wykazywała dużą zależność od geometrii badanej próbki, opracowano inną zależność dla analizowanego procesu, wiążącą tempo propagacji z naprężeniem nominalnym

Onet ^[94> ^97]