130859497

Kondunktancja, oznaczana literą G, powiązana z rezystancją R następująco: G = 1/R. Jednostką kondunktancji jest 1S (simens). 1S = 1/Q.

Rezystancja przewodników zależy od temperatury zgodnie ze wzorem:

Rt = Ro[l + a(T-To)J

gdzie:

Ro - rezystancja opornika w temperaturze To,

a - współczynnik temperaturowy rezystancji materiału. Ponieważ a>0, ze wzrostem temperatury rezystancja przewodnika rośnie.

I Prawo Kirchhoffa (prądowe)

Dotyczy ono bilansu prądów w węźle obwodu elektrycznego (rys. 7): suma prądów wpływających do węzła jest równa sumie prądów odpływających od węzła.

I3 + I4 + I5 = 7/ + I2 lub

I5 + I4 + I3 -I/ -I2 = 0, co można zapisać EIk = 0 gdzie: k - liczba gałęzi.

Dla każdego węzła obwodu elektrycznego, algebraiczna suma prądów jest równa zeru.

Prądy wpływające do węzła zapisujemy ze znakiem (+) (I3, I4, I₅), a wypływające ze znakiem (-) (Ii, I2 ).

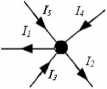
Rys. 7. Węzeł obwodu elektrycznego z oznaczonymi prądami w gałęziach [opracowanie własne]

II Prawo Kirchhoffa (napięciowe)

Suma napięć źródłowych w dowolnym oczku obwodu elektrycznego prądu stałego jest równa sumie iloczynów rezystancji i prądów w gałęziach należących do danego oczka.

R/Ii +R2I2 ~ R3I3 ~ R4I4 ⁼ E1+E2 — E3, E(RI) = EE albo

Ei - R,h +E₂ - R2I2 -E₃ + R3I3 +R4I4 = 0, E(RI) + LE = 0, czyli

W dowolnym oczku obwodu elektrycznego prądu stałego suma algebraiczna napięć źródłowych i napięć odbiornikowych jest równa zeru (rys. 8).

/?/

Rys. 8. Wyodrębnione oczko obwodu elektrycznego [opracowanie własne]

f-

Dla zapisania II prawa Kirchhoffa w postaci równania przyjmujemy pewien (dowolny) zwrot obiegu oczka, oznaczony strzałką wewnątrz oczka, za dodatni. Jeśli zwrot napięcia

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego"

14