1484605289

2.4.2. Ruchliwość warunkowa - więzy bierne

Układ ABCDEF (rys. 20a) jest układem sztywnym - nieruchliwym. To stwierdzenie wynika zarówno z oceny jakościowej, jak i z rozważań strukturalnych (W = 0). Gdy jednak (przy tej samej strukturze układu) dobrać szczególne wartości jego wymiarów podstawowych, np. przyjąć, że AABF = ADCE oraz BC = EF = AD (rys. 20b), otrzymamy układ fizycznie ruchliwy. Można go wykorzystać realnie do przeniesienia ruchu obrotowego wału A na ruch wału D. Zgodnie z dotychczasową umową takiemu układowi należy przypisać W_rz = 1. Tego typu ruchliwość (nie przewidzianą teoretycznie, a stwierdzoną fizycznie) nazywać będziemy dalej ruchliwością warunkową. Zaistnieje ona bowiem tylko wtedy, gdy pewne wymiary podstawowe rozpatrywanego układu spełniają określone warunki. Wtedy niektóre ograniczenia, czyli inaczej więzy, są powtórzeniem już istniejących i fizycznie nie dają o sobie znać. Takie dodatkowe i zbędne kinematycznie ograniczenia nazywa się więzami biernymi. Ich liczbę R_b w łańcuchu kinematycznym można określić, jeżeli znana jest ruchliwość rzeczywista W_rz (ta fizycznie istniejąca) oraz ruchliwość teoretyczna W:

^Rb = ^Wrz ~ ^W    (³)

W analizowanym układzie z rys. 20b jest więc W_rz =1, W = 0, czyli R_b = 1. Do układów kinematycznych, w których R_b> 0 stosuje się określenie układy nieracjonalne. Określenie to wydaje się trafne, zwłaszcza gdy uzmysłowić sobie jak niełatwo spełnić takie narzucone geometryczne warunki ruchu.

Pozostając jeszcze przy układach nieracjonalnych, należy zauważyć dalej, że narzucone tu geometryczne warunki ruchu można w praktyce spełniać tylko z pewnym przybliżeniem. W rezultacie układy te na ogół sprawiają wiele problemów wykonawczych i montażowych. Są przyczyną pojawiania się w układzie dodatkowych obciążeń, zwiększonego zużycia itd. [15], [23].

Ze względu na duże znaczenie omawianych problemów związanych z tymi więzami biernymi zostaną rozpatrzone dalsze przykłady.

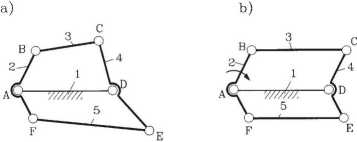
Rys. 20. Ilustracja pojęcia więzów biernych