3218343581

LABORATORIUM PKM

Temat: Wyznaczanie charakterystyki elementów podatnych

Gdy sprężyna śrubowa (rys. 3) obciążona jest osiowo siłą P i moment działający w płaszczyznach oparcia sprężyny o powierzchnie dociskające Mt= 0 (tzn. zakładając, że końce sprężyny nie są utwierdzone i spoczywają na płaszczyznach dociskających bez tarcia), w dowolnym przekroju prostopadłym do osi drutu występują:

-    moment M = PD/2 o wektorze leżącym w płaszczyźnie prostopadłej do osi sprężyny

-    siła P skierowana równolegle do osi sprężyny.

Składowe styczne i normalne tego momentu i siły mają postać:

M_x = M cos y/    Px = P sin y/

M_y — M sin y/    P_y = P cos y/

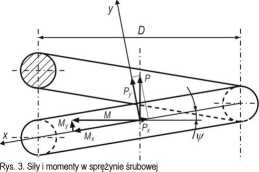
Moment M_x wywołuje skręcanie drutu względem jego osi, a moment M_y powoduje zginanie. Siła P_x powoduje ściskanie drutu wzdłuż osi, a siła P_y powoduje ścinanie w płaszczyźnie prostopadłej do jego osi. Ponieważ kąt pochylenia zwojów sprężyny jest zwykle nie większy niż 9°, a najczęściej nie przekracza 6°, przy obliczaniu naprężeń i ugięcia sprężyny przyjmuje się, że y/ » 0, czyli pomija się naprężenia wywołane zginaniem momentem M_y i ściskaniem siłą P_x, a zamiast P_y i M_x przyjmuje się nieco większe wartości P oraz M. Pomijając działanie

siły ścinającej P_y naprężenie maksymalne w przekroju drutu rmax można opisać zależnością:

, = [MPa]

7id•

Współczynnik poprawkowy K uwzględnia nierównomierność rozkładu naprężeń w przekroju poprzecznym drutu i zależy od wskaźnika (krzywizny) sprężyny w = D/d. Najczęściej oblicza się go wg wzoru Wahla:

K = [(4w-1 )/(4w-4)]+ 0,615/w.

Współczynnik K można również obliczać ze wzoru Góhnera:

K= 1+1,25 (1/w) +0,875 (1/w)²+(1/w)³,

- lub ze wzoru Bergstrassera:

K = (w+0,5)/(w+0,75).

Wskaźnik sprężyny przyjmuje się najczęściej w = 4 + 9.

Strzałkę ugięcia sprężyny oblicza się ze wzoru:

[mm].

, 8P/D³ _r

Gd⁴

Całkowita liczba zwojów sprężyny: gdzie: io= 2- dla sprężyn zwijanych na zimno o zwojach końcowych przyłożonych i szlifowanych lub nieszlifo-wanych, io = 1,5 - dla sprężyn jak wyżej oraz dla sprężyn zwijanych na gorąco o zwojach końcowych przyłożonych i szlifowanych.

Sztywność pojedynczej sprężyny oblicza się ze wzoru:

0=®^ [N/mml.

8 D³/

Obciążenie montażowe sprężyny:

0,1 Pmax — Pmin — 0,5 Pmax-

Instrukcja do zajęć laboratoryjnych 5