6585845001

212

South Africa

TABLE 3

Bearing Capacity Factors

degrees	^Vo	9
5	1,6	0,3
7,5	2,0	0,6
10	2,5	1,0
12,5	3,1	1,4
15	4,0	1,9
17,5	5,1	2,6
20	6,5	3,7
22,5	8,5	5,3
25	11,0	7,3
27,5	14,6	10,4
30	19,5	15,5
32,5	25,5	23,0
35	33,5	34,3
irly all cases,	however,	except pos-

sibly some involving shallow foundations for temporary structures, allowable settlement of the foundation is the controlling factor rather than allowable soil bearing pressure.

Settlement in sand layers has been com-puted from the results of the Dutch cone penetration test using the eguations, given by De Beer and Martens (1957).

medium dense sands. The insitu Buisman-De Beer modulus corresponding to Eąuation (12) is E_s = 1,5 q_c and the effect of Meyerhofs recommendation as evaluated by Schmertmann (1970) is to change this to E_s = 1,9 q_c approximately.

In assessing soil compressibility frora the value of q_c it is necessary to distin-guish as far as possible between normally Consolidated and overconsolidated soils and to take into account density. Since 1966 such procedures have been employed in South Africa for estimation of settle-ments of structures and reclamation fills in areas underlain by estuarine and allu-vial normally Consolidated sediroents using the following relationships given by Webb (1969) in conjunction with the Boussinesq stress distribution.

Fine to medium sands below ground-water level

E' = - (q + 3200) kN/m² (13) 2 ^C

where E* is the reciprocal of my the co-efficient of volume compressibility.

Clayey sands with plasticity index less than 15 percent

Ah 1    pv> + Aov

— = - l°9e - (11)

h C    p_b

+ 1600) kN/m²

(14)

in which C, the constant of compressibi-lity, is computed from the expression

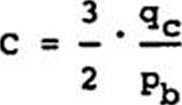
and where h is the thickness of the layer and is the corresponding increase in effective pressure.

Equation (12) is valid for loose sands in which the stress increment Ao^ is smali in relation to p^, and in which Boussi-nesq's theory or stress distribution is applicable. It is based on Buisman*s work on loose sands for which a volume decrease occurs at the penetrometer cone. In many cases, however, this method has overestimated settlements by ratios of up to 1,5 or morę in fine loose to moderate-ly dense sands with shallow ground-water levels. In medium dense clayey fine sands ratios between calculated and ob-served settlements have approached 2,5. For these reasons it is necessary in prac-tice either to modify Equation (12) by replacing the coefficient *4 by a value a which varies with the soil type as sug-gested by Sanglerat (1972) or to employ semi-empirical relationships between cone resistance and compressibility for diffe-rent soils. Meyerhof (1965) has recom-mended increasing the allowable ground bearing pressure calculated from Equa-tions (11) and (12) by 50 percent in fine

Settlements of structures and fills underlain by normally Consolidated loose to medium dense fine sands and clayey sands calculated from Eguations (13) and (14) have been we 11 within the rangę ²/a to V₃ of the observed settlements, the extremes of the rangę being associated with larger settlements in clayey sands which are frequently distributed erratically in the subsoil profiles. Ground bearing pres-sures have generally ranged up to 250 kN/m².

When significant strata of clay are en-countered the usual procedurę is to base settlement predictions on the results of consolidation tests on specimens cut from 100 mm diameter tubę samples, making allowance, in the laboratory my values, for sample disturbance. Because of the advantages of speed and economy prelimi-nary estimates of settlements in clays are soraetiraes madę from the q_c values ob-tained in the Dutch static cone penetrometer tests using Eguation (14). It is found that there is often reasonable agreement between the resulting value of E' and the corresponding laboratory va-lues of my = ^ł/E* when the field values of q_c exceed about 2000 kN/m², although up to the present time no statistical ana-lysis has been madę of such correlations.

For clays of Iow strength yielding Iow values of q , compressibilities have been determined From the undrained shear