8181341979

JVu 12

PRZEGLĄD TECHNK-ZNY

15.H

7_p figur}' płaskiej ograniczonej przoz rzut obwodu na płaszczyznę AA, normalną do p. Mamy więc J = 2/?^, czyli

L,f*^d*=z_v.

Gp    G_p

Gdybyśmy wzięli za s krzywą płaską, a mianowicie w płaszczyźnie normalnej do p, natenczas byłoby poprostu

⁷ =

i

gdzie g jest polem figury płaskiej ograniczonej przez s. Obwód s możemy zresztą zmniejszyć dowolnie, nie zmieniając w niczem powyższego związku.

Przypominając sobie tedy określenie operatora curl*), widzimy z powyższogo, że w naszym wypadku jest

I

i

mi, jednorodnemi składowych .1,, A₃, A_;, wektora JL wzdłuż tychże osi. .Teżeli związek ten zachodzi dla danego układu trzech osi (nie leżących w jednej płaszczyźnie), nie trudno jost. okazać, że będzie też zachodził dla każdego innego układu osi. Jako taki układ odniesienia można wziąć np. układ prawoskrętny normalnych wektorów jednostkowych I, j, h, tak, iż będzie ij = 0 etc., V= h etc.

Symbol działań, które należy wykonać na wektorze AŁ_r aby zeń otrzymać wektor Ji, nazywa się operatorem wektorowym liniowym lub krócej operatorem liniowym. Oznaczymy go wogóle przez co. pisząc więc

JB = co JŁ . . • . . . (XII).

curl t> — 2 p,

czyli curl prędkości wypadkowej dowolnego punktu bryły sztywnej równa się podwójnej prędkości obrotowej tejże bryły, co do wartości bezwzględnej i co do kierunku.

Zobaczymy toż niebawem, że, jeżeli V oznacza prędkość cząstki ciała od kształcą lnego, curl V jest podwójną prędkością wirowania, czyli podwójną prędkością wirową tej cząstki. Stąd też nazwa curl lub ąuirl lub też rotacyu, w skróceniu rot. Nazwę „rotation* zaproponował Maxwj«:ll (El. and Mgnt., t. L); to też H. A. Lorkntz i niektórzy inni autorowie piszą rot\ idąc za Hkaviside‘m i wieloma innymi, pozostaniemy jednak przy symbolu curl.

Operator curl jest identyczny z operatorem Hamilton^ zastosowanym wektorowo, t. j.

curl w = Vy w

Działania, któro operator co symbolizuje, wyrażą się według określenia, przez trzy równania skalarne o dziewięciu współczynnikach skalarnych co_n, co₁₂ etc., a mianowicie:

1

= CO,, A, -|- CO,2 A2 -f* C0_1S A₃ |

B₂ — (o₂₁A, —(~ o).,.,A₂ -j- cojj Aj J . . (XII^a).

⁼⁼ ®3| Aj }- 0>₃₂ Ajj 4“ COjj Aj j

Ogólny operator liniowy określa się tedy przez dziewięć wzajemnie niezależnych danych skalarnych; dane te, np. co_n, co_l2 etc. można zastąpić przez inne dane skalarne, liczba ich jednak nie ulegnie dzięki temu żadnej zmianie. Zamiast dziewięciu skalarnych można wprowadzić trzy dane wektorowe;

; 3 X 3 — 9.

Równanie (XII) jest skrótem ostatnich trzech równań skalarnych. Opuszczając domyślny wektor JL, na którym i mamy operować, można napisać dla samego operatora liniowego

dla dowolnego wektora w, a więc np. przy użyciu składowych prostokątnych w_lt w₂, w₃ wzdłuż kierunków f, j, Ic, stanowiących normalny układ prawoslcrętny wektorów jednostkowych:

curl

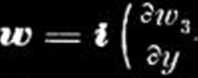
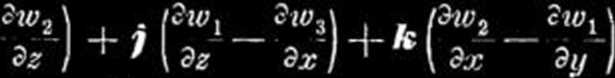
1	co,,	co12	CO,3
i	o>21	C022	^(023
	<*>31	<°32	<*>33

. . (xn^b).

lub też w postaci wyznacznika:

' i ) k i

curi w = Vv w = _t V, V₃ .    .    (XI),

, ^w\ U>2 Wj

gdzie Vi etc. są składowemi V, czvli V, =S!?x, etc. (por. np. El. i Mgnt., str. 43).

Opierając się na (XI) i pisząc tv = v — t?₀ -f- Vpr, czytelnik sprawdzi łatwo związek (48), skoro tylko będzie pamiętał, że V₀₎ p odgrywają rolę stałych.

Mechanika ogólna ciał odkształcalnych.

W dziedzinie zagadnień, do których obecnie przejdziemy, odgrywa nader ważną rolę operator wektorowy liniowy, z którym zapoznaliśmy się już po części przy rozważaniu ruchu bryły sztywnej. Wówczas jednak chodziło zawsze tylko o operator symetryczny, a więc posiadający osie główne wzajemnie prostopadło. Dla ciał odkształcalnych operator ten nie wystarcza; tu spotkamy się już z operatorem liniowym ogólnym, t. j. wogóle niesymetrycznym. Aby zaś nie wstrzymywać pochodu myśli, zestawimy najpierw zasadnicze jego własności. Zbadanie ich, po Hamiltonue, byk) głównie za- . sługą J. W. Gibhs’a; dość szczegółowo wyłożył je Hbaviside w znakomitej swej książce elektromagnetycznej '*).

Poświęcając przedmiotowi temu, czysto matematyczne-mu, osobny rozdział (niewielki zresztą), uprościmy sobie i skrócimy w znacznej mierze wywody dotyczące odkształceń.

Własności operatora wektorowego liniowego.

Wektor JB nazywa się krótko liwoioą funkcyą wektora uAy jeżeli składowe jego B_if B_2> B_z wzdłuż trzech dowolnych, byle tylko nie koplanarnych osi są funkeyami liniowe-

¹ Aby stąd otrzymać U = co Al, należy w całej pierwszej kolumnie umieścić A,, podobnie w drugiej i trzeciej A₂, względnie A₃; pierwszy wiersz, po skojarzeniu jego wyrazów znakami -j-, daje -Z?,, podobnie drugi J?₂, trzeci B_z.

Jeżeli zachodzą równości

^W23 — ⁽⁰32 J .    ⁽⁰31 ~    3 J ^wl2 ^{= W}21 J

natenczas operator liniowy nazywa się symetrycznym, sam zaś wektor JB— m A. funkcyą (liniową) symetryczną wektora JL. i Operator symetryczny oznaczać będziemy wielką literą nie dodając już żadnych dalszych objaśnień. Operator Q będzie określony przez 9 — 3 = sześć danych skalarnych wzajemnie niezależnych, np. przez sześć współczynników Q..,

Qj₂, Ujj, Q₂.V Możemy napisać.    ”

	s12	"" 13
IV II	s,2

Przekątnia ramy, łącząca ,, i ₃₃, stanowi oś symetryi całej tablicy; pamiętając o tein, nie mamy potrzeby wypełniać miejsc pustych.

Przestawiając wskaźniki w operatorze ogólnym co, a więc pisząc co₂, zamiast co_l2 i t. d., otrzymujemy inny operator liniowy co', który nazywa się sprzężonym względem co. Stosuuek ten polega oczywiście na wzajemności, t. j. co jest też sprzężonym względem co'. Operator ił jest samosprzężo-nym\ według jego określenia jest nowiem Q₂i — ^12 ^etc-

Niechaj i ó oznaczają dwa dowolne operatory liniowe; przypuśćmy, że:

JB = <p A. -j- A.;

możemy wówczas napisać

*) Por. jedno z powyżej cytowanych dzieł o wektorach lub też „Elektryczność i Magnetyzm*, str. 28.

^a) ./. 1l^r. (iibbs: Vector Analysis. (Not. published). Newhaven 1881-4.

WiUon: Vector Analysis, etc., fonuded upon the lecture* of ./. W. (ribbs. .New-York & London. 1902.

HcncUide, loc. cit. §§ 198 — 173.

:

U = CO JLy

rozumiejąc mianowicie przez co operator liniowy, którego współczynniki są równo sumie odpowiednich współczynników operatorów cp, c|>, t. j.:

“n = 'Pu + łtn

<*>12 = <Pi2 + łl2t ^etC-i