9988995776

Próbny egzamin maturalny z matematyki. Poziom rozszerzony 3

Zadanie 11. (0—3) Na pewną groźną chorobę choruje 1% całej populacji. Przygotowano tani i łatwy w użyciu test na tę chorobę. Test jest wygodny, ale nie jest w pełni dokładny. Test wykrywa chorobę u chorej osoby tylko w 99% przypadków, natomiast test może wskazać, że osoba jest chora, nawet jeśli osoba jest zdrowa, ale zdarza się to tylko w 2% przypadków.

a)    Jakie jest prawdopodobieństwo, że osoba jest zdrowa, mimo że test był dodatni?

b)    Jakie jest prawdopodobieństwo, że jeśli test był ujemny, to testowana osoba była chora?

Zadanie 12. (0—3) a) Udowodnij, że prosta /: 3x + 4y - 19 = 0 jest styczna do okręgów o, i o₂, gdzie

o, : (x-2)² + (y- 2)² = 1 oraz o₂\ (x-6)² + (y-4)² = 9.

b) Obie proste y = 1 i x = 3 są styczne do obu okręgów. Naszkicuj rysunek okręgów o, i o₂, prostej /, prostej y=l i prostej x = 3 w układzie współrzędnych.

Znajdź równanie czwartej prostej stycznej do okręgów o, i o₂. Narysuj ją.

Zadanie 13. (0—3) Udowodnij, że czworokąt mający kolejne boki o długości 21, 15, 7 i 13 może być trapezem. Oblicz jego pole.

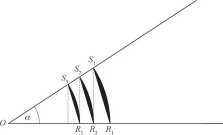
Zadanie 14. (0-3) Pierwszy odcinek koła

0    polu P_{ powstał z okręgu o środku O i promieniu r = 10/^1 = 105,| po odcięciu odcinkiem R_iS_v Drugi odcinek koła powstał następująco: prosta prostopadła do półprostej OR_x

1    przechodząca przez 5, przecina półprostą OR_{ w punkcie R₂. Odcinek S₂R₂ odcina od koła o środku w O i promieniu \OR₂\ = |0S₂| odcinek o polu P₂. Po zatoczeniu luku o środku w O i promieniu OR₂ powstaje punkt S₃ na

półprostej OS_{ itd. powstaje nieskończony ciąg odcinków coraz mniejszych kół. Oblicz sumę nieskończonej liczby wszystkich tych odcinków kół i określ ją jako funkcję a (wyrażonego w radianach) i r.

ln=i Oficyna Edukacyjna * Krzysztof Pazdro