Liczby zespolone
Płaszczyzna zespolona. Rozpatrujemy układ
współrzędnych, w którym na osi pionowej jednostkę
oznaczamy literą i. Oś poziomą nazwiemy osią
rzeczywistą (symbol: Re), zaś oś pionową – osią urojoną
(symbol: Im)
Płaszczyznę z takim układem współrzędnych nazwiemy
płaszczyzną zespoloną.
Każdemu punktowi tej płaszczyzny przyporządkujemy
liczbę zespoloną
yi
x
z
Uwagi
1. Często piszemy też:
iy
x
z
2. Liczbę rzeczywistą x nazywamy częścią rzeczywistą
liczby zespolonej
iy
x
z
i oznaczamy
z
Re
. Zatem:
z
x
Re
3. Liczbę rzeczywistą y nazywamy częścią rzeczywistą
liczby zespolonej
iy
x
z
i oznaczamy
z
Im . Zatem:
z
y
Im
4. Jeżeli
0
Re
z
, to piszemy krótko:
iy
z
(zamiast:
iy
z
0
)
5. Jeżeli
0
Im
z
, to piszemy krótko:
x
z
(zamiast:
i
x
z
0
)
Dodawanie liczb zespolonych
Liczby zespolone dodajemy podobnie jak wielomiany
rzeczywiste, np.:
i
z
3
4
1
i
z
2
1
2
i
i
i
i
z
z
5
3
)
2
3
(
)
1
4
(
)
2
1
(
)
3
4
(
2
1
Liczba przeciwna do liczby zespolonej
iy
x
z
jest to
liczba
iy
x
z
, np.:
i
z
3
4
i
z
3
4
Odejmowanie liczb zespolonych polega na dodaniu do
odjemnej liczby przeciwnej do odjemnika, np.:
i
z
3
4
1
i
z
2
1
2
i
i
i
i
i
z
z
5
)
2
1
(
)
3
4
(
)
2
1
(
)
3
4
(
2
1
Mnożenie liczb zespolonych
Liczby zespolone mnożymy podobnie jak wielomiany
rzeczywiste z tym, że przyjmujemy dodatkową umowę, że
1
2
i
i
i
Przykład 1.
i
z
3
4
1
i
z
2
1
2
i
i
i
i
i
i
i
z
z
5
10
6
5
4
6
3
8
4
)
2
1
(
)
3
4
(
2
2
1
Przykład 2.
Liczbę
i
z
3
4
podniesiemy do kwadratu:
i
i
i
i
i
i
i
i
z
24
7
9
24
16
9
12
12
16
)
3
4
(
)
3
4
(
)
3
4
(
2
2
2
Można też było zastosować wzór skróconego mnożenia
2
2
2
2
)
(
b
ab
a
b
a
i
i
i
i
i
i
i
z
24
7
9
24
16
9
24
16
)
3
(
3
4
2
4
)
3
4
(
2
2
2
2
2
Zapamiętaj:
Wolno stosować wzory skróconego mnożenia.
Liczba sprzężona do liczby zespolonej
iy
x
z
jest to
liczba
iy
x
z
_
, np.:
i
z
3
4
i
z
3
4
_
Dzielenie liczb zespolonych
Aby wykonać dzielenie
2
1
z
z
(gdzie
0
2
z
), mnożymy
licznik i mianownik przez liczbę
2
_
z
(czyli liczbę
sprzężoną do mianownika).
Przykład
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
5
1
25
18
25
5
25
18
16
9
5
18
16
9
12
5
6
)
4
(
3
12
3
8
6
)
4
3
(
)
4
3
(
)
4
3
(
)
2
(
)
4
3
(
)
4
3
(
)
4
3
(
)
2
(
4
3
2
2
2
2
2
Moduł i argument liczby zespolonej .
Modułem liczby zespolonej nazywamy odległość punktu
przedstawiającego tę liczbę na płaszczyźnie zespolonej od
początku układu.
Oznaczenie: r albo
|
| z
Argumentem liczby zespolonej nazywamy miarę kąta
skierowanego od osi rzeczywistej do promienia wodzącego
tego punktu.
Oznaczenie:
albo
z
arg
Z twierdzenia Pitagorasa i trygonometrii wynikają związki:
2
2
y
x
r
r
x
cos
r
y
sin
Postać trygonometryczna liczby zespolonej jest to zapis
tej liczby w postaci
)
sin
(cos
i
r
z
Przykład. Liczbę
i
z
1
zapisać w postaci
trygonometrycznej
Mamy:
1
,
1
y
x
Zatem:
2
1
)
1
(
2
2
2
2
y
x
r
Z rysunku 3 odczytujemy:
o
135
Zatem:
)
135
sin
135
(cos
2
o
o
i
z
Potęgowanie liczb zespolonych
W przypadku wykładnika 2 lub 3 możemy korzystać ze
wzorów skróconego mnożenia, ale w przypadku dużych
wykładników naturalnych wygodniej jest zapisać podstawę
w postaci trygonometrycznej i skorzystać ze wzoru
Moivre’a:
)
sin
(cos
)]
sin
(cos
[
n
i
n
r
i
r
n
n
Przykład. Obliczymy
11
)
1
(
i
W poprzednim przykładzie liczbę
i
1
zapisaliśmy w
postaci trygonometrycznej:
)
135
sin
135
(cos
2
1
o
o
i
i
Stosujemy wzór Moivre’a:
11
)
1
(
i
=
11
)]
135
sin
135
(cos
2
[
o
o
i
)
135
11
sin
135
11
(cos
)
2
(
11
o
o
i
}
45
360
4
1485
{
)
1485
sin
1485
(cos
2
32
o
o
o
o
o
i
2
2
2
2
2
32
)
45
sin
45
(cos
2
32
i
i
o
o
i
i
32
32
2
2
2
32
2
2
2
32
Potęgi liczby i Obliczmy kilka potęg liczby i:
i
i
1
1
2
i
i
i
i
i
i
1
2
3
1
3
4
i
i
i
i
i
i
i
i
i
i
1
4
5
1
5
6
i
i
i
i
i
itd.
Zauważmy cykliczność wyników. Cykl ma długość 4.
Zatem np.
i
i
i
i
1
1
4
8
33
i
i
i
i
3
3
20
4
83
Pierwiastkowanie liczb zespolonych
n
z jest to taka liczba zespolona w, że
z
w
n
.
Jeżeli
0
z
, to jedyną taką liczbą jest 0.
Jeżeli
0
z
, to istnieje n takich liczb. Znajdujemy je ze
wzoru:
n
k
i
n
k
r
w
n
k
2
sin
2
cos
dla
1
,...,
1
,
0
n
k
Przypomnienie:
o
180
Przykład. Obliczmy
i
Zapiszmy liczbę i w postaci trygonometrycznej. Z
rysunku odczytujemy:
o
r
90
,
1
. Stopień pierwiastka
2
n
, zatem są dwie takie liczby.
Podstawiając
0
k
otrzymamy:
2
180
0
2
90
sin
2
180
0
2
90
cos
1
0
o
o
o
o
i
w
0
0
45
sin
45
cos
1
i
2
2
2
2
i
Podstawiając
1
k
otrzymamy:
2
180
1
2
90
sin
2
180
1
2
90
cos
1
1
o
o
o
o
i
w
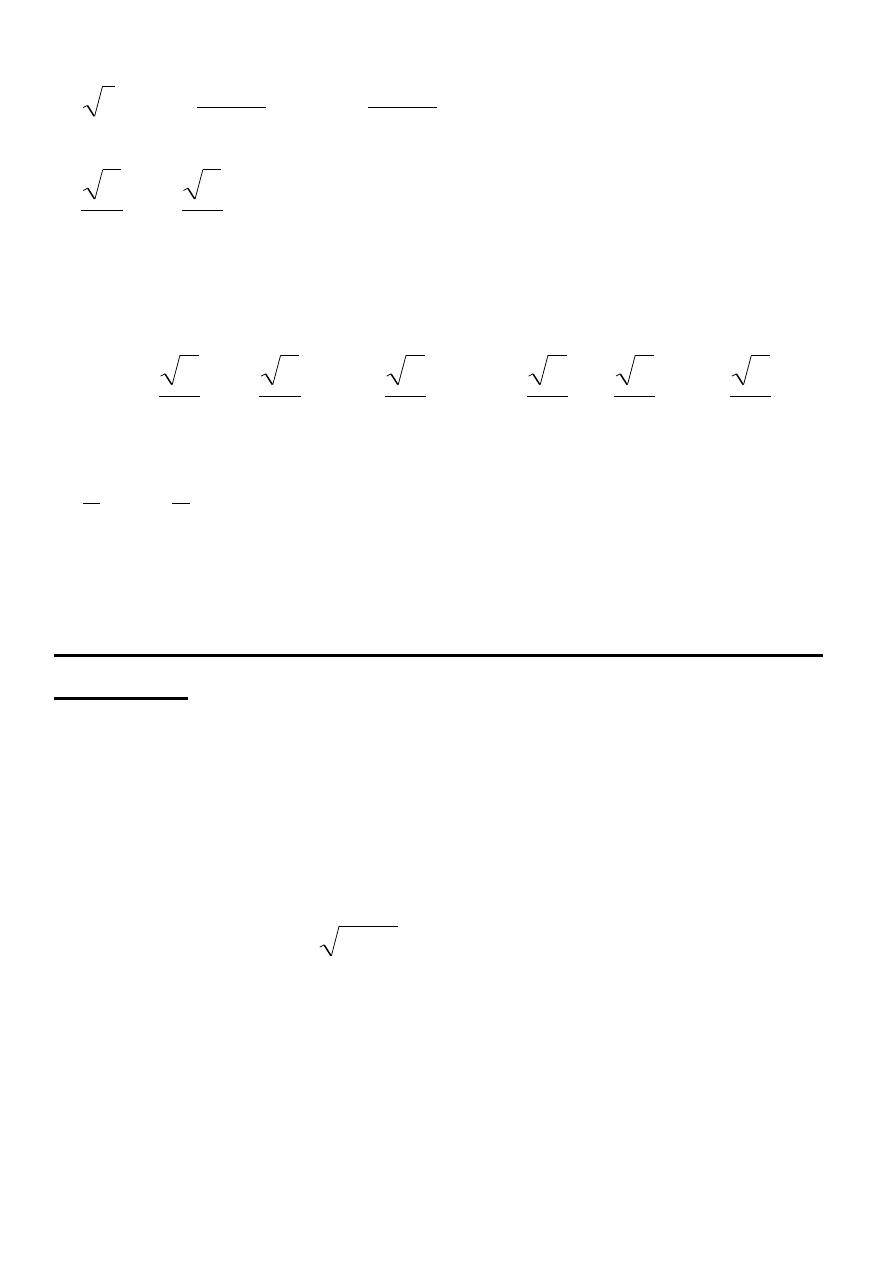
0
225
sin
225
cos
2
450
sin
2
450
cos
1
i
i
o
o
o
=
2
2
2
2
i
Sprawdźmy (dla przykładu), że istotnie np.
i
w
2
0
:
2
2
2
2
0
2
2
2
2
2
2
2
2
2
2
2
2
2
i
i
i
w
i
i
2
1
2
1
Pierwiastki kwadratowe (zespolone) z liczb rzeczywistych
ujemnych
Zauważmy, że każda liczba rzeczywista różna od zera ma
dwa pierwiastki zespolone (stopnia 2). Można je znaleźć
tak jak w poprzednim przykładzie – ze wzoru. Można je
jednak prosto odgadnąć.
Przykład: Obliczyć
25
.
Wiemy, że są dwie takie liczby. Ponieważ
25
5
2
, a
1
2
i
, zatem jedną z nich jest
i
w
5
0
. Ponieważ także
25
)
5
(
2
, zatem
i
w
5
1
Rozwiązywanie równań kwadratowych w zbiorze liczb
zespolonych.
Jak wiadomo w zbiorze liczb rzeczywistych równanie
kwadratowe
0
2
c
bx
ax
, dla którego wyróżnik
ac
b
4
2
jest ujemny – nie ma rozwiązań.
Inaczej jest w zbiorze liczb zespolonych – tam także takie
równanie ma 2 rozwiązania.
Przykład. W zbiorze liczb zespolonych rozwiązać
równanie
0
10
2
2
z
z
Obliczmy:
36
10
1
4
4
4
2
ac
b
Zatem
i
6
lub
i
6
.
Rozważmy najpierw przypadek
i
6
.
Wówczas – ze znanych wzorów – mamy:
i
i
a
b
z
3
1
2
6
2
2
1
i
i
a
b
z
3
1
2
6
2
2
2
Zauważmy, że gdybyśmy wzięli
i
6
,
otrzymalibyśmy te same wyniki.
Zatem równanie ma 2 rozwiązania:
i
z
i
z
3
1
,
3
1
2
1
.
Sprawdzenie. Podstawmy do lewej strony danego
równania w miejsce niewiadomej z liczbę
i
3
1
:
0
10
6
2
9
6
1
10
6
2
)
3
(
6
1
10
)
3
1
(
2
)
3
1
(
10
2
2
2
2
i
i
i
i
i
i
i
z
z
Sprawdź samodzielnie, że również liczba
i
3
1
spełnia
dane równanie.