METODY NUMERYCZNE

Gliwice 2010

wykład

www.kwmimkm.polsl.pl

Interpolacja funkcji

Gliwice 2010

Definicja interpolacji

Gliwice 2010

Dana jest funkcja

 





0

,

,

.

n

y

f x

x

x x





Znamy tablice wartości

tej funkcji, czyli:

 

 

 

 

0

0

1

1

i

i

n

n

f x

y

f x

y

f x

y

f x

y








Wyznaczamy funkcję W(x)

spełniającą warunki:

 

 

 

 

0

0

1

1

i

i

n

n

W x

y

W x

y

W x

y

W x

y








Definicja interpolacji

Gliwice 2010

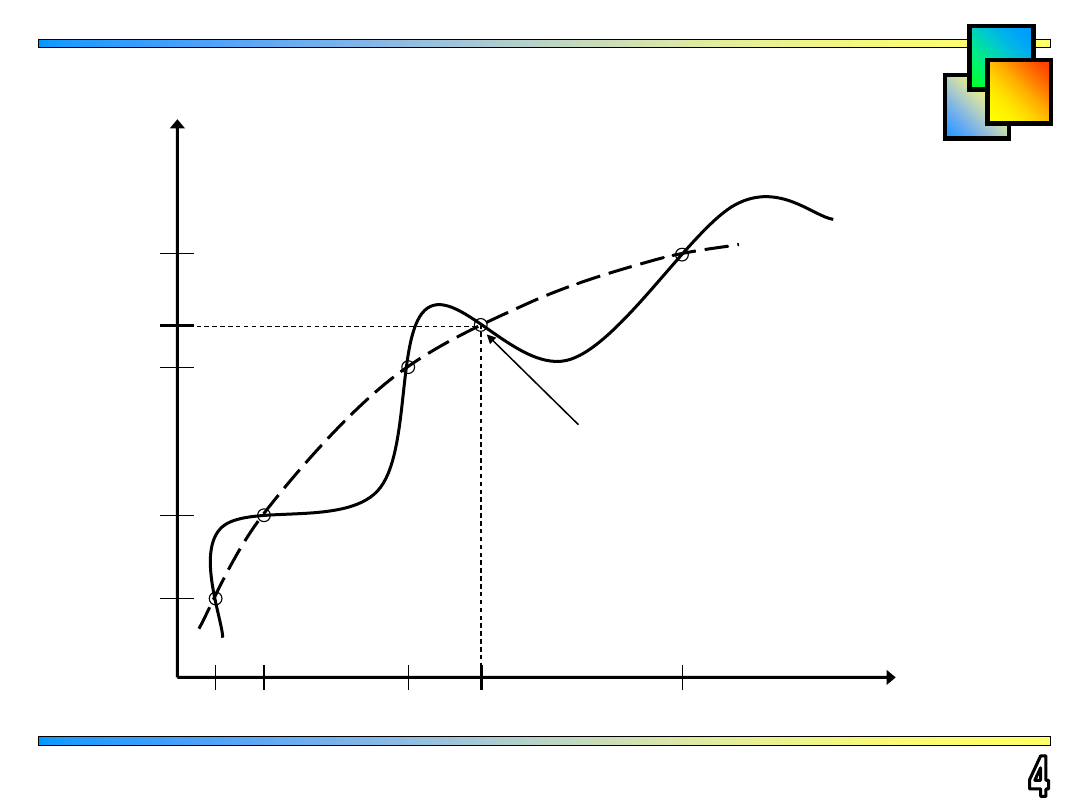
Definicja interpolacji

x

0

x

1

x

2

x

i

x

n

x

y

0

y

1

y

2

y

i

y

n

y

f (x)

W(x)

i - ty węzeł interpolacji

Gliwice 2010

Wyznaczenie funkcji W(x)

Dobór w postaci kombinacji liniowej n +1 funkcji bazowych

Funkcje bazowe:

     

 

 

0

1

2

φ

,φ

,φ

, ...,φ

, ...,φ

i

n

x

x

x

x

x

Wielomian uogólniony:

 

 

0

φ

n

i

i

i

W x

a

x







a

i

– współczynniki

Definicja interpolacji

Macierz bazową:

     

 

0

1

2

φ

,φ

,φ

, ...,φ

n

x

x

x

x





 



Φ

Wielomian uogólniony można zapisać w postaci:

 

 

W x

x





Φ

A

Wprowadzając:

Macierz współczynników:





T

0

1

2

, ,

, ...,

n

a a a

a



A

Definicja interpolacji

Gliwice 2010

Gliwice 2010

 

,

0,1, 2, ...,

i

i

W x

y

i

n





gdzie:

A – macierz kolumnowa współczynników o (n+1) wierszach
Y – macierz kolumnowa wartości funkcji o (n+1) wierszach
X – macierz o wymiarach (n+1)



(n+1)

Warunek, który musi spełnić wielomian interpolacyjny, czyli:

Można zapisać w postaci macierzowej:

 

X A

Y

Definicja interpolacji

Gliwice 2010

Postać macierzy X i Y:

 

 

 

 

 

 

 

 

 

0

0

1

0

0

0

1

1

1

1

0

1

φ

φ

... φ

φ

φ

... φ

...

...

...

...

φ

φ

... φ

n

n

n

n

n

n

x

x

x

x

x

x

x

x

x































X

0

1

...

n

y

y

y

 

 

 



 

 

 

Y

Definicja interpolacji

Gliwice 2006

Jeżeli det X



0 to:

1







A

X

Y

Podstawiając powyższy wzór do otrzymuje się:

 

 

W x

x





Φ

A

Wielomian interpolacyjny:

 

 

1

W x

x









Φ

X

Y

gdzie:



(x)

– macierz bazowa

X

-1

– macierz interpolacyjna

Y

– wektor wartości funkcji w węzłach

Definicja interpolacji

Gliwice 2010

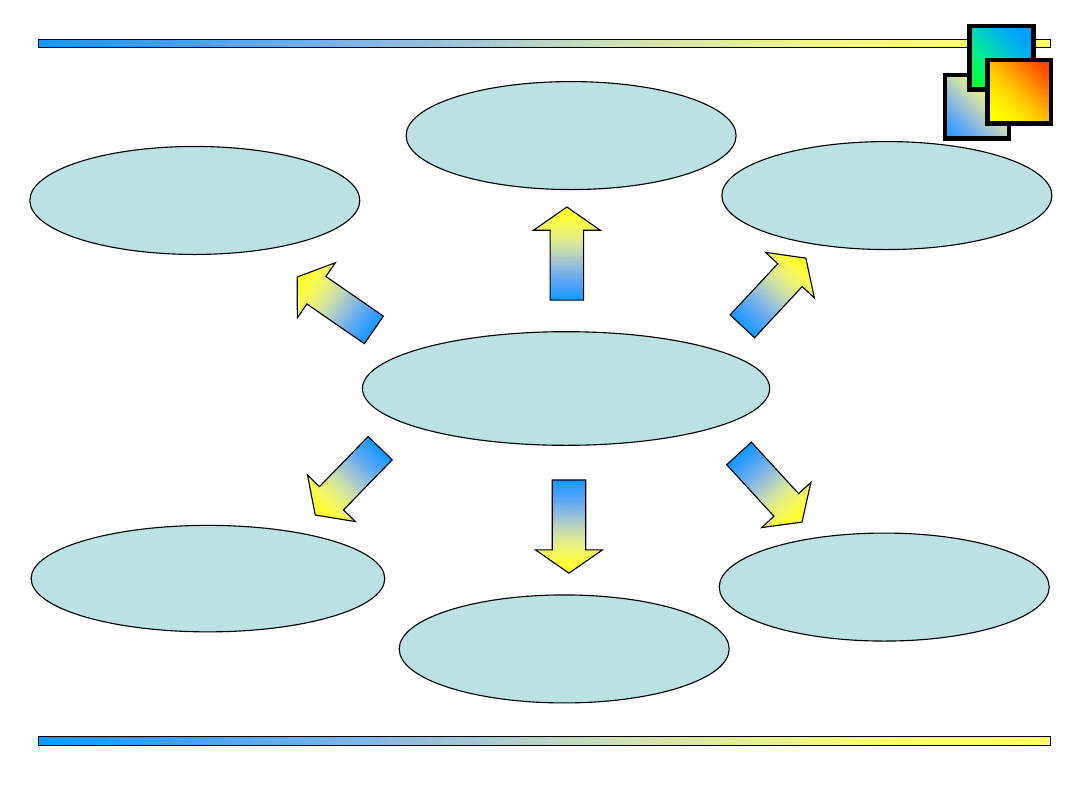
INTERPOLACJA

Interpolacja

WIELOMIANOWA

(NATURALNA)

LAGRANGE’A

NEWTONA

(I WZÓR)

CZEBYSZEWA

TRYGONOMETRYCZNA

NEWTONA

(II WZÓR)

Gliwice 2010

Interpolacja wielomianowa

(wielomiany w postaci naturalnej)

Gliwice 2010

Funkcje bazowe:

Postać wielomianu interpolacyjnego:

 

2

0

1

2

...

n

n

W x

a

a x

a x

a x







 

Interpolacja wielomianowa

 

 

 

 

2

0

1

2

φ

1, φ

, φ

, ...,φ

n

n

x

x

x

x

x

x

x









Gliwice 2010

Przy spełnionym warunku:

Taki układ równań, jeżeli wartości x

0

, x

1

, …,x

n

są między sobą

różne posiada jedno rozwiązanie względem a

i

.

Interpolacja wielomianowa

2

0

1 0

2 0

0

0

2

0

1 1

2 1

1

1

2

0

1

2

...

...

...

...

n

n

n

n

n

n

n

n

n

n

a

a x

a x

a x

y

a

a x

a x

a x

y

a

a x

a x

a x

y





 







 







 



Wynika to stąd, że:

0

0

1

1

1

...

1

...

det

0

...

...

...

...

1

...

n

n

n

n

n

x

x

x

x

x

x





X

Gliwice 2010

interpolacja wielomianowa nie jest zbyt efektywna,

ponieważ macierz X jest macierzą pełną

- błędy podczas odwracania

- czas odwracania

Interpolacja wielomianowa

macierz X nie zawsze jest dobrze uwarunkowana

- macierz osobliwa

WADY:

Gliwice 2010

Interpolacja Lagrange’a

Gliwice 2010

Interpolacja Lagrange’a

Funkcje bazowe:

  













 















 













0

1

2

3

1

0

2

3

0

1

1

1

φ

......................

φ

......................

.....................................................................................

φ

...

...

n

n

i

i

i

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x







































 













0

1

2

1

.....................................................................................

φ

......................

n

n

n

x

x

x

x

x

x

x

x

x

x















dla każdej funkcji



i

(x), i = 0, 1, …, n

brakuje składnika

(x – x

i

)

Gliwice 2010

Postać wielomianu interpolacyjnego:

 

 

 

 































0

0

1

1

0

1

2

1

0

2

0

1

1

φ

φ

...

φ

...

...

...

...

n

n

n

n

n

n

W x

a

x

a

x

a

x

a

x

x

x

x

x

x

a x

x

x

x

x

x

a

x

x

x

x

x

x







 





















 









Interpolacja Lagrange’a

Gliwice 2010

Macierz X:

 

 

 

 

0

0

1

1

2

2

φ

0

0

...

0

0

φ

0

...

0

0

0

φ

...

0

...

...

...

...

...

0

0

0

... φ

n

n

x

x

x

x



































X

Interpolacja Lagrange’a

w punkcie

x = x

i

wszystkie funkcje oprócz



i

(x)

zerują się,

ponieważ występuje w nich składnik

(x – x

i

)

Gliwice 2010

Współczynniki wielomianu Lagrange’a wyznacza się ze wzoru:

Interpolacja Lagrange’a

 

X A

Y

Ponieważ macierz

X

ma tylko główną przekątną niezerową to:





 



 











 





 



 

0

0

0

0

1

0

2

0

0

0

1

1

1

1

0

1

2

1

1

1

1

2

1

...

φ

...

φ

...

...

φ

n

n

n

n

n

n

n

n

n

n

n

y

y

a

x

x

x

x

x

x

x

y

y

a

x

x

x

x

x

x

x

y

y

a

x

x

x

x

x

x

x

































Gliwice 2010

Czyli wielomian interpolacyjny możemy zapisać w postaci

Interpolacja Lagrange’a

 











 







 



 



0

1

1

1

0

0

1

1

1

...

...

...

...

n

i

i

n

i

i

i

i

i

i

i

i

i

n

x

x

x

x

x

x

x

x

x

x

W x

y

x

x

x

x

x

x

x

x

x

x



































Gliwice 2010

Różnice skończone

Gliwice 2010

Różnice skończone

Dla funkcji stabelaryzowanej przy stałym kroku

h = x

i+1



x

i

wprowadza się pojęcie

różnicy skończonej

rzędu

k

1

i

i

i

y

y

y



 



 

2

1

2

1

2

i

i

i

i

i

i

i

y

y

y

y

y

y

y









  

 

  





......

 

1

1

1

1

1

0

1

k

j

k

k

k

k

i

i

i

i

i k

j

k

y

y

y

y

y

j









 



 







  

 

 





 





 



Gliwice 2010

Różnice skończone

Na podstawie zbioru wartości funkcji

y

i

= f (x

i

),

x

i+1



x

i

= h = const

buduje się tablicę różnic skończonych

nr

x

y



y



2

y



3

y

0

x

0

y

0



y

0



2

y

0



3

y

0

1

x

1

y

1



y

1



2

y

1

.

2

x

2

y

2



y

2

.

.

3

x

3

y

3

.

.

.

.

.

.

.

.



2

y

n-3

.

.

.

.



2

y

n-2

.

.

.



y

n-1

n

x

n

y

n

Gliwice 2010

Wzory interpolacyjne dla

argumentów równoodległych

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

Dla zbioru węzłów:

0

1

0

2

0

0

,

,

2 , ...,

n

x

x

x

h

x

x

h

x

x

nh













dane są wartości funkcji:

 

 

 

 

0

1

2

,

,

, ...,

n

f x

f x

f x

f x

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

Funkcje bazowe:

 

 

  



  





  





 



0

1

2

3

φ

1

φ
φ

1

φ

1

2

...

φ

1

2

3 ...

1

n

x

x

q

x

q q

x

q q

q

x

q q

q

q

q

n























 

0

x

x

q

h





gdzie:

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

Wielomian interpolacyjny:

 















 



0

1

2

3

1

1

2

...

1

2 ...

1

n

W x

a

a q

a q q

a q q

q

a q q

q

q

n







 



  





 

0

1

2

:

0

:

1

:

2

...

...

:

n

x

x

q

x

x

q

x

x

q

x

x

q

n

















Dla:

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

Postać układu równań z którego wyznacza się współczynniki

a

i

:



 





0

0

1

1

2

2

3

3

1

0

0

0

...

0

1

1

0

0

...

0

1

2

2

0

...

0

1

3

6

6

...

0

... ...

...

...

... ...

...

...

1

1

1

2

...

!

n

n

a

y

a

y

a

y

a

y

n

n n

n n

n

n

a

y



    



    



    



    





    



    



    



    









    





Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

0

0

a

y



0

1

1

a

a

y

 

1

0

a

y



 

0

1

2

2

2

2

a

a

a

y







2

0

2

2!

y

a







0

1

2

3

3

3

6

6

a

a

a

a

y









3

0

3

3!

y

a











0

1

2

1

...

!

n

n

a

na

n n

a

n a

y







 



0

!

n

n

y

a

n







...

...

Gliwice 2010

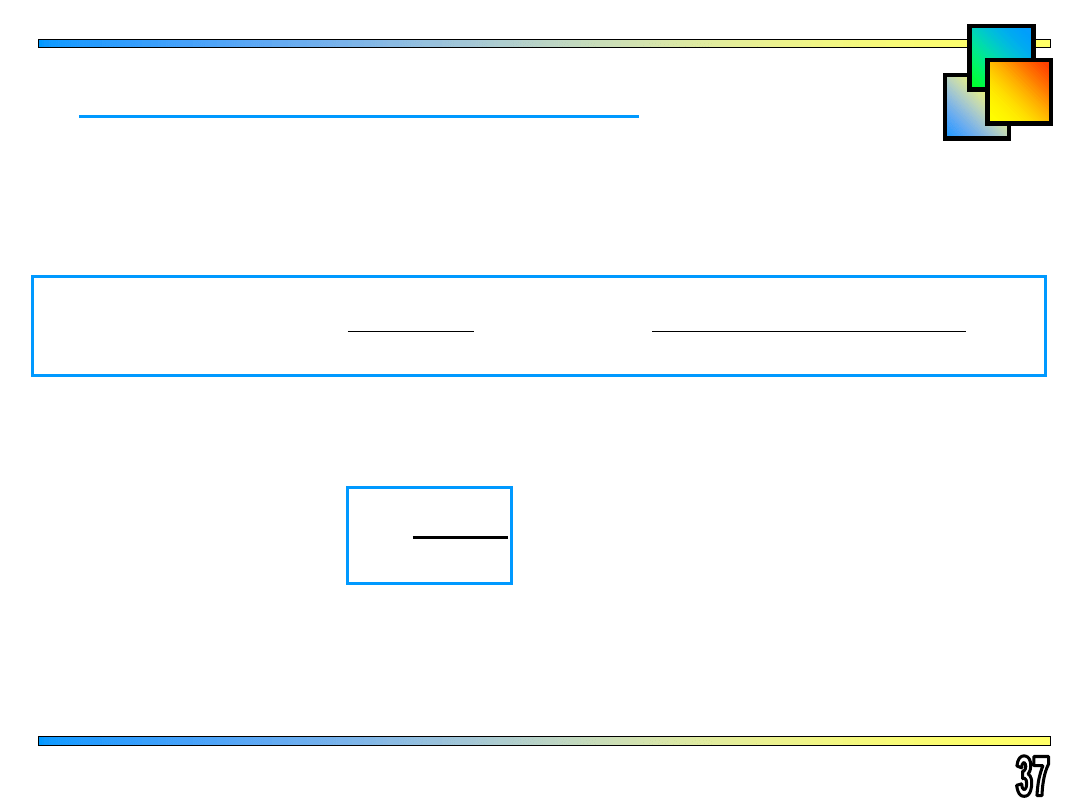
Wzory interpolacyjne dla argumentów równoodległych

I wzór interpolacyjny Newtona

 







 



2

0

0

0

0

1

1 ...

1

...

2!

!

n

q q

q q

q

n

W x

y

q y

y

y

n





 



  



 



0

x

x

q

h





gdzie:

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

I wzór interpolacyjny Newtona - interpolacja w przód

II wzór interpolacyjny Newtona - interpolacja wstecz

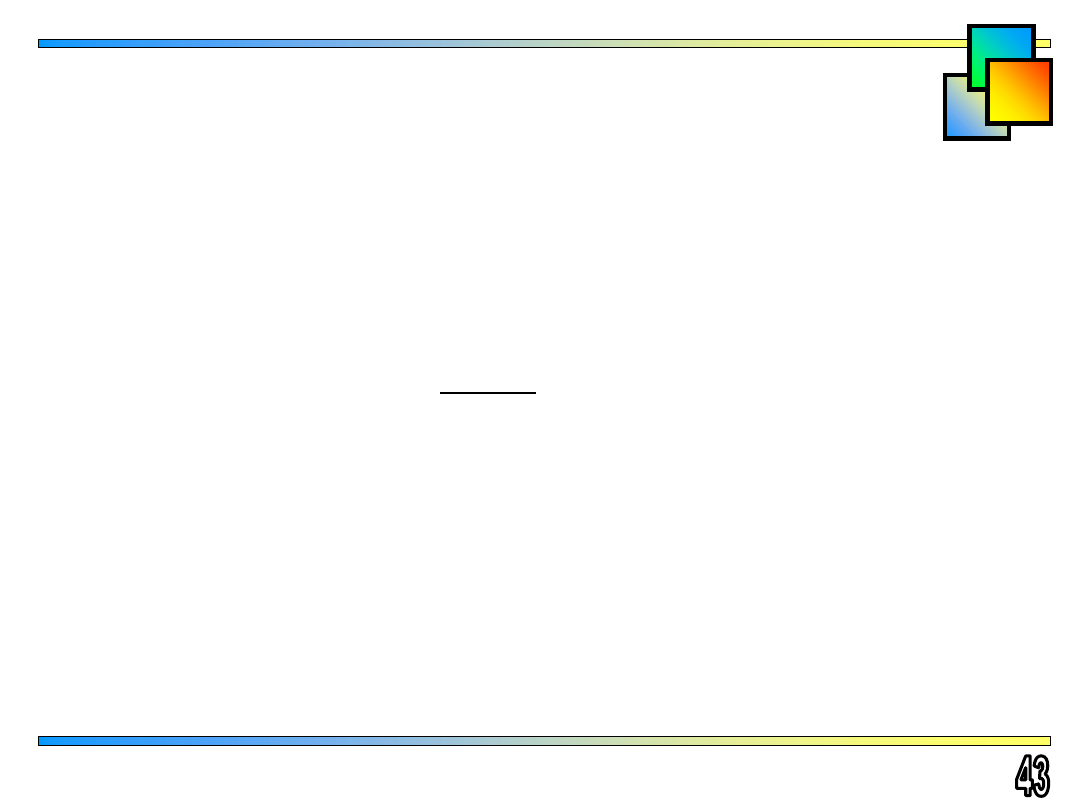
Gliwice 2010

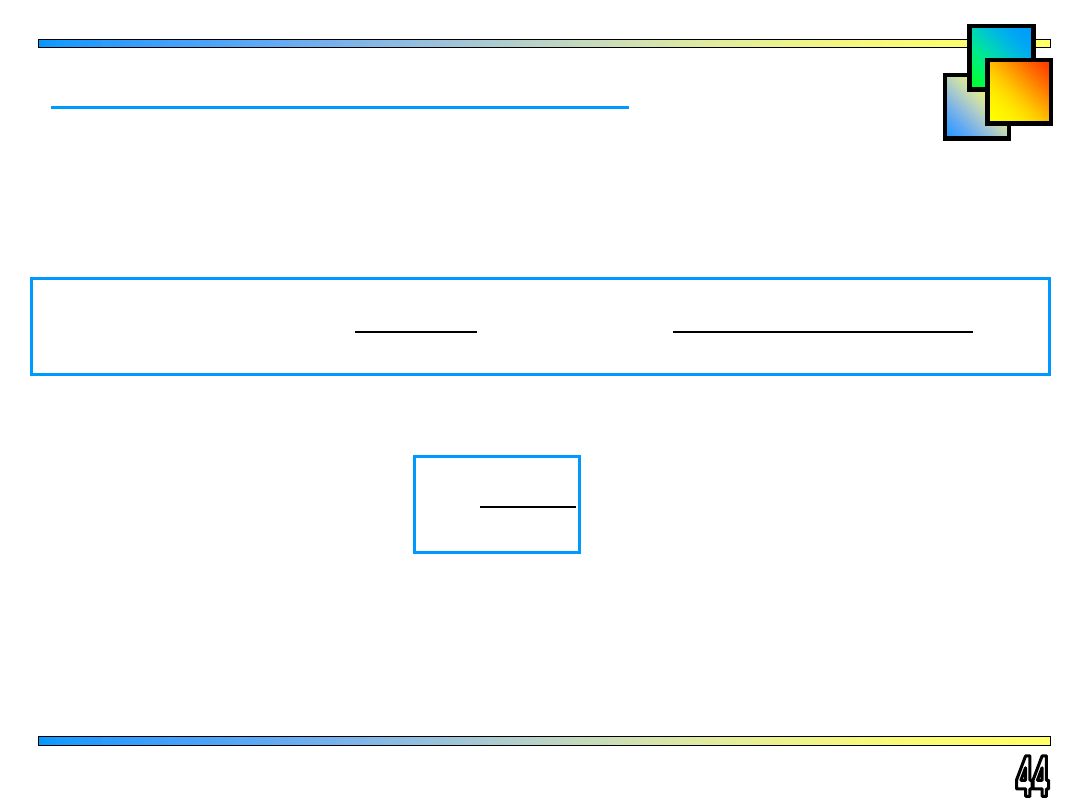
Wzory interpolacyjne dla argumentów równoodległych

Wielomian interpolacyjny:

 















 



0

1

2

3

1

1

2

...

1

2 ...

1

n

W x

a

a q

a q q

a q q

q

a q q

q

q

n







 





 





 

n

x

x

q

h





Współczynniki wielomianu

a

0

, …, a

n

wyznaczane są identycznie

gdzie:

Gliwice 2010

Wzory interpolacyjne dla argumentów równoodległych

 







 



2

1

2

0

1

1 ...

1

...

2!

!

n

n

n

n

q q

q q

q

n

W x

y

q y

y

y

n









 



 





 



II wzór interpolacyjny Newtona

gdzie:

n

x

x

q

h





Gliwice 2010