W

W

y

y

k

k

ł

ł

a

a

d

d

6

6

:

:

I

I

n

n

t

t

e

e

r

r

p

p

o

o

l

l

a

a

c

c

j

j

a

a

f

f

u

u

n

n

k

k

c

c

j

j

a

a

m

m

i

i

s

s

k

k

l

l

e

e

j

j

a

a

n

n

y

y

m

m

i

i

(

(

s

s

p

p

l

l

a

a

j

j

n

n

y

y

)

)

W tym wykładzie omówimy problem interpolacji przy pomocy tzw. funkcji sklejanych,

zwanych też (żargonowo) splajnami. W przeciwieństwie do metod interpolacyjnych

opisanych w Wykładzie nr 1, gdzie stosowaliśmy jeden globalny wielomian dla całego

przedziału interpolacji, w metodzie splajnów stosowane są funkcje zdefiniowane jako

wielomiany niskiego stopnia osobno dla każdego odcinka pomiędzy sąsiednimi węzłami

interpolacyjnymi. Te lokalne wielomiany są jednak tak dobrane, aby – oprócz warunków

interpolacji – spełniać warunki sklejenia w taki sposób, aby cały splajn był funkcją o

odpowiedniej regularności. Skoncentrujemy się przede wszystkim na zagadnieniu interpolacji

za pomocą splajnu kubicznego, tj. funkcji ciągłej wraz z pochodnymi do rzędu drugiego

włącznie i zbudowanej z wielomianów 3-ego stopnia.

Należy wspomnieć, że funkcje sklejane (i ich daleko idące uogólnienia), maja wiele

zastosowań praktycznych, w szczególności stanowią podstawowe narzędzie

współczesnego projektowanie geometrycznego (CAD).

Rozważmy układ

n

węzłów interpolacyjnych

0

0

1

1

1

1

{( ,

), ( ,

),...,(

,

)}

n

n

x y

x y

x

y





, gdzie

0

1

1

..

n

a

x

x

x

b





  



.

Splajnem kubicznym C = C(x) nazywamy funkcje określoną na przedziale [a,b] i taką, że:

1.

2

( )

([ , ])

C x

C

a b



, tj. jest ona ciągła wraz z pierwszą i drugą pochodną w [a,b].

2.

1

3

2

,3

,2

,1

,0

[

,

]

( ) :

( )

k

k

k

k

k

k

k

x x

C x

C x

a x

a x

a x

a













,

0,..,

2

k

n





, tj. wewnątrz każdego

podprzedziału funkcja ta jest pewnym wielomianem 3-ego stopnia.

3. Dla każdego węzła funkcja C(x) spełnia warunki interpolacji tj.

(

)

,

0,..,

1

k

k

C x

y

k

n







.

Z powyższego wynika, że wielomiany lokalne muszą spełniać warunki interpolacyjne

(

)

,

0,..,

1

k

k

k

C x

y

k

n







,

oraz warunki sklejenia zapewniające założoną regularność funkcji C, a mianowicie

1

1

1

(

)

(

)

(

)

(

)

(

)

(

)

k

k

k

k

k

k

k

k

k

k

k

k

C

x

C x

C

x

C x

C

x

C x











 







 







dla

1,..,

2

k

n





(tj. w węzłach wewnętrznych).

Zauważmy, że liczba postawionych warunków jest równa 4n - 6. Całkowita liczba nieznanych
współczynników lokalnych wielomianów jest natomiast równa 4(n - 1) = 4

n

- 4. Zatem,

problem wyznaczenia splajna kubicznego jest niedookreślony.

Potrzebujemy nałożyć dwa dodatkowe warunki tak, aby zagadnienie wyznaczenia
funkcji C miało jednoznaczne rozwiązanie.

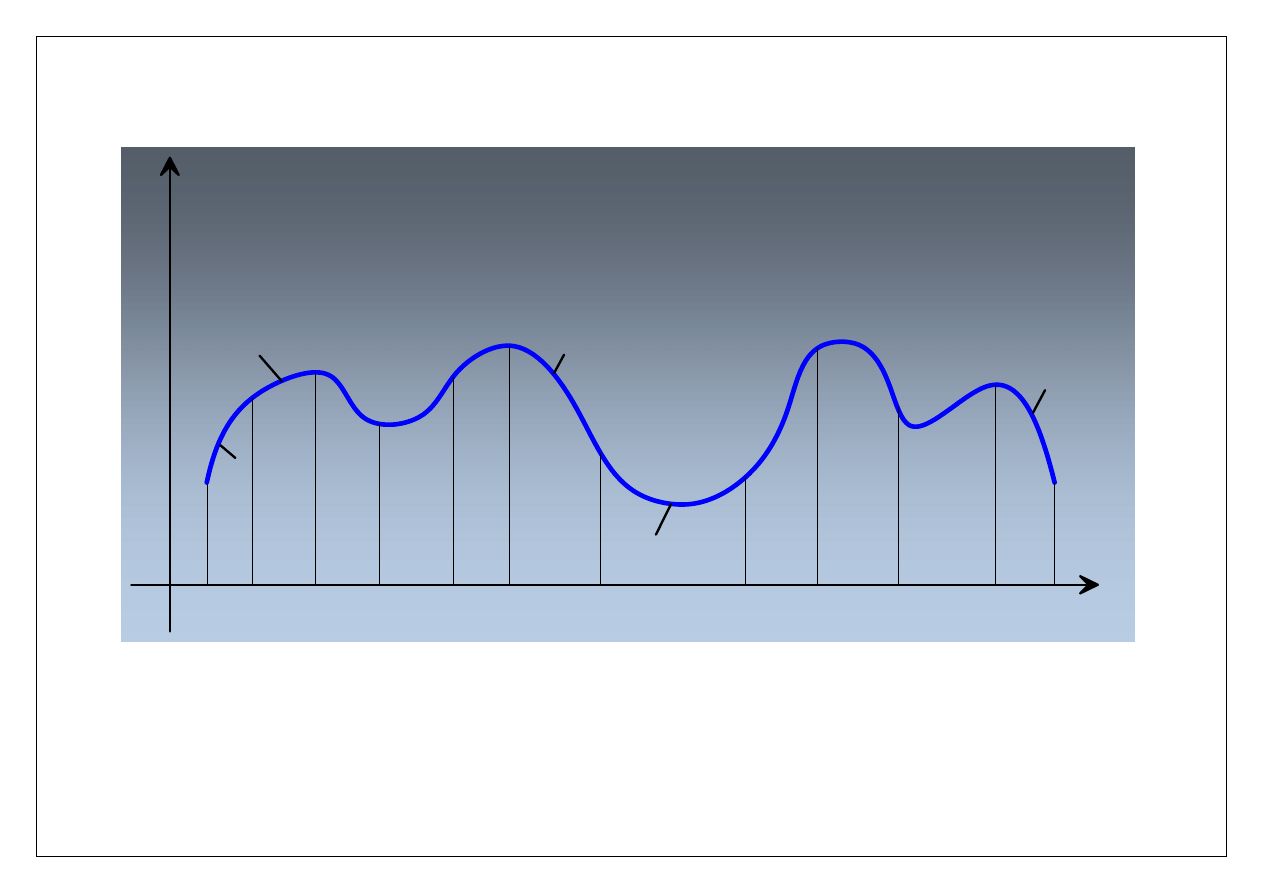
Splajn kubiczny

x

0

x

1

x

2

x

k

x

k-1

x

k+1

x

n-2

x

n-1

y

0

y

1

y

2

y

k-1

y

k

y

k+1

y

n-2

y

n-1

C

1

(x)

C

0

(x)

C

k-1

(x)

C

k

(x)

C

n-2

(x)

y

x

Zwykle (ale nie zawsze) warunki dodatkowe mają formę warunków „brzegowych”
nałożonych na pierwszą lub drugą pochodną funkcji C, a mianowicie:

(

0

(

)

C x







lub

0

(

)

C x







) i (

1

(

)

n

C x









lub

1

(

)

n

C x









)

W powyższych warunkach liczby α, β, γ, i δ są oczywiście zadane.

Ważnym przypadkiem szczególnym jest tzw. splajn naturalny. Jest to taki splajn kubicznym
który spełnia warunki postaci

0

(

)

0

C x





,

1

(

)

0

n

C x







Splajn naturalny posiada interesującą własność. Okazuje się, że spośród wszystkich funkcji
ciągłych wraz z dwiema pierwszymi pochodnymi i interpolujących zadany układ węzłów
splajn naturalny ma najmniejszą wartość całki z kwadratu drugiej pochodnej na
przedziale interpolacji [a,b], tj.

2

( )

min

b

a

C x

dx















Dokładniej, mamy następujące

TWIERDZENIE: Niech

2

0 ,

1

( [

] )

n

f

C

x

x





będzie dowolna. Załóżmy, że

( )

0

C a





i

( )

0

C b





lub

( )

( )

C a

f a







i

( )

( )

C b

f b







. Wówczas

2

2

[

( )]

[

( )]

b

b

a

a

C x

dx

f

x

dx











Dowód:

0

0

( )[

( )

( )]

( )[

( )

( )]

( )[

( )

( )]

( )[

( )

( )]

( )[

( )

( )]

( )[

( )

( )]

przez

czesci

z zal

b

b

x b

x a

ozenia

z zalozenia

a

a

b

a

C x

f

x

C x dx

C x

f x

C x

C

x

f x

C x dx

C b

f b

C b

C a

f a

C a

C

x

f x

C x dx














































































1

1

,3

1

1

1

,3

0

0

6

0

(

)

(

),

0

1

,3

,1 ..

0

, ,

( ) [

( )

( )]

6

[

( )

( )]

6

[ ( )

( )]

0

k

k

k

k

k

k

k

k

k

a

con

n

n

x

x

k

k

x

x

k

k

n

x

st

bo C x

f x

x

k

n

x

k

x

k

C x

f x

C x dx

a

f x

C x dx

a

f x

C x












































 





 















Otrzymaliśmy równość

2

( )

( )

[

( )]

b

b

a

a

C x f

x dx

C x

dx













.

Dalej mamy

2

2

2

2

2

2

[

( )]

0

[

( )

( )]

[

( )]

2

( )

( )

[

( )]

[

( )]

[

( )]

b

a

b

b

b

b

a

a

a

a

b

b

a

a

C x

dx

f

x

C x

dx

f

x

dx

f

x C x dx

C x

dx

f

x

dx

C x

dx



















































czyli

2

2

[

( )]

[

( )]

b

b

a

a

f

x

dx

C x

dx











. Koniec dowodu.

Pozostaje kwestia jak w efektywny sposób wyznaczyć (skonstruować) splajn kubiczny dla
zadanego układu węzłów. W teorii, moglibyśmy zbudować i rozwiązać układ równań
(liniowych) dla nieznanych współczynników lokalnych wielomianów C

k

(k = 0,1,..,n-2).

Układ taki zawierałby 4n-4 równań, a macierz współczynników miałaby dość „paskudną”
strukturę.

Okazuje się (jak zwykle?), że istnieje alternatywna metoda inteligentna!

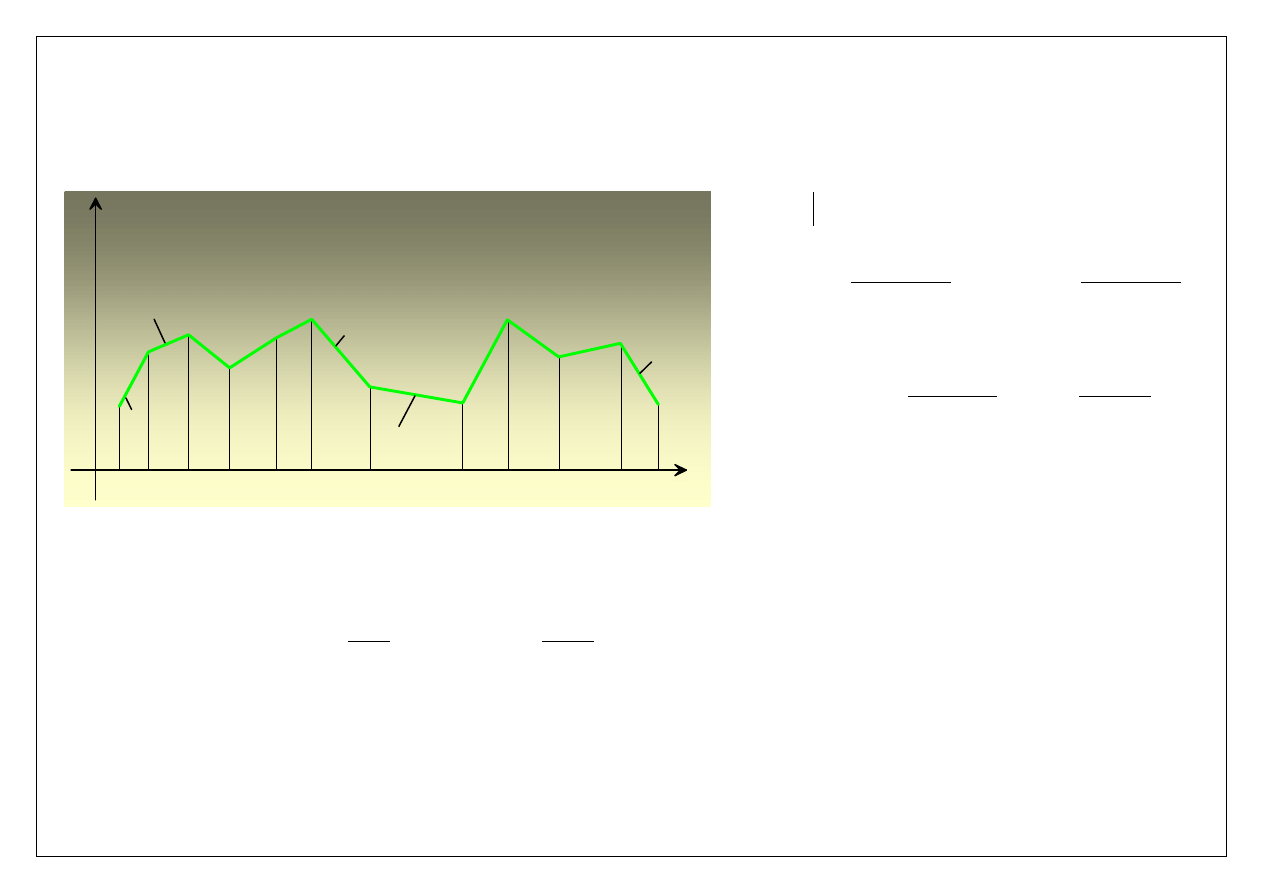
Zacznijmy od spostrzeżenia, że druga pochodna poszukiwanej funkcji sklejanej C jest funkcją
kawałkami liniową (mówimy też – jest splajnem liniowym). Można ją zapisać następująco:

,

1

[

]

1

1

1

1

( )

( )

(

)

(

)

k

k

k

x x

k

k

x

k

x

k

k

k

k

k

C x

C x

x

x

x

x

C x

C x

x

x

x

x



































lub

1

1

( )

k

k

k

k

k

k

k

x

x

x

x

C x

m

m

h

h















gdzie

1

(

) ,

k

k

k

k

k

m

C x

h

x

x











Całkując dwukrotnie powyższą formułę otrzymamy postać lokalnego wielomianu

k

C

3

3

1

1

1

( )

(

)

(

)

(

)

(

)

6

6

k

k

k

k

k

k

k

k

k

k

k

m

m

C x

x

x

x

x

p x

x

q x

x

h

h























przy czym symbole

p

k

i

q

k

oznaczają stałe całkowania. Czytelnik będzie uprzejmy upewnić

się, że druga pochodna funkcji

k

C ma istotnie odpowiednią postać.

x

0

x

1

x

2

x

k

x

k-1

x

k+1

x

n-2

x

n-1

y

0

y

1

y

2

y

k-1

y

k

y

k+1

y

n-2

y

n-1

y

x

L

0

(x)

L

1

(x)

L

k-1

(x)

L

k

(x)

L

n-2

(x)

Póki co, stałe całkowania były dowolne. Teraz dobierzemy je tak, aby spełnić warunki
interpolacji

1

1

(

)

,

(

)

k

k

k

k

k

k

C x

y

C x

y









Otrzymujemy wartości stałych

p

k

i

q

k

2

1

1

6

6

k

k

k

k

k

k

k

k

k

k

y

y

m h

p h

p

m h

h











2

1

1

1

6

6

1

1

1

k

k

k

k

k

k

k

k

k

k

y

y

m h

q h

q

m h

h



















i w konsekwencji ostateczna postać lokalnego wielomianu wyraża się formułą

3

3

1

1

1

1

6

6

1

1

1

( )

(

)

(

)

(

)

(

)

6

6

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

m

m

y

y

C x

x

x

x

x

m h

x

x

m h

x

x

h

h

h

h































 





















przy czym indeks k przyjmuje wartości od 0 do n-2.

Pozostało obliczyć wartości drugiej pochodnej splajnu w węzłach, czyli wielkości

0

1

1

,

,...,

n

m m

m



.

Zauważmy, że nie wykorzystaliśmy jeszcze warunku „dopasowania” pierwszej pochodnej
sąsiadujących wielomianów lokalnych. Różniczkując otrzymaną wyżej formułę dla C

k

mamy

2

2

1

1

1
6

1

1

( )

(

)

(

)

(

)

2

2

k

k

k

k

k

k

k

k

k

k

k

k

k

m

m

y

y

C x

x

x

x

x

m

m h

h

h

h













 













Rozważmy węzeł

x

k

. Z powyższego wzoru wynika dla

k

x

x



, że

1

1

1

1

1

3

6

3

6

1

1

(

)

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

d

y

y

C x

m h

m h

m h

m h

d

h











 





 





Wartość pierwszej pochodnej wielomianu C

k-1

w węźle

x

k

otrzymamy następująco: najpierw

w ogólnej formule dla 1-szej pochodnej wielomianu C

k

podmienimy formalnie k na k-1, a

następnie podstawimy

k

x

x



. Oto rezultat (sprawdzić!)

1

1

1

1

1

1

3

6

3

6

1

1

1

1

1

1

1

1

1

(

)

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

d

y

y

C

x

m h

m h

m h

m h

d

h







































Z warunków ciągłości 1-szej pochodnej w węzłach mamy

1

(

)

(

)

k

k

k

k

C

x

C x









, co po

podstawieniu otrzymanych wzorów i prostych przekształceniach prowadzi do następującego
układu równań dla wielkości

0

1

1

,

,...,

n

m m

m



1

1

1

1

2(

)

,

1,2,..,

2

k

k

k

k

k

k

k

k

h m

h

h m

h m

u

k

n





















gdzie oznaczyliśmy

1

1

1

1

6(

)

6

k

k

k

k

k

k

k

k

k

y

y

y

y

u

d

d

h

h

































.

Wiemy już, że do wyznaczenia funkcji sklejanej C potrzebujemy dwóch dodatkowych
warunków. Jeśli zdecydujemy się na określenie wartości pierwszej pochodnej w węzłach
skrajnych to warunki te przyjmą postać

1

1

3

6

0

0

0

0

1

0

0

0

0

1

0

(

)

2

6(

)

C x

h m

h m

d

h m

h m

d







 















1

1

3

6

1

2

1

2

2

2

2

2

2

1

2

(

)

2

6(

)

n

n

n

n

n

n

n

n

n

n

n

C x

h

m

h

m

d

h

m

h

m

d













































Jeśli natomiast określimy wartości brzegowe drugiej pochodnej to dodatkowe równania są
bardzo proste, a mianowicie

0

m





i

1

n

m







. W szczególności, jeśli

0

 

 

to

otrzymamy splajn kubiczny naturalny.

Podsumowując, kompletny układ równań liniowych dla wartości drugiej pochodnej splajna
kubicznego w węzłach może być zapisany następująco:

0

0

0

0

1

0

1

1

1

1

1

2

2

2

1

2

2

6(

)

,

0

2(

)

,

1,..,

2

2

6(

) ,

1

k

k

k

k

k

k

k

k

n

n

n

n

n

n

m

h m

h m

d

k

h

m

h

h m

h m

u

k

n

m

h

m

h

m

d

k

n

lub

lub



































































 

W notacji macierzowo-wektorowej:



Tm r

. Zauważmy, że macierz

T

jest trójdiagonalna.

Niezerowe elementy tej macierzy można zapisać jako elementy trzech wektorów a,b and c.

0

0

1

1

2

2

2

1

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

k

k

k

n

n

n

n

n

c

b

a

c

b

a

c

b

a

c

b

a

c









































































T

Wartości zapisane w tych wektorach zależą od przyjętego wariantu „warunków
brzegowych” i przedstawiają się następująco:

0

1

1

1

2

0

,

1,..,

2

0

(

)

k

k

n

n

n

nie uzyw

a

a

h

k

n

a

lub

h

y

a

an













  











 



0

0

0

1

0

,

1,..,

2

(

)

0

k

k

n

l

b

b

h

b

h

nie uzuwan

u

b

y

k

n

b





 



  













0

0

0

1

1

1

2

1

2

2(

) ,

1,..,

2

1

2

k

k

k

n

n

n

lub

l

c

c

h

c

h

h

k

n

c

c

ub

h















 

















Do efektywnego rozwiązania układu liniowego z macierzą trójdiagonalną stosujemy
specjalny wariant metody eliminacji Gaussa zwany algorytmem przeganiania (Thomasa).
Przedstawimy ten algorytm zakładając, że rozwiązywany układ równań ma postać

0

0

0

1

0

1

1

1

2

1

1

1

,

1,..,

2

k

k

k

k

k

k

k

n

n

n

n

n

k

n

c m

b m

r

a m

c m

b m

r

a

m

c

m

r















































Metoda przeganiania (algorytm Thomasa)

Rozważmy dwa pierwsze równania układu

0

0

0

1

0

1

0

1

1

1

2

c m

b m

r

a m

c m

b m

r

















i załóżmy, że

0

0

c



. Najpierw „normalizujemy” pierwsze równanie dzieląc je przez c

0

,

następnie eliminujemy m

0

metodą przeciwnych współczynników

0

0

0

0

0

0

0

0

1

0

1

1

0

1

1

2

,

/

,

/

b c

r c

a m

c m

b

m

m

m

r





























i w końcu sprowadzamy zmodyfikowane drugie równanie do postaci „znormalizowanej”

1

0 1

1

1

2

1

1

0

1

0 1

1

1

0

1

1

1

1

0

1

1

2

1

1

0 1

1

(

)

/ : (

)

,

,

c

a m

b m

r

a

c

a

r

a

b

m

a

a

m

c

c



























 

















W trakcie obliczeń pojawiają się dwie pomocnicze wielkości

1



and

1



.

Zauważmy, że nowy zredukowany układ równań z niewiadomymi

1

1

,...,

n

m

m



wygląda „tak

samo” jak oryginalny, tj. ma strukturę 3-diagonalną i pierwsze z równań ma postać 3-
diagonalną i pierwsze równanie ma postać znormalizowaną. Układ ten jest zatem gotowy do
kontunuowania procedury eliminacji kolejnych niewiadomych. Po k krokach procedury
eliminacyjnej dochodzimy do etapu, w którym układ zwiera niewiadome o numerach od k do
n-1. Następny krok polega na eliminacji niewiadomej

m

k

metodą przeciwnych

współczynników. W szczegółach wygląda to następująco

1

1

1

1

1

1

2

1

1

1

1

1

2

1

1

1

1

1

1

1

1

1

1

1

2

1

1

1

/

(

)

,

,

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

k

m

m

a

a

m

c m

b m

r

c

a

m

b m

r

b

r

a

m

m

c

b

a

c

a

























































































































Podczas obliczeń pojawia się kolejna para wielkości pomocniczych

1

k





and

1

k





.

Ostatecznie, po n-1 krokach eliminacji proces osiąga ostatnie równanie układu. Ostatni krok
eliminacji przebiega następująco

2

2

1

2

1

1

2

1

1

1

1

2

1

1

1

1

2

1

1

2

1

1

2

1

/

(

)

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

m

m

a

a

r

b

m

c

m

c

m

r

c

a

m

r

a

b



























































































Zauważmy, że ostatnie równanie układu zawiera jedynie dwie niewiadome (przedostatnią i
ostatnią), przez co wyniku eliminacji m

n-2

otrzymujemy równanie z tylko jedną niewiadomą

m

n-1

. Zauważmy również, że podczas procesu eliminacji otrzymaliśmy rekursywną formułę

wiążącą dwie niewiadome o kolejnych numerach. Ogólna postać tej formuły wynika z
pierwszego równania (znormalizowanego) zredukowanego układu po k krokach eliminacji, a
mianowicie

1

,

2,

3,...,1,0

k

k

k

k

m

m

k

n

n

 







 



W ten sposób wszystkie wyeliminowane wcześniej niewiadome mogą być wyznaczone w
pętli chodzącej wspak.

Metodę przeganiania (algorytm Thomasa) można podsumować następująco:

0

0

0

0

0

0

1

1

1

1

1

1

1

1

1

2

1

1

1

2

1

1

1 (

)

/

;

/

;

0,..,

3

:

;

;

;

2 (

)

;

2,..,

!

:

!

0

k

k

k

k

k

k

k

k

k

k

k

k

n

n

n

n

n

n

n

k

k

k

k

ETAP

sweep

up

b

c

r

c

for k

n

do

b

c

a

r

a

c

a

end

ETAP

sweep

down

r

a

m

c

a

for k

n

ta petla c

do

m

m

hodzi wst

en

ecz



















































































 





;

d

UWAGA:

Ponieważ metoda przeganiania jest pewnym wariantem metody eliminacji Gaussa (bez
wyboru elementu głównego – vide Wykład 7), to na macierz trójdiagonalną należy nałożyć
pewne ograniczenia gwarantujące powodzenie obliczeń. Chodzi przede wszystkim o
gwarancję, że wszystkie operacje dzielenia będą wykonalne (nie wystąpi dzielenie przez
zero).

Można pokazać, że warunki wystarczające dla powodzenia przebiegu obliczeń metodą
przeganiania mają następującą postać:

0

1

0

0

1

1

1)

0,

0 ,

0 ,

0 ,

1,..,

2

2)

,

1,..,

2

,

n

k

k

k

k

k

n

n

c

c

a

b

k

n

c

a

b

i

n

c

b

c

a































Przynajmniej jedna z ty

warunki

ch niero

diagonalnej domina

wnosci musi byc OS

cji

TRA!