MECHANIKA NIEBA

WYKŁAD 14

23.06.2008 r

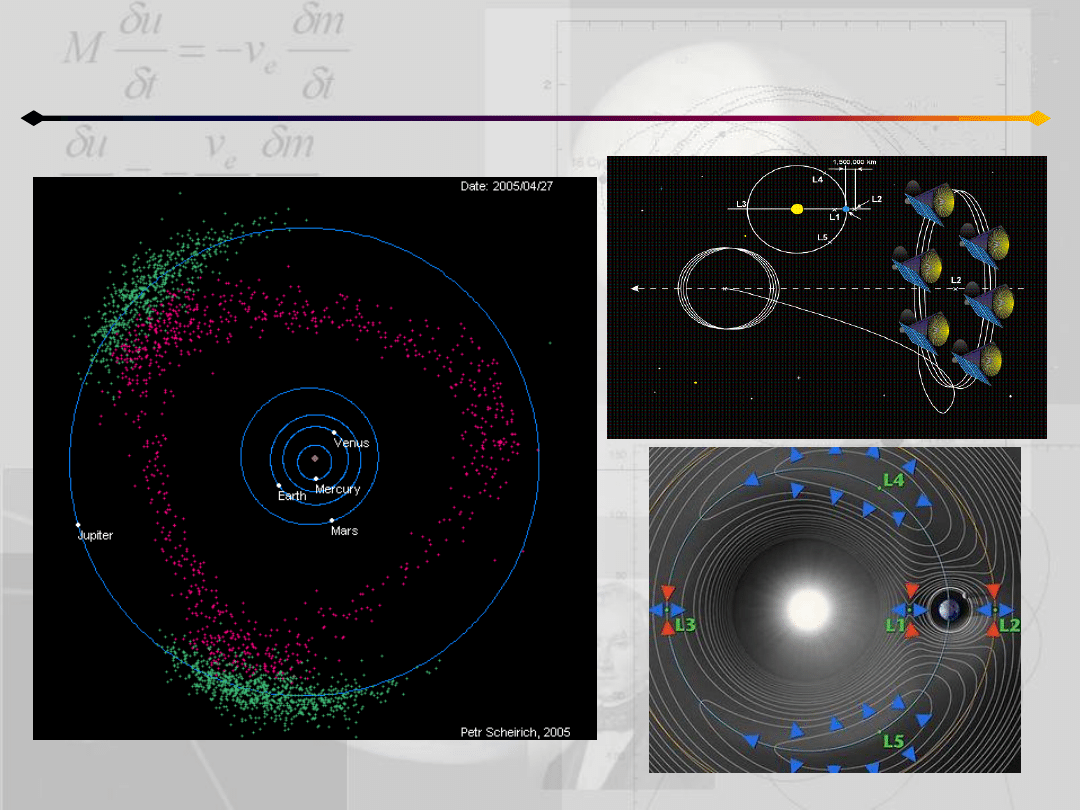
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

www.asc.rssi.ru

sajri.astronomy.cz

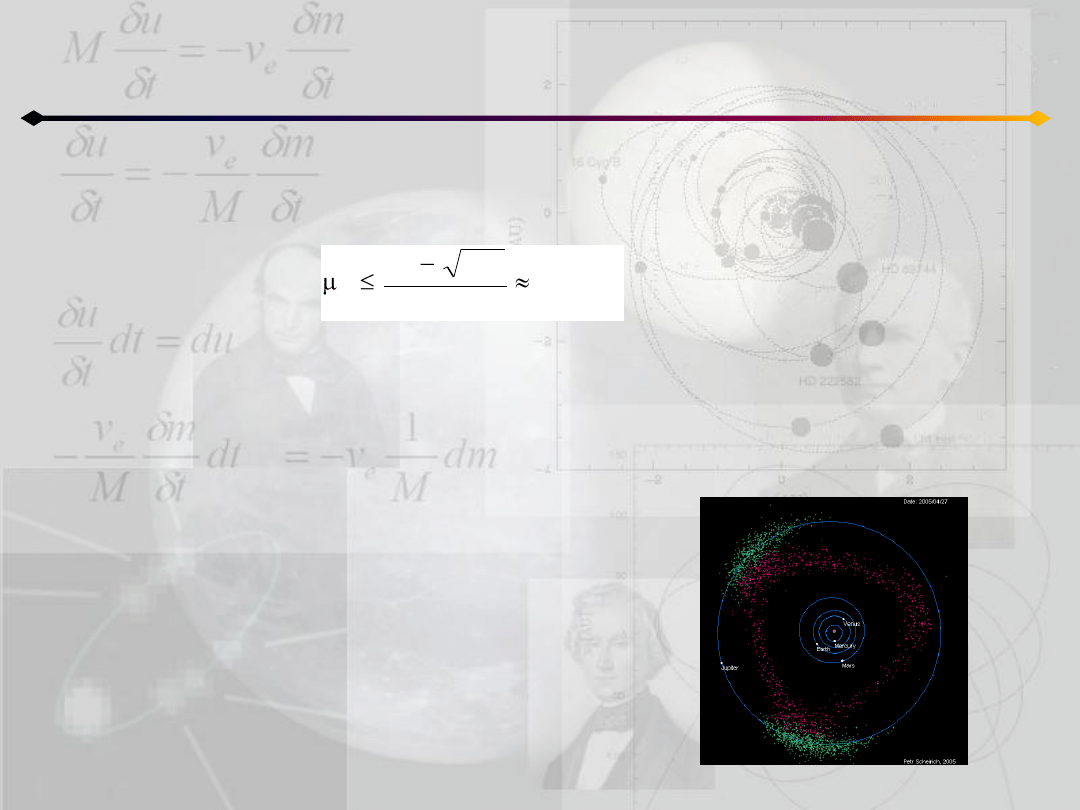
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

0385

.

0

54

621

27

2

Warunek stabilności punktów L

4

i L

5

:

Jest spełniony w Układzie Słonecznym dla wszystkich par Słooce-planeta i
planeta-księżyc, poza parą Pluton-Charon (ale Pluton już nie jest planetą)

W 1906 r. został odkryty pierwszy obiekt poruszający się wokół L

4

układu

Jowisz-Słooce – (588) Achilles

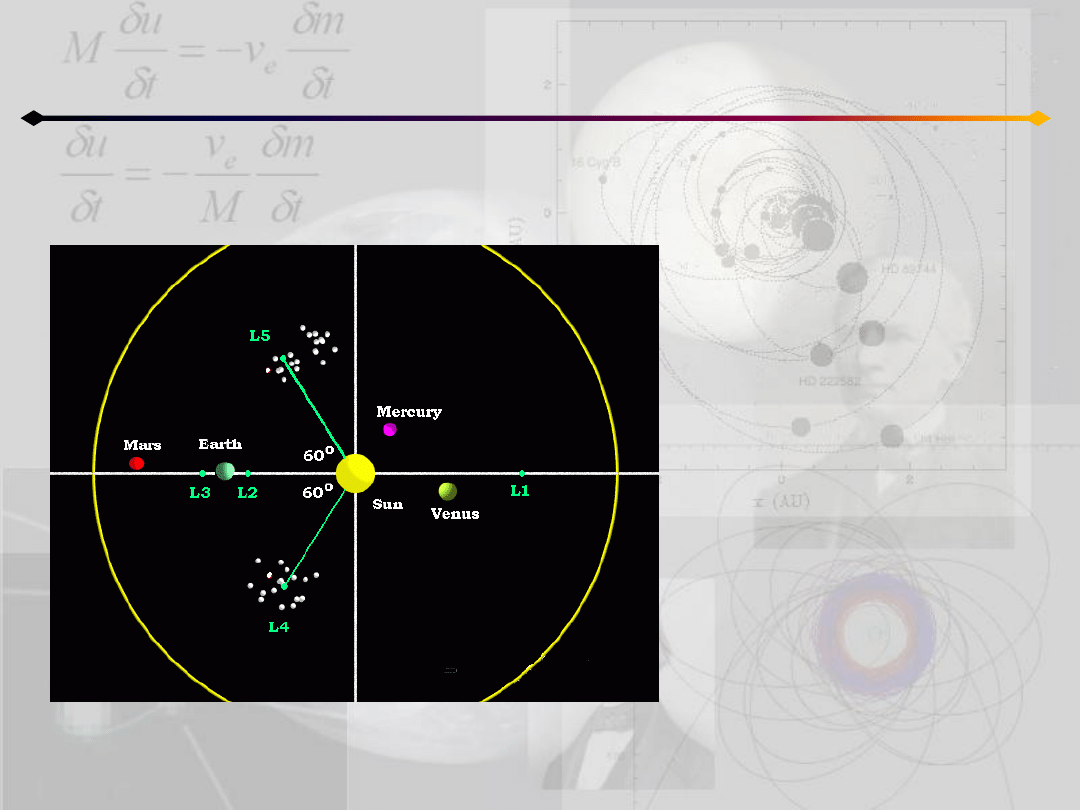
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

Copyright by Paul Wiegert

(3753) Cruithne – pierwszy
obiekt poruszający się wokół
punktu równowagi układu
Ziemia-Słooce

Księżyce Kordylewskiego?

Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

Copyright by Paul Wiegert

Symulacje stabilności obiektów wokół
punktów równowagi układu Słooce-Ziemia

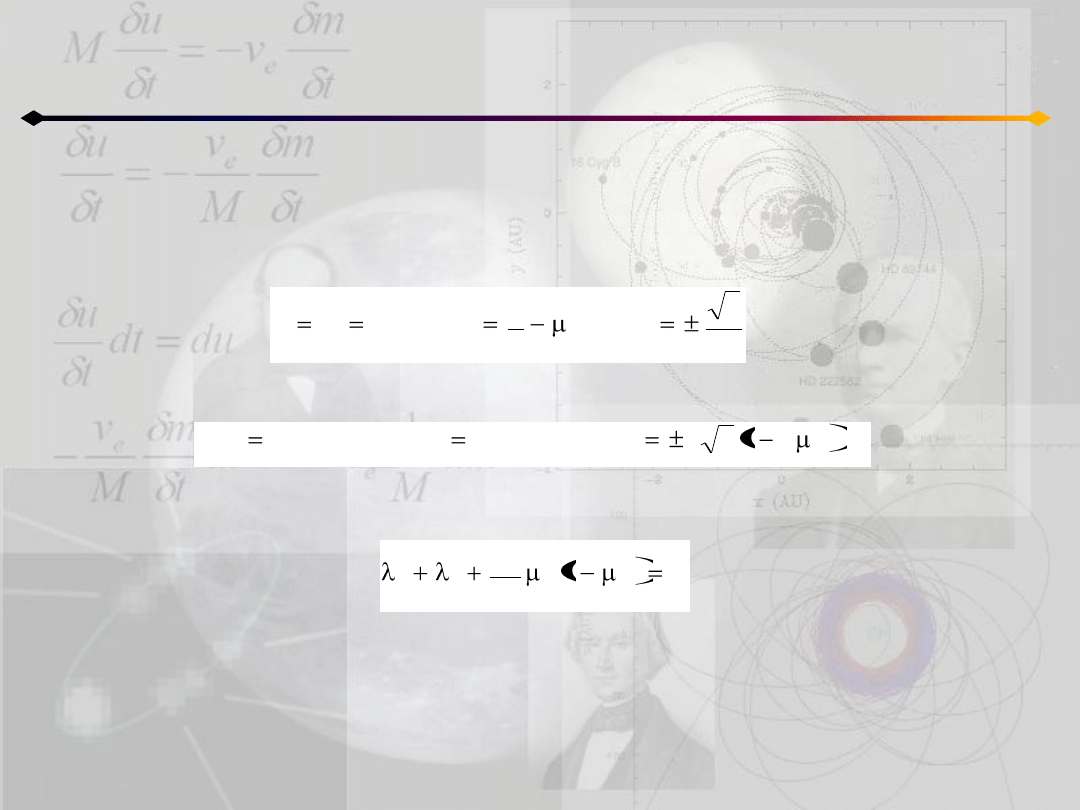
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

W tym wypadku mamy:

skąd:

Równanie charakterystyczne przyjmuje postad:

2

3

y

2

1

x

1

r

r

2

2

1

4

/

2

1

3

3

U

4

/

9

U

4

/

3

U

2

xy

y y

xx

0

1

4

27

2

2

2

4

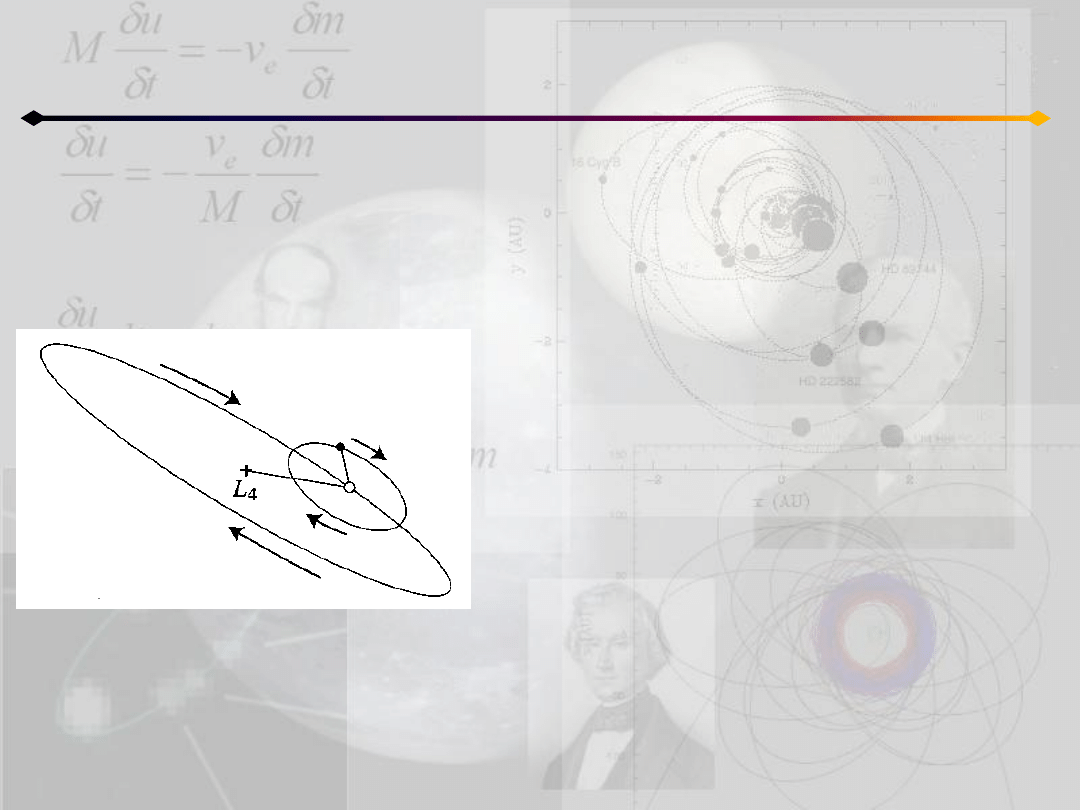
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

Wybraliśmy układ jednostek, w którym ruch średni
masy μ

2

jest jednostkowy, a okres orbitalny = 2π

Ruch cząstki jest złożeniem dwóch ruchów:

- krótkookresowego, okres= 2π/|λ

1,2

| jest zbliżony

do okresu orbitalnego masy μ

2

- libracyjnego wokół punktu równowagi,
okres= 2π/|λ

3,4

|

Amplitudy tych ruchów zależą od stałych α

j

, β

j

,

które zależą od warunków początkowych

Ruch wypadkowy można traktowad jako złożenie
długookresowego ruchu epicentrum wokół L

4

i

krótkookresowego ruchu wokół epicentrum

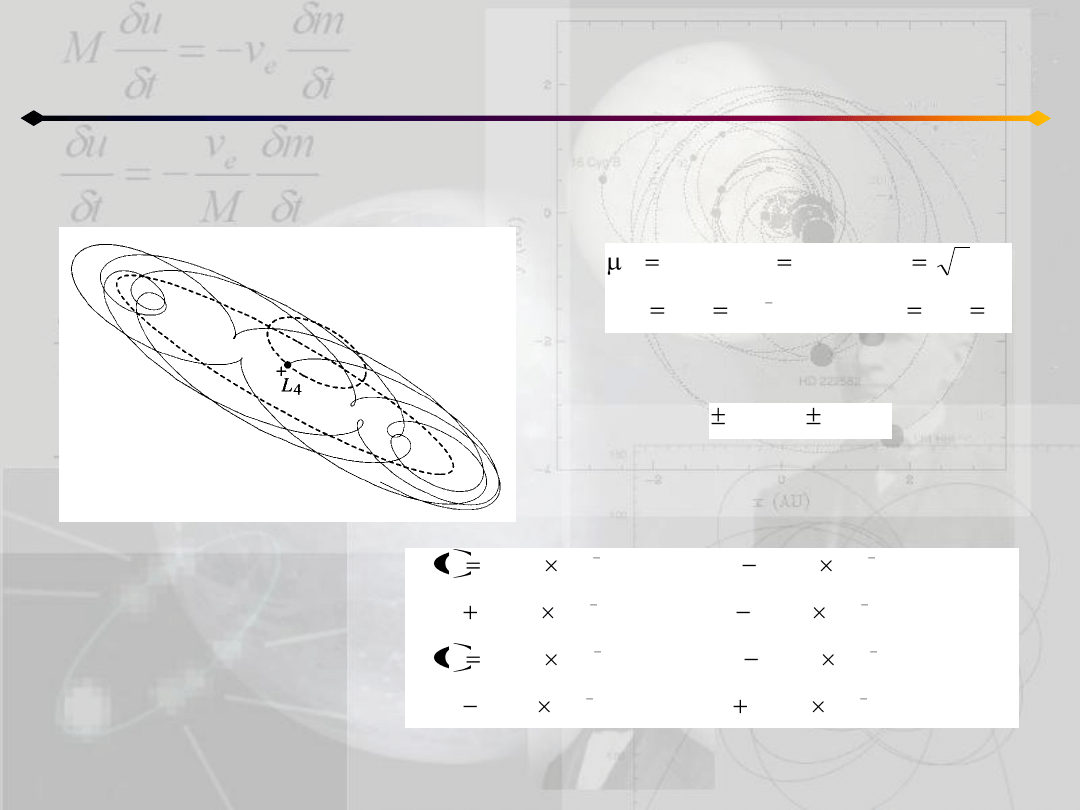
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

Przykład:

odpowiednie wartości własne są równe:

Wtedy rozwiązanie ma postad:

0

Y

X

,

10

Y

X

2

/

3

y

,

49

.

0

x

,

01

.

0

0

0

5

0

0

0

0

2





i

32

.

2

90

.

2

t

963

.

0

sin

10

90

.

4

t

268

.

0

sin

10

76

.

1

t

963

.

0

cos

10

20

.

4

t

268

.

0

cos

10

20

.

5

t

Y

t

963

.

0

sin

10

55

.

8

t

268

.

0

sin

10

07

.

3

t

963

.

0

cos

10

45

.

2

t

268

.

0

cos

10

45

.

3

t

X

5

4

5

5

5

4

5

5

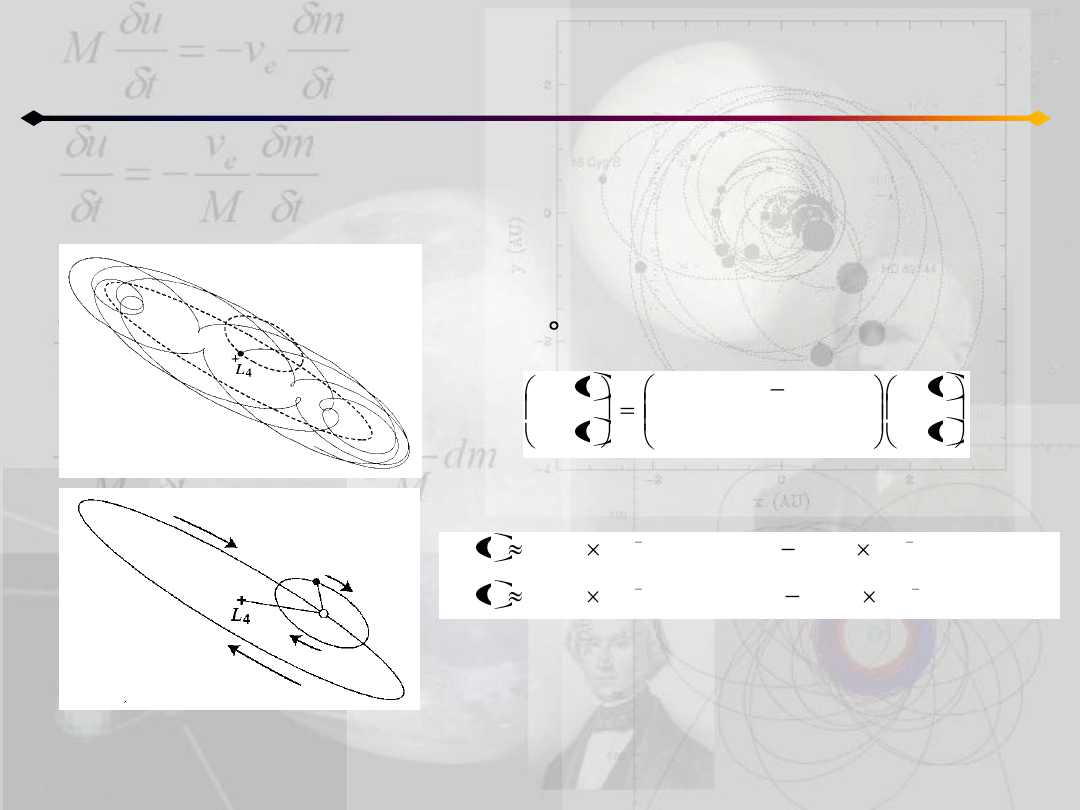
Ograniczone zagadnienie 3 ciał

Ruch w otoczeniu L

4

i L

5

Ze względu na nachylenie orbity w stosunku do
osi łączącej masy, można dokonad uproszczenia
zagadnienia przez obrót układu współrzędnych
o 30 :

Wtedy X(t) i Y(t) z przykładu przyjmują wartości:

Są to dwa ruchy po elipsie. Ruch przypomina
wcześniej analizowane przybliżenie „guiding
center”

t

Y

t

X

30

cos

30

sin

30

sin

30

cos

t

'

Y

t

'

X









t

963

.

0

cos

10

86

.

4

t

268

.

0

cos

10

23

.

6

t

'

Y

t

963

.

0

sin

10

85

.

9

t

268

.

0

sin

10

54

.

3

t

'

X

5

5

5

4

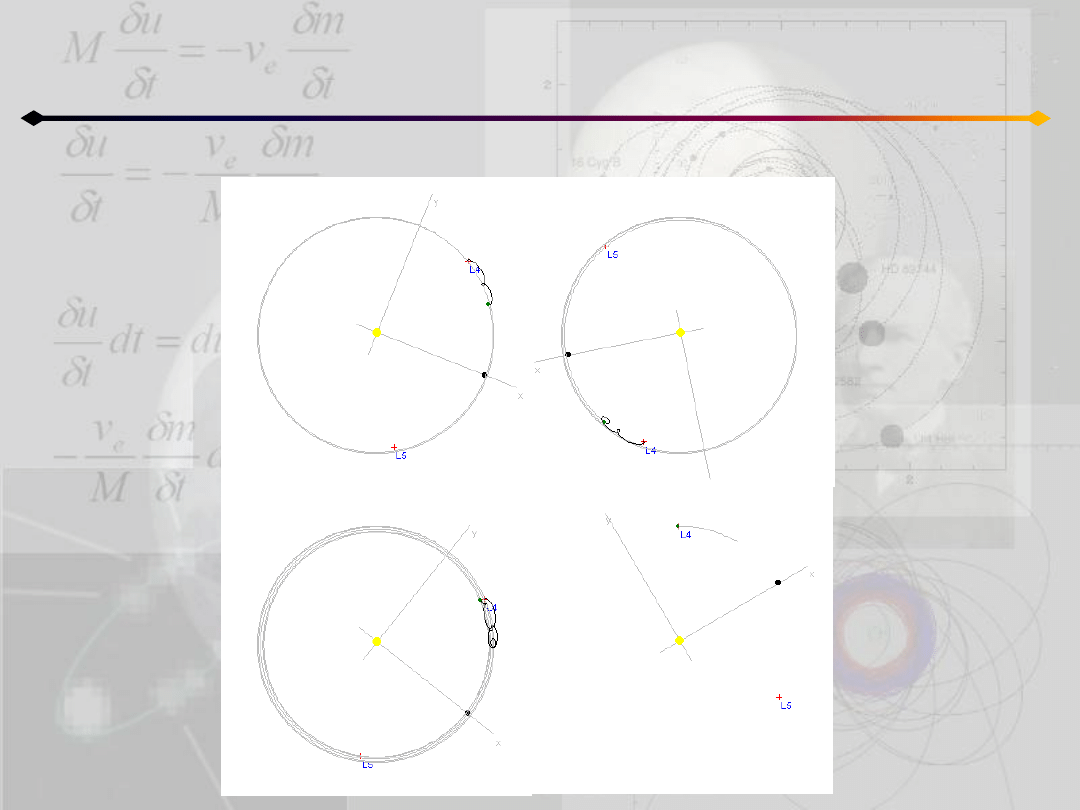
Ograniczone zagadnienie 3 ciał

Orbity typu kijanki (tadpole)

sajri.astronomy.cz

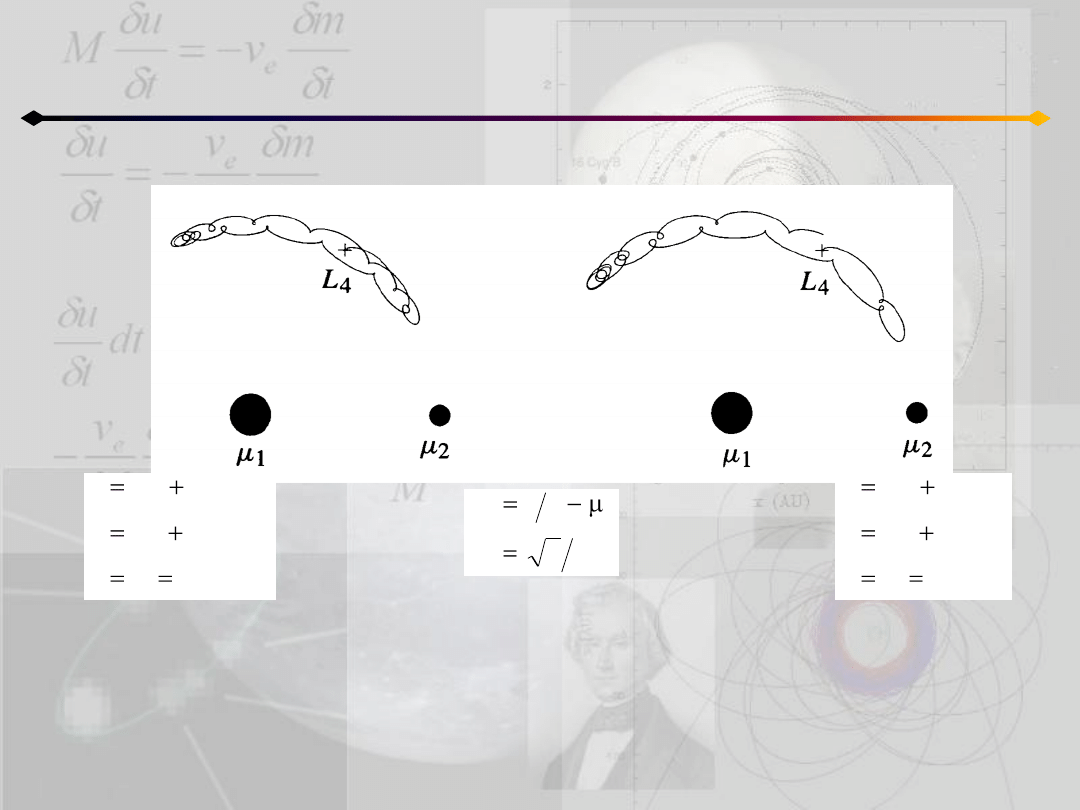
Ograniczone zagadnienie 3 ciał

Orbity typu kijanki (tadpole)

μ2=0.001 – podobnie jak w przypadku układu Słooce-Jowisz

Na prawym wykresie ruch cząstki rozpoczął się nieco dalej od punktu równowagi
Co się stanie jeżeli ruch rozpocznie się jeszcze dalej?

0

y

x

0065

.

0

y

y

0065

.

0

x

x

0

0





0

y

x

008

.

0

y

y

008

.

0

x

x

0

0





2

3

y

2

1

x

0

2

0

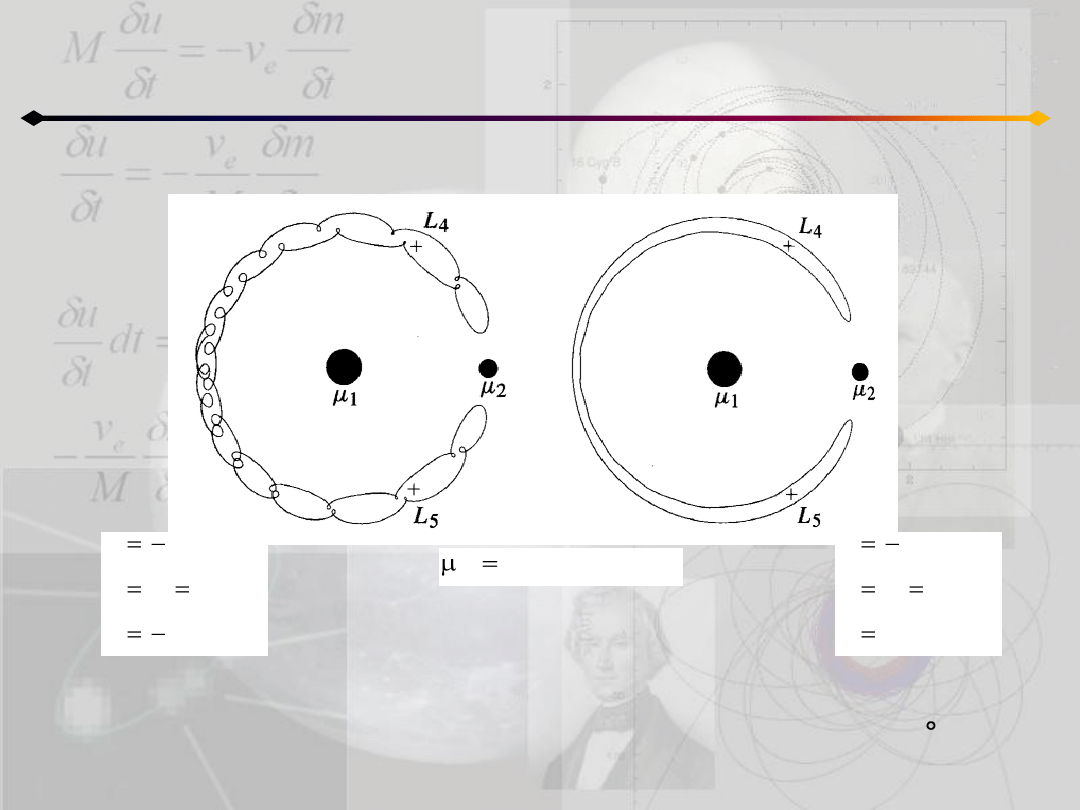
Ograniczone zagadnienie 3 ciał

Orbity typu podkowy (horseshoe)

Kąt jaki zakreśla cząstka może osiągnąd wartości dużo większe od 180

000953875

.

0

2

06118

.

0

y

0

x

y

97668

.

0

x





04032

.

0

y

0

x

y

02745

.

1

x





Ograniczone zagadnienie 3 ciał

Orbity typu podkowy (horseshoe)

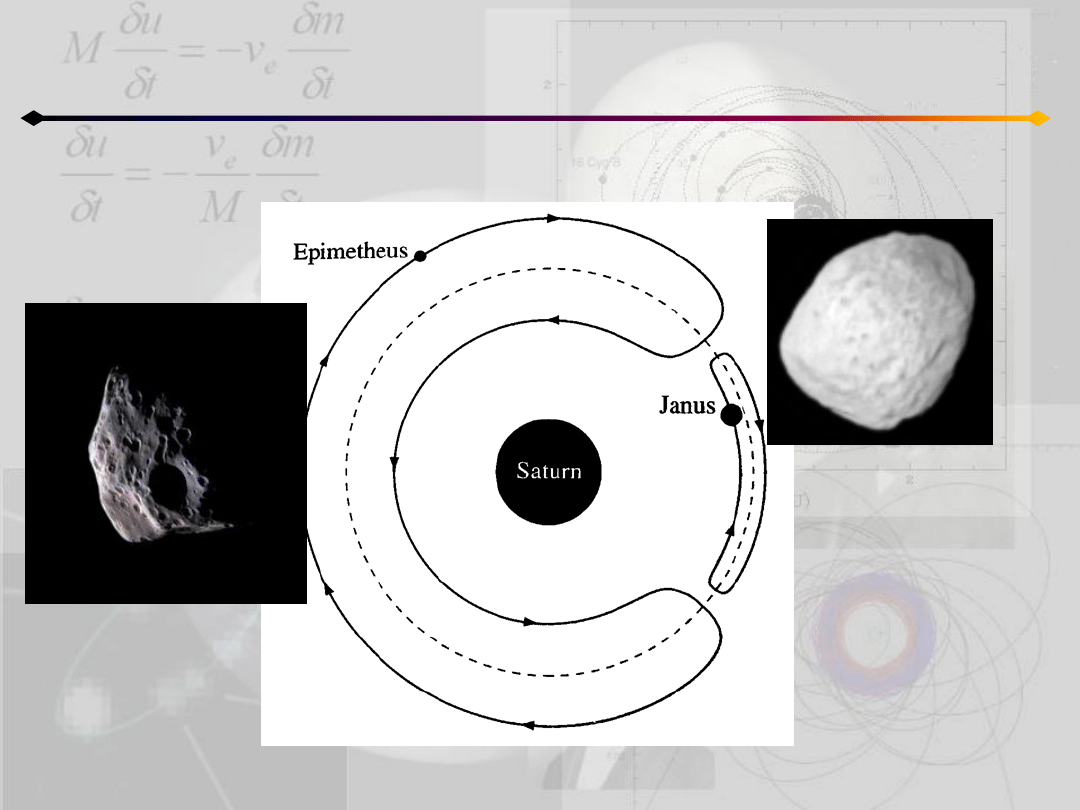
Ograniczone zagadnienie 3 ciał

Orbity typu kijanki (tadpole)

Janus

Prometeusz

Copyright by Calvin J. Hamilton

Ograniczone zagadnienie 3 ciał

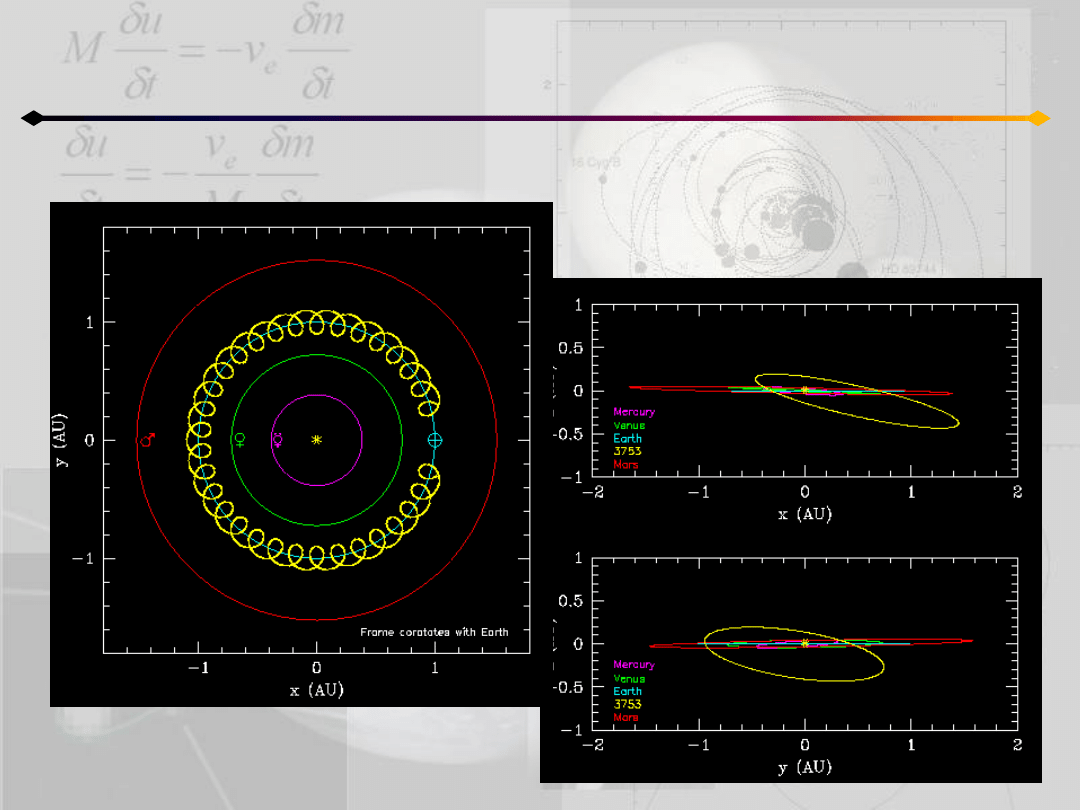
Orbity typu podkowy (horseshoe)

planetoida 2002 AA29
porusza się po orbicie
typu podkowy w układzie
Ziemia-Słooce

Copyright by Paul Wiegert

Ograniczone zagadnienie 3 ciał

Orbity typu podkowy (horseshoe)

planetoida 2002 AA29

Copyright by Paul Wiegert

Ograniczone zagadnienie 3 ciał

Orbity typu podkowy (horseshoe)

3753 Cruithine

Copyright by Paul Wiegert

Ograniczone zagadnienie 3 ciał

Quasi - księżyce

Copyright by Paul Wiegert

Tego rodzaju obiekty mogą zajmowad
stabilne orbity przez cały czas życia
Układu Słonecznego

Preferowane są dalsze planety –
quasi-księżyce znaleziono w przypadku
Urana i Neptuna

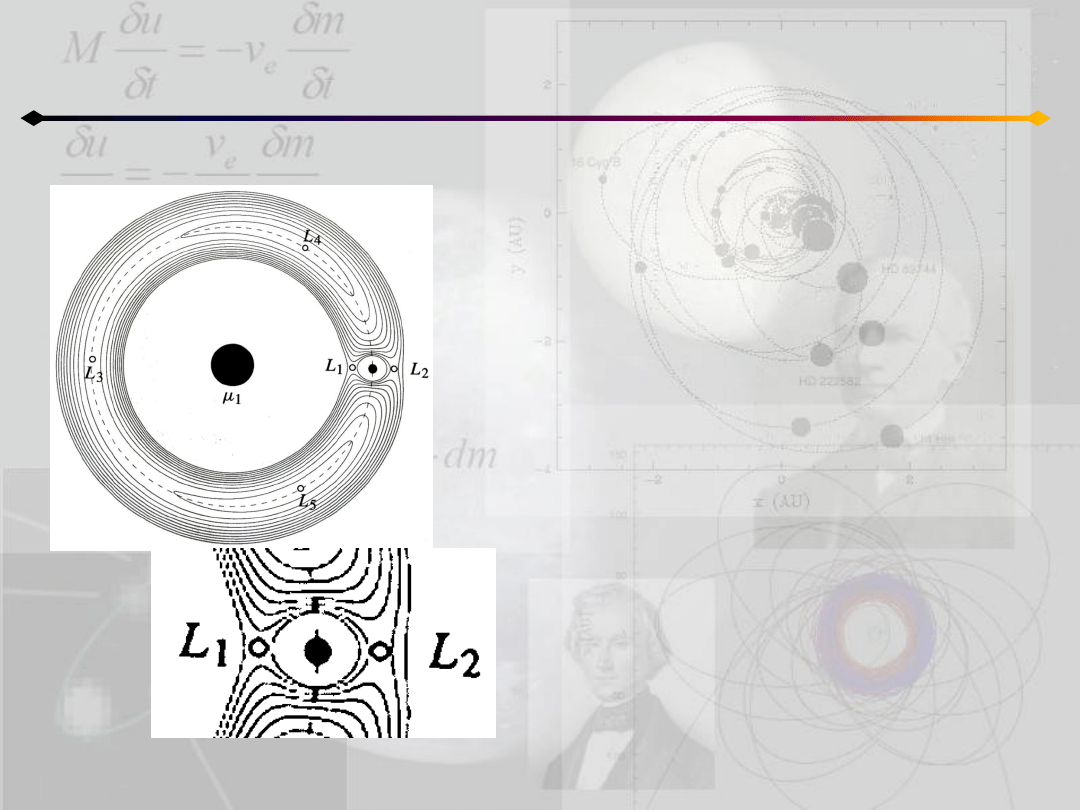
Ograniczone zagadnienie 3 ciał

Równania Hilla

Ruch cząstki wokół centralnej masy jest przez
większośd czasu keplerowski. Perturbacje
pojawiają się jedynie przy bliskim spotkaniu z
drugą masą.

Przykładem takiego ruchu są orbity typu podkowy
i kijanki.

Poza rozwiązywaniem pełnych równao ruchu warto
zbadad ruch wokół mniejszej masy.

Podstawy tego zagadnienia sformułował Hill (1878)

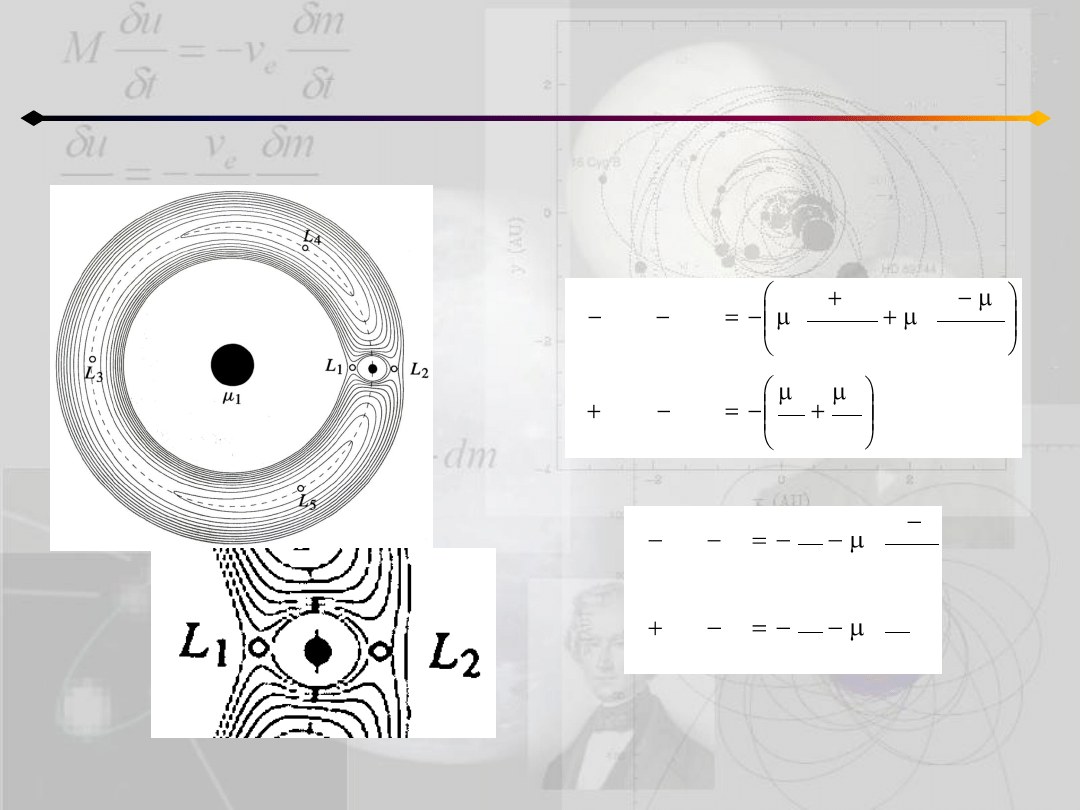
Ograniczone zagadnienie 3 ciał

Równania Hilla

y

r

r

y

n

x

n

2

y

r

x

r

x

x

x

n

y

n

2

x

3

2

2

3

1

1

2

3

2

1

2

3

1

2

1

2













Jeżeli różnica mas jest duża możemy przyjąd,
że μ

1

≈1, wtedy równania ruchu płaskiego:

przyjmują postad:

3

2

2

3

1

3

2

2

3

1

r

y

r

y

y

x

2

y

r

1

x

r

x

x

y

2

x













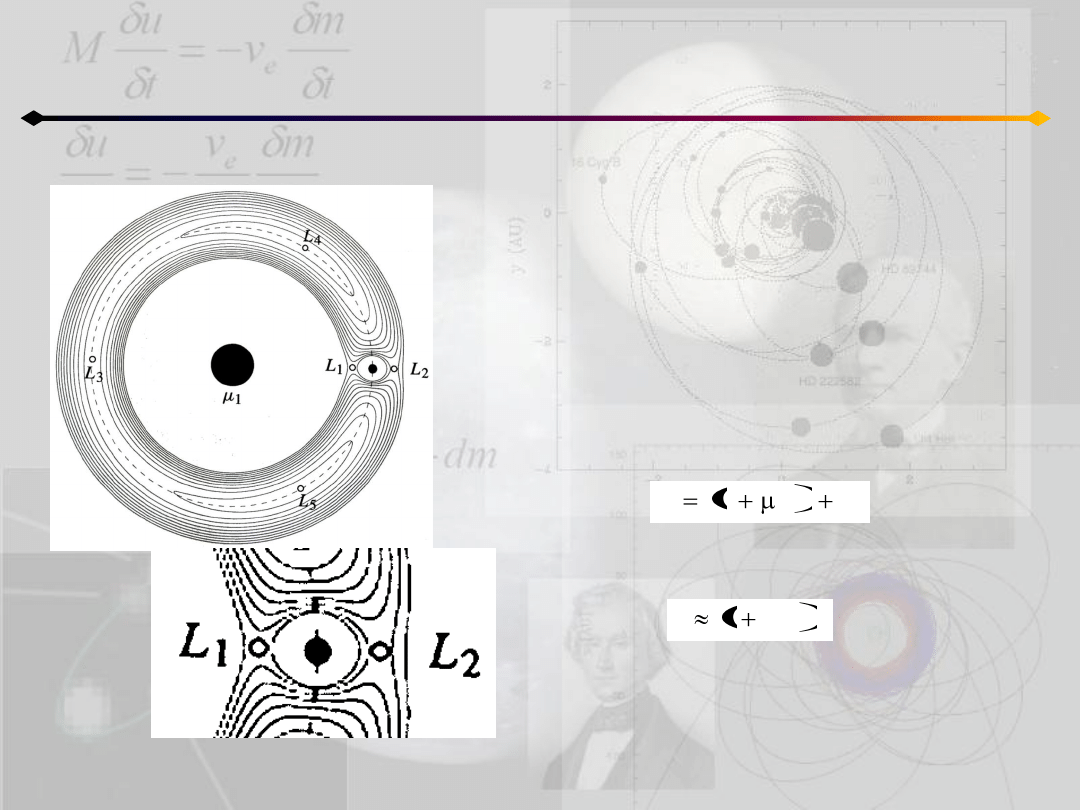
Ograniczone zagadnienie 3 ciał

Równania Hilla

W następnym kroku dokonujemy przesunięcia
początku układu współrzędnych tak, że x->1+x
i wprowadzamy Δ=r

2

.

Rozpatrujemy ruch w pobliżu masy m

2

(tzn. w

okolicy punktów L

1

i L

2

), więc x,y oraz Δ są

małymi wielkościami.

Rozwijając w szereg wyrażenie:

i zaniedbując wyższe potęgi μ

2

, dostajemy:

co pozwala przepisad równania ruchu w postaci:

2

2

2

2

1

y

x

r

2

/

1

1

x

2

1

r

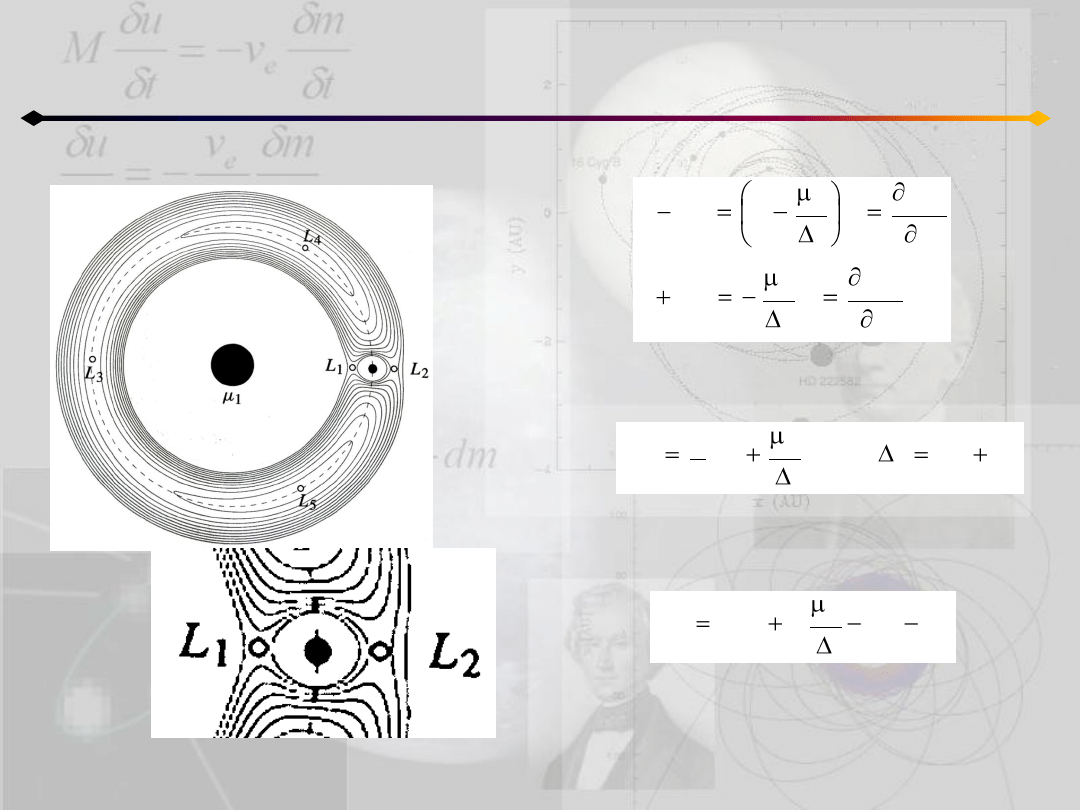
(14.1a)

(14.1b)

Są to tzw. równania Hilla, gdzie:

a zmodyfikowana stała Jacobiego jest równa:

(14.2)

Ograniczone zagadnienie 3 ciał

Równania Hilla

y

U

y

x

2

y

x

U

x

3

y

2

x

H

3

2

H

3

2













2

2

2

2

2

H

y

x

x

2

3

U

2

2

2

2

H

y

x

2

x

3

C





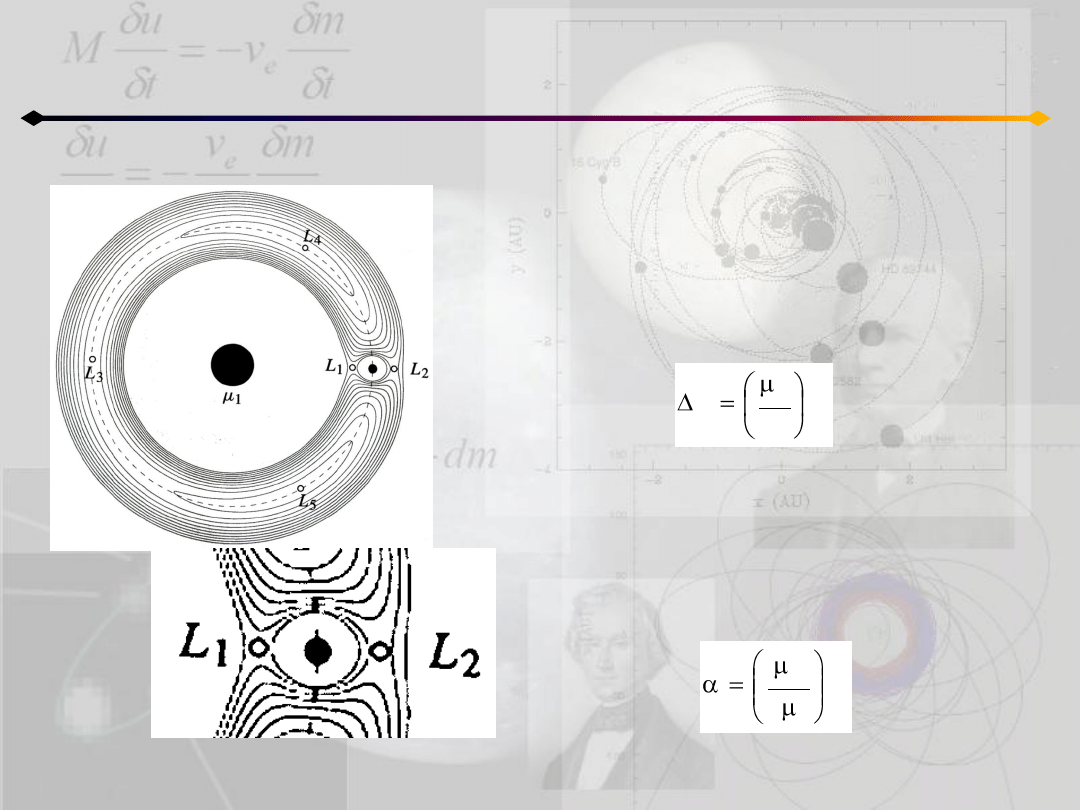
Ograniczone zagadnienie 3 ciał

Równania Hilla

Z równania 14.1a widzimy, że radialna składowa
siły znika kiedy 3Δ

3

=μ

2

.

To pozwala zdefiniowad sferę Hilla jako sferę
o promieniu:

otaczającą drugą masę.

Analogiczny wynik był uzyskany w przypadku
wyznaczania położeo punktów L

1

i L

2

(wykład 13):

3

/

1

2

H

3

3

/

1

1

2

3

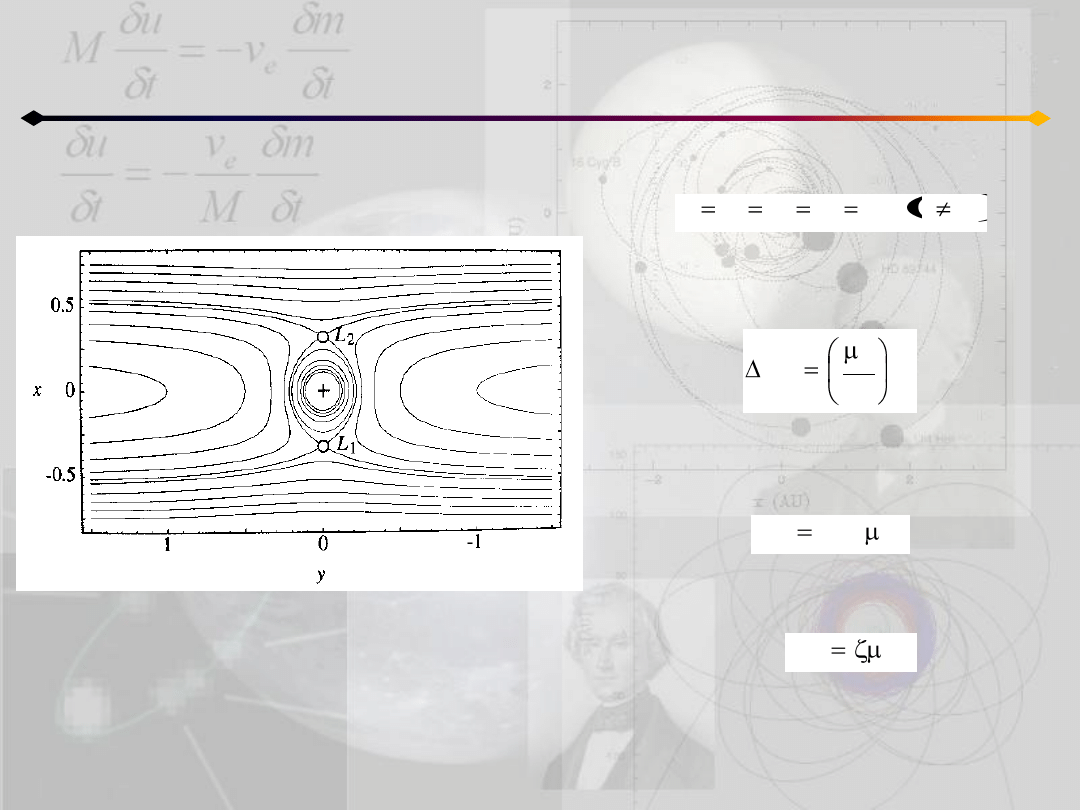
Ograniczone zagadnienie 3 ciał

Równania Hilla

Podstawiając w równaniach 14.1:

możemy znaleźd położenie punktów L

1

i L

2

.

Z równania 14.1a mamy:

a z równania 14.2 dostajemy odpowiednią
zmodyfikowaną stałą Jacobiego:

jeżeli zapiszemy:

(14.3)

to orbity typu podkowy są możliwe w
obszarze, w którym ζ<3

4/3

.

0

x

0

y

x

y

x













3

/

1

2

L

3

2

,

1

3

/

2

2

4

/

3

H

3

C

3

/

2

2

H

C

krzywe zerowej prędkości
w otoczeniu punktów L

1

i L

2

Ograniczone zagadnienie 3 ciał

Równania Hilla

Użyjemy teraz kryterium Tisseranda do wyznaczenia zależności między elementami
orbitalnymi przed i po spotkaniu z satelitą.

Niech elementy orbitalne przed i po spotkaniu z satelitą będą równe odpowiednio:

gdzie wszystkie wielkości oznaczone przez Δ są małe.

Z kryterium Tisseranda mamy:

co może byd rozwinięte do postaci:

lub:

2

2

2

1

1

1

e

e

a

1

a

e

e

a

1

a

const

e

1

a

1

2

a

1

1

2

/

1

2

2

/

1

const

e

a

4

3

2

2

2

2

2

2

2

1

2

1

e

a

4

3

e

a

4

3

const

I

cos

e

1

a

a

2

1

2

Ograniczone zagadnienie 3 ciał

Równania Hilla

Tą samą zależnośd można uzyskad z równao Hilla:

w przypadku dużych wartości Δ:

co może byd zapisane jako (przy użyciu 14.2 i 14.3):

Używając teraz przybliżenia „guiding centre” możemy zapisad (n=1):

wtedy z równao 14.4:

y

x

2

y

x

3

y

2

x

3

2

3

2













0

x

2

y

x

3

y

2

x













3

/

2

2

2

2

2

x

3

y

x





t

sin

e

x

t

cos

e

x

t

sin

e

a

x







t

cos

e

2

y

t

sin

e

2

a

2

3

y







(14.4)

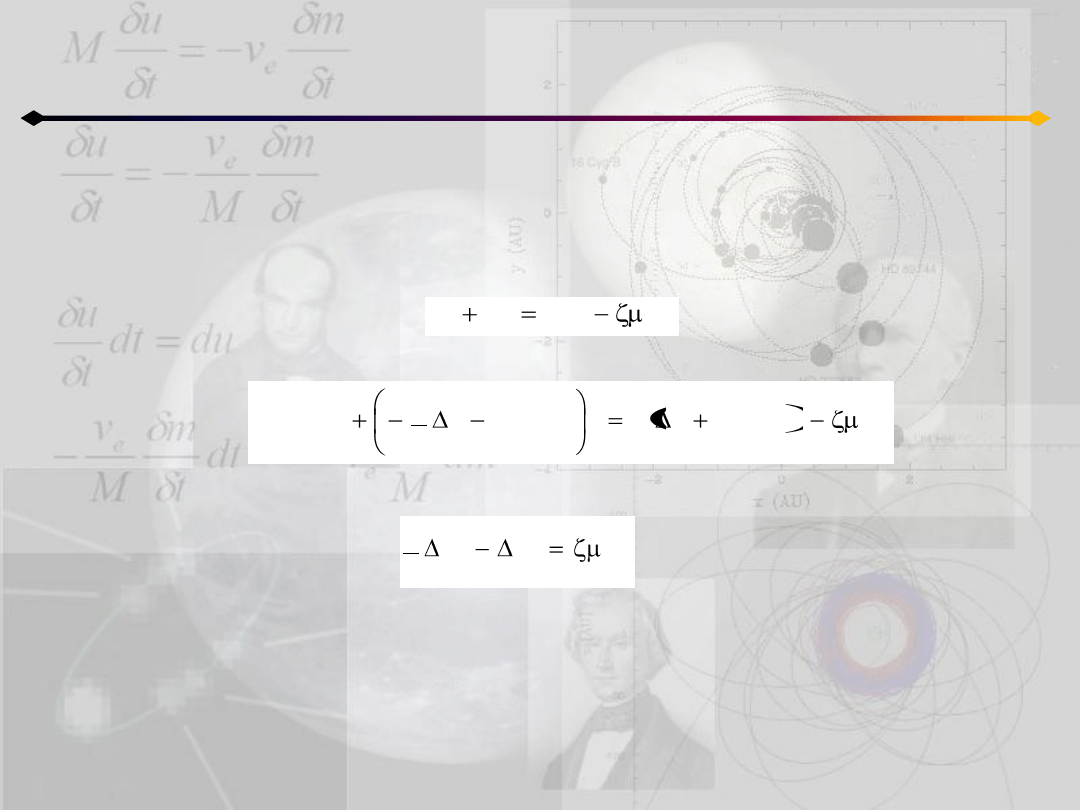
Ograniczone zagadnienie 3 ciał

Równania Hilla

Uzyskane wyrażenia można użyd do przekształcenia równania:

do postaci:

z którego mamy:

gdzie prawa strona jest stała.

3

/

2

2

2

2

2

x

3

y

x





3

/

2

2

2

2

2

2

t

sin

e

a

3

t

sin

e

2

a

2

3

t

cos

e

3

/

2

2

2

2

e

a

4

3

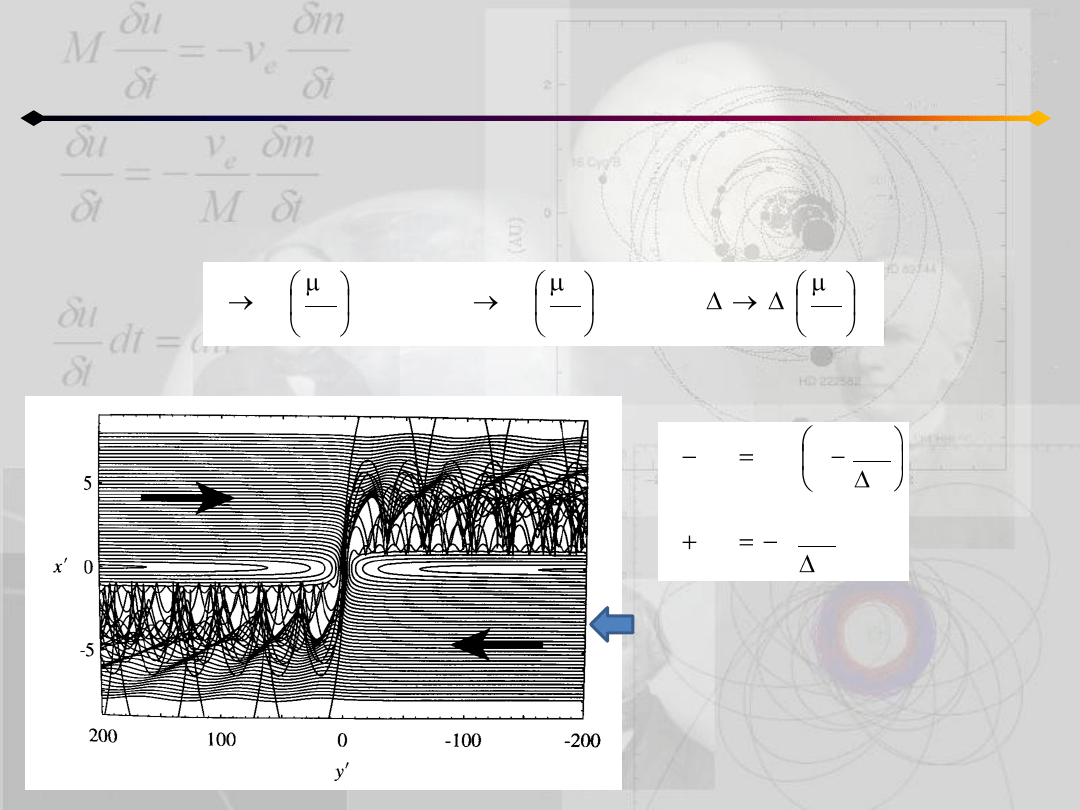
Ograniczone zagadnienie 3 ciał

Równania Hilla

Równania Hilla skalują się z μ

2

1/3

. Jeśli podstawimy:

to równania ruchu 14.1 przyjmują postad:

Trajektorie cząstki otrzymane ze
skalowalnej postaci równao Hilla.
Masa perturbująca jest w początku
układu

3

/

1

2

3

/

1

2

3

/

1

2

3

'

3

'

y

y

3

'

x

x

3

3

'

'

y

3

'

x

2

'

y

'

1

1

'

x

3

'

y

2

'

x













Ograniczone zagadnienie 3 ciał

Księżyce „pasterskie”

www.astro.ljmu.ac.uk

www.universetoday.com

Ograniczone zagadnienie 3 ciał

Księżyce „pasterskie”

Copyright of Cassini Team