MECHANIKA NIEBA

WYKŁAD 6

09.04.2008 r

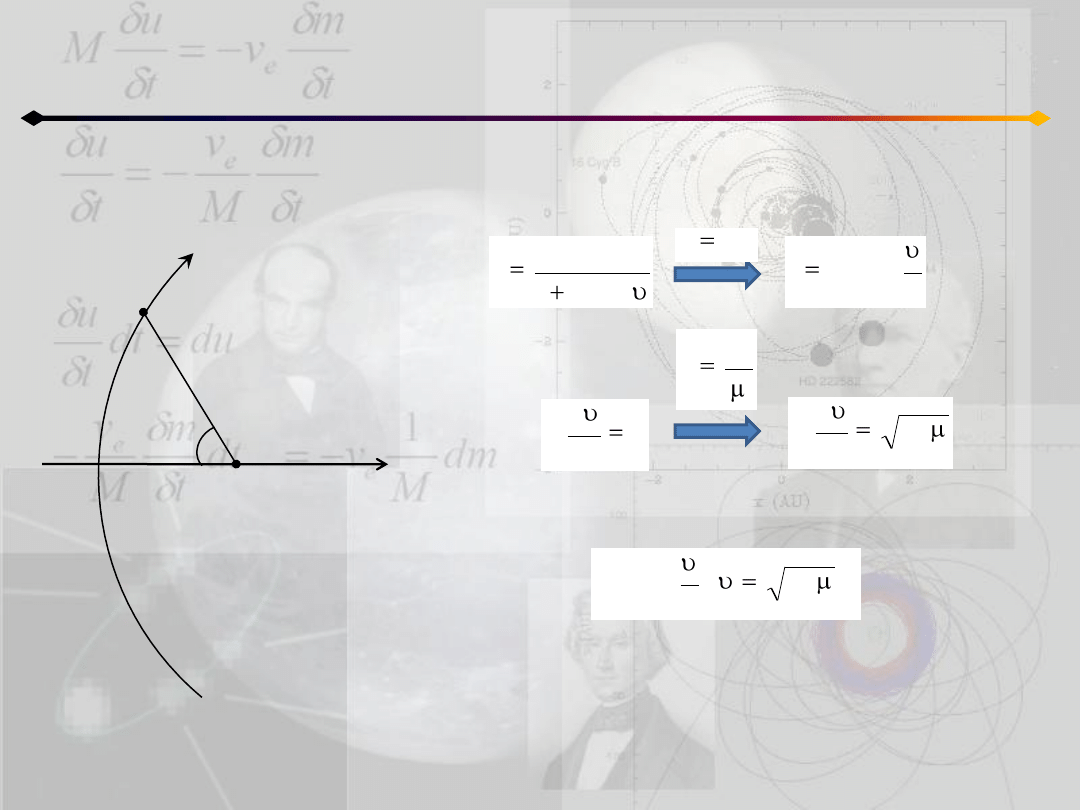
Położenie punktu na orbicie

h=0 (uzupełnienie)

Π

r

P

O

q

υ

cos

e

1

p

r

h=0 oznacza ruch po paraboli (e=1):

całka pól:

łącząc powyższe równania otrzymujemy:

q

2

p

2

sec

q

r

2

c

dt

d

r

2

2

c

p

q

2

dt

d

r

2

dt

q

2

d

2

sec

q

4

2

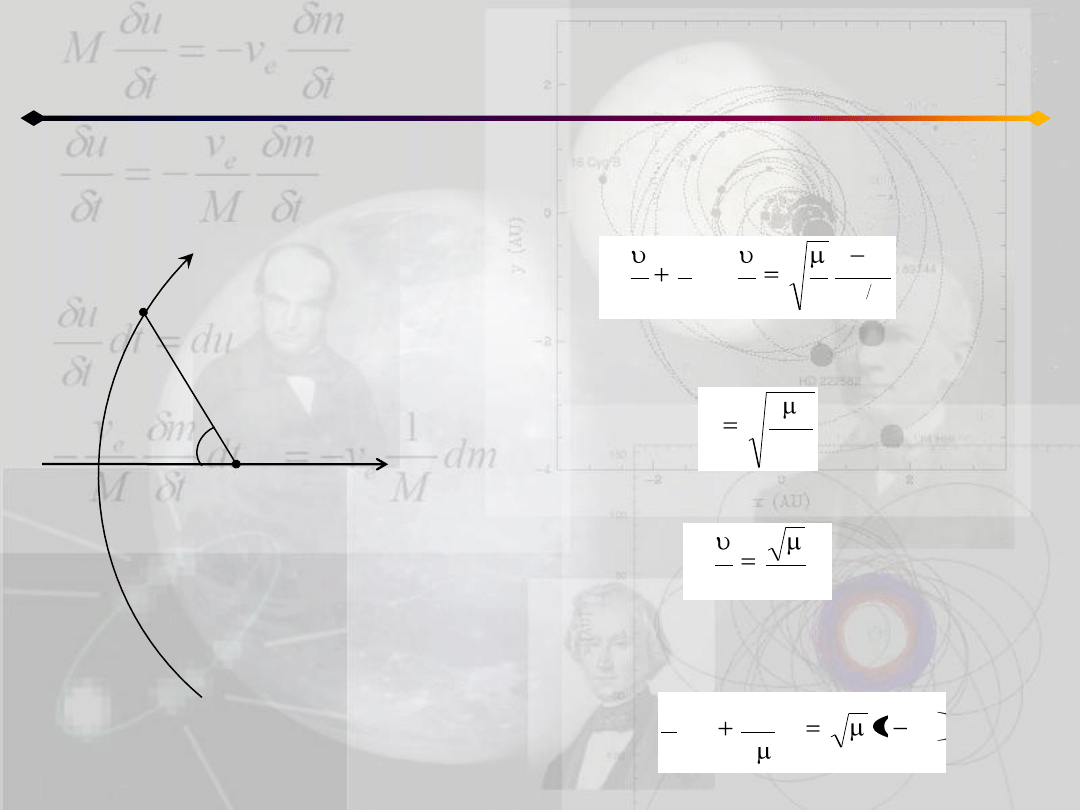
Położenie punktu na orbicie

h=0 (uzupełnienie)

Π

r

P

O

q

υ

Całkując otrzymane równanie dostajemy 
równanie Barkera:

oznaczając ruch średni:

i wykorzystując uzyskaną wcześniej zależnośd:

można przepisad równanie Barkera w postaci:

2

3

3

q

T

t

2

2

tg

3

1

2

tg

3

q

2

n

E

c

2

tg

T

t

E

2

c

E

6

1

2

3

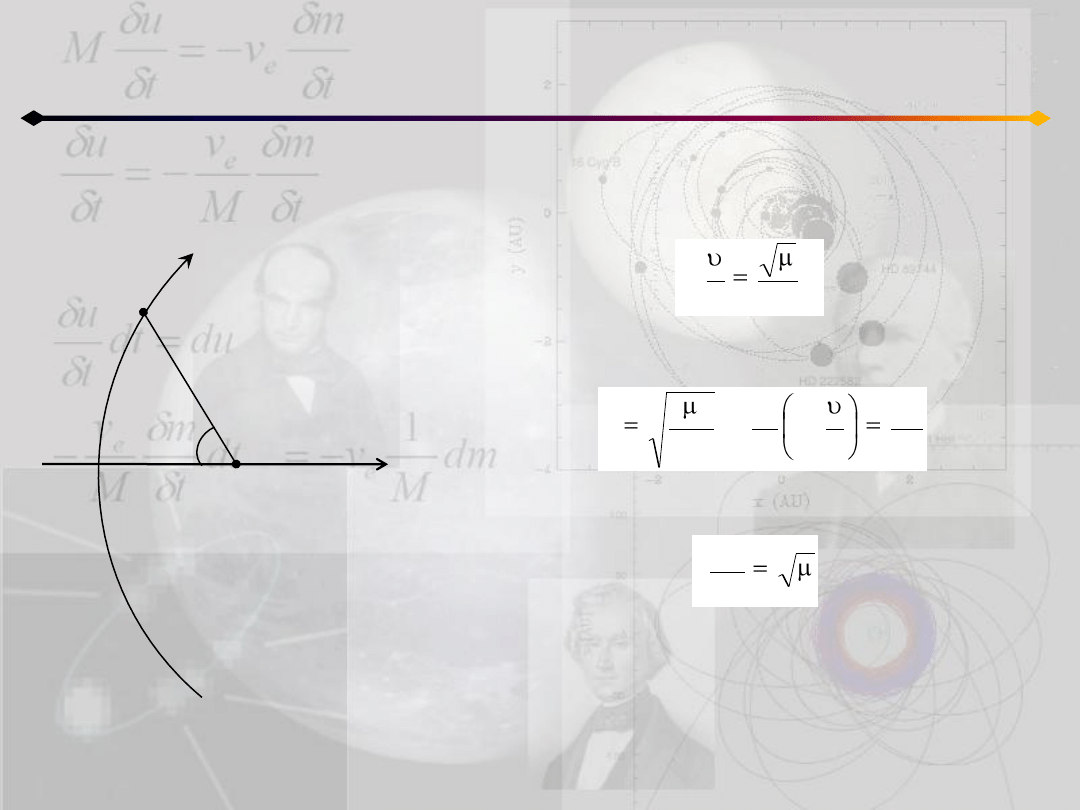
Położenie punktu na orbicie

h=0 (uzupełnienie)

Π

r

P

O

q

υ

Różniczkując wyrażenie:

i uwzględniając uzyskane wcześniej:

otrzymujemy:

które uzasadnia wcześniejszy wybór stałej k

r

nq

2

tg

dt

d

;

q

2

n

3

E

c

2

tg

dt

dE

r

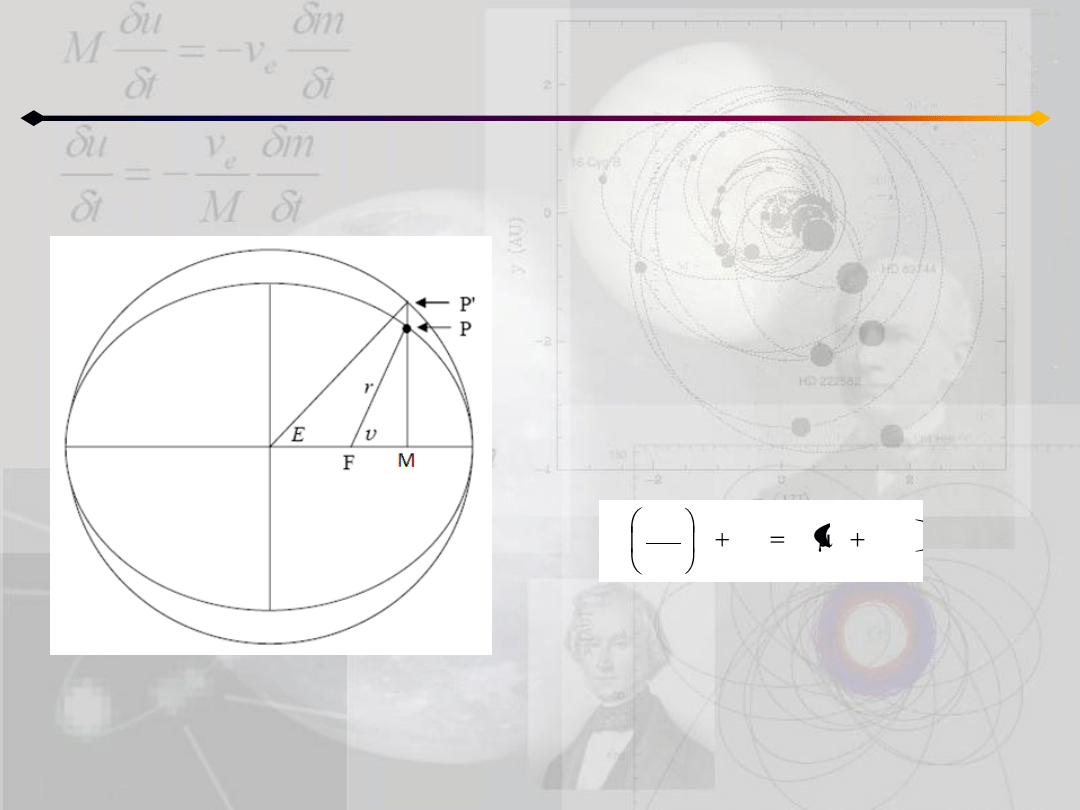
Położenie punktu na orbicie

h≠0

O

W tym wypadku mamy trzy możliwe rodzaje 
ruchu:

a) liniowy – c=0 
b) hiperboliczny – c≠0, h>0
c) eliptyczny – c≠0, h<0

Rozpatrzmy równanie (5.5):

h

r

r

2

c

dE

dr

k

2

2

2

2

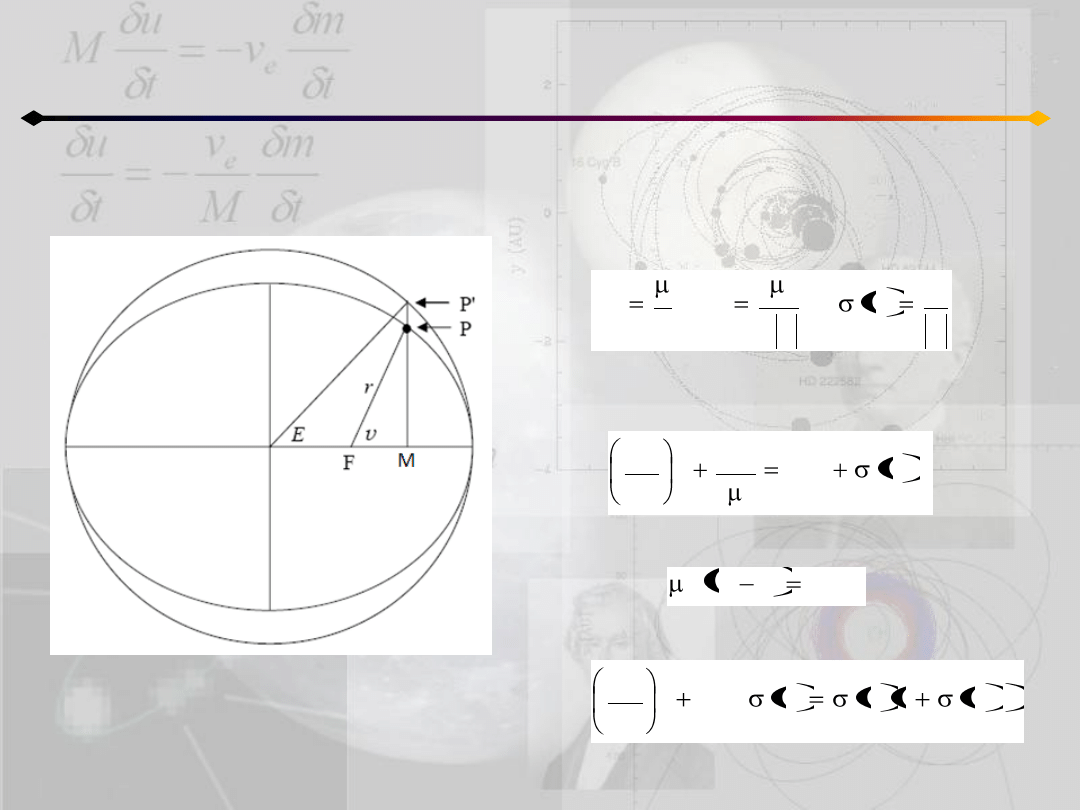
Położenie punktu na orbicie

h≠0

O

oznaczając:

h

h

h

;

h

2

a

;

a

k

2

możemy przekształcid do postaci:

2

2

2

r

h

ar

2

ac

dE

dr

a następnie korzystając z relacji (5.3):

uzyskujemy:

2

2

2

hc

2

1

e

2

2

2

2

r

h

a

h

h

e

a

dE

dr

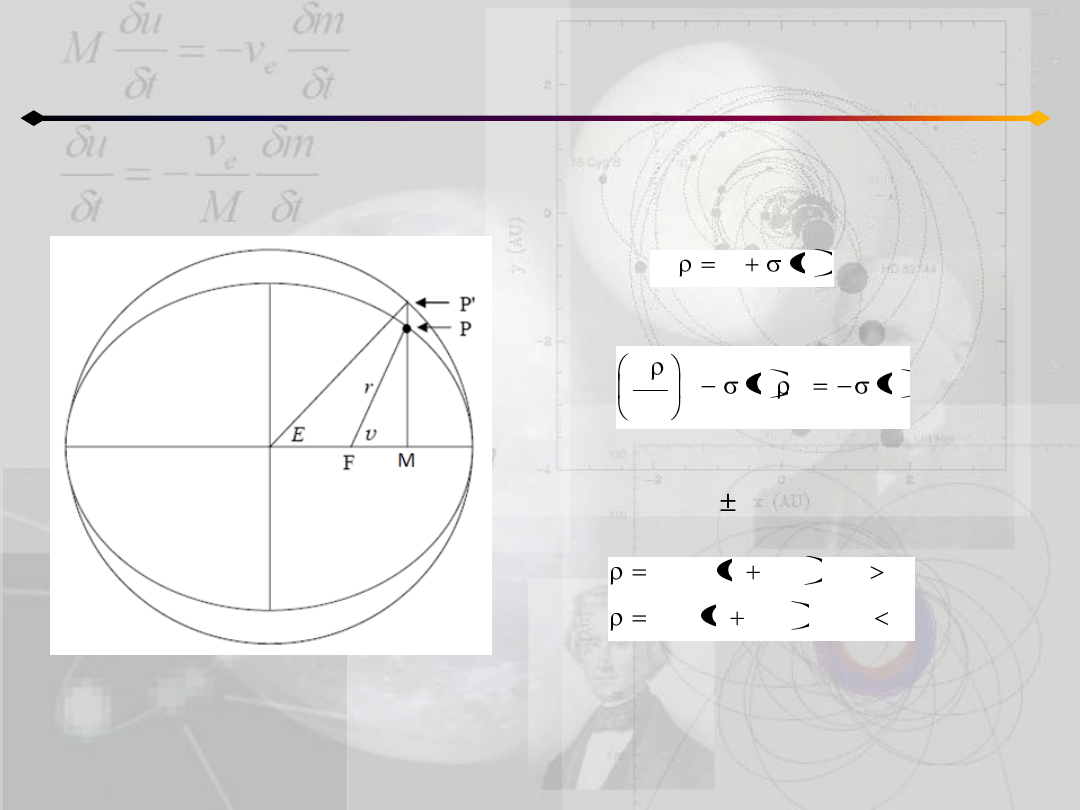
Położenie punktu na orbicie

h≠0

O

definiując nową zmienną ρ(E):

otrzymujemy:

r

h

a

ea

h

h

dE

d

2

2

Rozwiązaniami takiego równania są (poza 
przypadkami ρ= 1):

0

h

,

K

E

cos

0

h

,

K

E

cosh

2

1

(5.6)

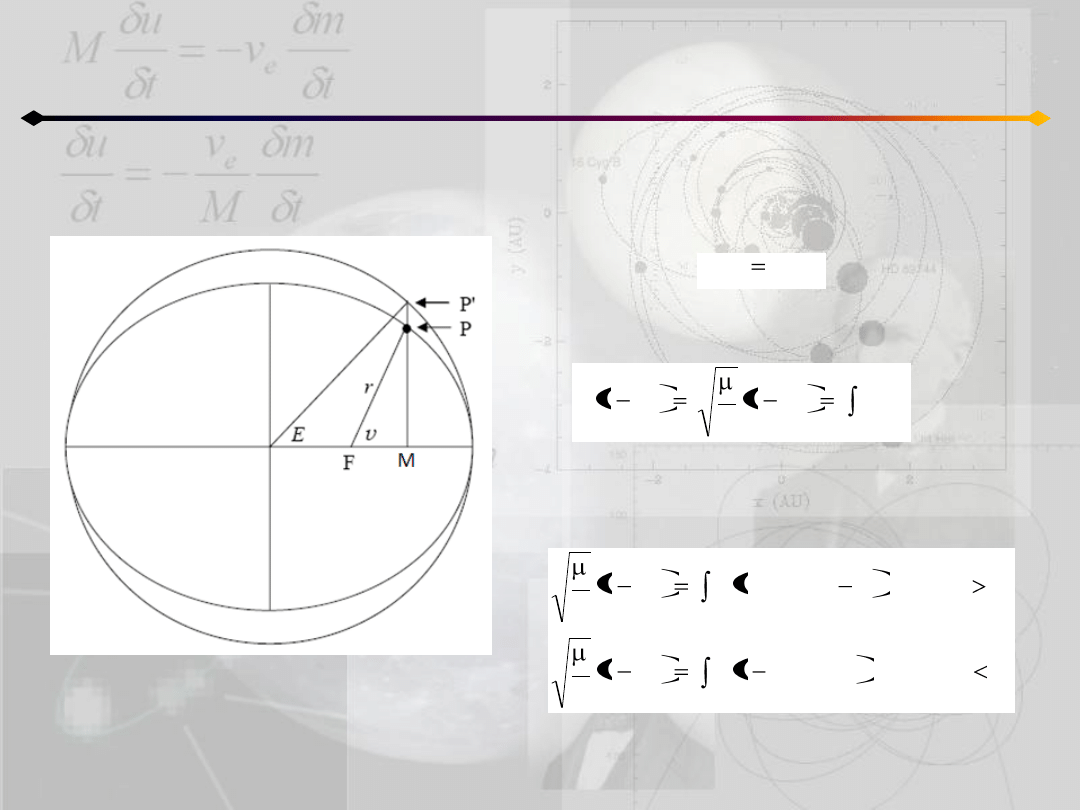
Położenie punktu na orbicie

h≠0

O

Podobnie jak to było robione dla przypadku
h=0, z całkowania równania:

dostajemy:

dE

r

dt

k

dE

r

T

t

a

T

t

k

E

0

Używając tego w równaniach (5.6):

0

h

,

dE

E

cos

e

1

a

T

t

a

0

h

,

dE

1

E

cosh

e

a

T

t

a

E

0

E

0

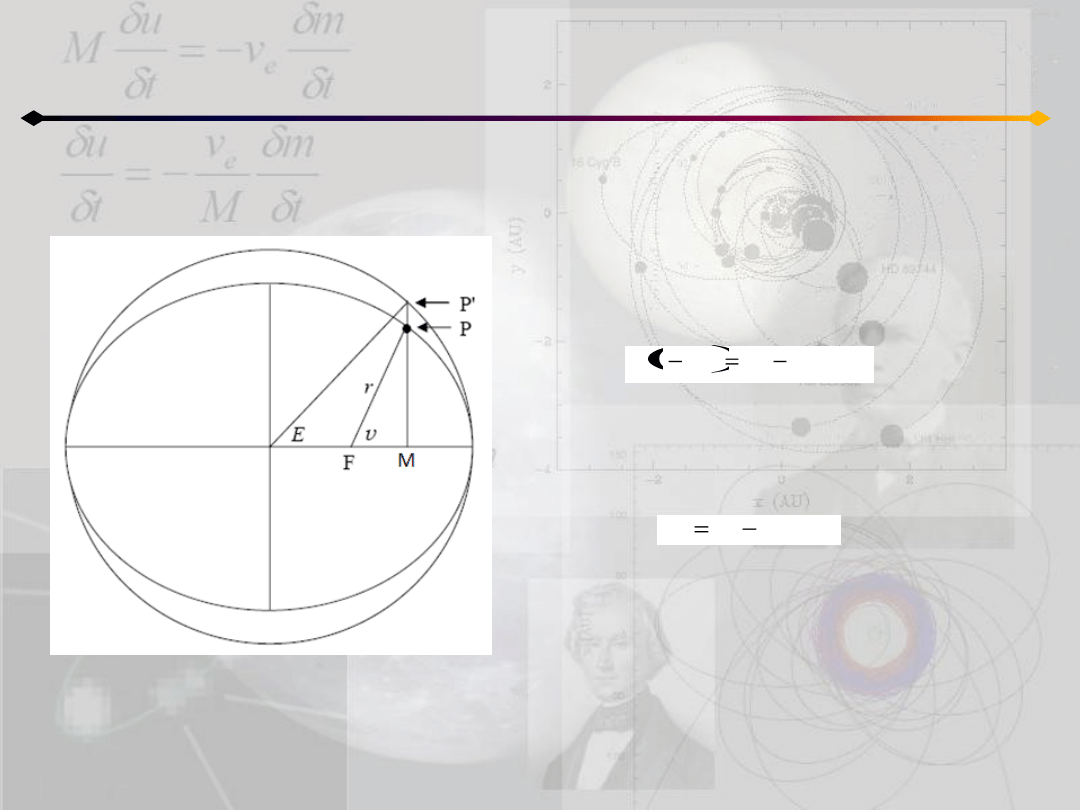
Położenie punktu na orbicie

h<0

O

Drugie z otrzymanych równao odpowiada
przypadkowi orbity eliptycznej. 

Uwzględniając trzecie prawo Keplera możemy
je przekształcid do postaci:

E

sin

e

E

T

t

n

Wprowadzając anomalię średnią M dostajemy 
ostatecznie równanie Keplera:

które pozwala otrzymad T – czas przejścia przez 
perycentrum w ruchu eliptycznym 

Postępując podobnie otrzymamy analogiczne 
równanie dla hiperboli.

E

sin

e

E

M

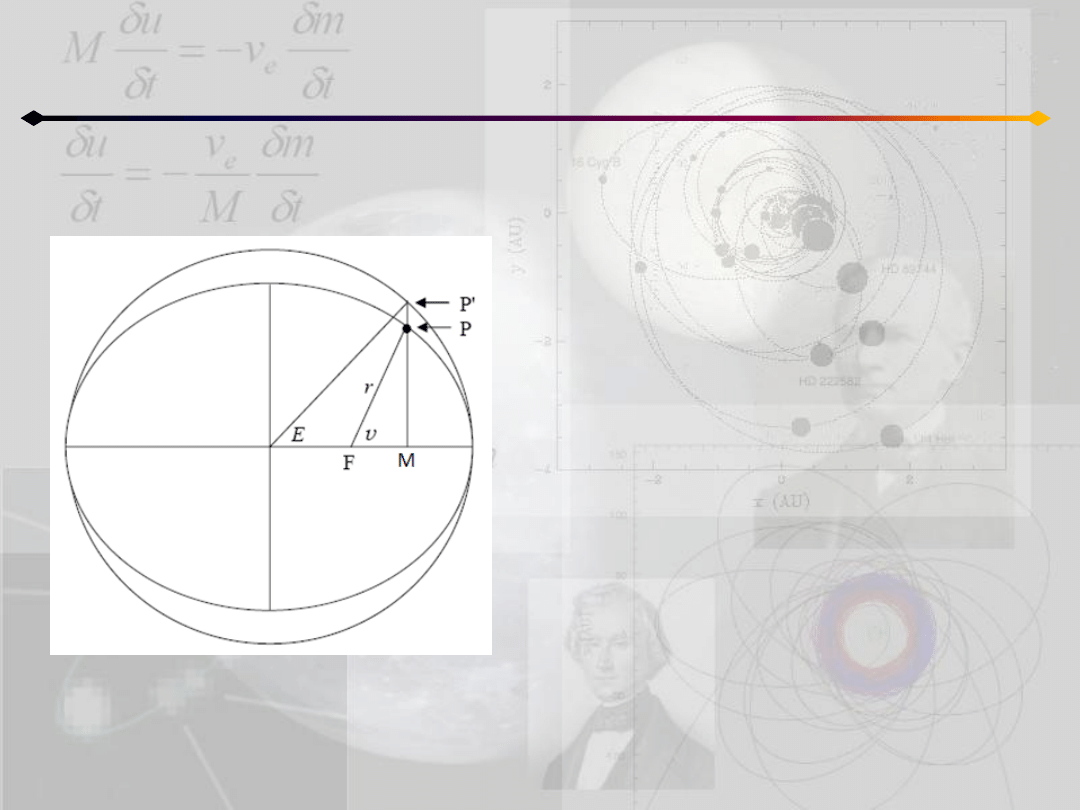
Położenie punktu na orbicie

h<0

O

Równanie Keplera ma prostą postad, ale nie 
istnieje jego dokładne rozwiązanie.

Jego przybliżone rozwiązania można podzielid 
na dwie grupy:

a) analityczne – z własności funkcji 
sinus dokonuje się rozwinięcia w 
szereg
b) numeryczne – wykorzystując różne 
metody rozwiązywania równao 
nieliniowych otrzymuje się przybliżenia
o różnym stopniu zbieżności i 
dokładności

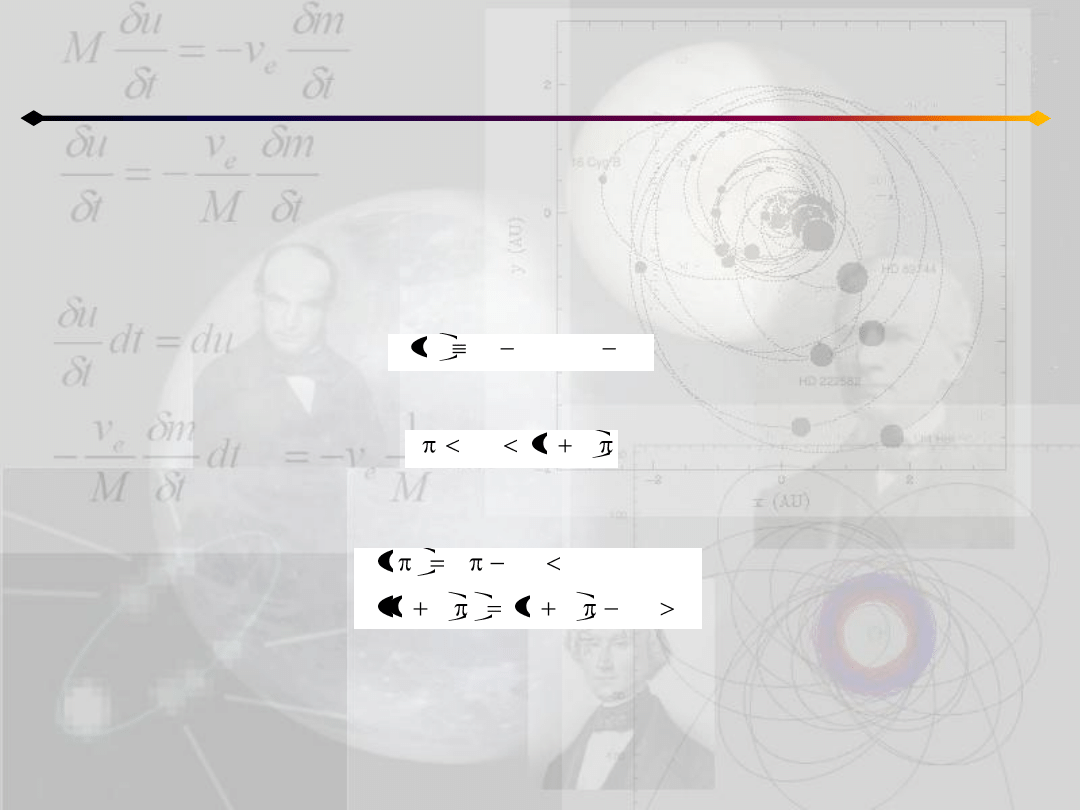
Położenie punktu na orbicie

Rozwiązanie równania Keplera

Na początku należałoby pokazad, że to równanie ma jedno i tylko jedno rozwiązanie.

W tym celu rozpatrzymy funkcję:

oraz załóżmy:

M

E

sin

e

E

E

F

1

n

M

n

W takim razie:

Funkcja F(E) ma co najmniej jeden pierwiastek w rozpatrywanym przedziale

0

M

1

n

1

n

F

0

M

n

n

F

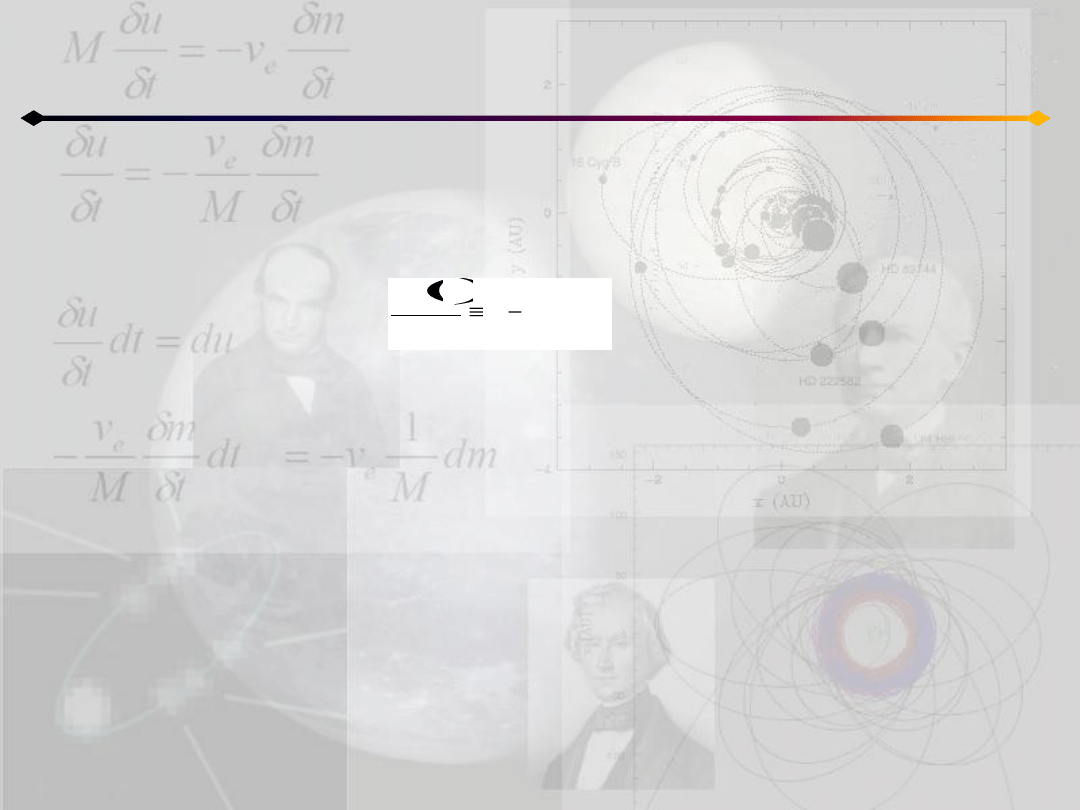
Położenie punktu na orbicie

Rozwiązanie równania Keplera

Zróżniczkujmy funkcję F(E):

iloczyn ecosE jest mniejszy od 1 (mamy do czynienia z elipsą), czyli funkcja jest 
rosnąca w całym przedziale.

Wnioskujemy stąd, że mamy tylko jeden pierwiastek w przedziale (nπ,(n+1)π).

E

cos

e

1

dE

E

dF

Następnym krokiem w rozwiązaniu równania Keplera jest znalezienie zerowego 
przybliżenia rozwiązania.

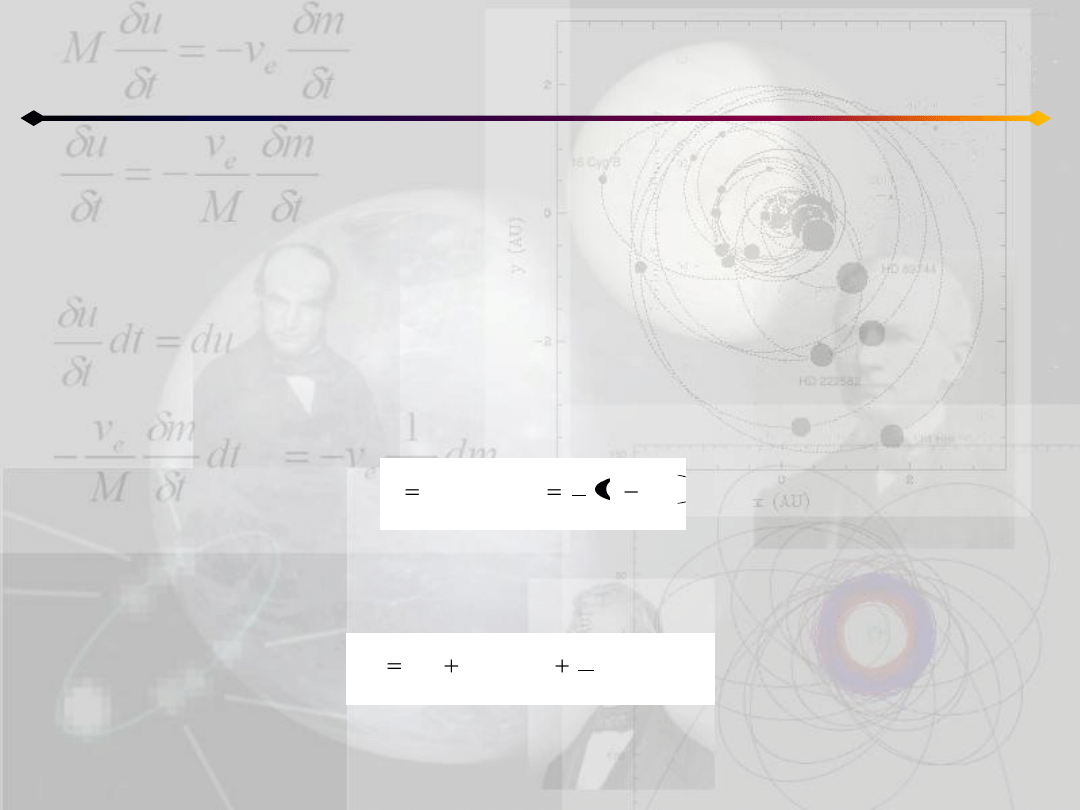
Położenie punktu na orbicie

Rozwiązanie równania Keplera

Zerowe przybliżenie może byd liczone na wiele różnych sposobów.

1. Jeśli mamy kilka wyznaczonych wartości E dla kilku dat to następną otrzymujemy 

poprzez ekstrapolację.

2. Można skorzystad z jednej z wielu metod graficznych, np.:

3. Znając M i e możemy także skorzystad z rozwinięcia w szereg:

rysujemy w jednym układzie współrzędnych dwie krzywe:

i znajdujemy E, dla którego przecinają się

M

E

e

1

y

;

E

sin

y

M

2

sin

e

2

1

M

sin

e

M

E

2

0

Położenie punktu na orbicie

Rozwiązanie równania Keplera

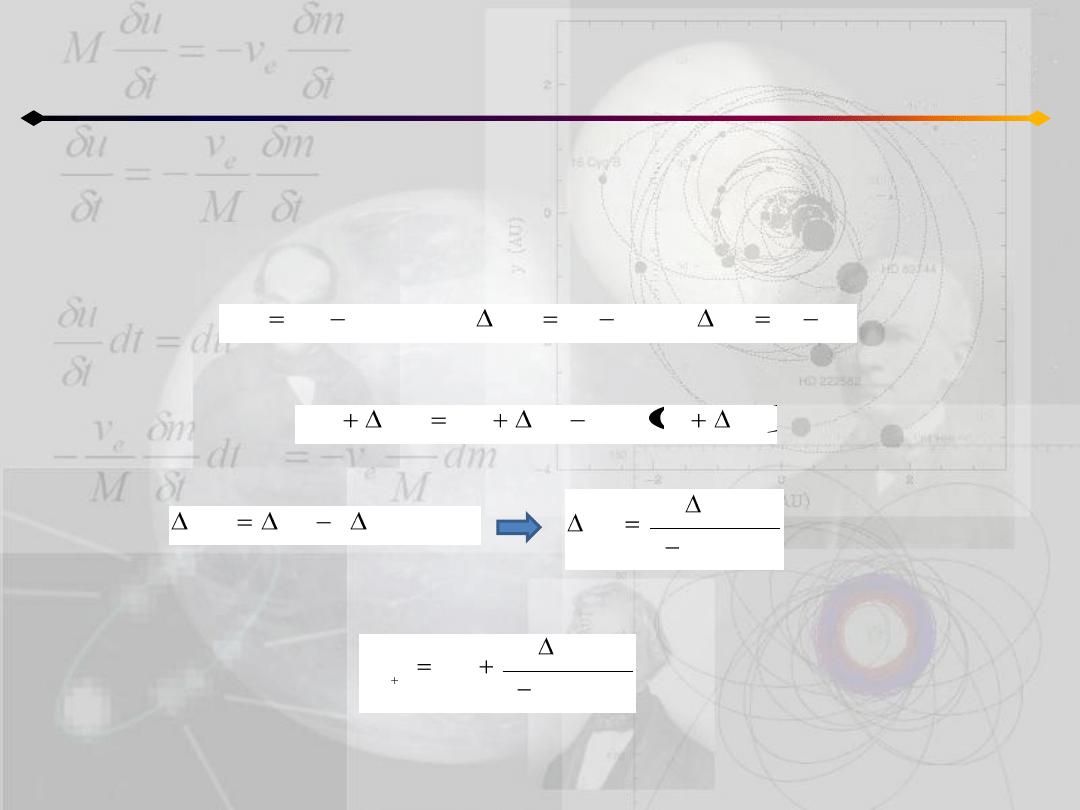
Znalezione zerowe przybliżenie, E

0

może zostad uściślone w następujący sposób. 

Mamy:

gdzie E jest dokładną wartością. Chcemy znaleźd ΔE

0

. Z równania Keplera:

ponieważ ΔE

0

jest bardzo małe więc:

następnie powtarzamy procedurę aż do uzyskania założonej dokładności.

0

0

0

0

0

0

0

E

E

E

;

M

M

M

;

E

sin

e

E

M

0

0

0

0

0

0

E

E

sin

e

E

E

M

M

0

0

0

0

E

cos

E

e

E

M

0

0

0

E

cos

e

1

M

E

k

k

k

1

k

E

cos

e

1

M

E

E

Położenie punktu na orbicie

Rozwiązanie równania Keplera

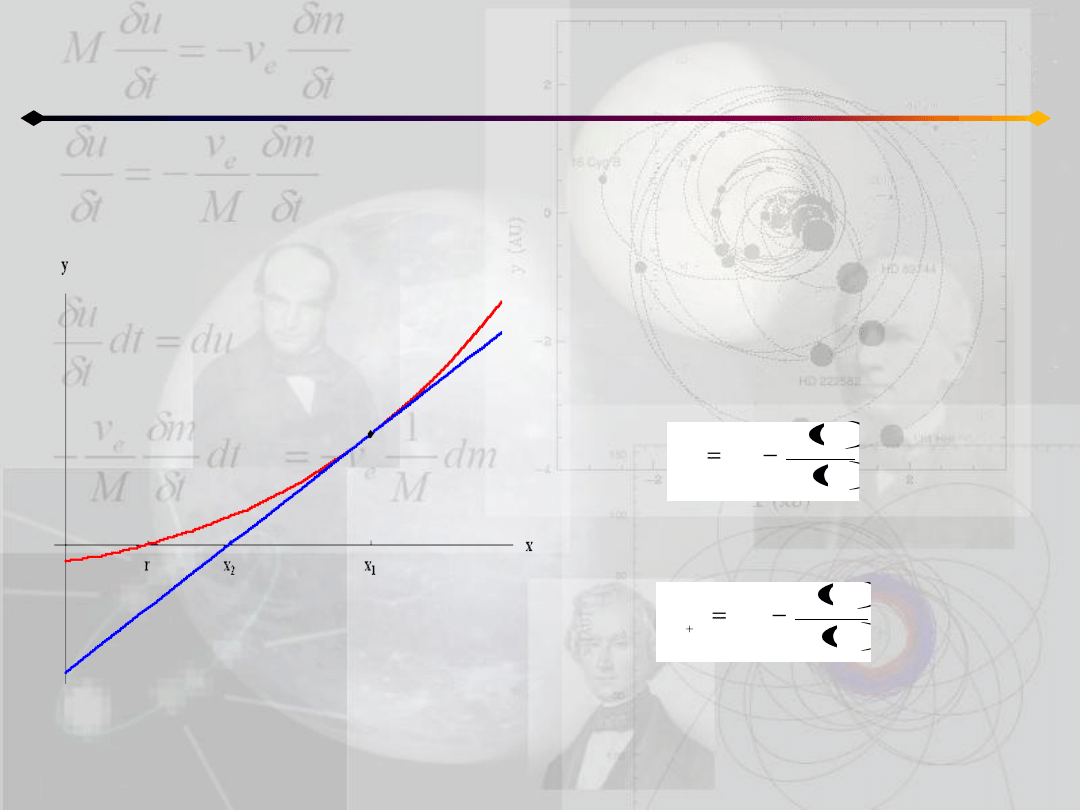
(metoda Newtona-Raphsona)

Metoda N-R pozwala znaleźd miejsce zerowe
funkcji f(x).

Liczymy jej pochodną w punkcie x

1

, przy 

czym f’(x

1

)≠0.

znajdujemy x

2

:

wzór ogólny: 

pozwala wyznaczyd miejsce zerowe z zadaną 
dokładnością

1

1

1

2

x

'

f

x

f

x

x

n

n

n

1

n

x

'

f

x

f

x

x

Położenie punktu na orbicie

Rozwiązanie równania Keplera

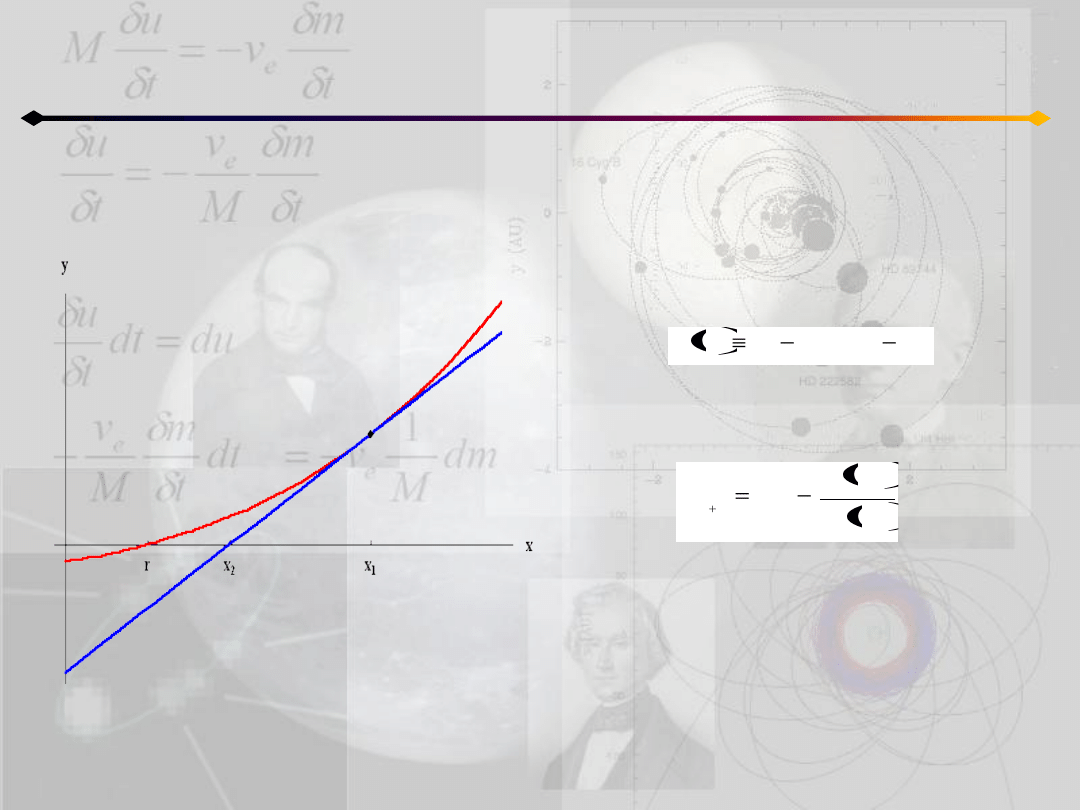
(metoda Newtona-Raphsona)

Metoda N-R dla równania Keplera:

daje wzór ogólny postaci:

M

E

sin

e

E

E

F

n

n

n

1

n

E

'

f

E

f

E

E

Położenie punktu na orbicie

h<0

O

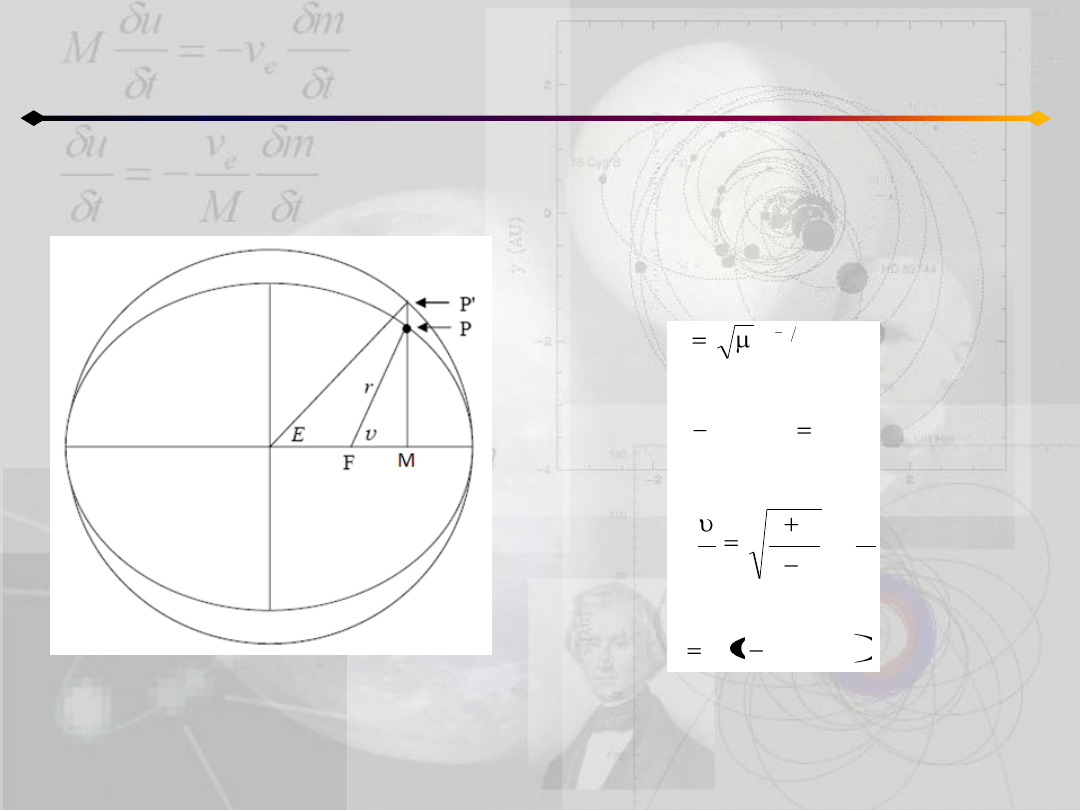
Do wyznaczenia położenia ciała na orbicie 
eliptycznej otrzymaliśmy następujący zestaw
równao:

E

cos

e

1

a

r

2

E

tg

e

1

e

1

2

tg

M

E

sin

e

E

a

n

2

3

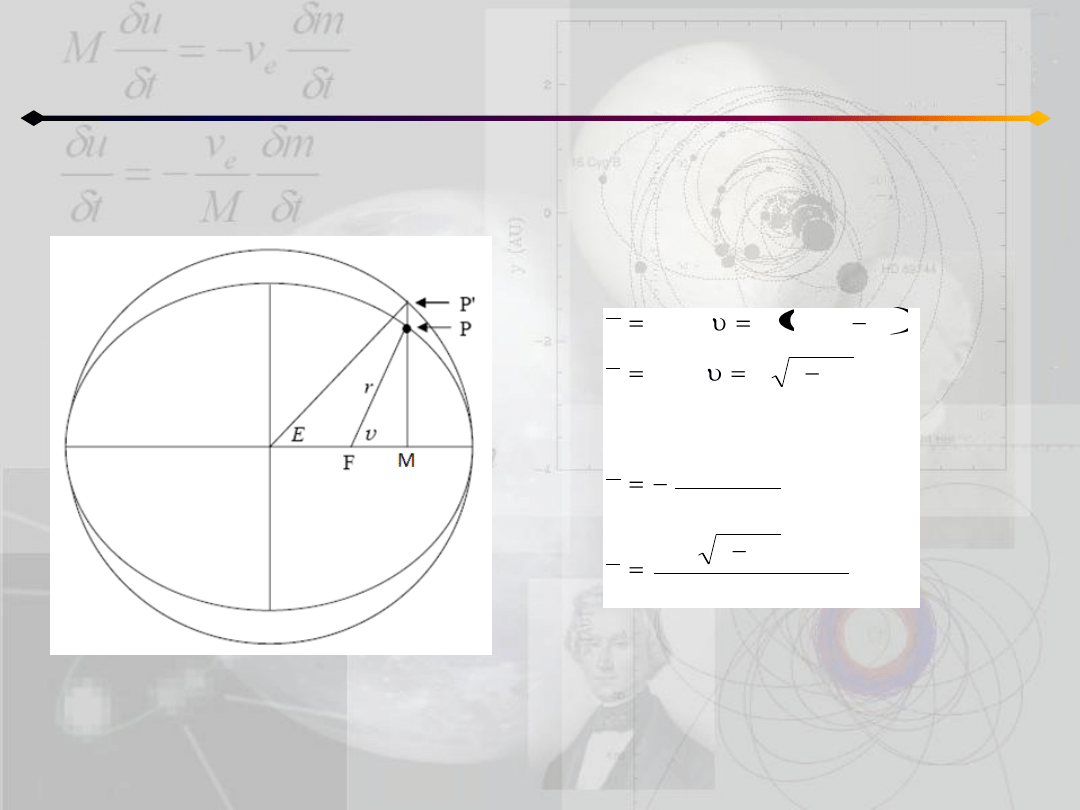
Położenie punktu na orbicie

h<0

O

Współrzędne prostokątne i składowe 
prędkości wyznaczamy z (dwiczenia):

Wródmy do przypadku h>0 (ruch po hiperboli)

r

E

cos

e

1

n

a

y

r

E

sin

n

a

x

E

sin

e

1

a

sin

r

y

e

E

cos

a

cos

r

x

2

2

2

2





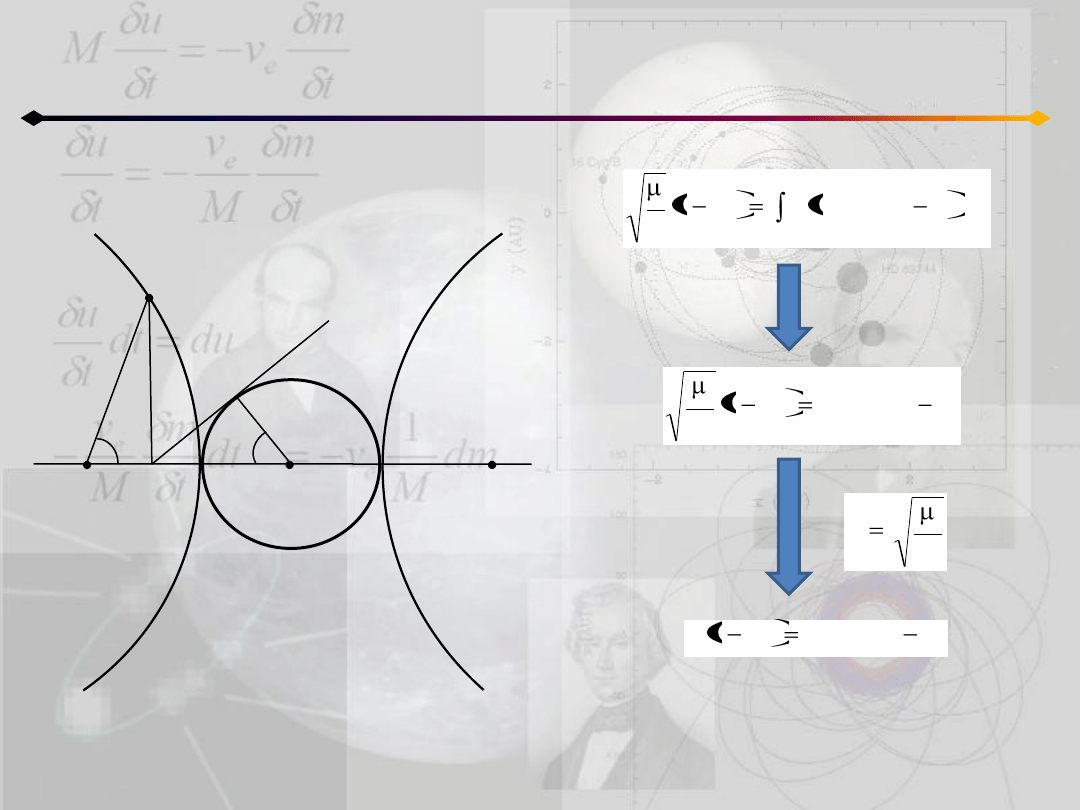
Położenie punktu na orbicie

h<0

S’

S

a

a

P

P’

r

O

Π

Q

υ

H

E

0

dE

1

E

cosh

e

a

T

t

a

E

E

sinh

e

T

t

a

3

całkujemy

oznaczamy:

3

a

n

E

E

sinh

e

T

t

n

E jest hiperboliczną anomalią mimośrodową

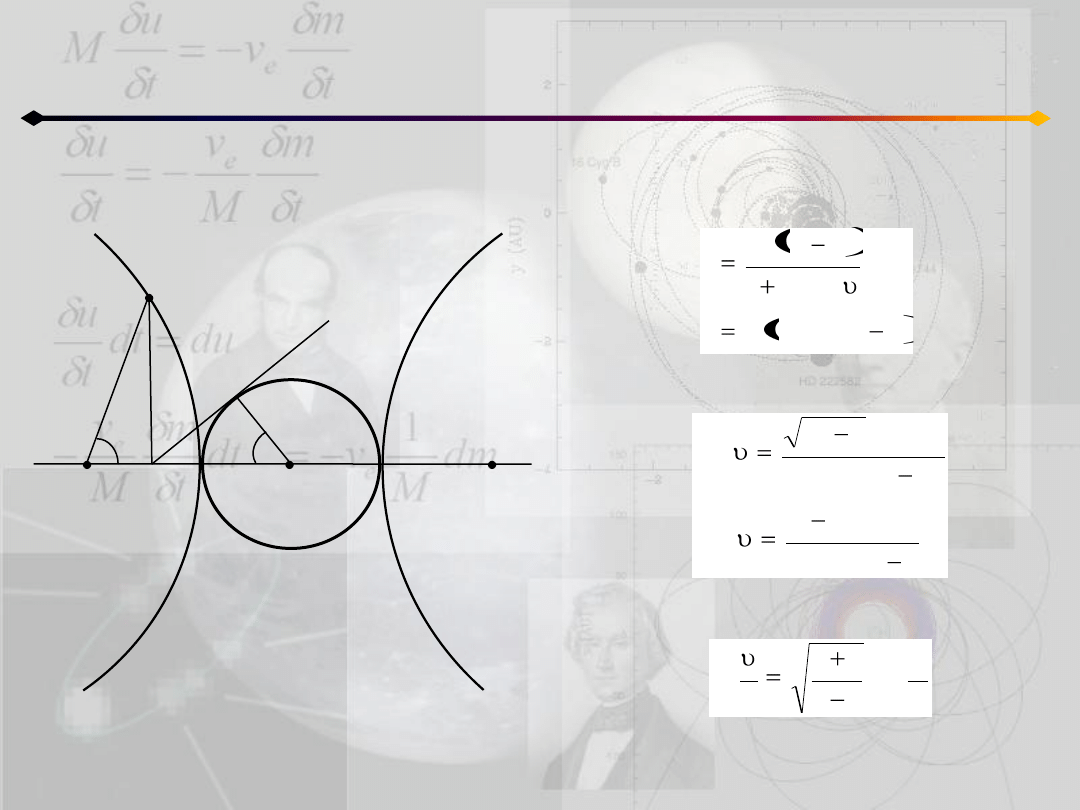
Położenie punktu na orbicie

h<0

S’

S

a

a

P

P’

r

O

Π

Q

υ

H

Porównując równania:

otrzymujemy:

a następnie:

1

E

cosh

e

a

r

cos

e

1

1

e

a

r

2

1

E

cosh

e

E

cosh

e

cos

1

E

cosh

e

E

sinh

1

e

sin

2

2

E

tgh

1

e

1

e

2

tg

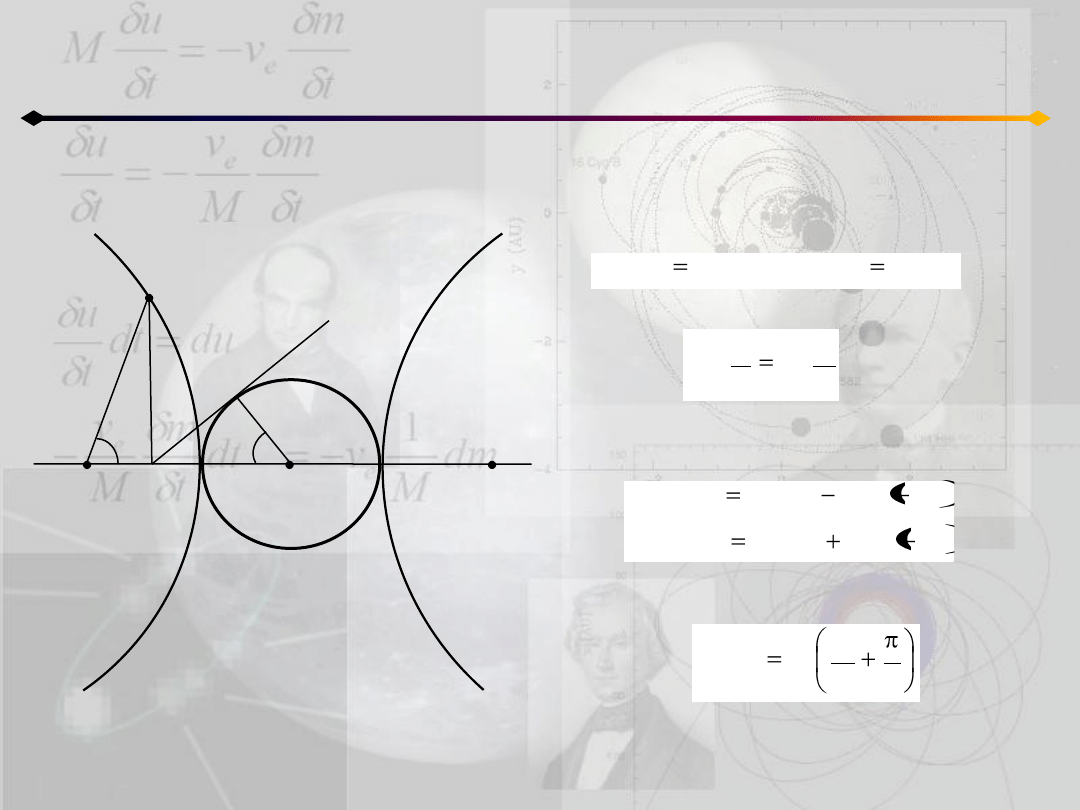
Położenie punktu na orbicie

h<0

S’

S

a

a

P

P’

r

O

Π

Q

υ

H

Uzyskane równania można wyrazid za 
pomocą funkcji trygonometrycznych 
wprowadzając nową zmienną H:

wtedy:

Z definicji funkcji hiperbolicznych:

można pokazad, że:

H

sec

E

cosh

;

H

tg

E

sinh

2

H

tg

2

E

tgh

4

2

H

tg

E

exp

E

exp

E

exp

E

cosh

2

E

exp

E

exp

E

sinh

2