MECHANIKA NIEBA

WYKŁAD 11

21.05.2008 r

Zagadnienie n ciał

Prolog – jeszcze o symulacjach

Przykłady rozwiązao numerycznych 3 i więcej ciał:

Moving Stars Around

Zagadnienie 3 ciał w przypadku dwóch stałych centrów grawitacji

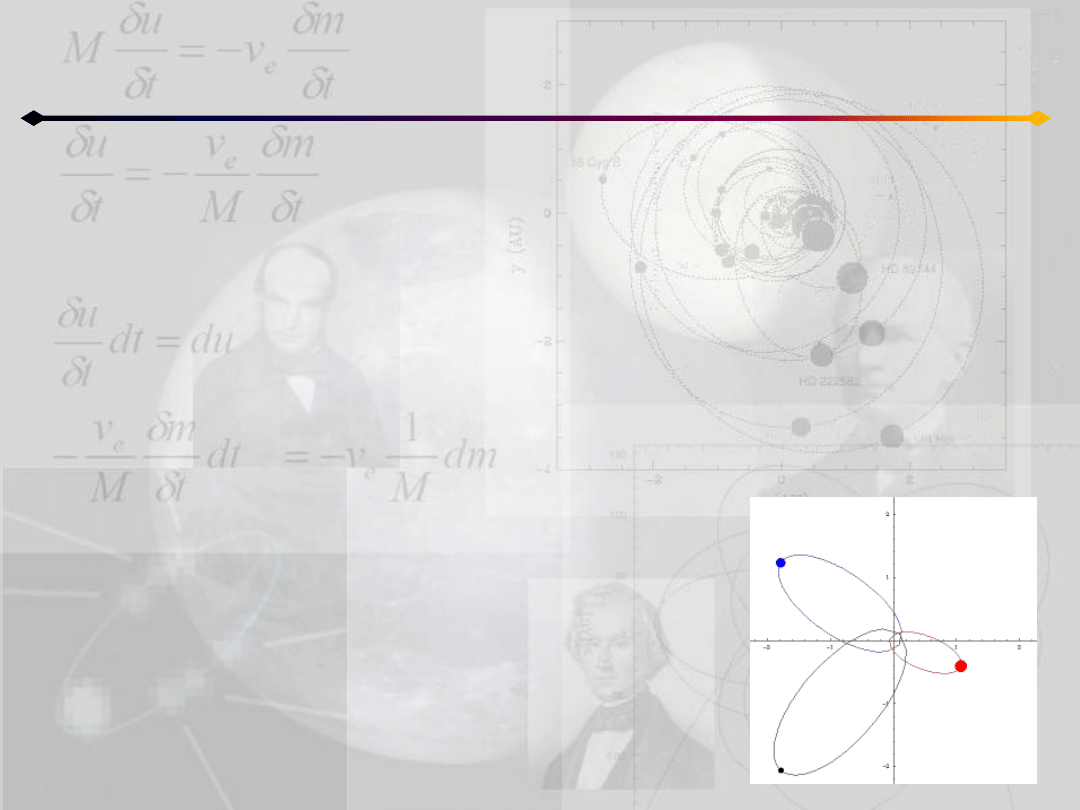
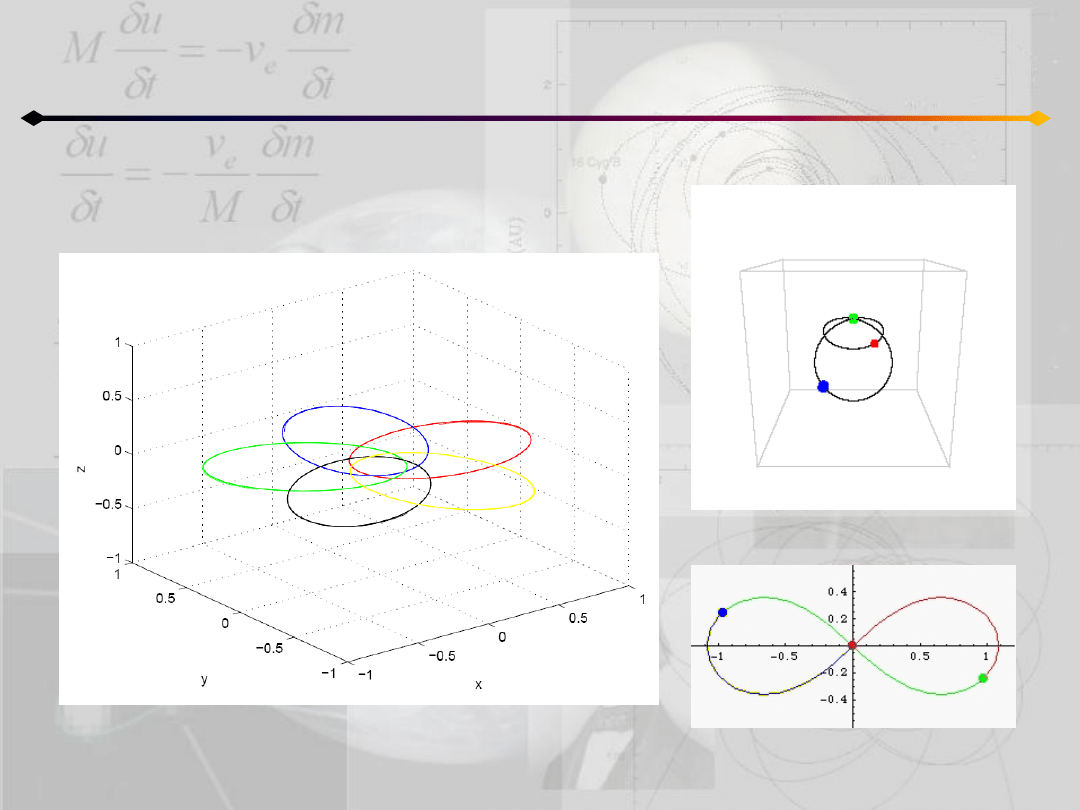
Przykłady rozwiązao szczególnych dla 3 i 4 ciał

Numeryczne rozwiązania zagadnienia n ciał

Zagadnienie n ciał

Zagadnienie n ciał

Rozwiązania szczególne

Duża częśd rozwiązao szczególnych jest uogólnieniem znanych rozwiązao dla układu 3 ciał.

Znane rozwiązania dla n ciał można podzielid na kilka klas:

1. płaskie – jeśli w zagadnieniu n ciał możemy w każdym momencie zdefiniowad

płaszczyznę zawierającą wszystkie ciała. Dodatkowo, jeśli płaszczyzna nie zmienia
swojego położenia w czasie to mówimy o rozwiązaniach jednopłaszczyznowych

2. współliniowe – w przypadku gdy dla dowolnego momentu czasu wszystkie ciała

znajdują się na jednej prostej

3. homograficzne – kształt utworzony przez n ciał względem

barycentrum jest zachowany, przykład:

Zagadnienie n ciał

Rozwiązania szczególne

Zagadnienie n ciał

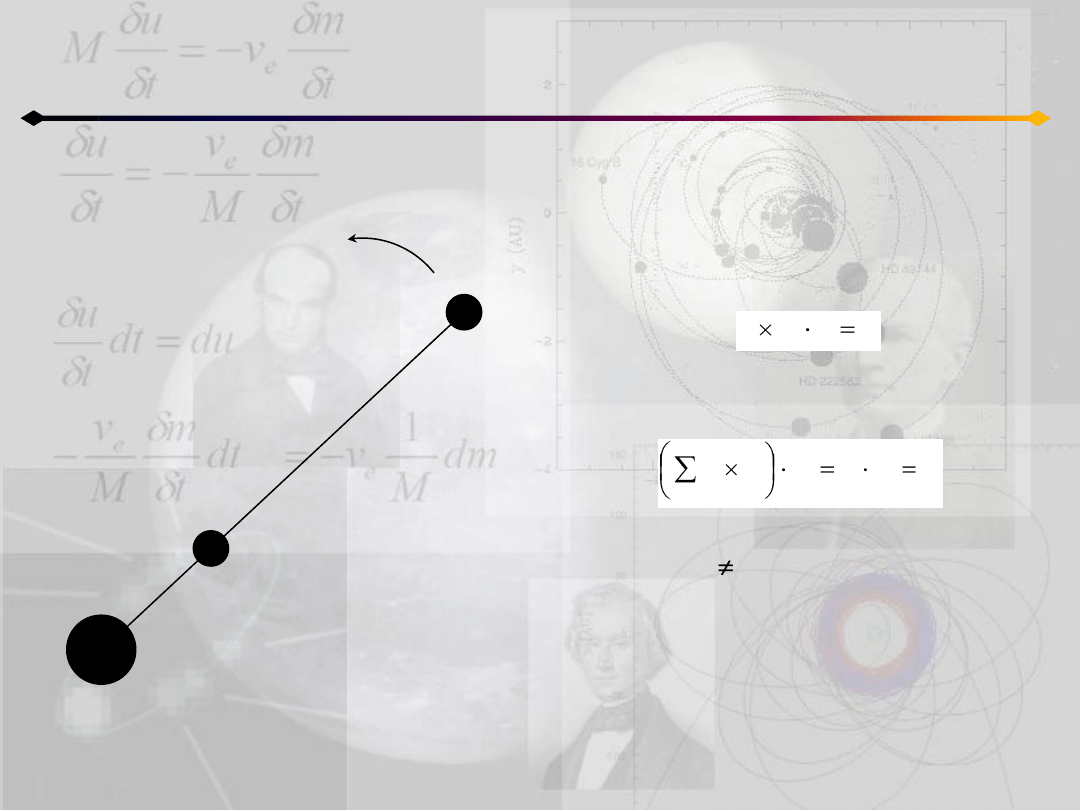
Rozwiązania szczególne - współliniowe

Układ jest współliniowy jeśli w danej
chwili t=t

0

wszystkie ciała leżą na jednej

prostej

Można pokazad, że jeżeli istnieje płaszczyzna
niezmiennicza dla tego układu to ta linia
leży w tej właśnie płaszczyźnie

Dla momentu t=t

0

, każda dowolna para

dwóch punktów leży na jednej linii z
początkiem układu współrzędnych, czyli:

n

,

,

2

,

1

k

,

i

,

0

r

r

k

i







Zagadnienie n ciał

Rozwiązania szczególne - współliniowe

Mnożąc skalarnie przez wektor prędkości
otrzymujemy:

sumując po i:

czyli równanie płaszczyzny niezmienniczej
(ponieważ c 0)

0

r

r

r

i

k

i







0

r

c

r

r

r

k

k

i

i

i











Zagadnienie n ciał

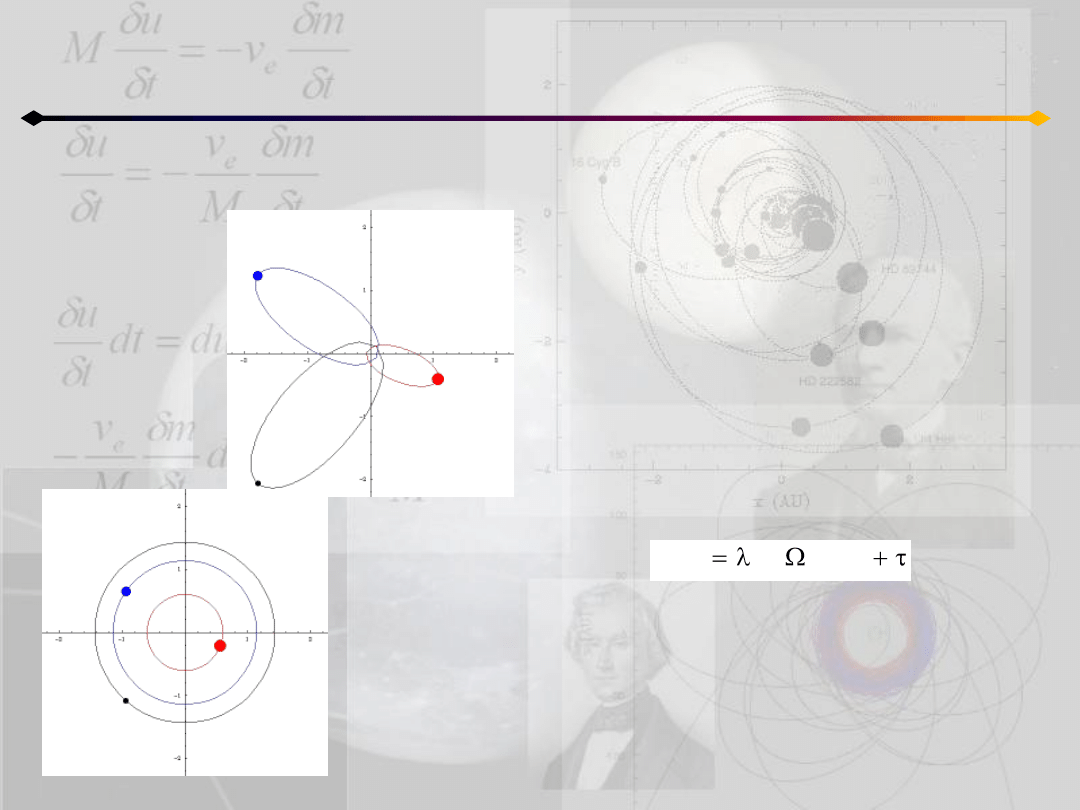
Rozwiązania szczególne - homograficzne

Rozwiązanie homograficzne układu równao
opisującego zagadnienie n ciał odpowiada
przypadkowi, w którym jest zachowana
konfiguracja ciał.

Układ (względem barycentrum) jest
podobny do samego siebie.

To oznacza, że istnieje taka skalarna funkcja
λ=λ(t) oraz ortogonalna macierz (3x3) Ω=Ω(t),
że:

gdzie λ(t) reprezentuje skrócenie (wydłużenie),
a Ω opisuje obrót. Wektor τ opisujący translację
układu jest równy 0, ze względu na
barycentryczny układ współrzędnych.

r

k

o

opisuje układ ciał w momencie t

0

.









o

k

k

r

)

t

(

)

t

(

)

t

(

r

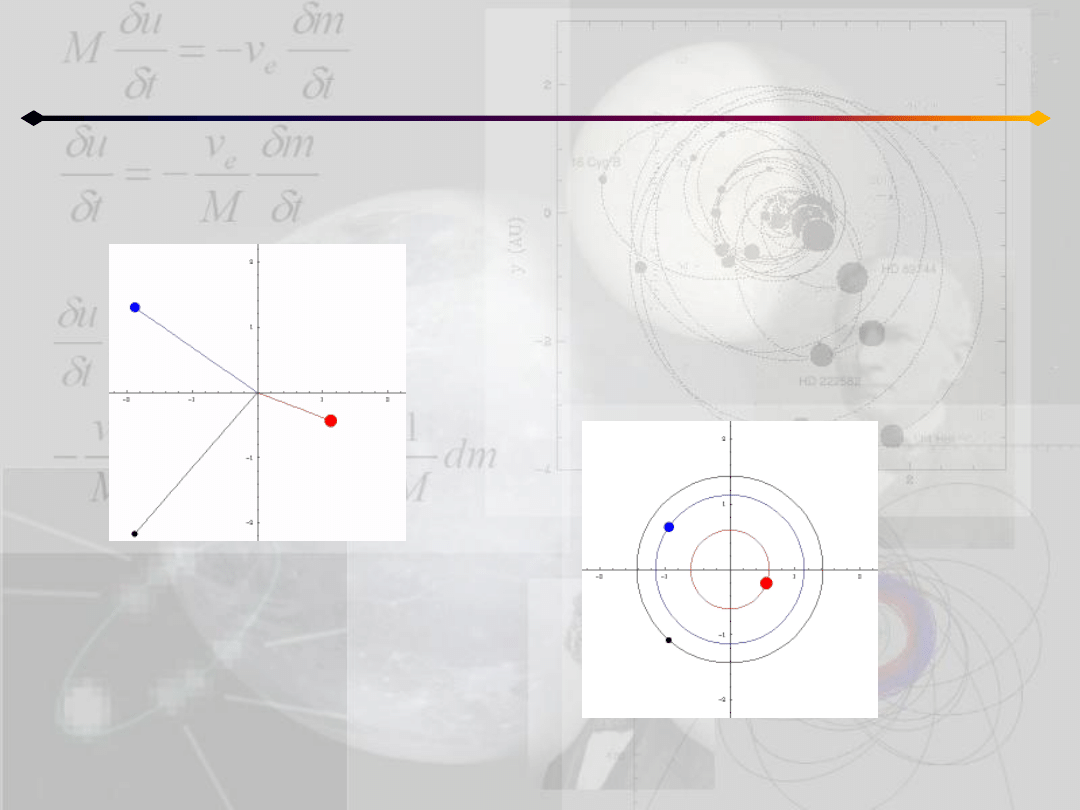
Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

W przypadku homograficznym stosunki
wektorów wodzących ciał są stałe

Ω=1

λ=1

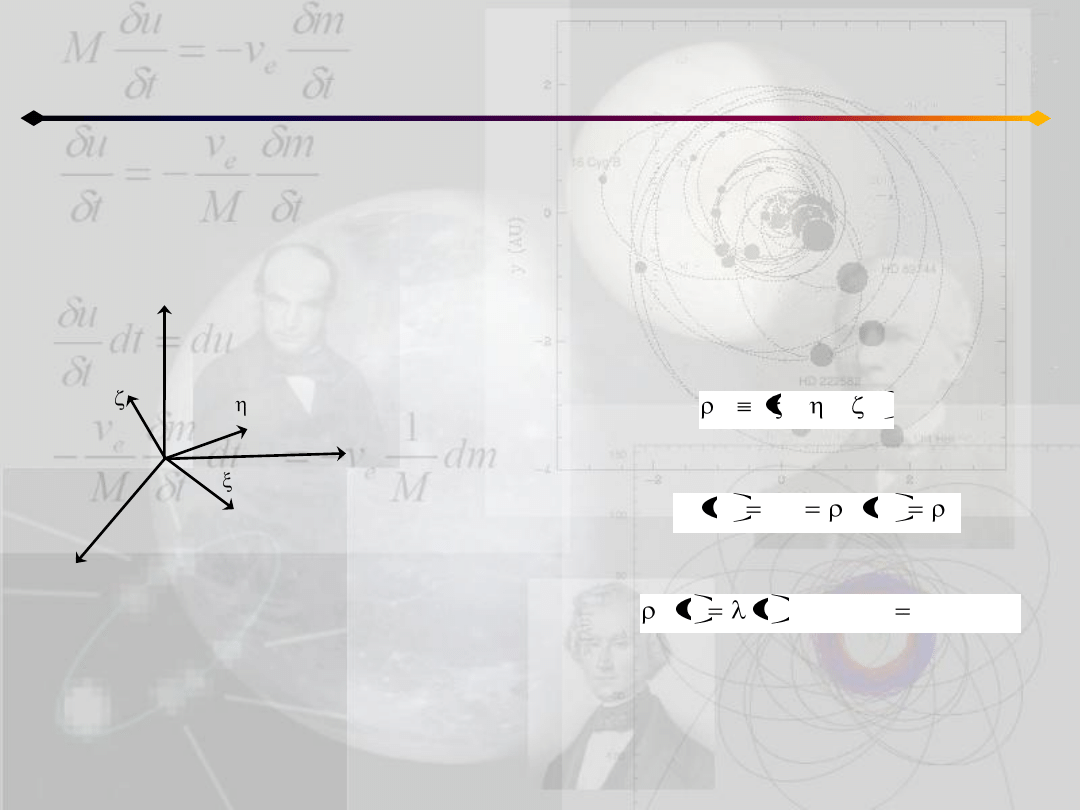
Wyprowadzimy teraz równania ruchu homograficznego.
W tym celu wprowadzamy do układu (x,y,z) drugi
układ (ξ,η,ζ), którego osie mogą zmieniad długośd i rotowad
wokół początku układu. Wektor wodzący ciała k:

wtedy w momencie czasu t=t

0

:

a w dowolnej innej chwili:

Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

o

k

0

k

o

k

0

k

t

r

t

r









n

,

,

2

,

1

k

,

r

t

t

o

k

k







k

k

k

k

,

,



z

y

x

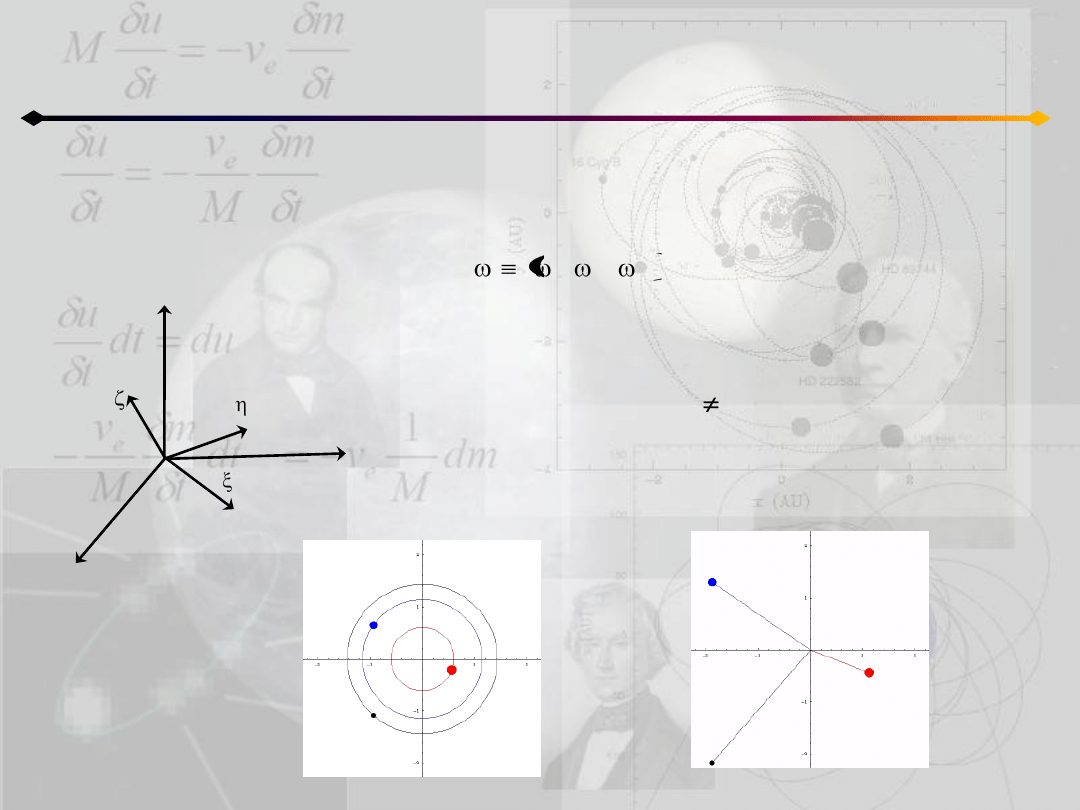
Niech

będzie prędkością kątową

układu (ξ,η,ζ) względem układu barycentrycznego
(x,y,z), wtedy:

a) dla λ=const>0 i ω=const 0 ruch jest we względnej

równowadze

b) dla λ=λ(t)>0 oraz ω=0 mamy do czynienia z ruchem

jednokładnym

Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

z

y

x

3

2

1

,

,



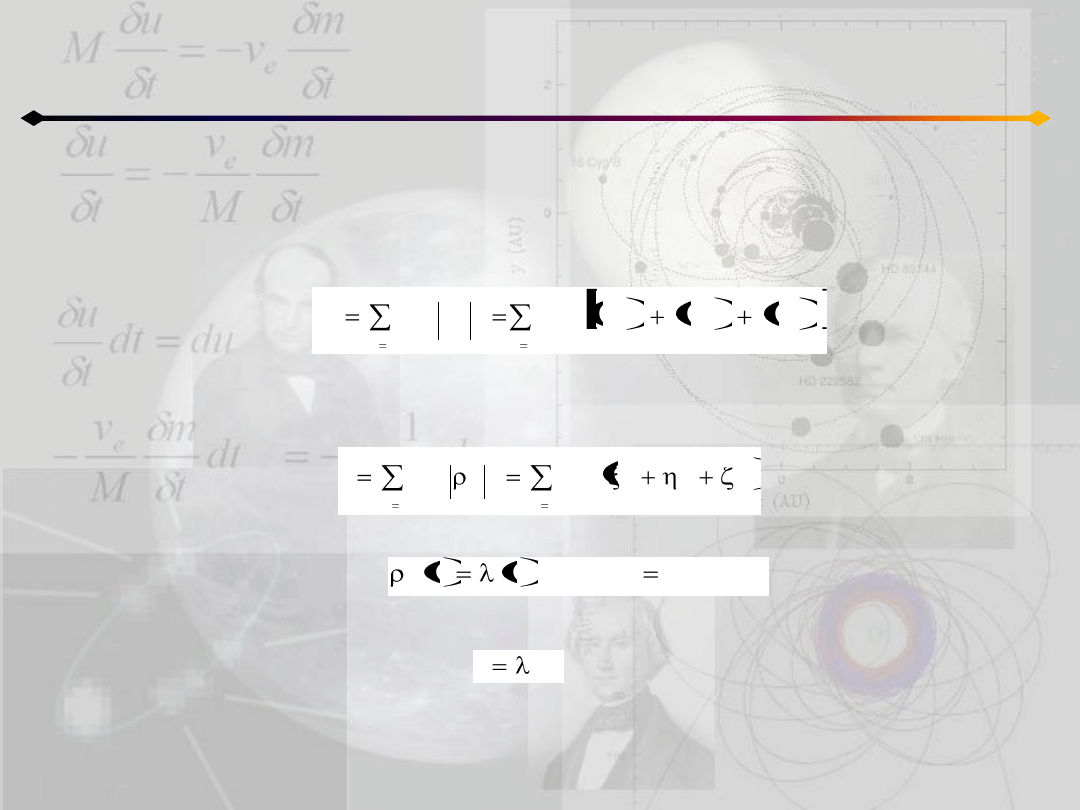
Moment bezwładności w chwili t

0

:

Natomiast w układzie (ξ,η,ζ) w dowolnym innym momencie czasu:

stąd i z równania:

można zauważyd, że:

Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

n

1

k

2

o

k

2

o

k

2

o

k

k

n

1

k

2

o

k

k

o

z

y

x

m

r

m

I



n

1

k

n

1

k

2

k

2

k

2

k

k

2

k

k

m

m

I



o

2

I

I

n

,

,

2

,

1

k

,

r

t

t

o

k

k







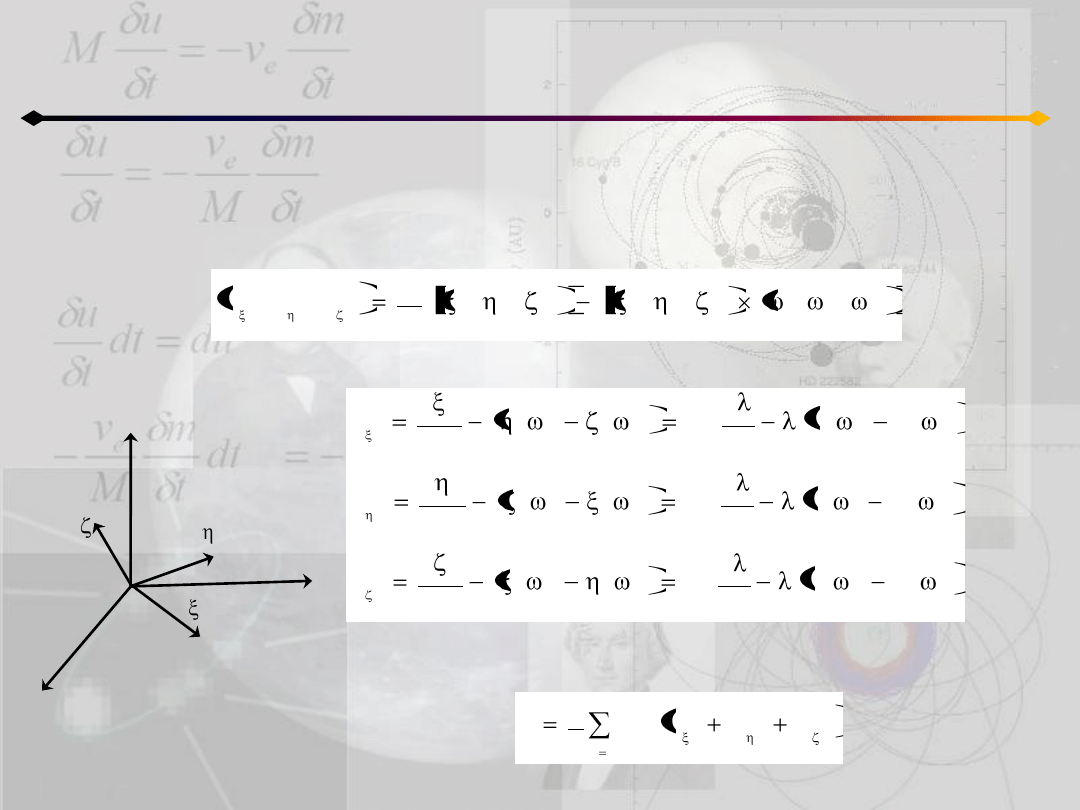
Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

Składowe prędkości k-tego ciała w układzie (ξ,η,ζ) są równe:

skąd:

Natomiast energia kinetyczna:

3

2

1

k

k

k

k

k

k

k

k

k

,

,

,

,

,

,

dt

d

v

,

v

,

v

1

o

k

2

o

k

o

k

1

k

2

k

k

k

3

o

k

1

o

k

o

k

3

k

1

k

k

k

2

o

k

3

o

k

o

k

2

k

3

k

k

k

y

x

dt

d

z

dt

d

v

x

z

dt

d

y

dt

d

v

z

y

dt

d

x

dt

d

v

n

1

k

2

k

2

k

2

k

k

v

v

v

m

2

1

T

z

y

x

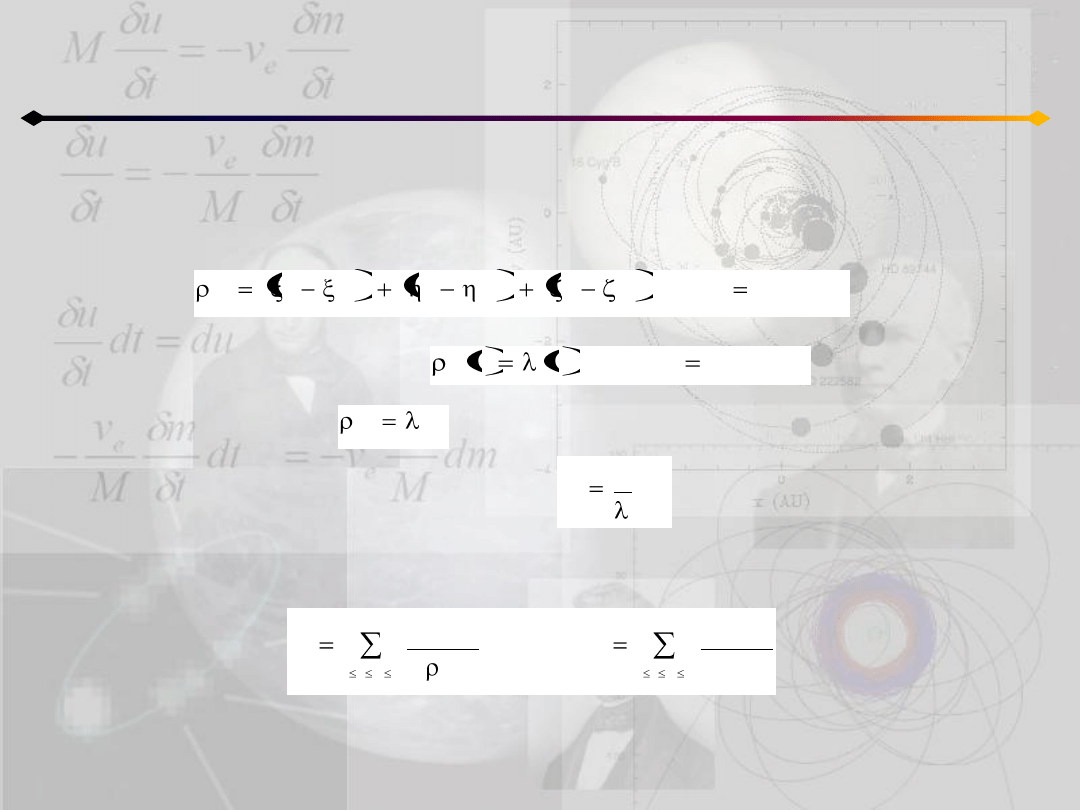
Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

Odległośd między dwoma masami m

j

i m

k

:

znów korzystamy z równania

możemy napisad:

ostatecznie dostajemy dla potencjałów:

gdzie (dla układu jednostek, w którym G=1):

n

,...,

2

,

1

k

,

j

,

2

k

j

2

k

j

2

k

j

2

jk

n

,

,

2

,

1

k

,

r

t

t

o

k

k







o

jk

jk

r

o

U

1

U

n

k

j

1

o

jk

k

j

o

n

k

j

1

jk

k

j

r

m

m

U

m

m

U

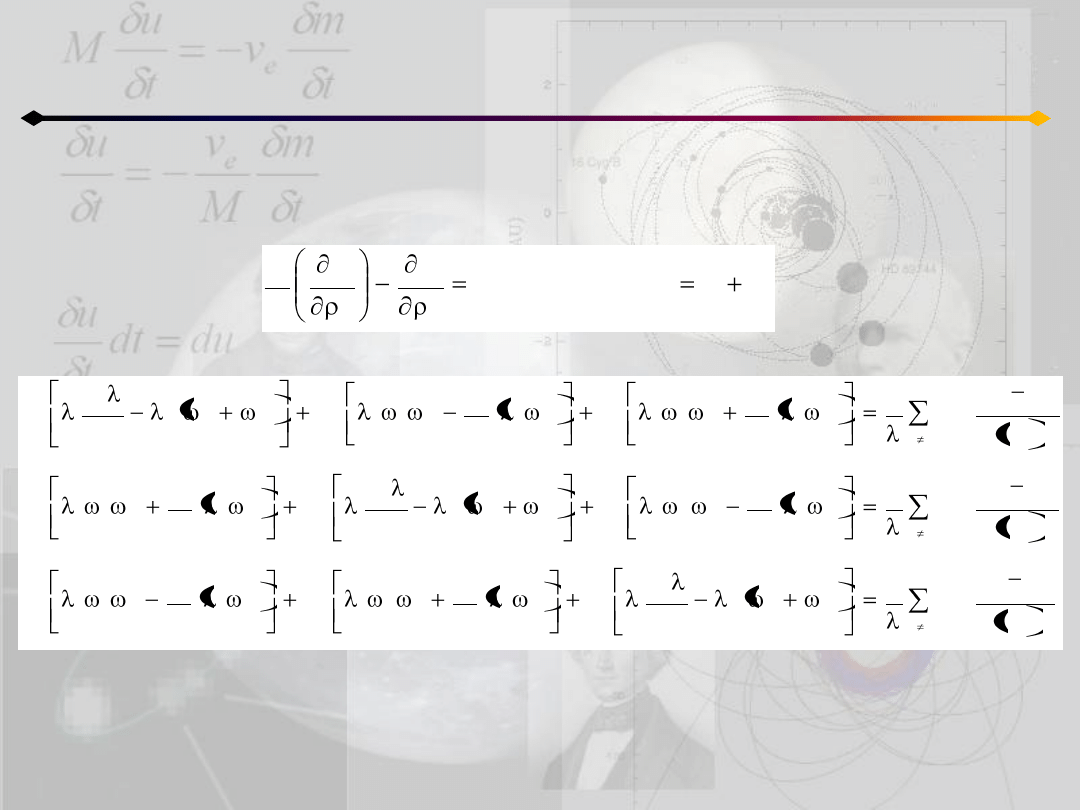
Zagadnienie n ciał

Rozwiązania szczególne - homograficzne

Podstawiając otrzymane wyrażenia do równania Lagrange’a II-go rodzaju:

otrzymujemy ostatecznie (11.1):

równania ruchu homograficznego dla j-tego ciała. Istnieją trzy szczególne
przypadki tego ruchu: a) współliniowy, b) płaski i c) przestrzenny (dla n>=4).

U

T

L

:

gdzie

0

L

L

dt

d

k

k





j

k

3

o

jk

o

j

o

k

k

2

2

2

1

2

2

2

o

j

1

2

3

2

2

o

j

2

2

3

1

2

o

j

j

k

3

o

jk

o

j

o

k

k

1

2

3

2

2

o

j

2

1

2

3

2

2

2

o

j

3

2

2

1

2

o

j

j

k

3

o

jk

o

j

o

k

k

2

2

3

1

2

o

j

3

2

2

1

2

o

j

2

3

2

2

2

2

2

o

j

r

z

z

m

1

dt

d

z

dt

d

y

dt

d

x

r

y

y

m

1

dt

d

z

dt

d

y

dt

d

x

r

x

x

m

1

dt

d

z

dt

d

y

dt

d

x

Zagadnienie n ciał

Ruch homograficzny współliniowy

Z takim rodzajem ruchu mamy do czynienia kiedy
wszystkie n ciał znajdują się na jednej linii.

Jeśli przyjmiemy, że tą linią jest oś ξ to dla
każdego k w momencie t

0

mamy:

oprócz tego dla dowolnego k w każdym innym
momencie czasu:

0

z

y

o

k

o

k

0

k

k

z

y

x

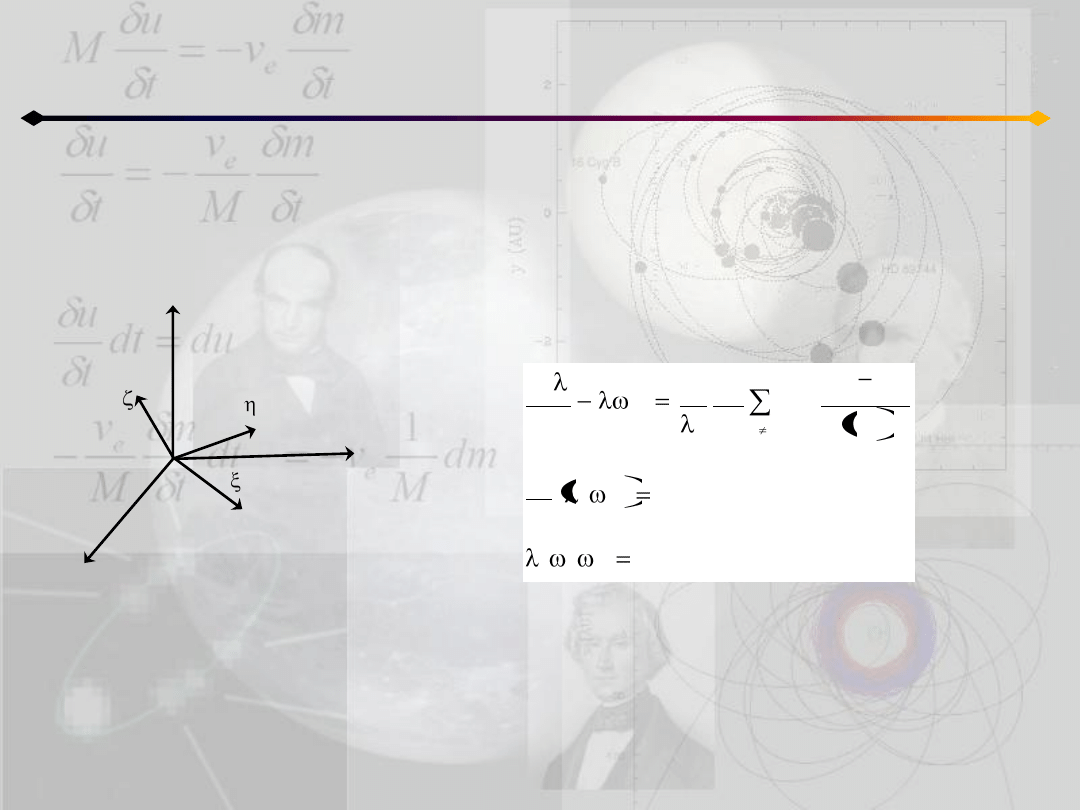
Zagadnienie n ciał

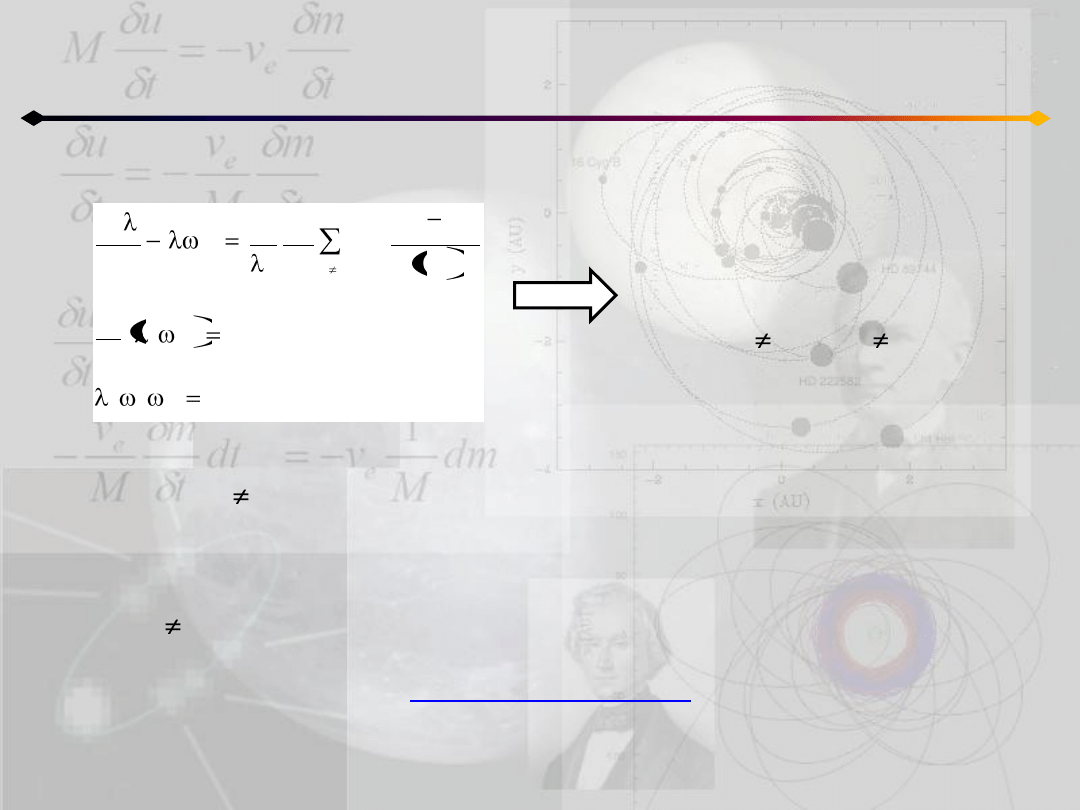
Ruch homograficzny współliniowy

Poza tym można tak dobrad oś η w taki sposób,
że ω

2

=0 i wtedy układ 11.1 przyjmuje postad:

0

0

dt

d

r

x

x

m

x

1

1

dt

d

3

1

2

3

2

j

k

3

o

jk

o

j

o

k

k

o

j

2

2

3

2

2

(11.2)

z

y

x

Zagadnienie n ciał

Ruch homograficzny współliniowy

0

0

dt

d

r

x

x

m

x

1

1

dt

d

3

1

2

3

2

j

k

3

o

jk

o

j

o

k

k

o

j

2

2

3

2

2

Z ostatnich dwóch równao
wynika, że:

ω

3

=0 i ω

1

0, lub ω

3

0 i ω

1

=0

1. ω

3

=0 i ω

1

0. Ponieważ jednocześnie ω

2

=0, więc oś ξ jest nieruchoma i ruch

odbywa się po linii prostej mającej ustalone położenie w przestrzeni. Poza tym
całkowity moment pędu znika (η

k

=ζ

k

=0 oraz v

ηk

=v

ζk

=0) i ruch jest jednokładny

2. ω

3

0 i ω

1

=0. W tym wypadku λ

2

ω

3

=const=α, a oś ξ nie jest nieruchoma tylko

rotuje wokół osi ζ, która tym razem jest nieruchoma. Ruch odbywa się w
płaszczyźnie ζ=0 i będzie to

ruch jednopłaszczyznowy

, z płaszczyzną ξη nieruchomą

w przestrzeni

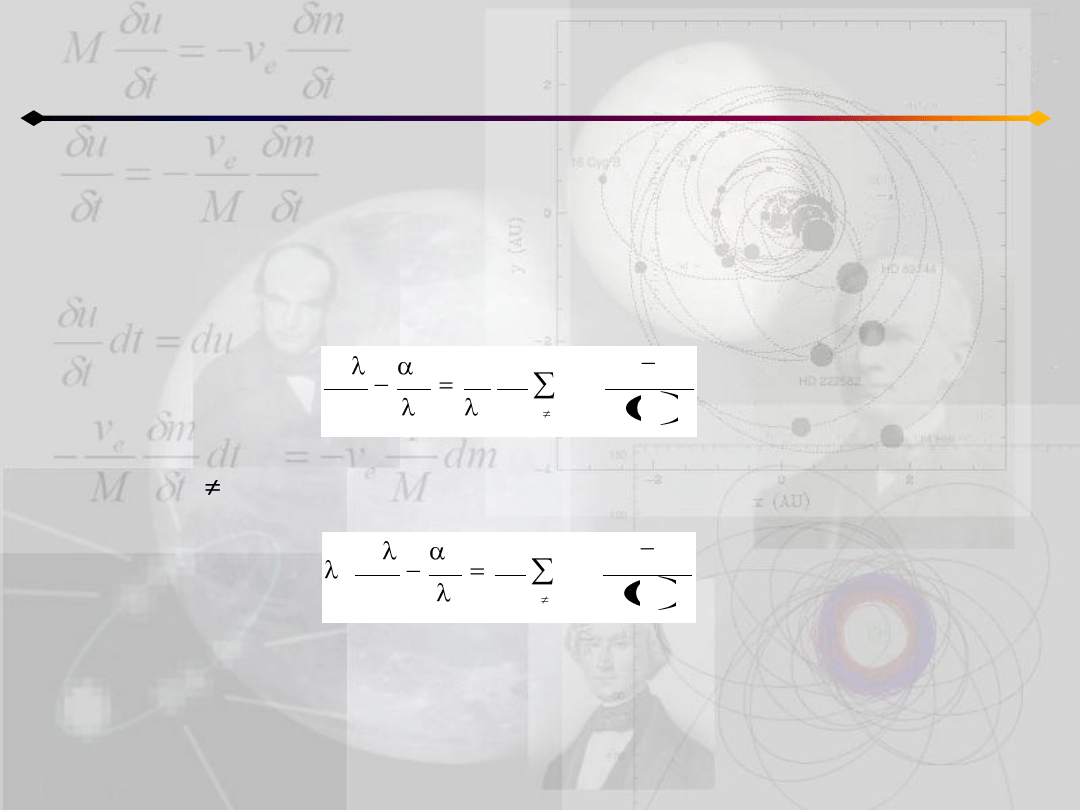
Zagadnienie n ciał

Ruch homograficzny współliniowy

Oba powyższe przypadki można sprowadzid do jednego (bo pierwsze z równao 11.2
nie zawiera ω

1

) podstawiając za ω

3

wyrażenie α/λ

2

(wtedy pierwszy przypadek

odpowiada α=0):

ponieważ λ 0, więc możemy powyższe przepisad w postaci:

skąd można zauważyd, że prawa strona jest stała (a więc lewa również).

j

k

3

o

jk

o

j

o

k

k

o

j

2

3

2

2

2

r

x

x

m

x

1

1

dt

d

j

k

3

o

jk

o

j

o

k

k

o

j

2

2

2

2

r

x

x

m

x

1

dt

d

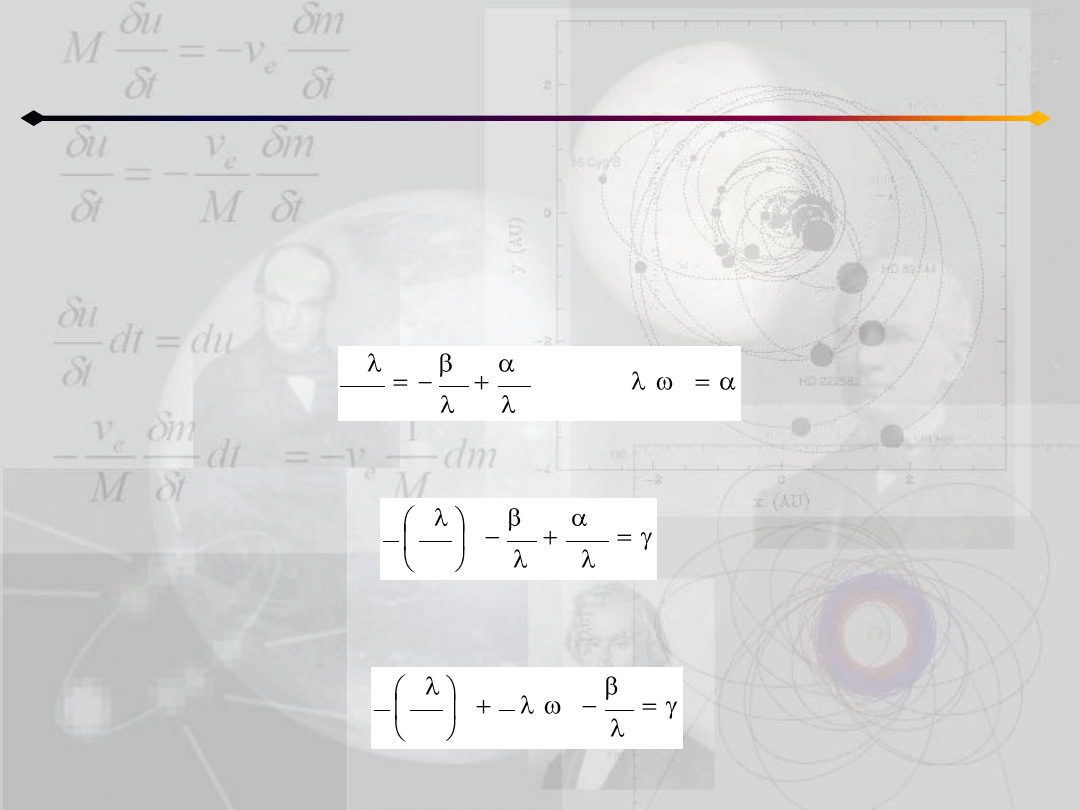
Zagadnienie n ciał

Ruch homograficzny współliniowy

Wprowadzając w miejsce prawej strony wyrażenie –β

2

(minus oznacza, że siła jest

przyciągająca) możemy przekształcid otrzymane równania do postaci:

mnożąc obustronnie pierwsze równanie przez dλ/dt i całkując dostajemy:

gdzie γ jest stałą całkowania. Podstawiając drugie równanie mamy ostatecznie:

3

2

3

2

2

2

2

2

;

dt

d

2

2

2

2

2

dt

d

2

1

2

2

3

2

2

2

1

dt

d

2

1

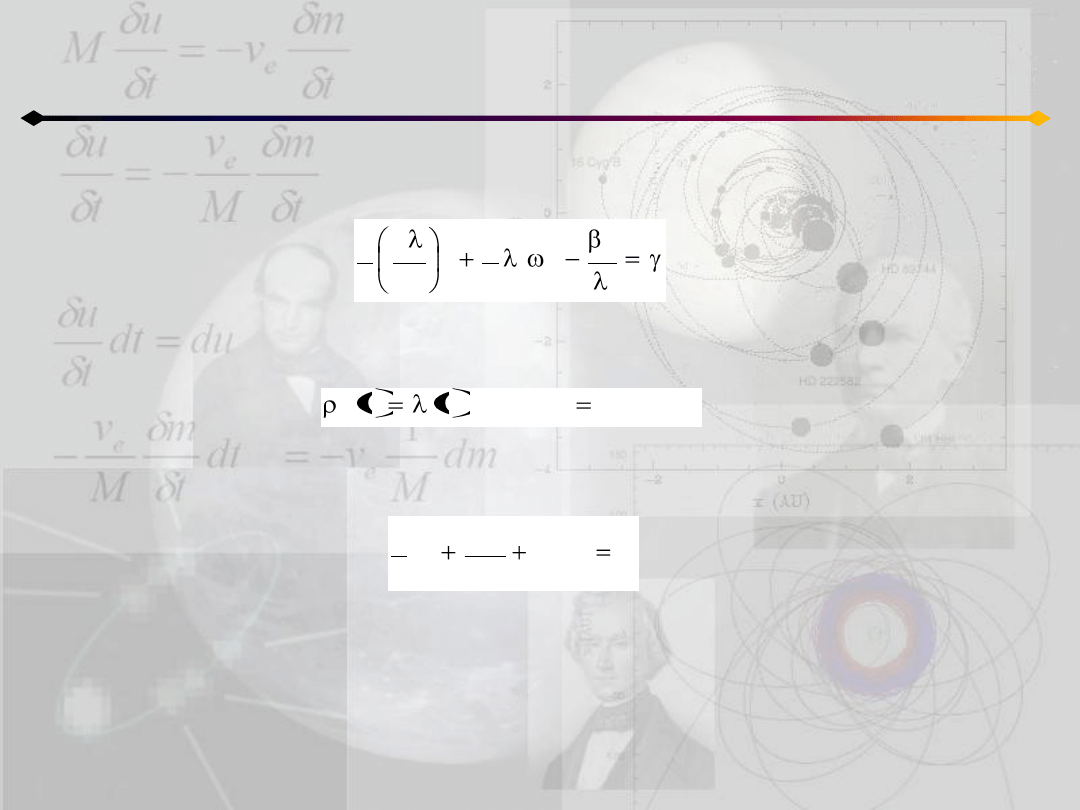
Zagadnienie n ciał

Ruch homograficzny współliniowy

Pamiętając, że:

możemy zauważyd, że otrzymane równanie jest tożsame z równaniem energii
ruchu keplerowskiego:

Jeżeli λ jest stałe to również ω

3

jest stałe i orbity keplerowskie są okręgami – n ciał

znajduje się na jednej linii rotującej ze stałą prędkością ω

3

wokół barycentrum.

Dla α=0 (ω

3

=0), ciała spadają na barycentrum po liniach prostych

2

2

3

2

2

2

1

dt

d

2

1

n

,

,

2

,

1

k

,

r

t

t

o

k

k







h

)

r

(

V

r

2

c

r

2

1

2

2

2



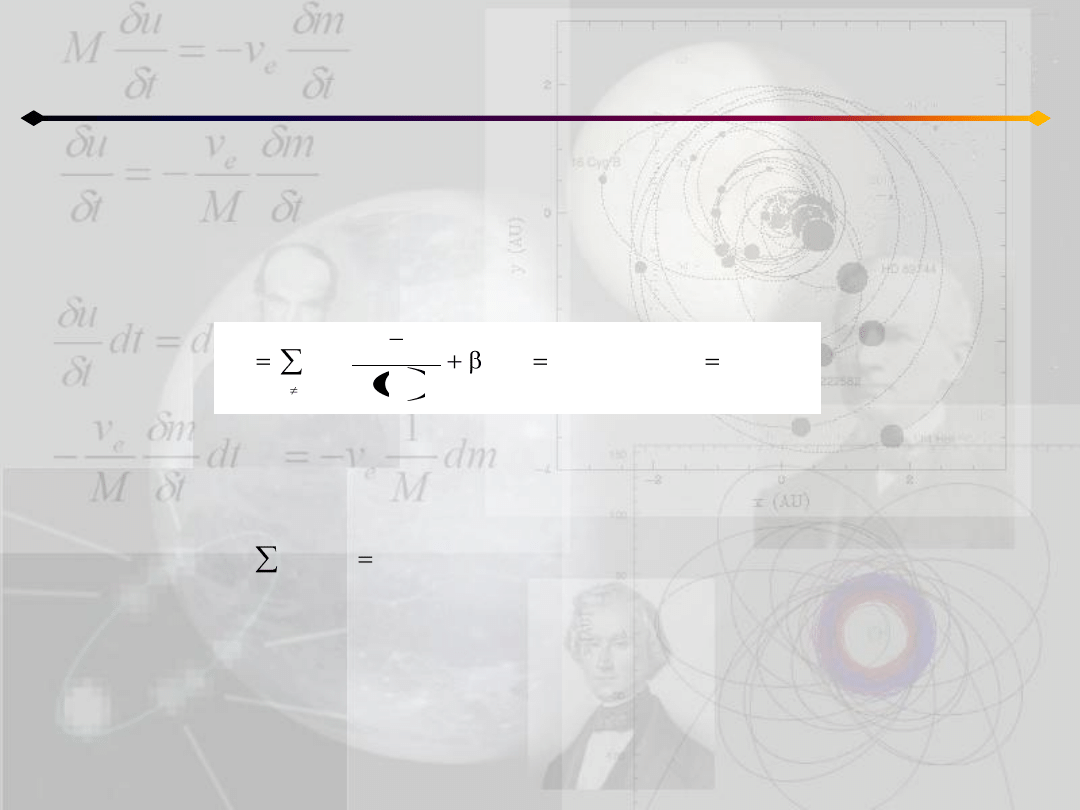
Pamiętając o definicji wprowadzonej wcześniej zmiennej β możemy napisad:

wielkości X

j

zależą tylko od mas i współrzędnych początkowych, więc powyższe

równanie określa n warunków, które muszą byd spełnione aby ruch był homograficzny

Jednak również jest spełnione dla n czynników X

j

, w związku z tym

powyższe równanie określa n-1 warunków dla ruchu homograficznego

Zagadnienie n ciał

Ruch homograficzny współliniowy

n

,...,

2

,

1

k

,

j

0

x

r

x

x

m

X

o

j

2

j

k

3

o

jk

o

j

o

k

k

j

0

X

m

j

j

j

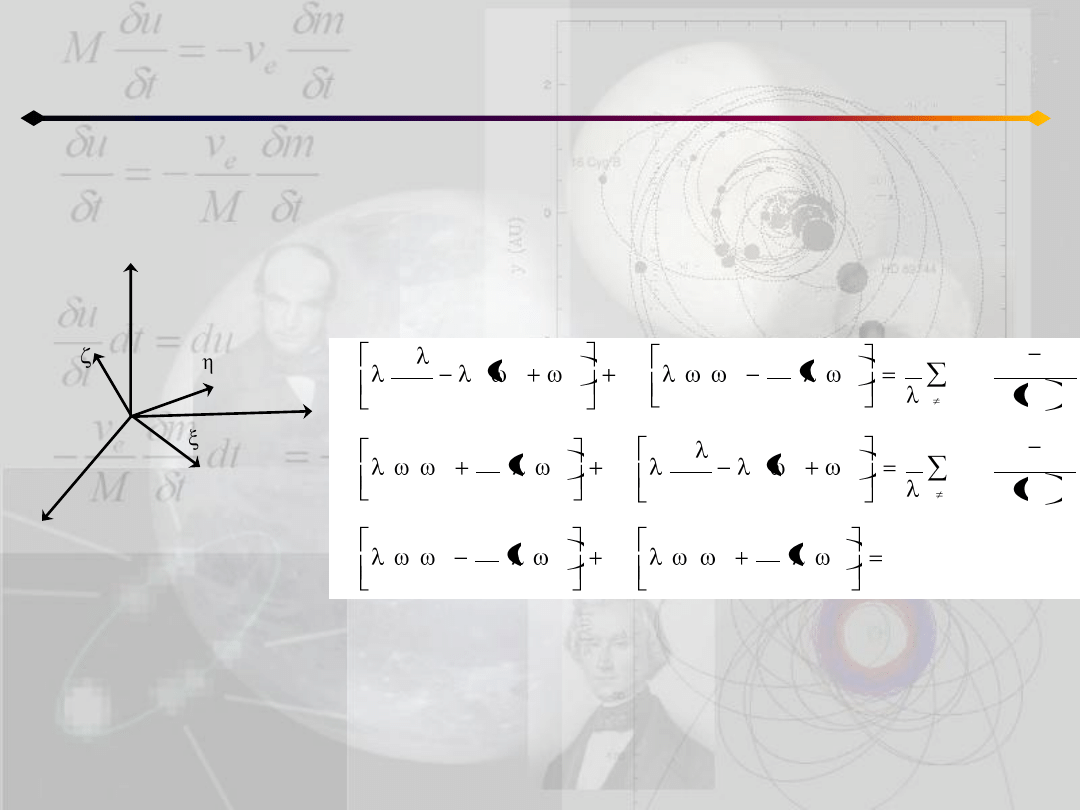
Załóżmy, że początkową płaszczyzną ruchu jest płaszczyzna ζ=0,
wtedy dla każdego k współrzędne z i ζ są równe 0. W takim razie
układ 11.1 przyjmuje postad:

Można pokazad (Boccaletti i Pucacco 2004), że ruch homograficzny
płaski jest jednocześnie jednopłaszczyznowy

Zagadnienie n ciał

Ruch homograficzny płaski

0

dt

d

y

dt

d

x

r

y

y

m

1

dt

d

y

dt

d

x

r

x

x

m

1

dt

d

y

dt

d

x

1

2

3

2

2

o

j

2

2

3

1

2

o

j

j

k

3

o

jk

o

j

o

k

k

2

1

2

3

2

2

2

o

j

3

2

2

1

2

o

j

k

j

3

o

jk

o

j

o

k

k

3

2

2

1

2

o

j

2

3

2

2

2

2

2

o

j

z

y

x

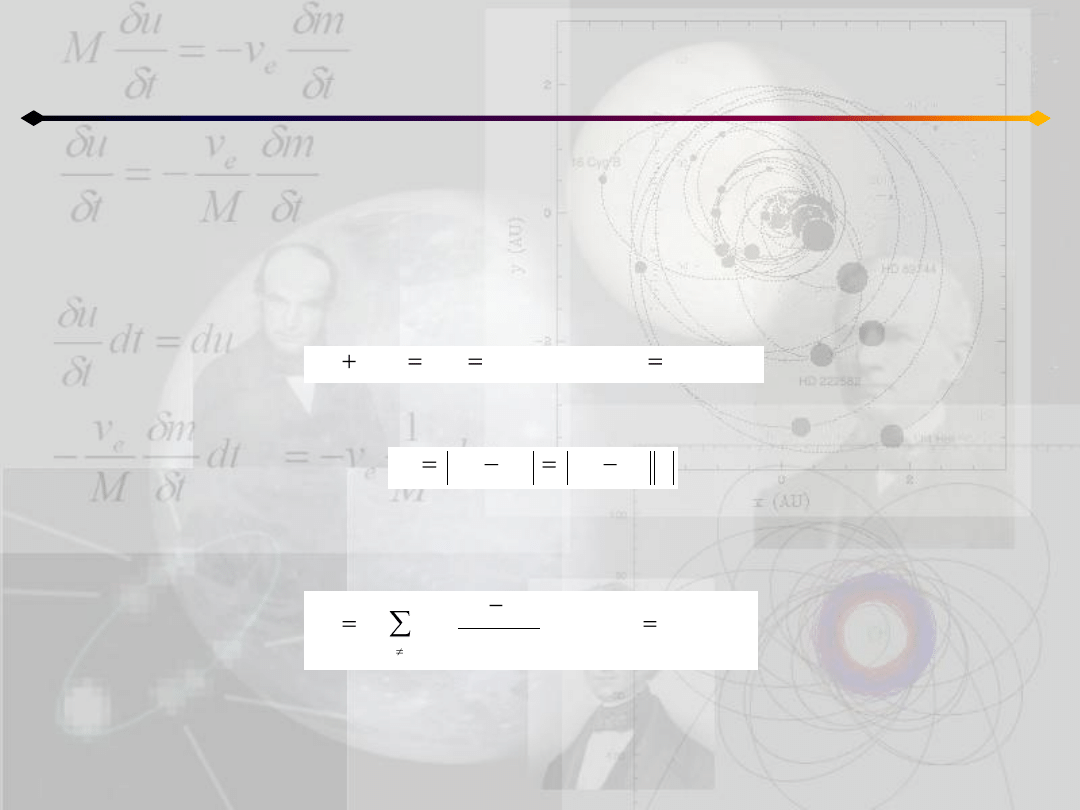
Zagadnienie n ciał

Ruch homograficzny płaski

Jeżeli ruch odbywa się w jednej płaszczyźnie niezmiennej z czasem to wygodnie
jest opisywad ją jako płaszczyznę zespoloną, na której położenia kolejnych mas
są przedstawione liczbami zespolonymi:

gdzie a

k

są zespolonymi stałymi a q jest zespoloną funkcją czasu. Stąd:

Równanie ruchu n-ciał w przypadku ruchu jednopłaszczyznowego zapisane w
postaci zespolonej:

n

,...,

2

,

1

k

)

t

(

q

a

p

iy

x

k

k

k

k

q

a

a

p

p

r

l

k

l

k

kl

n

,...,

2

,

1

l

,

k

r

p

p

m

G

p

k

l

3

kl

k

l

l

k





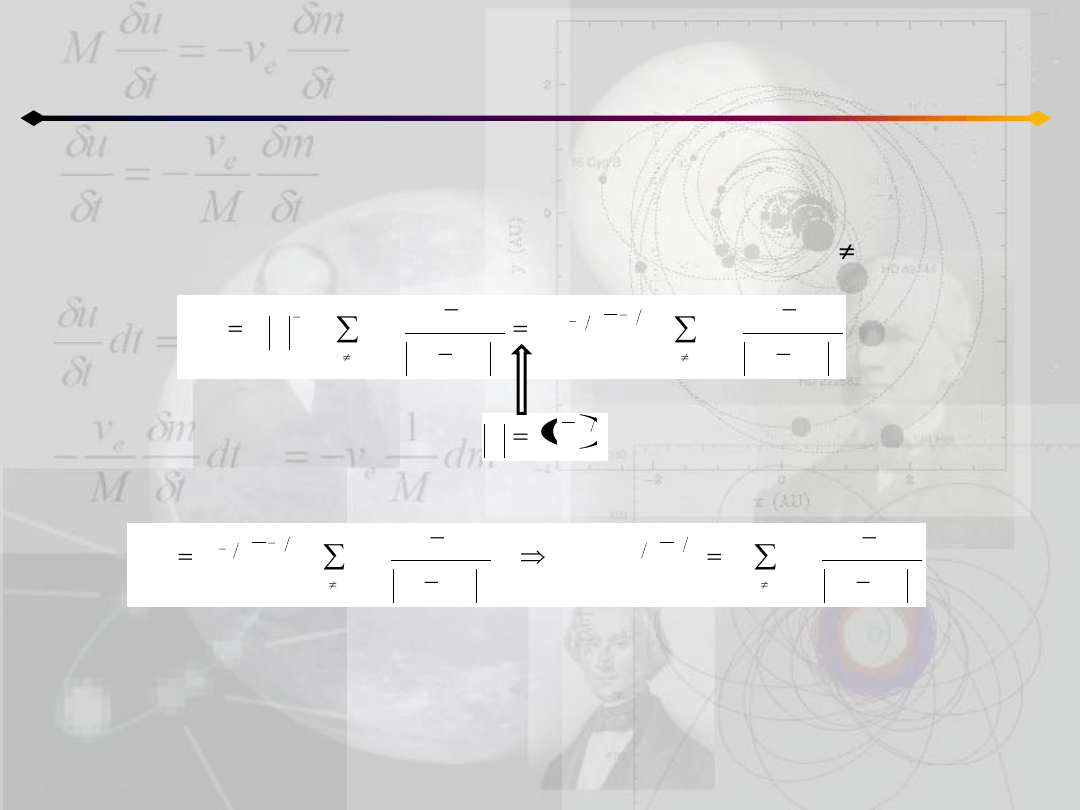
Zagadnienie n ciał

Ruch homograficzny płaski

Podstawiając do równania ruchu wyrażenie na p

k

oraz zakładając q 0 dostajemy:

a następnie:

prawa strona ostatniego równania jest niezależna od czasu.

k

l

3

k

l

k

l

l

2

3

2

3

k

l

3

k

l

k

l

l

3

k

a

a

a

a

m

G

q

qq

a

a

a

a

m

G

q

q

q

a 



2

1

q

q

q

k

l

3

k

l

k

l

l

2

3

2

1

k

k

l

3

k

l

k

l

l

2

3

2

1

k

a

a

a

a

m

G

q

q

q

a

a

a

a

a

m

G

q

q

q

a









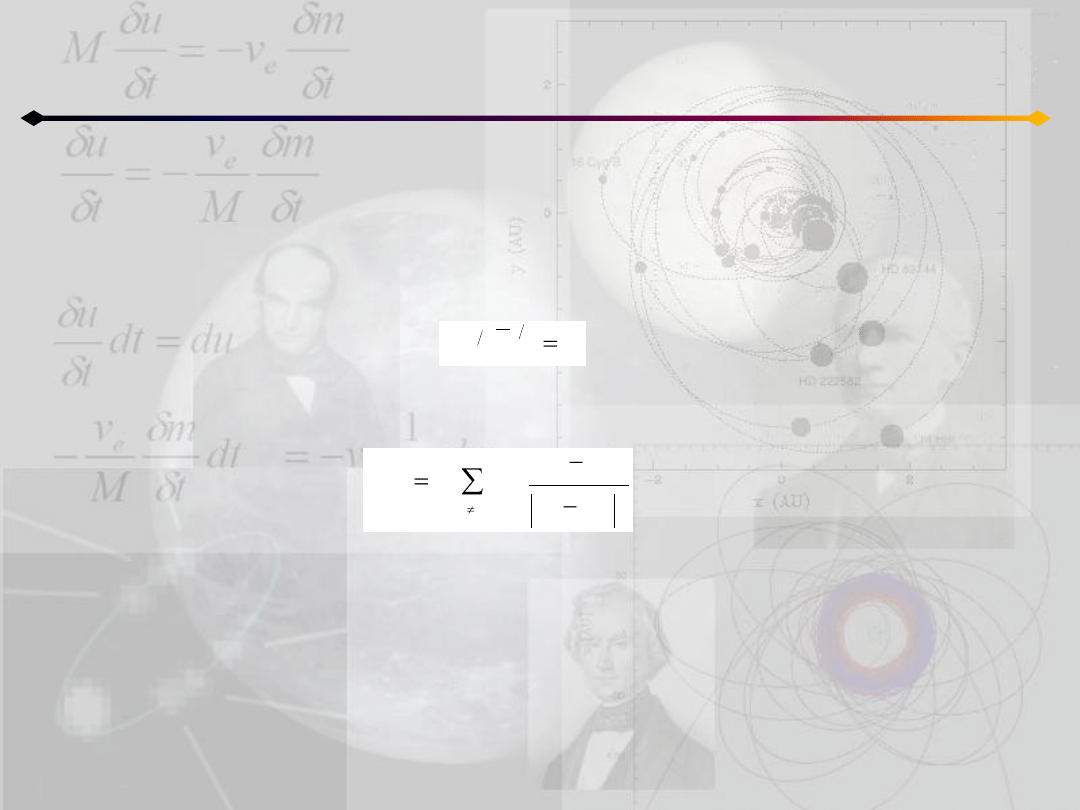
Zagadnienie n ciał

Ruch homograficzny płaski

W takim razie rozpatrywane zagadnienie sprowadza się do znalezienia rozwiązania
równania różniczkowego:

(gdzie b jest stałą niezależną od t, a całe równanie nie zależy od n) uzupełnionego
przez układ równao:

Równanie 11.3a jest niezależne od n więc, możemy znad jego rozwiązanie jeżeli
rozwiążemy je dla przypadku dwóch ciał.

b

q

q

q

2

3

2

1





k

l

3

k

l

k

l

l

k

a

a

a

a

m

G

b

a

(11.3a)

(11.3b)

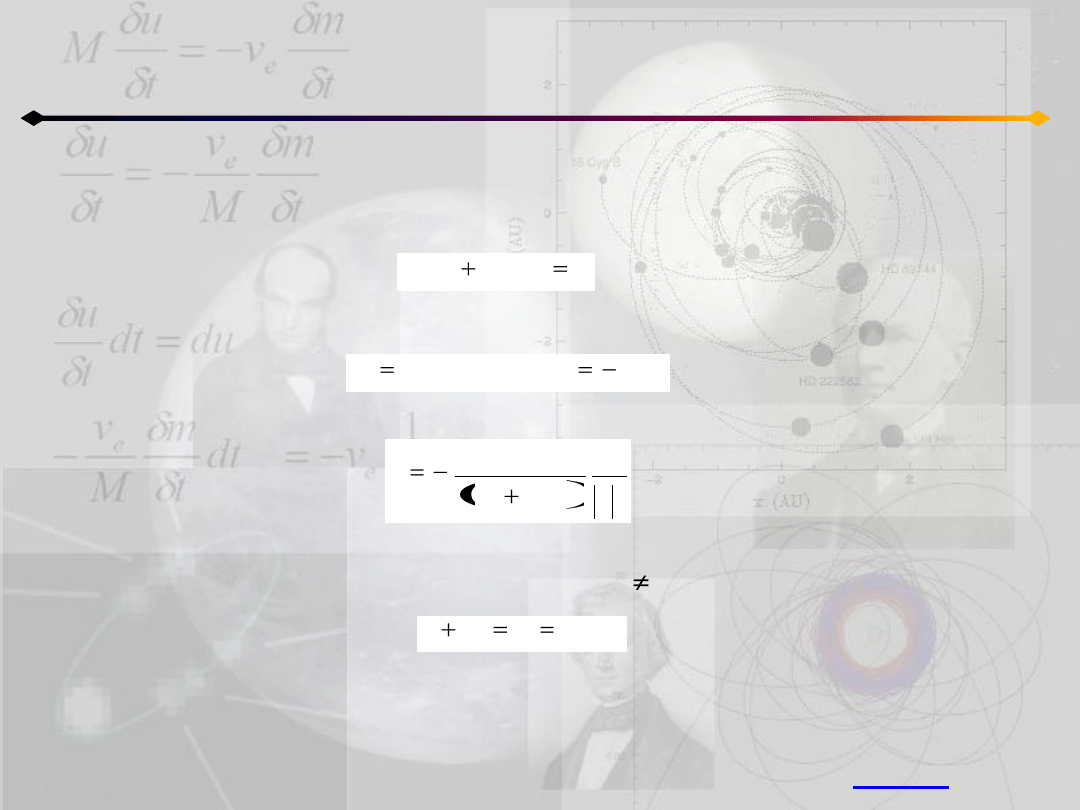
Zagadnienie n ciał

Ruch homograficzny płaski

W przypadku dwóch ciał (we współrzędnych barycentrycznych):

które może byd wyrażone w postaci:

gdzie a jest pewną liczbą zespoloną. Z układu 11.3b otrzymujemy wtedy:

co oznacza, że b jest liczbą rzeczywistą, ujemną. Jeżeli rozwiązaniem układu 11.3a
jest q=q(t) - znana funkcja z parametrami b<0 i a 0 to wtedy:

jest parametrycznym równaniem krzywej stożkowej leżącej w płaszczyźnie xy,
której ognisko leży w barycentrum układu. Uogólniając to na n ciał, w ruchu
homograficznym płaskim każde z ciał porusza się po krzywej stożkowej, a
jednocześnie wielobok utworzony przez nie zachowuje swój kształt.

przykład

0

a

m

a

m

2

2

1

1

a

m

a

a

m

a

1

2

2

1

3

2

2

1

a

1

m

m

1

b

)

t

(

aq

p

iy

x

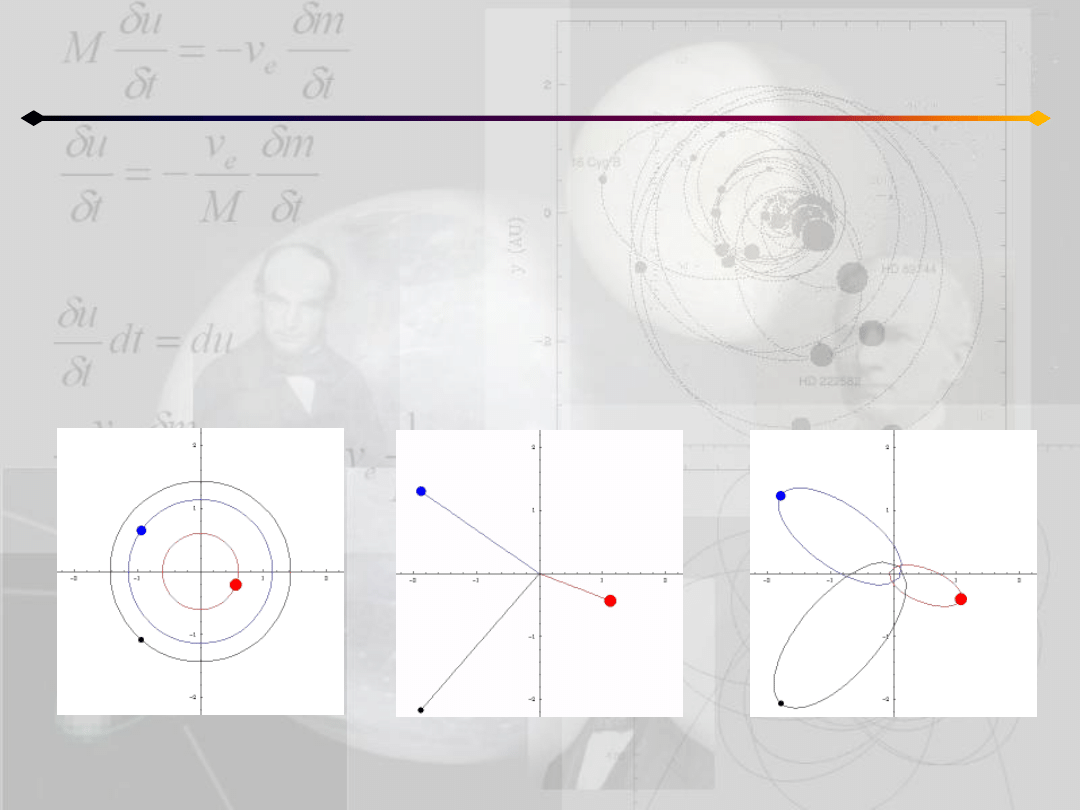
Zagadnienie n ciał

Ruch homograficzny – podsumowanie

1. Każdy ruch homograficzny (w szczególności współliniowy) jest płaski jeśli

całkowity moment pędu jest różny od 0

2. Kiedy całkowity moment pędu znika mamy do czynienia z ruchem

jednokładnym

3. Ruch homograficzny z zerowym momentem pędu jest ruchem jednokładnym

gdzie każde z ciał porusza się po prostej przechodzącej przez barycentrum

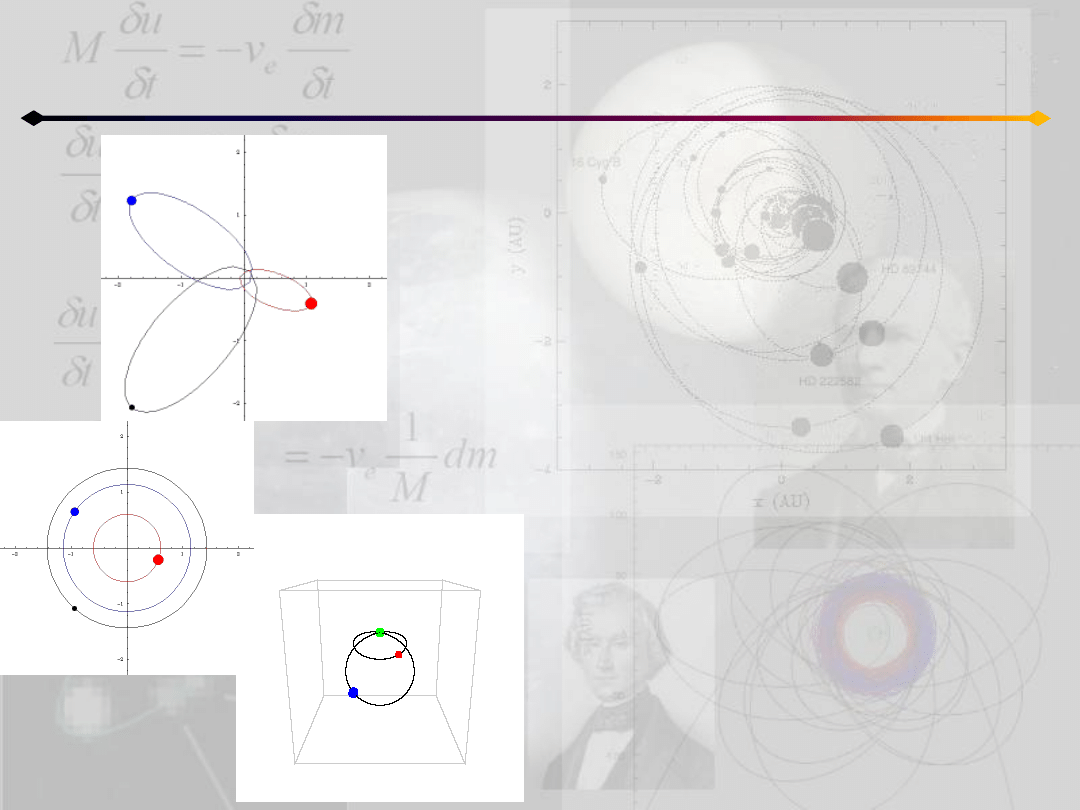
Zagadnienie 3 ciał

Zagadnienie trzech ciał (a także każdej innej
ich liczby) polega na wyznaczeniu ich ruchu
przy znanych warunkach początkowych
(położenie i prędkości).

Poza tym zakładamy, że ciała działają na siebie
tylko siłą grawitacji i poruszają się w pustej
przestrzeni

W ogólnym przypadku nie jest rozwiązywalne

Istnieje kilka rozwiązao szczególnych:

1. współliniowe
2. homograficzne
3. ruch po ósemce

Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Dla n=3 równania ruchu przyjmują postad:

Jest to układ rzędu 18-tego i może byd zredukowany do układu rzędu 6-tego, który
jest klasycznym problemem 3 ciał.

Taki układ ma rozwiązania szczególne (homograficzne) podane przez Lagrange’a.

3

2

3

23

3

2

3

1

3

13

3

1

3

3

2

1

3

12

2

1

2

3

3

32

2

3

2

2

1

3

3

31

1

3

1

2

3

21

1

2

1

1

r

r

r

m

Gm

r

r

r

m

Gm

r

m

r

r

r

m

Gm

r

r

r

m

Gm

r

m

r

r

r

m

Gm

r

r

r

m

Gm

r

m





































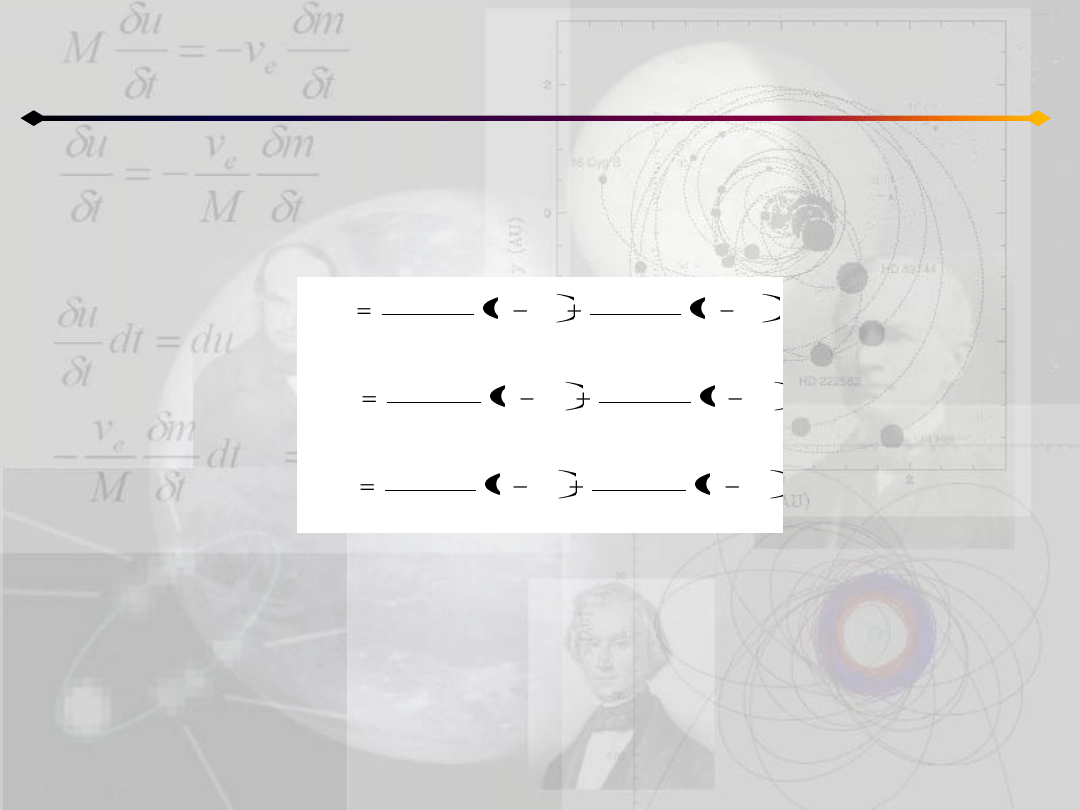
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Zacznijmy od przypadku homograficznego współliniowego. Warunki determinujące
ruch homograficzny:

w przypadku trzech ciał przyjmują postad:

n

,...,

2

,

1

k

,

j

0

x

r

x

x

m

X

o

j

2

j

k

3

o

jk

o

j

o

k

k

j

0

x

r

x

x

m

r

x

x

m

0

x

r

x

x

m

r

x

x

m

0

x

r

x

x

m

r

x

x

m

o

3

2

3

o

32

o

3

o

2

2

3

o

31

o

3

o

1

1

o

2

2

3

o

21

o

2

o

1

1

3

o

23

o

2

o

3

3

o

1

2

3

o

13

o

1

o

3

3

3

o

12

o

1

o

2

2

(11.4)

Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Spośród uzyskanych równao jedynie dwa są niezależne, ponieważ współrzędne x

i

o

odnoszą się do barycentrum. Możemy założyd, że:

wtedy:

Odejmując od siebie pierwsze dwa równania układu (11.4) otrzymujemy:

a po odjęciu ostatnich dwóch:

o

3

o

2

o

1

x

x

x

o

2

o

3

o

32

o

23

o

1

o

3

o

31

o

13

o

1

o

2

o

21

o

12

x

x

r

r

,

x

x

r

r

,

x

x

r

r

2

o

23

2

o

13

3

2

o

12

2

1

o

12

2

r

1

r

1

m

r

m

m

r

2

o

12

2

o

13

1

2

o

23

3

2

o

12

2

r

1

r

1

m

r

m

m

r

(11.5)

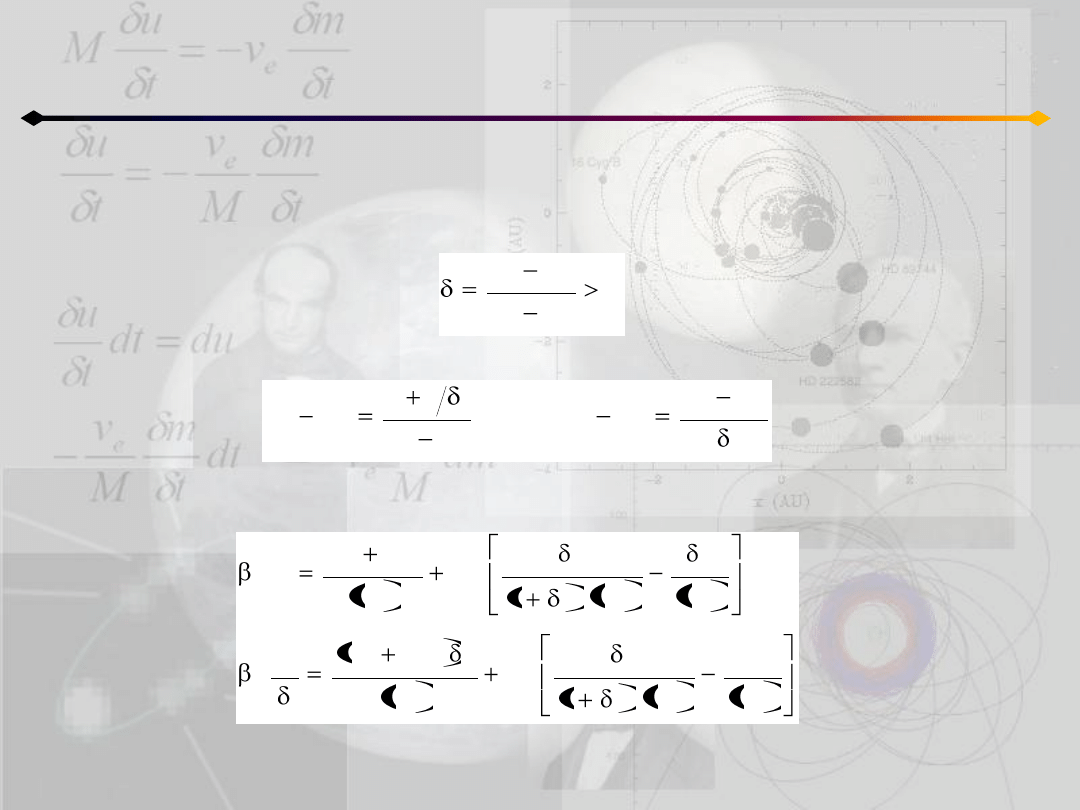
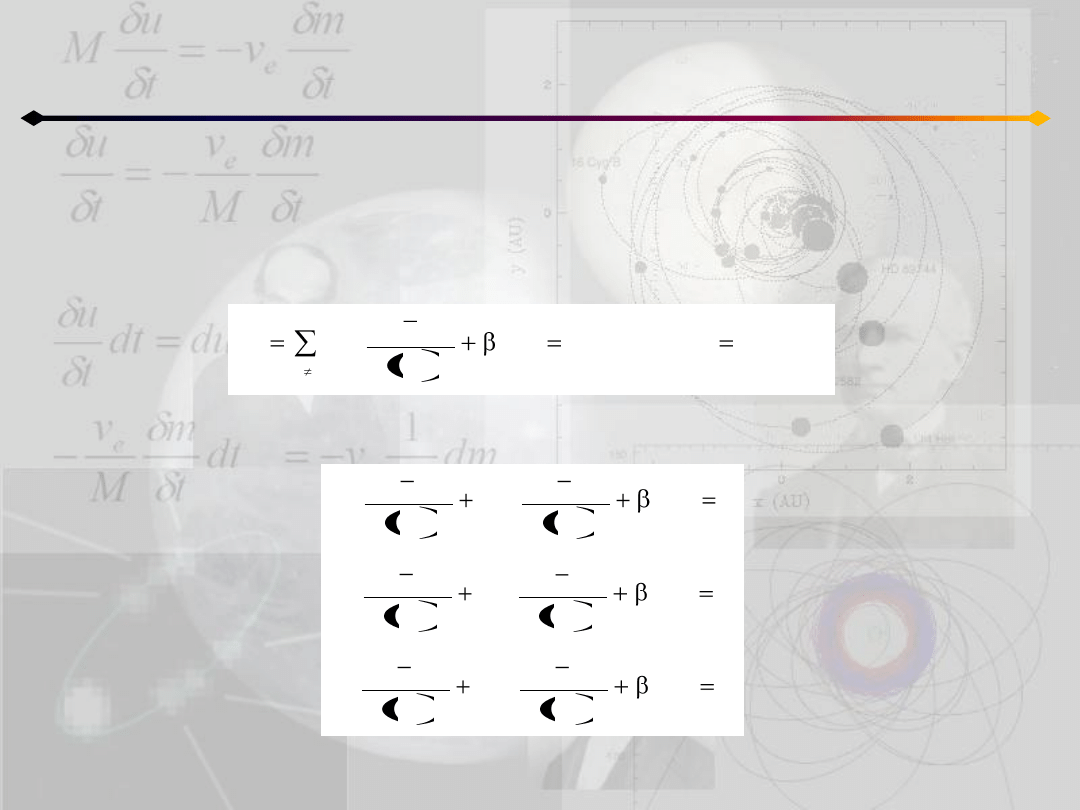
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Następnie zdefiniujmy:

skąd mamy:

co pozwala zapisad równania 11.5 w postaci:

0

x

x

x

x

o

2

o

3

o

1

o

2

o

1

o

2

o

2

o

3

o

1

o

2

o

1

o

3

x

x

x

x

x

x

1

1

x

x

2

o

12

2

o

12

2

2

1

2

o

12

2

3

1

o

12

2

2

o

12

2

2

o

12

2

2

3

2

o

12

2

1

o

12

2

r

1

r

1

m

r

m

m

r

r

r

1

m

r

m

m

r

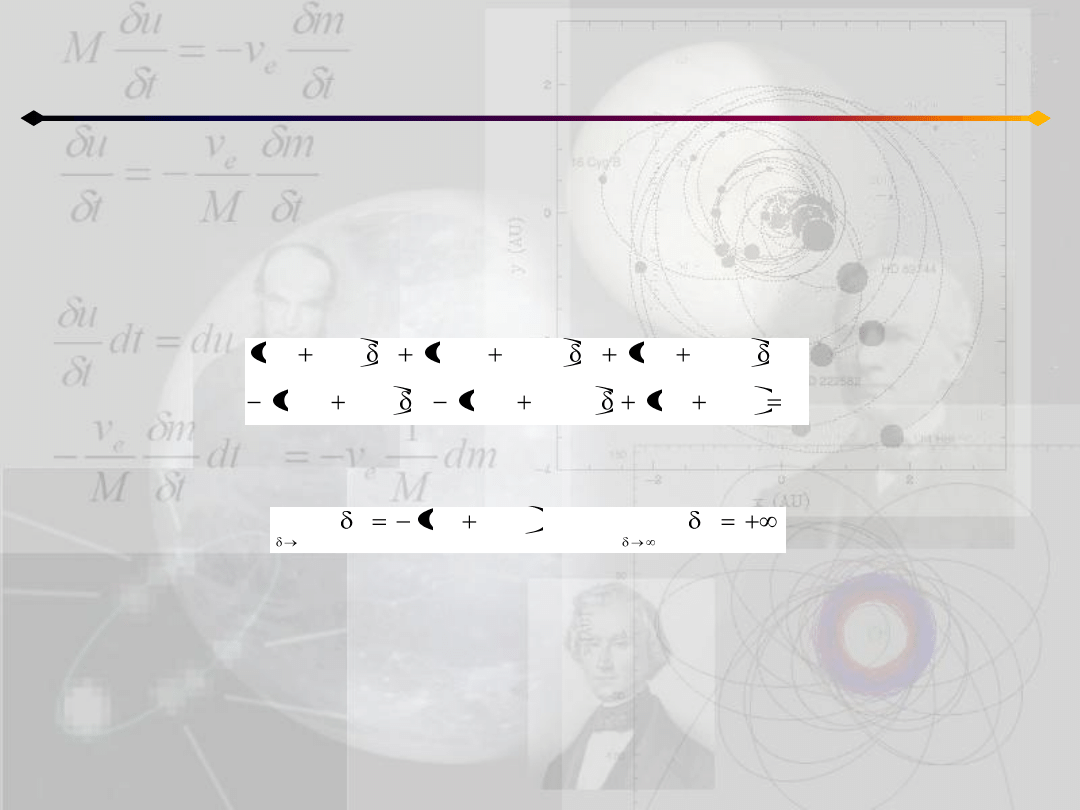
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Eliminując, z otrzymanych równao, r

12

o

dostajemy wielomian piątego stopnia

w postaci:

jeśli wszystkie wyrazy zawierające δ zastąpimy przez f(δ) to:

co oznacza, że otrzymany wielomian ma co najmniej jeden pierwiastek rzeczywisty.

0

m

m

m

2

m

3

m

m

3

m

3

m

m

3

m

2

m

m

2

1

2

1

2

2

1

3

3

2

4

3

2

5

3

2

)

(

f

lim

m

m

)

(

f

lim

2

1

0

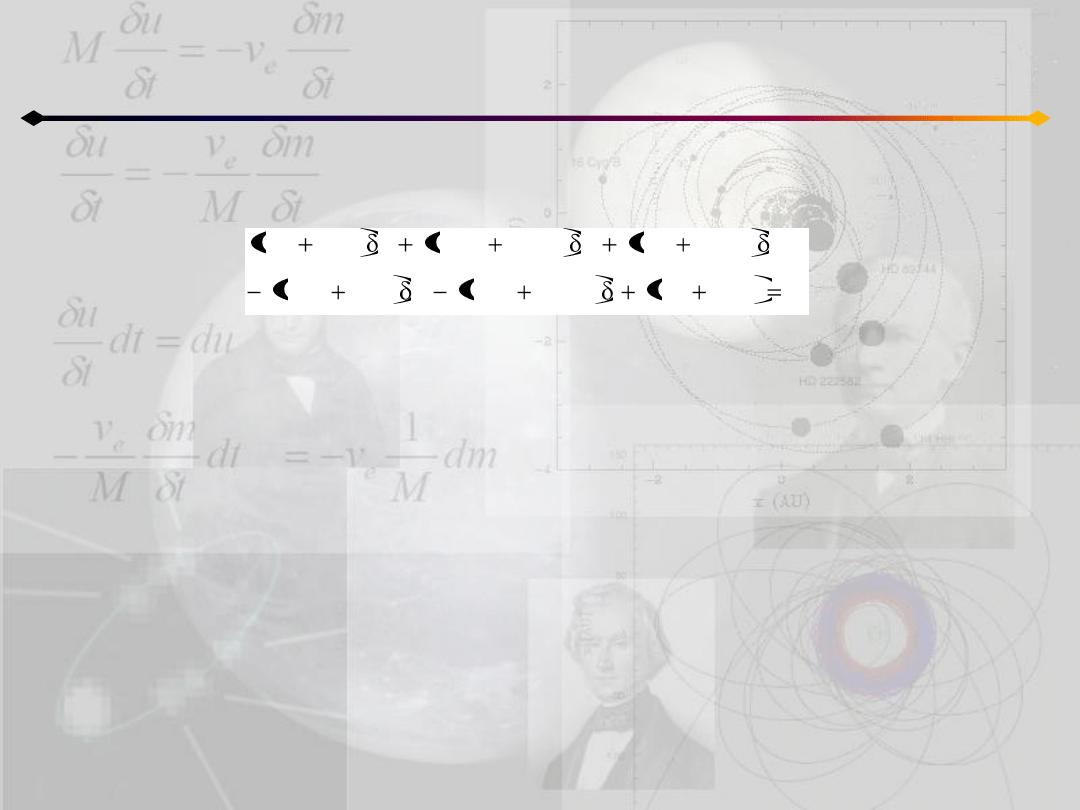
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Można pokazad, że jest to tylko jeden pierwiastek. Wynika to z reguły Kartezjusza:

„liczba dodatnich pierwiastków wielomianu jest równa liczbie zmian znaku pomiędzy
kolejnymi niezerowymi współczynnikami lub też mniejsza od niej o wielokrotnośd
liczby 2; liczbę ujemnych pierwiastków można oszacowad zamieniając x na − x”

Ponieważ są trzy możliwości rozłożenia trzech punktów na linii prostej więc istnieją
trzy rozwiązania współliniowe.

Dla λ=const wszystkie ciała rotują ze stałą prędkością kątową i mamy przypadek
równowagi względnej

Gdy λ nie jest stałe to wszystkie ciała zakreślają krzywe stożkowe o wspólnym ognisku

0

m

m

m

2

m

3

m

m

3

m

3

m

m

3

m

2

m

m

2

1

2

1

2

2

1

3

3

2

4

3

2

5

3

2

Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Wródmy do układu 11.3b i rozpatrzmy przypadek jednopłaszczyznowy:

gdzie niewiadomymi są stałe zespolone a

k

(k=1,2,3), które razem z

funkcją q(t) określają położenia mas m

1

, m

2

, m

3

na płaszczyźnie zespolonej.

Dla t=0 możemy unormowad funkcję q(t) biorąc częśd rzeczywistą za równą 1, a
częśd urojoną równą 0 (wtedy q(0)=1). Dodatkowo:

Wtedy układ 11.3b uzupełniony o warunek jaki spełniad mają współrzędne
barycentryczne, przyjmuje postad:

k

l

3

k

l

k

l

l

k

a

a

a

a

m

G

b

a

o

3

o

3

3

o

2

o

2

2

o

1

o

1

1

iy

x

a

iy

x

a

iy

x

a

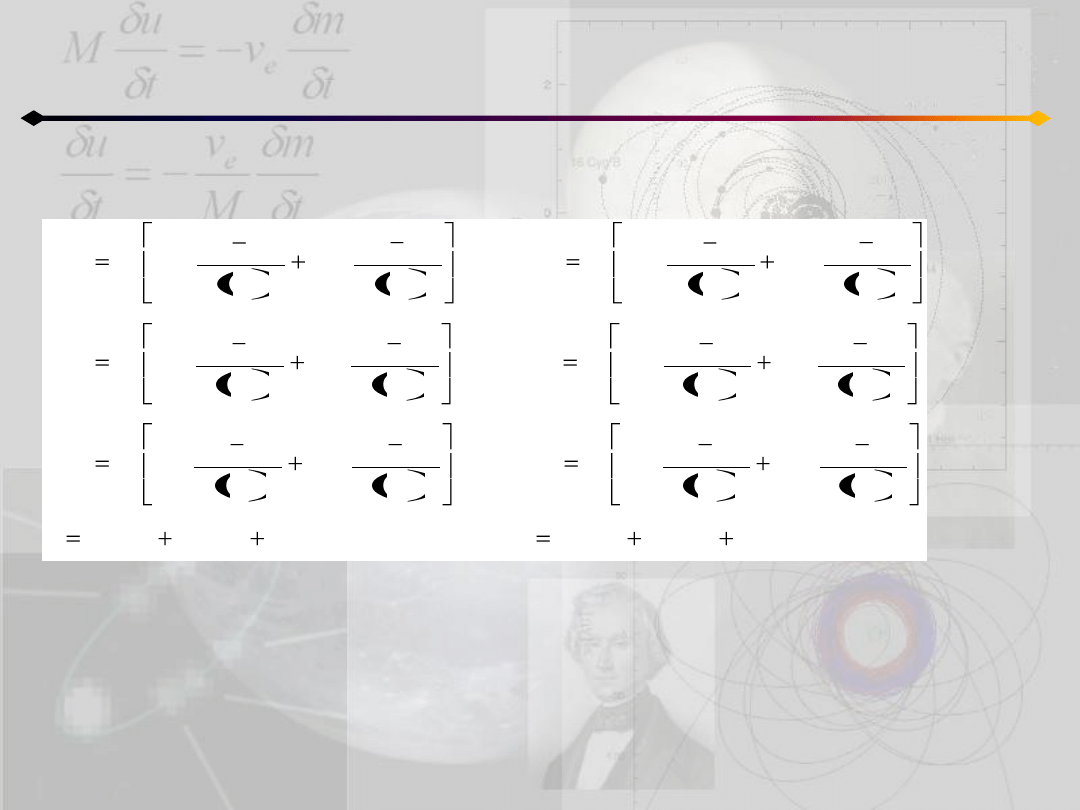
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

o

3

3

o

2

2

o

1

1

o

3

3

o

2

2

o

1

1

3

o

32

o

3

o

2

2

3

o

31

o

3

o

1

1

o

3

3

o

32

o

3

o

2

2

3

o

31

o

3

o

1

1

o

3

3

o

21

o

2

o

1

1

3

o

23

o

2

o

3

3

o

2

3

o

21

o

2

o

1

1

3

o

23

o

2

o

3

3

o

2

3

o

13

o

1

o

3

3

3

o

12

o

1

o

2

2

o

1

3

o

13

o

1

o

3

3

3

o

12

o

1

o

2

2

o

1

y

m

y

m

y

m

0

x

m

x

m

x

m

0

r

y

y

m

r

y

y

m

G

b

y

r

x

x

m

r

x

x

m

G

b

x

r

y

y

m

r

y

y

m

G

b

y

r

x

x

m

r

x

x

m

G

b

x

r

y

y

m

r

y

y

m

G

b

y

r

x

x

m

r

x

x

m

G

b

x

(11.6)

W tym układzie tylko sześd równao jest niezależnych. Równania współrzędnych
barycentrycznych mogą byd uzyskane po pomnożeniu pozostałych sześciu przez
odpowiednie masy i dodaniu do siebie.

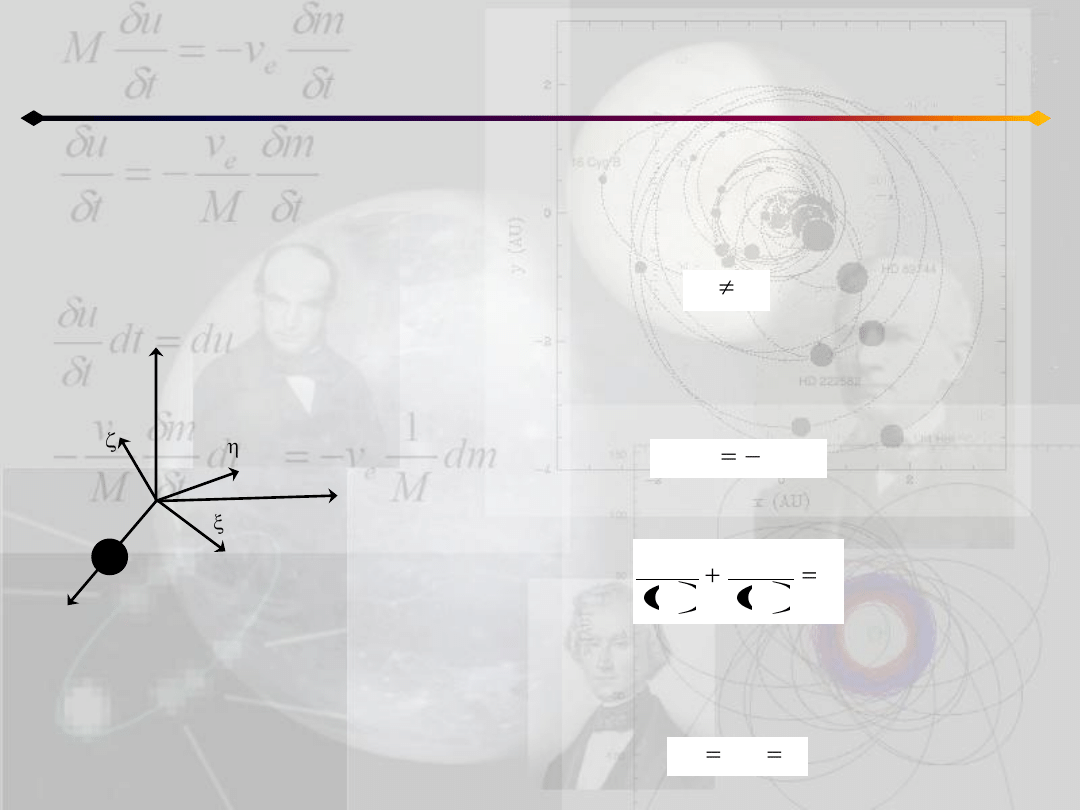
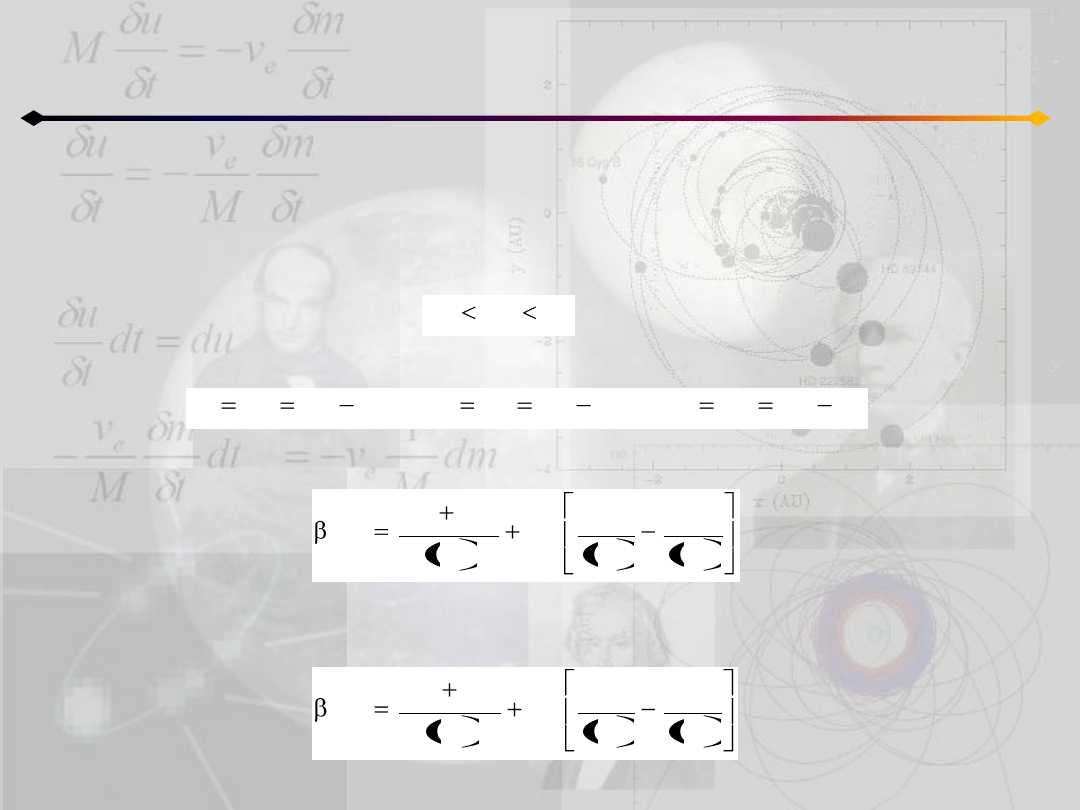
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Aby uzyskad rozwiązania Lagrange’a załóżmy na początek,
że nie mamy do czynienia z przypadkiem równobocznym,
czyli:

Orientacja osi układu jest dowolna. W takim razie
możemy wybrad oś x tak, aby przechodziła przez masę
m

3

. Wtedy y

3

o

=0 i z równania barycentrum mamy:

jednocześnie z innego z równao układu 11.6 dostajemy:

Powyższe równania są spełnione równocześnie tylko w
przypadku (pamietając o tym, że zakładaliśmy nierówne
boki):

o

23

o

13

r

r

o

2

2

o

1

1

y

m

y

m

0

r

y

m

r

y

m

3

o

32

o

2

2

3

o

31

o

1

1

0

y

y

o

2

o

1

z

y

x

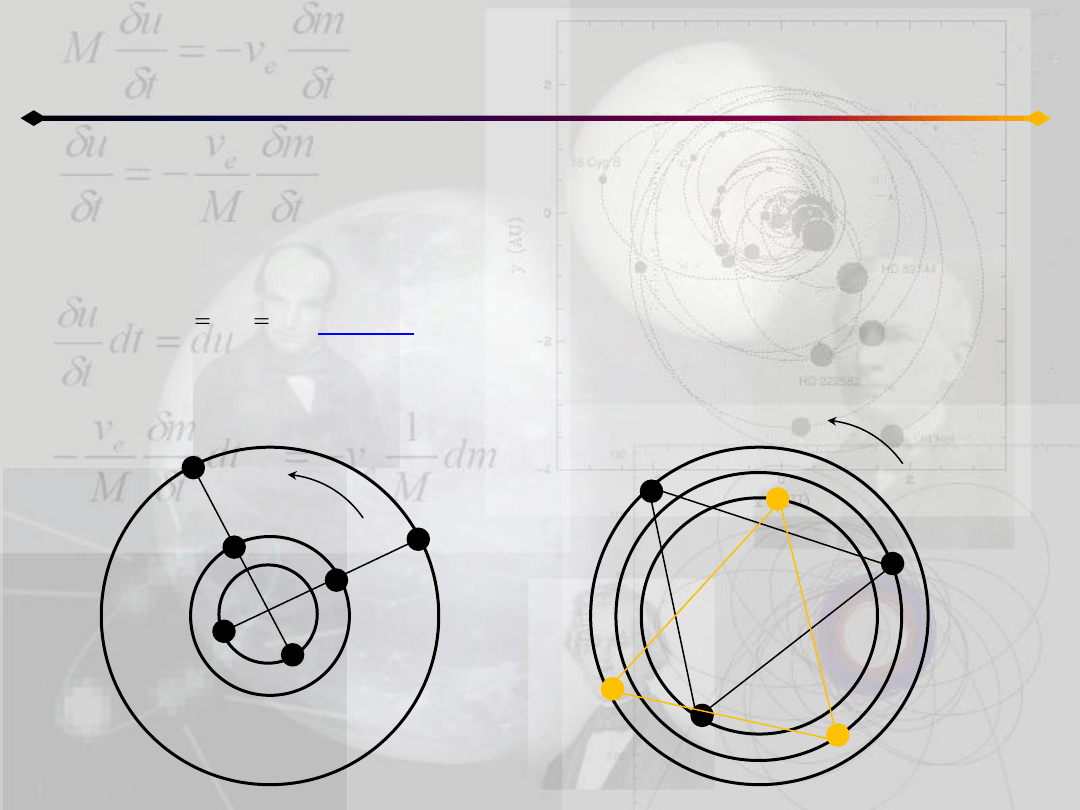
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Powtarzając tą procedurę dla osi x przechodzącej przez pozostałe masy,
możemy pokazad, że jedynymi rozwiązaniami układu są:

1)

przykład

2) trzy masy leżące na jednej linii

o

31

o

23

o

13

r

r

r

ω

ω

Zagadnienie 3 ciał

Rozwiązania Lagrange’a

Rozwiązania Lagrange’a są jedynymi rozwiązaniami homograficznymi zagadnienia
trzech ciał. W takim wypadku w układzie 11.6 wstawiamy jedną wartośd odległości
między ciałami r

0

w momencie czasu t=0, wtedy:

podobnie dla pozostałych równao. Jeśli sumę mas oznaczymy przez M to:

3

0

o

3

3

2

1

o

3

3

0

o

2

3

2

1

o

2

3

0

o

1

3

2

1

3

0

o

3

3

o

2

2

o

1

3

o

1

2

o

1

r

x

m

m

m

G

b

x

r

x

m

m

m

G

b

x

r

x

m

m

m

G

r

x

m

x

m

x

m

x

m

G

b

x

3

0

r

GM

b

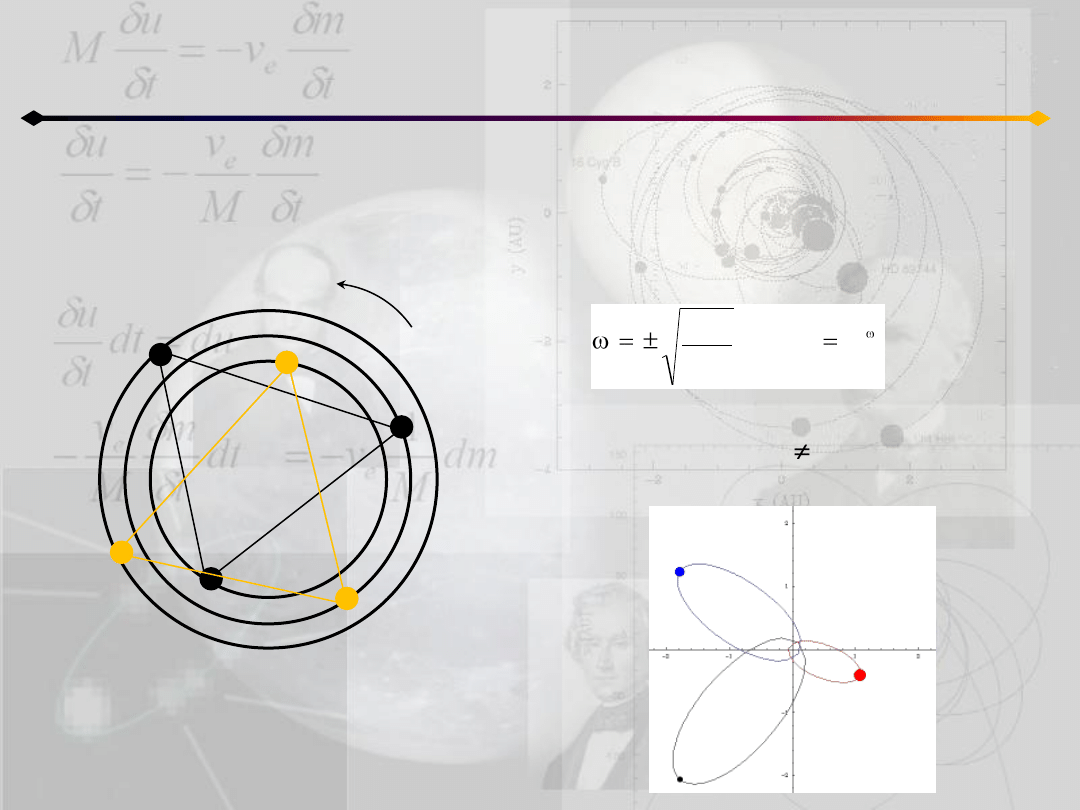
Zagadnienie 3 ciał

Rozwiązania Lagrange’a

ω

W przypadku orbit kołowych mamy –b=ω

2

,

gdzie ω jest wspólną prędkością kątową
wszystkich trzech ciał. Stąd:

W ogólnym przypadku (λ const) orbity są
krzywymi stożkowymi. Dla orbit eliptycznych:

t

i

3

0

e

q

,

r

GM