
Wykład czwarty
Pochodna funkcji
Zał. Funkcja f jest określona w pewnym otoczeniu O punktu x
0
; ∆x 6= 0 – przyrost argumentu
x taki, że x
0
+ ∆x ∈ O.
Ułamek:
f (x
0
+ ∆x) − f (x
0
)
∆x
nazywamy
ilorazem różnicowym
.
Definicja 1. Liczbę lim
∆x→0
f (x
0
+ ∆x) − f (x
0
)
∆x
nazywamy
pochodną funkcji f w punkcie
x
0
i
oznaczamy przez f
0
(x
0
).
Pochodne jednostronne (obliczane przy pomocy odpowiednich granic jednostronnych) funkcji f
oznaczamy przez: f
0
(x
−
0
) , f
0
(x
+
0
).
Funkcję f
0
nazywamy
pochodną funkcji
f .
Interpretacja geometryczna pochodnej
Równanie siecznej wykresu f przechodzącej przez punkty (x
0
, f (x
0
)), (x
0
+ ∆x, f (x
0
+ ∆x)) ma
postać: y − f (x
0
) =
f (x
0
+ ∆x) − f (x
0
)
∆x
· (x − x
0
).
Granicznym położeniem tej siecznej (∆x → 0) jest styczna do wykresu funkcji f w punkcie
(x
0
, f (x
0
)). Jeśli f
0
(x
0
) istnieje, to równanie tej stycznej:
y − f (x
0
) = f
0
(x
0
) · (x − x
0
)
Α
Hx
0
, f
Hx
0
LL
Hx
0
+ Dx, f
Hx
0
+ Dx
LL
Α
Dx
y = f
HxL
sieczna
styczna
-1
1
2
3
4
X
0.5
1.0
1.5
2.0
2.5
3.0
Y
Uwaga 1. Jeżeli lim
∆x→0
f (x
0
+ ∆x) − f (x
0
)
∆x
jest niewłaściwa, to styczną do wykresu f w punkcie
(x
0
, f (x
0
)) jest prosta x = x
0
.
1

styczna do wykresu
w punkcie (1,0)
0.5
1.0
1.5
X
-1.0
-0.5
0.5
Y
Obliczanie pochodnych
Twierdzenie 1. (o działaniach arytmetycznych na pochodnych)Jeżeli funkcje f i g po-
siadają pochodne f
0
, g
0
, to prawdziwe są wzory
1. (α · f )
0
= α · f
0
dla każdej liczby rzeczywistej α
2. (f + g)
0
= f
0
+ g
0
3. (f − g)
0
= f
0
− g
0
4. (f · g)
0
= f
0
· g + f · g
0
5.
f
g
!
0
=
f
0
· g − g
0
· f
g
2
, g 6= 0
Pochodne funkcji elementarnych
1. (c)
0
= 0
c – funkcja stała
2. (x
n
)
0
= nx
n−1
, n ∈ N
3. (sin x)
0
= cos x
4. (cos x)
0
= − sin x
5. (tg x)
0
=
1
cos
2
x
= 1 + tg
2
x
6. (ctg x)
0
= −
1
sin
2
x
7. (a
x
)
0
= a
x
· ln a ; (e
x
)
0
= e
x
Twierdzenie 2. (o pochodnej funkcji odwrotnej) Jeżeli funkcja f jest ściśle monotoniczna
i posiada pochodną f
0
(x) 6= 0, to funkcja odwrotna f
−1
posiada pochodną i prawdziwy jest wzór
2
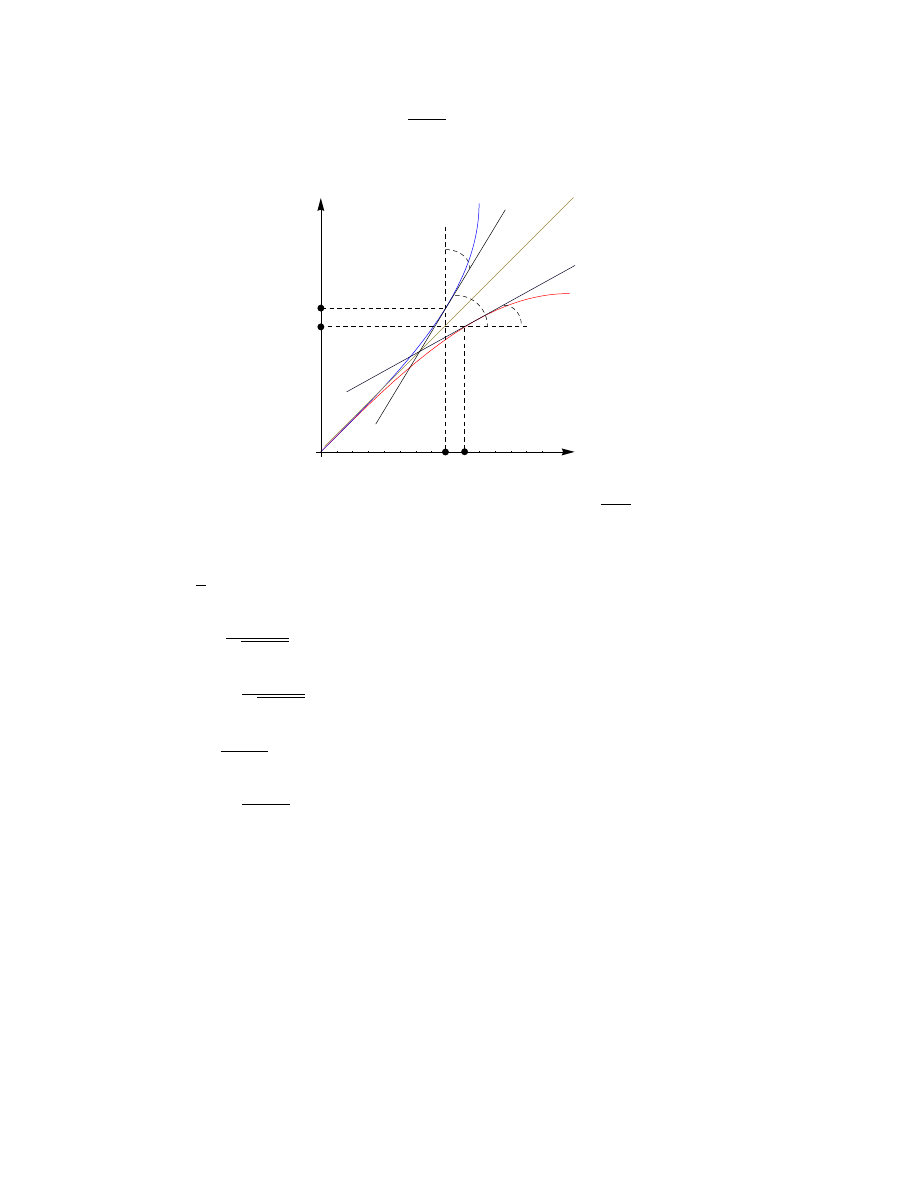
(f
−1
(y))
0
=
1
f
0
(x)
, gdzie y = f (x)
Α
Α
Β
y = g
HxL
y = x
y = f
HxL
x
0
y
0
y
0
x
0
0.5
1.0
X
0.5
1.0
Y
f
0
(x
0
) = tg α, g
0
(y
0
) = tg β, tg β = ctg α =
1
tg α
8. (ln x)
0
=
1
x
9. (arcsin x)
0
=
1
√
1 − x
2
10. (arccos x)
0
= −
1
√
1 − x
2
11. (arctg x)
0
=
1
x
2
+ 1
12. (arcctg x)
0
= −
1
x
2
+ 1
Twierdzenie 3. (o pochodnej funkcji złożonej) Jeżeli funkcja f ma pochodną w punkcie x
i funkcja g ma pochodną w punkcie y = f (x), to funkcja złożona g ◦ f ma pochodną w punkcie
x i prawdziwy jest wzór
(g ◦ f )
0
(x) = g
0
(f (x)) · f
0
(x)
Powyższy wzór można stosować wielokrotnie.
13. (sh x)
0
= ch x
14. (ch x)
0
= sh x
15. (x
α
)
0
= α · x
α−1
, α ∈ R − {0}
3
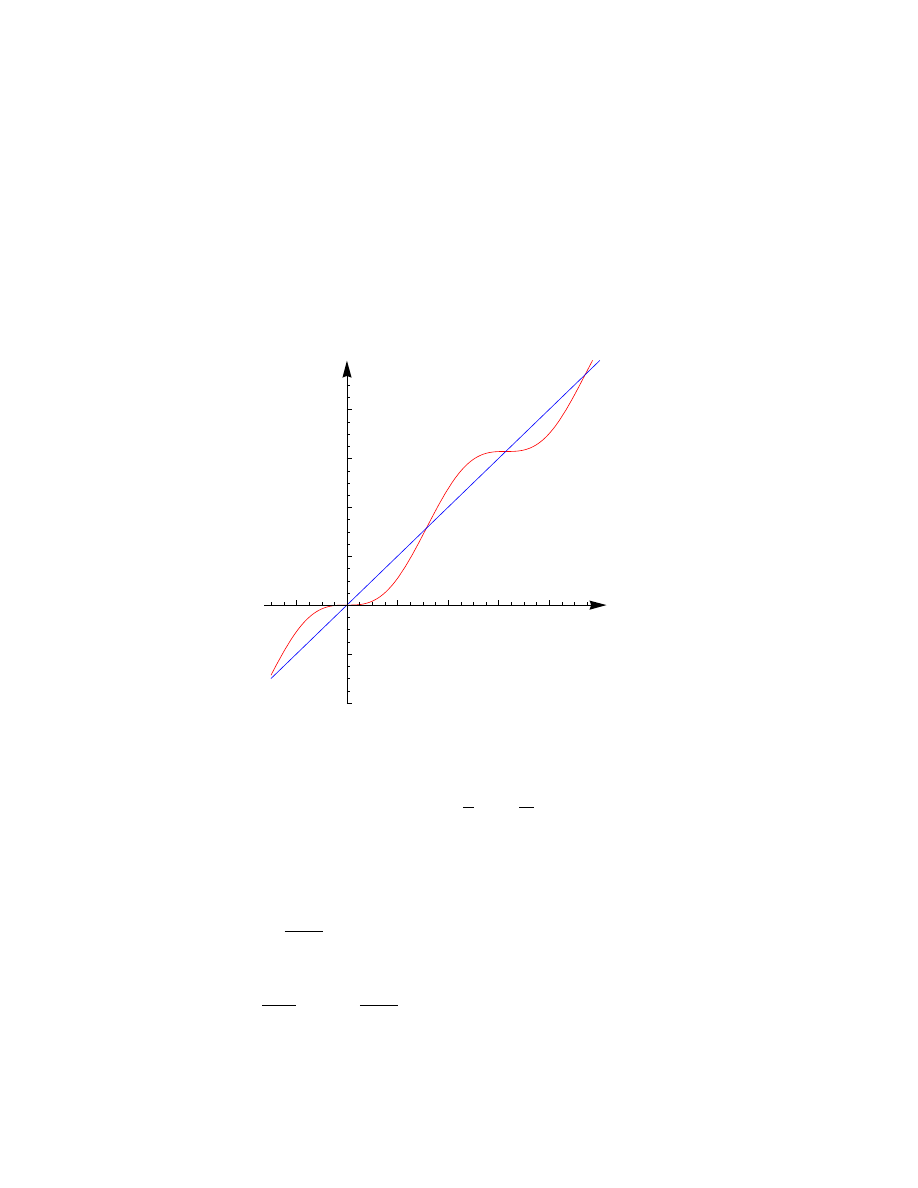
Twierdzenie 4. (WK istnienia pochodnej)Jeżeli f
0
(x
0
) istnieje, to funkcja f jest ciągła w
punkcie x
0
.
Uwaga 2. Jeżeli istnieje pochodna f
0
w przedziale P , to
1. jeżeli funkcja f jest rosnąca na przedziale P , to f
0
0 na tym przedziale;
2. jeżeli funkcja f jest malejąca na przedziale P , to f
0
¬ 0 na tym przedziale.
y = x
y = x - sinx
-2
2
4
6
8
X
-4
-2
2
4
6
8
Y
Funkcja f (x) = x − sin x jest rosnąca w R. f
0
(x) = 0 dla nieskończenie wielu x ∈ R.
Twierdzenie 5. (de l’Hospitala) Jeżeli funkcje
f
h
oraz
f
0
h
0
są określone na pewnym sąsiedztwie
punktu x
0
oraz
1. lim
x→x
0
f (x) = lim
x→x
0
h(x) = 0 lub | lim
x→x
0
h(x)| = +∞ ;
2. istnieje granica lim
x→x
0
f
0
(x)
h
0
(x)
(właściwa lub niewłaściwa)
to istnieje granica lim
x→x
0
f (x)
h(x)
= lim
x→x
0
f
0
(x)
h
0
(x)
.
4
Wyszukiwarka
Podobne podstrony:
anl1 w02 zima2012 id 65272 Nieznany (2)
anl1 w01 zima2012 id 65270 Nieznany (2)
al1 w04 zima2011 id 54566 Nieznany (2)
anl1 w04 lato2009 id 65274 Nieznany (2)
anl1 w05 zima2012 id 65276 Nieznany (2)
anl1 w03 zima2012 id 65273 Nieznany (2)
al1 w07 zima2011 id 54569 Nieznany (2)
anl1 w02 lato2009 id 65271 Nieznany (2)
al1 w08 zima2011 id 54571 Nieznany (2)
MM ETK W04 zmiennestanu id 3442 Nieznany
DSaA W04 Techniques id 143853 Nieznany
al1 w05 zima2011 id 54567 Nieznany (2)
al1 w06 zima2011 id 54568 Nieznany (2)
M W04 57 id 274844 Nieznany
gs w04 id 197501 Nieznany
krs form w04 id 251003 Nieznany
gs w04 id 197501 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
więcej podobnych podstron