MODELOWANIE I SYMULACJA

Wyprowadzanie równań różniczkowych ruchu prostych układów mechanicznych

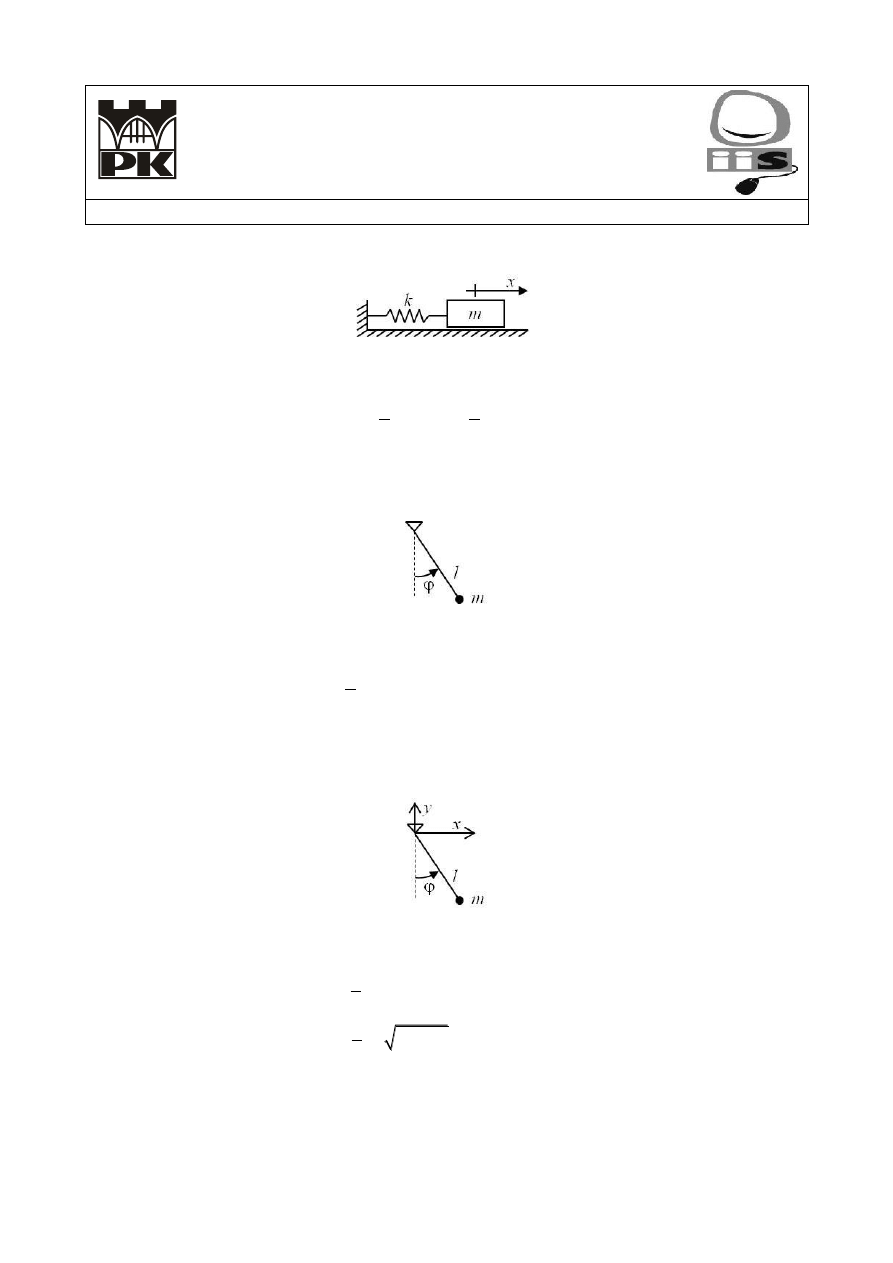
Zadanie 1.

Wyprowadzić równanie różniczkowe opisujące ruch oscylatora harmonicznego wiedząc, że energia
kinetyczna i potencjalna określone są wzorami

2

2

1

1

,

2

2

E

mv

U

kx





gdzie m i k oznaczają odpowiednio masę oscylatora i współczynnik sprężystości.
Rozwiązać otrzymane równanie dla dowolnych warunków początkowych.

Zadanie 2.

Wyprowadzić równanie różniczkowe opisujące ruch wahadła matematycznego wiedząc, że energia
kinetyczna i potencjalna określone są wzorami

2

2

1

,

cos( )

2

E

ml

U

mgl





 



gdzie m oznacza masę, l – długość wahadła, g – przyspieszenie ziemskie.
Rozwiązać otrzymane równanie dla dowolnych warunków początkowych.

Zadanie 3.

Wyprowadzić równania różniczkowe opisujące ruch wahadła matematycznego zawieszonego na
elastycznej lince wiedząc, że energia kinetyczna i potencjalna określone są wzorami









2

2

2

2

2

1

2

1

2

x

y

E

m v

v

U

k

x

y

l

mgy













gdzie m oznacza masę, l – długość wahadła, g – przyspieszenie ziemskie, k – współczynnik
sprężystości.

Zadanie 4.

Wyprowadzić równania różniczkowe opisujące ruch wahadła matematycznego podwieszonego na
oscylatorze wiedząc, że energia kinetyczna i potencjalna określone są wzorami





2

2

2

2

1 1

2

1

1 2

2

2

2

1

2

2

1

1

2

cos(

)

2

2

1

cos(

)

2

E

m v

m v

v v l

x

l v

U

kx

m gl

x













gdzie m

1

oznacza masę oscylatora, m

2

– masę wahadła, l – długość wahadła, g – przyspieszenie

ziemskie, k – współczynnik sprężystości sprężyny.

Wyznaczyć rozwiązanie układu równania za pomocą komendy dsolve z opcją numeric
przyjmując następujące dane: m

1

= 1, m

2

= 0.1, g = 9.81, l = 0.1, k = 100 i warunki początkowe:

1

1

2

2

(0)

0.5 , (0)

0,

(0)

,

(0)

0.

3

x

l v

x

v













Dokonać animacji ruchu wahadła korzystając z komend

> X:=t->'rhs(roz(t)[2])';Y:=t->'rhs(roz(t)[4])';
> a1:=animate(pointplot,[[X(t),0],symbol=box,symbolsize=30],
t=0..5,frames=200,color=blue,color=red):
> a2:=animate(pointplot,[[X(t)+l*sin(Y(t)),-l*cos(Y(t))],
symbol=circle,symbolsize=30],t=0..5,frames=200,color=blue,
color=red):
> a3:=animate(plot,[[[X(t),0],
[X(t)+l*sin(Y(t)),-l*cos(Y(t))]]],t=0..5,axes=none,
scaling=constrained,thickness=2,frames=200):
> display(a1,a2,a3);

>

restart:

>

with(plots):

>

lagrange := proc (n, q, r, L) local i, uzm_q, uzm_r, rel_r_q, Lq,

Lr, Lrt; global row; uzm_q := seq(q[i] = q[i](t), i = 1 .. n); uzm_r
:= seq(r[i] = r[i](t), i = 1 .. n); for i to n do Lq[i] := subs([uzm_q,
uzm_r], diff(L, q[i])); Lr[i] := subs([uzm_q, uzm_r], diff(L, r[i]))
end do; for i to n do Lrt[i] := diff(Lr[i], t) end do; rel_r_q :=
seq(r[i](t) = diff(q[i](t), t), i = 1 .. n); for i to n do row[i] :=
subs(rel_r_q, Lrt[i]-Lq[i] = 0) end do; seq(row[i], i = 1 .. n) end
proc:

>
>

#Zad1

>

E := (1/2)*m*v[1]^2:

>

U := (1/2)*k*x^2:

>

L := E-U:

>

lagrange(1, x, v, L):

>
>

#Zad2

>

restart:

>

E := (1/2)*m*l^2*omega[1]^2:

>

U := -m*g*l*cos(phi[1]):

>

L := E-U:

>

lagrange(1, phi, omega, L):

>
>

#Zad3

>

restart:

>

E := (1/2)*m*(v[1]^2+v[2]^2):

>

U := (1/2)*k*(sqrt(x[1]^2+x[2]^2)-l)^2+m*g*x[2]:

>

L := E-U:

>

lagrange(2, v, x, L):

>
>

#Zad4

>

restart:

>

E :=

(1/2)*m[1]*v[1]^2+(1/2)*m[2]*(v[1]^2+2*v[1]*v[2]*l*cos(x[2])+l^2*
v[2]^2):

>

U := (1/2)*k*x[1]^2-m[2]*g*l*cos(x[2]):

>

m[1] := 1: m[2] := .1: g := 9.81: l := .1: k := 100:

>

wp := x[1](0) = .5*l, (D(x[1]))(0) = 0, x[2](0) = (1/3)*Pi,

(D(x[2]))(0) = 0:

>

L := E-U:

>

lagrange(2, x, v, L):

>

dsolve({wp, row[1], row[2]}, {x[1](t), x[2](t)}, numeric):

MODELOWANIE I SYMULACJA

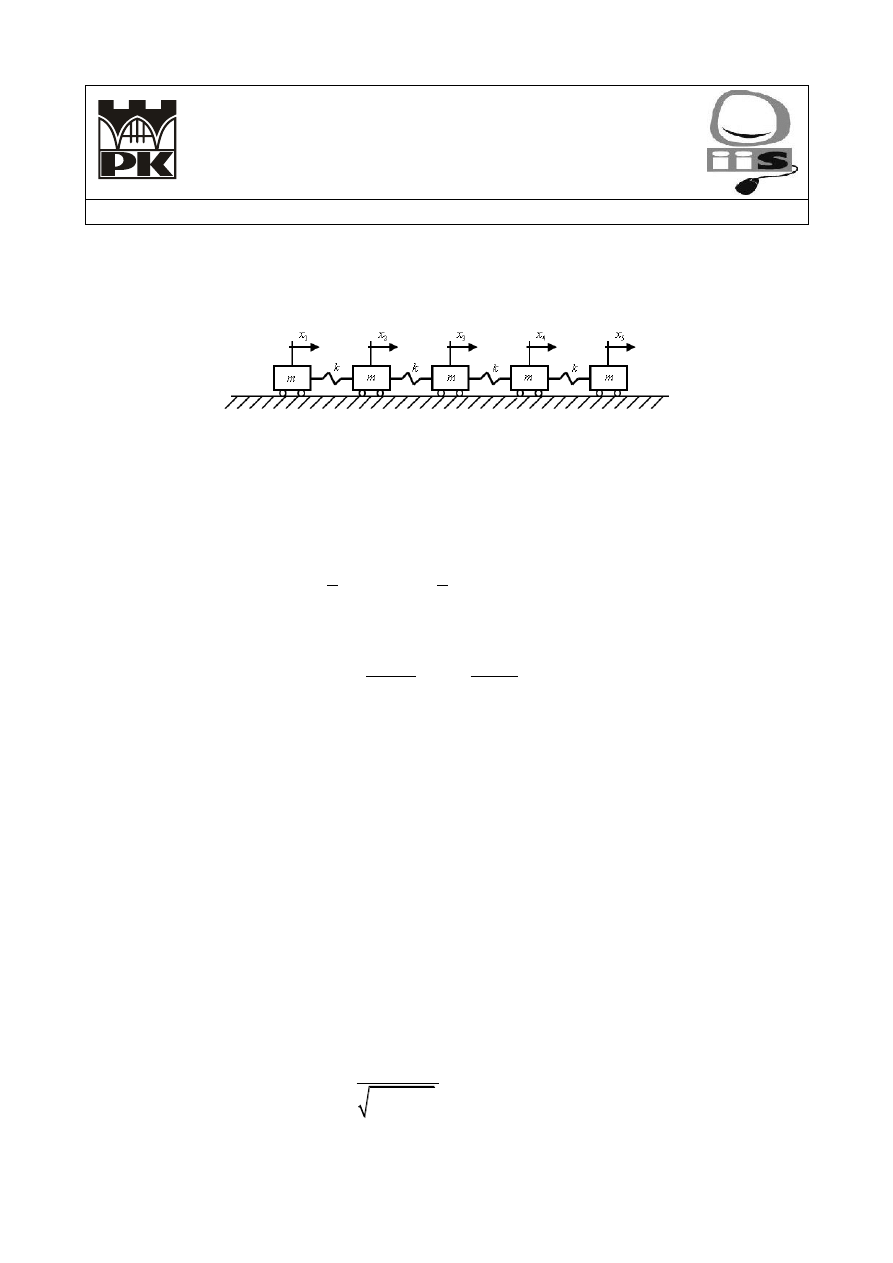
Modelowanie liniowego układu dyskretnego

Wyznaczyć rozwiązanie analityczne opisujące ruch liniowego układu dyskretnego przedstawionego
na rysunku

gdzie m oznacza masę poszczególnych ciał, k – sztywność każdej sprężyny, a x

i

, i = 1, 2, ...,5 –

przemieszczenia środków poszczególnych mas.

Kolejność postępowania:

1. Wyznaczyć energię kinetyczną i potencjalną układu wykorzystując zależności:

5

4

2

2

1

1

1

1

1

,

(

)

2

2

i

i

i

i

i

E

m

v

U

k

x

x

















2. Wyznaczyć macierz sztywności K i bezwładności M korzystając ze wzorów:

2

2

,

ij

ij

i

j

i

j

U

E

k

m

x x

v v









 

 

Uwaga: należy zadeklarować najpierw obie macierze, by następnie wyznaczyć ich elementy
w podwójne pętli

3. Wyznaczyć macierz A związaną z macierzami K i M wzorem





1

A

M K

4. Przyjąć dane liczbowe: m = 1, k = 100 i wyznaczyć wartości i wektory własne macierzy A

korzystając z komendy Eigenvectors w postaci

> alpha,V:=Eigenvectors(A):

5. Korzystając z procedury sortowanie posortować wartości własne zmieniając

równocześnie w odpowiedni sposób pozycje kolumn w macierzy V, zawierającej wektory
własne macierzy A

> alpha,V:=sortowanie(alpha,V);

6. Dokonać normalizacji wektorów własnych względem macierzy bezwładności korzystając ze

wzoru (u

i

– kolumny macierzy V)





,

1, 2,...,

i

i

T
i

i

i

n





u

w

u Mu

7. Wyznaczyć częstości drgań swobodnych korzystając z komendy map ze wzoru

,

1, 2,...,

i

i

i

n

  



gdzie



i

oznaczają posegregowane wartości własne.

8. Zadać warunki początkowe w formie wektora przemieszczeń początkowych x0

zawierającego zerowe elementy i wektora prędkości początkowych v0 zawierającego
niezerową pierwszą współrzędną równą 10

> x0:=Vector(5,[0,0,0,0,0]); v0:=Vector(5,[10,0,0,0,0]);

9. Wyznaczyć analityczne rozwiązanie opisujące ruch poszczególnych mas korzystając ze

wzoru

5

1

1

2

0

. .( 0

0 )

. .

0 cos (

)

sin (

)

T

T
i

i

i

i

i

i

t

t

t



















 





 































v

x

w M x

v

w

w M x

w

10. Sporządzić wykres przemieszeń i prędkości poszczególnych mas korzystając z poniższych

komend:

> plot([seq(x[i],i=1..n)],t=0..3);
> v:=map(diff,x,t):
> plot([seq(v[i],i=1..n)],t=0..3);

11. Dokonać animacji ruchu poszczególnych mas korzystając z poniższych komend:

> seq_pkt:=seq([(j-1)*3+'x'[j],0],j=1..n);
> animate(pointplot,[[seq_pkt],symbol=box,symbolsize=50],
t=0..3,frames=100,color=red,axes=none);

12. Sporządzić wykres czasowy energii mechanicznej (E + U)

> plot(E+U,t=0..5,0..100);

13. Która ze sprężyn będzie najbardziej ściśnięta/rozciągnięta w trakcie pierwszych trzech

sekund?

>

restart:

>

with(LinearAlgebra):

with(plots):

>

#sortowanie proc

>
>

#Zad1

>

E:=1/2*m*add(v[i]^2,i=1..5):

>

U:=1/2*k*add((x[i+1]-x[i])^2,i=1..4):

>
>

#Zad2

>

n:=5:

>

K:=Matrix(n):

>

M:=Matrix(n):

>

for i to n do

for j to n do
K[i,j]:=diff(U,x[i],x[j]);
M[i,j]:=diff(E,v[i],v[j]);
end do;
end do;

>

K:

>

M:

>
>

#Zad3

>

A:=1/M.K:

>
>

#Zad4

>

m:=1: k:=100:

>

alpha,V:=evalf(Eigenvectors(A)):

>
>

#Zad5

>

alpha,V:=sortowanie(alpha,V):

>
>

#Zad6

>

for i from 1 to n do

w[i]:=V[1..n,i]/(sqrt((V[1..n,i]^%T).M.V[1..n,i])):
end do:

>
>

#Zad7

>

for i from 1 to n do

omega[i]:=sqrt(alpha[i])
end do:

>
>

#Zad8

>

x0:=Vector(5,[0,0,0,0,0]):

>

v0:=Vector(5,[10,0,0,0,0]):

>
>

#Zad9

>

x:=(Transpose(w[1]).M.(x0+v0*t))*w[1]+add((Transpose(w[1]).M.(x0*cos(om
ega[i]*t)+v0*sin(omega[i]*t)/omega[i]))*w[i], i=2..5):