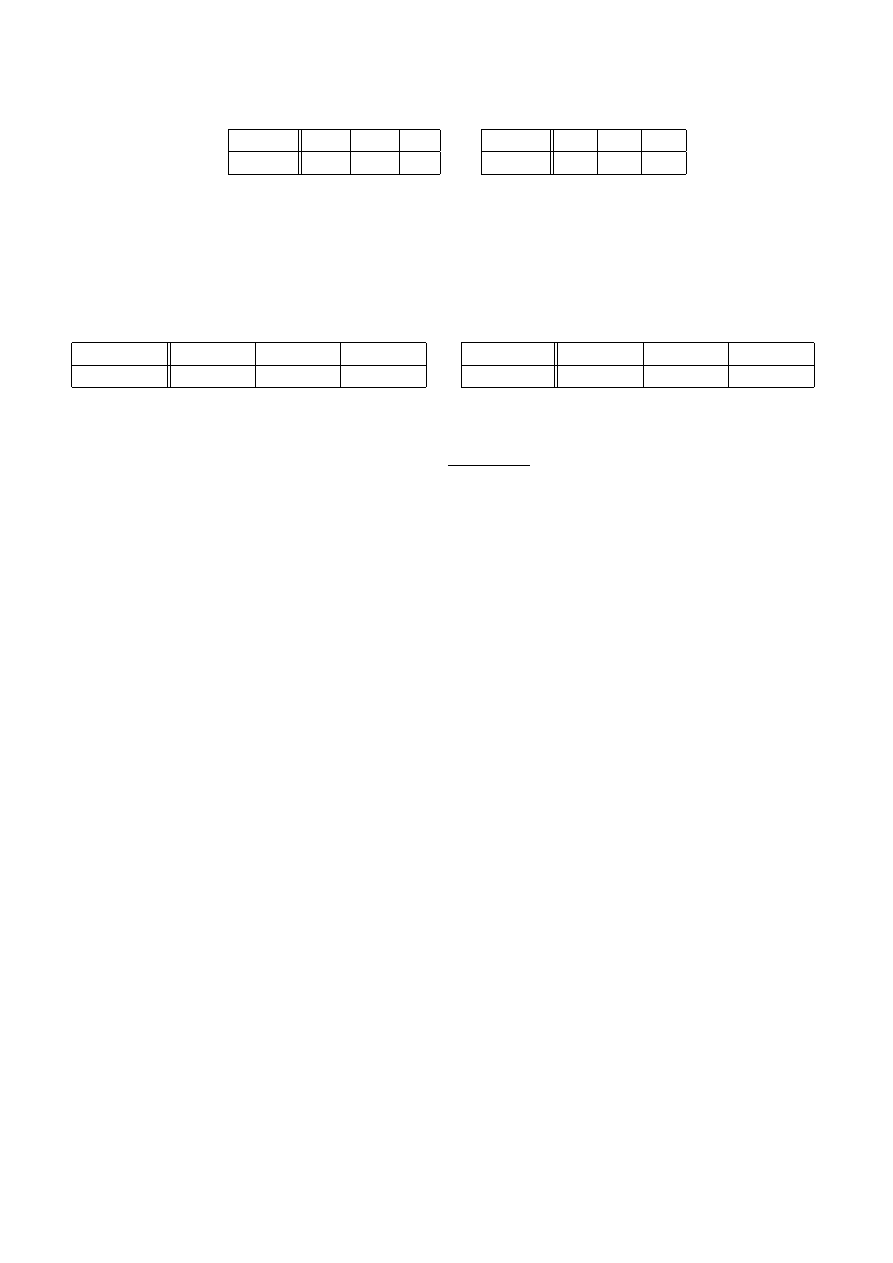
Zad. 1. Dwa dyskretne źródła wiadomości opisane są rozkładami prawdopodobieństwa podanymi w

tabelce. Obliczyć ilość informacji zawartej w każdej z wiadomości oraz dywergencję Kullbacka-Leiblera
D

KL

(P

X

, P

V

).

x

i

a

b

c

P

X

(x

i

)

0.01

0.09

0.9

x

i

a

b

c

P

V

(x

i

)

1/3

1/3

1/3

Rozwiązanie 1:

Ilość informacji zawartą w wiadomości x

i

wyznaczamy wg wzoru:

I(X = x

i

) = − log

2

(P (X = x

i

)) = − ln P (X = x

i

)/ ln 2

W naszym przypadku otrzymujemy (w przybliżeniu)

x

i

a

b

c

I(X = x

i

)

6.64 [bit]

3.47 [bit]

0.15 [bit]

x

i

a

b

c

I(V = x

i

)

1.58 [bit]

1.58 [bit]

1.58 [bit]

Z kolei dywergencja Kulbacka-Leiblera zdefiniowana jest wzorem

D

KL

(P

X

, P

V

) =

X

∀i

P (X = x

i

)· log

2

P (X = x

i

)

P (V = x

i

)

=

X

∀i

P (X = x

i

)· {log

2

P (X = x

i

) − log

2

P (V = x

i

)}

=

X

∀i

P (X = x

i

)·(I(V = x

i

) − I(X = x

i

))

W naszym przypadku :

D

KL

(P

X

, P

V

) ≈ 0.01·(1.58 − 6.64) + 0.09·(1.58 − 3.47) + 0.9·(1.58 − 0.15) ≈ 1.07

Zauważmy, że zgodnie z właściwościami dywergencji Kulbacka-Leiblera wynik jest ­ 0.

Rozwiązanie 2:

Ilość informacji zawartą w wiadomości x

i

wyznaczamy jak w pierwszym rozwiązaniu. Z

kolei dywergencję Kulbacka-Leiblera można obliczyć inaczej, korzystając z faktu, że rozkład
prawdopodobieństw opisujący źródło V jest rozkładem równomiernym. W takim przypadku
można skorzystać ze wzoru, który był wyprowadzony na ćwiczeniach.

D

KL

(P

X

, P

V

) = H

MAX

− H(X)

gdzie entropia maksymalna dla źródła X równa entropii źródła V ,

H

MAX

= log

2

M = log

2

3 ≈ 1.58 [bit]

a entropia źródła X

H(X) =

3

X

i=1

P (X = x

i

)I(X = x

i

) ≈ 0.01·6.64 + 0.09·3.47 + 0.9·0.15 [bit] ≈ 0.51 [bit]

Stąd

D

KL

(P

X

, P

V

) ≈ 1.58 − 0.51 = 1.07

Zad. 2.

Stacjonarne

źródło

binarne

generuje

wiadomości

A=„alarm”

i

B=„brak

alarmu”.

Prawdopodobieństwo pojawienia się wiadomości o alarmie wynosi P (X=A)=1/5. Prawdopodobieństwo,
utrzymania

się

stanu

alarmowego

(ponownego

nadania

wiadomości

A)

wynosi

24/25,

a

prawdopodobieństwo pojawienia się sytuacji alarmowej (nadania wiadomości A jeżeli poprzednio
była nadana wiadomość B) wynosi 1/100. Obliczyć entropię graniczną na symbol oraz entropię łączną
ciągu 3 kolejnych symboli tego źródła.

Rozwiązanie:

Ponieważ źródło jest stacjonarne możemy zapisać w ogólności:

P (X

k

= A) = P (X = A) = 1/5

oraz

P (X

k

= B) = 1 − P (X

k

= A) = 4/5

Ponadto na podstawie z treści zadania możemy określić prawdopodobieństwa warunkowe:
przejść ze stanu alarmowego (nadawanie wiadomości A) albo stanu braku alarmu (nadawanie
wiadomości B) do innego stanu lub pozostania w tym samym stanie. Zauważymy, że
prawdopodobieństwo tego, że w k + 1 chwili wiadomość przyjmie określoną postać zależy od
tego jaką postać przyjęła poprzednia wiadomość, a nie zależy od wcześniejszych wiadomości.
Źródło to zatem można opisać łańcuchem Markowa pierwszego rzędu z następującymi
prawdopodobieństwami warunkowymi:

P (X

k+1

= A|X

k

= A) = 24/25,

P (X

k+1

= B|X

k

= A) =

1/25

P (X

k+1

= A|X

k

= B) = 1/100,

P (X

k+1

= B|X

k

= B) = 99/100

W przypadku stacjonarnego źródła dającego się opisać łańcuchem Markowa pierwszego rzędu
entropia graniczna na symbol H

∞

jest równa średniej entropii warunkowej bieżącego symbolu X

2

pod warunkiem, że znany jest symbol poprzedni X

1

.

H

∞

(X) = H(X

2

|X

1

) =

X

∀i

P (X

1

= x

i

)·H(X

2

|X

1

= x

i

)

gdzie entropia warunkowa symbolu X

2

pod warunkiem, że poprzedni symbol X

1

przyjął postać x

i

jest wyrażona wzorem:

H(X

2

|X

1

= x

i

) = −

X

∀j

P (X

2

= x

j

|X

1

= x

i

) log

2

(P (X

2

= x

j

|X

1

= x

i

))

W naszym przypadku:

H(X

2

|X

1

= A)

=

−P (X

2

= A|X

1

= A) log

2

(P (X

2

= A|X

1

= A)) +

−P (X

2

= B|X

1

= A) log

2

(P (X

2

= B|X

1

= A))

=

−

24

25

log

2

24

25

−

1

25

log

2

1

25

≈ 0.24 [bit]

oraz

H(X

2

|X

1

= B)

=

−P (X

2

= A|X

1

= B) log

2

(P (X

2

= A|X

1

= B)) +

−P (X

2

= B|X

1

= B) log

2

(P (X

2

= B|X

1

= B))

=

−

1

100

log

2

1

100

−

99

100

log

2

99

100

≈ 0.08 [bit]

stąd średnia entropia warunkowa

H(X

2

|X

1

)

=

P (X

1

= A)H(X

2

|X

1

= A) + P (X

1

= B)H(X

2

|X

1

= B)

≈

1

5

0.24 +

4

5

0.08 ≈ 0.11 [bit]

Czyli graniczna entropia na symbol rozpatrywanego źródła H

∞

(X) ≈ 0.11 [bit].

Pozostaje jeszcze wyznaczyć entropię łączną ciągu trzech kolejnych symboli. Można
wyznaczyć ją ze wzoru

H(X

1

, X

2

, . . . , X

N

) = H(X

1

) + H(X

2

|X

1

) + . . . + H(X

N

|X

1

, X

2

, . . . , X

N −1

)

który w przypadku stacjonarnego źródła opisanego łańcuchem Markowa pierwszego rzędu
(dla którego H(X

N

|X

1

, X

2

, . . . , X

N −1

) = H(X

2

|X

1

)) można sprowadzić do postaci:

H(X

1

, X

2

, . . . , X

N

) = H(X

1

) + (N − 1)·H(X

2

|X

1

)

(1)

Średnia entropia warunkowa H(X

2

|X

1

) jest już obliczona, musimy zatem jeszcze obliczyć

entropię źródła H(X

1

) = H(X)

H(X

1

) = H(X) = −P (X = A)· log

2

P (X = A) − P (X = B)· log

2

P (X = B)

=

1

5

log

2

5 +

4

5

log

2

5

4

≈

1

5

2.32 +

4

5

0.32

= 0.72 [bit]

Podsumowując na podstawie wzoru (1) entropia łączna ciągu trzech kolejnych wiadomości
wynosi

H(X

1

, X

2

, X

3

) = H(X) + 2·H(X

2

|X

1

) ≈ 0.72 + 2·0.11 = 0.94 [bit/symbol]