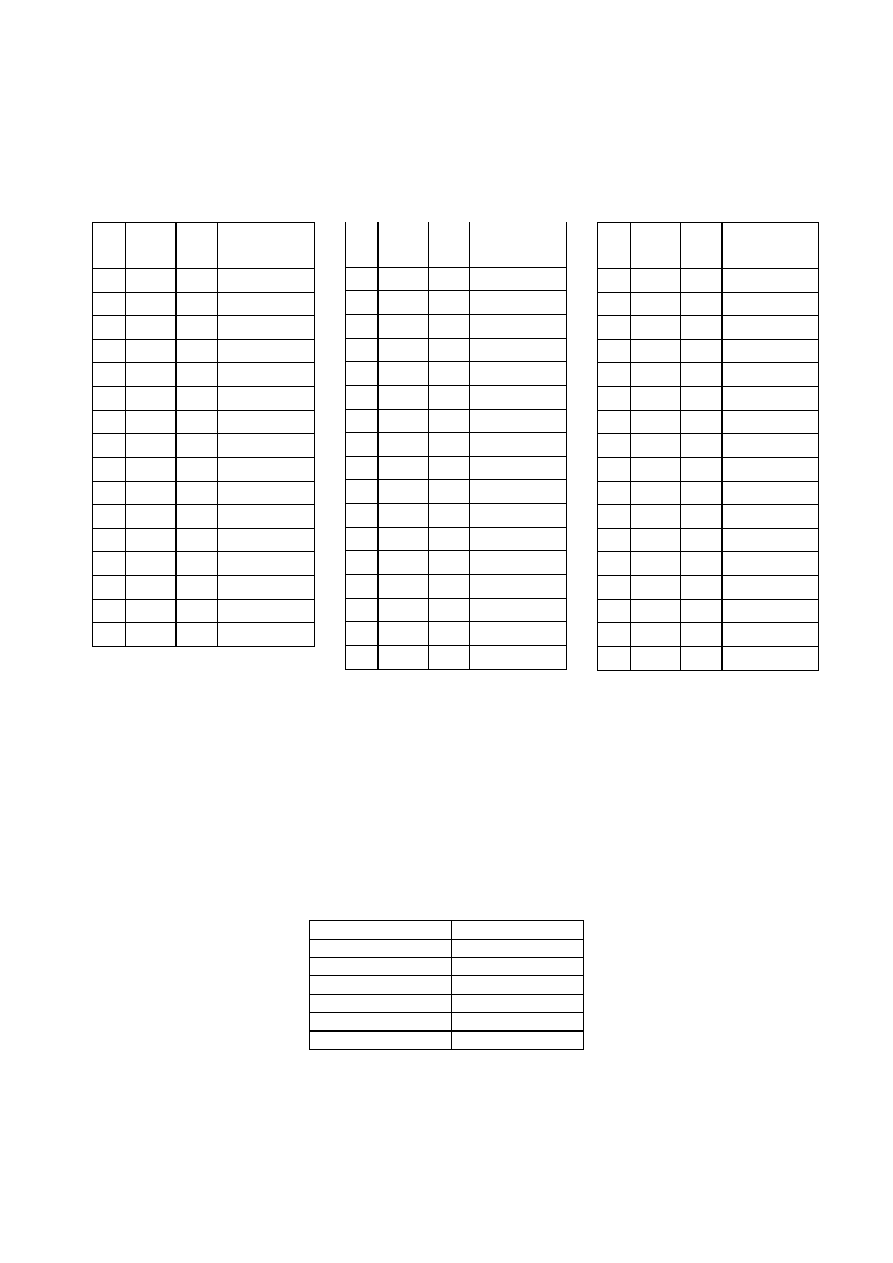
Laboratorium 1, 2
METODY OPISU STATYSTYCZNEGO
ZAD. 1
Dane o wadze (w dkg), płci oraz kolejności urodzenia przez matkę dla 50 noworodków wybranych losowo na
podstawie dokumentacji pewnego szpitala są następujące:
Lp waga płeć
kolejność
urodzenia
1
366
z
6
2
368
m
2
3
365
z
1
4
395
m
2
5
377
z
4
6
353
m
6
7
318
z
1
8
307
z
4
9
403
z
2
10
433
m
4
11
235
z
2
12
520
m
2
13
341
z
1
14
358
z
2
15
365
m
1
16
350
m
1
Lp waga płeć
kolejność
urodzenia
17
419
z
2
18
370
z
2
19
378
z
2
20
336
z
3
21
310
z
2
22
363
m
1
23
190
z
1
24
349
m
4
25
353
m
2
26
319
m
4
27
332
z
1
28
262
m
4
29
323
m
4
30
460
m
2
31
310
z
4
32
321
m
3
33
265
z
1
Lp waga płeć
kolejność
urodzenia
34
391
m
1
35
385
z
2
36
244
z
1
37
447
m
3
38
437
z
1
39
385
z
2
40
299
z
3
41
352
z
5
42
425
m
3
43
415
z
2
44
240
m
1
45
434
m
3
46
329
z
2
47
375
m
1
48
309
z
5
49
403
m
5
50
255
m
1
1.
Zapisać dane w zbiorze o nazwie OPIS tworząc wektory waga, plec, kolejn.
2.
Utwórz nową zmienną waga_kg zawierającą wagę w kg.
3.
Wyznaczyć szeregi rozdzielcze:
a)
waga (typ ciągły, 10 klas, rozpocząć od 170, szerokość przedziałów 36);
b)
kolejn (typ skokowy, 6 klas).
4.
Wyznaczyć podstawowe parametry opisowe dla zmiennej waga.
5.
Wyznaczyć 34-ty percentyl, 2-gi decyl dla zmiennej waga.
6.
Obliczyć względne częstości skumulowane rozkładu zmiennej waga_kg dla klas o rozpiętości 0,5 kg,
rozpoczynając od 1,5 pierwszy przedział klasowy.
ZAD. 2
Rozkład czasu rozwiązywania pewnego testu w grupie 50 uczniów był następujący:
Czas w minutach
Liczba uczniów
3 - 5
9
5 - 7
17
7 - 9
13
9 - 11
6
11 - 13
3
13 - 15
2
Obliczyć i zinterpretować średnią, odchylenie standardowe oraz współczynnik zmienności czasu
rozwiązywania pewnego testu przez uczniów.
ZAD. 3
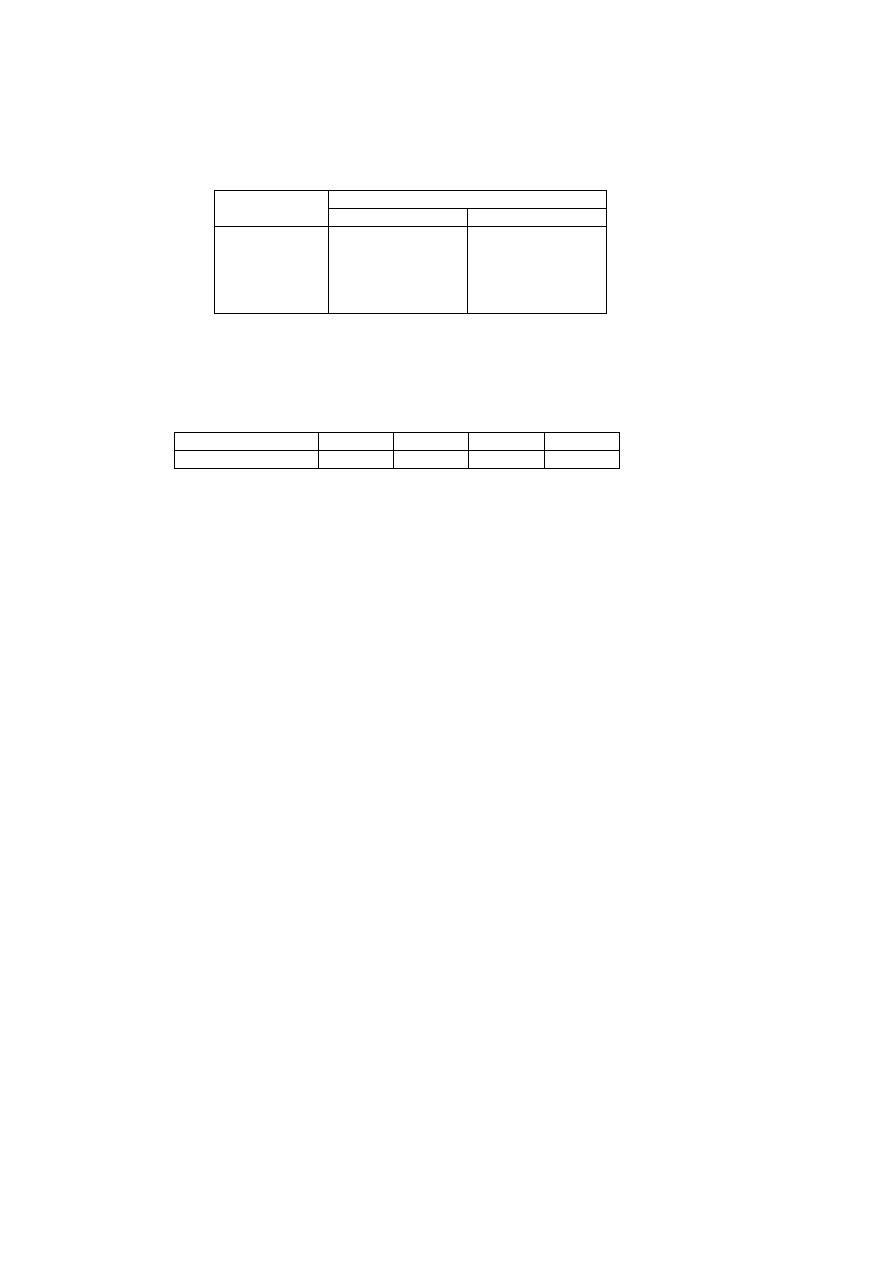
W sondażu przeprowadzonym wśród 60 losowo wybranych klientów firmy zajmującej się dystrybucją
kawy na temat ocen jakości dwóch gatunków kawy Pedro’s, a mianowicie Pedro’s Gastronet i Pedro’s Feinster,
uzyskano dane zawarte w następującej tablicy:
Liczba klientów
Ocena w
punktach
Kawa Gastronet
Kawa Feinster
3
4
5
6
7
4
14
17
19
6
6
16
21
13
4
1.
Który z gatunków kawy cieszy się lepszą opinią wśród zbadanych klientów? Odpowiedź uzasadnić,
wykorzystując znane miary średniego poziomu.
2.
Porównać dyspersję i spłaszczenie obu rozkładów.
ZAD. 4
W wyniku badania liczby dzieci urodzonych w Tarnowie w 2003 r. przez 500 losowo wybranych kobiet
w wieku 20-24 lat otrzymano następujący rozkład:
Liczba dzieci
0
1
2
3
Liczba kobiet
75
365
45
15
Ocenić dyspersję i asymetrię rozkładu.
ZAD. 5
Obserwacje prowadzone przez służbę leśną dostarczyły wyników pomiarów średnic (w cm) dębów na wysokości
1 m:
8,5
2,3
9,5
4,8
7,2
9,8
3,0
6,7
6,1
5,8
4,5 10,8
4,1
4,5
8,8 10,3
11,4
8,2
9,1
7,7
9,6
8,2
5,1
9,4
9,4
7,9
6,2
5,0
7,2
9,4
6,9
5,5
7,6
9,6 12,8
6,5
3,8
6,9 10,7
8,0
5,1
6,8
7,7
9,3
6,3
7,0
7,2
7,3
6,3
7,3 11,0
8,7
5,0
5,3
5,7
4,4
11,6
9,3
8,3
6,9
7,0
6,1
6,4
7,8
4,0
7,4
4,9
2,7
8,5 15,2
7,5
8,9
8,1
5,9
7,5
8,6
9,7
5,6
5,7
2,5
1.
Wyznaczyć średnią, odchylenie standardowe, medianę, modę, kwartyle, współczynnik zmienności,
współczynnik skośności, kurtozę i podać ich interpretację.
2.
Pogrupuj pomiary średnic dębów z laboratorium 1 w szereg rozdzielczy o szerokości klas 2 cm
poczynając od dolnej granicy pierwszej klasy 2 cm. Wyznaczyć średnią i nieobciążoną wariancję na
podstawie szeregu i na podstawie wyjściowych danych. Wyjaśnij różnicę między nimi.
ZAD. 6
Na podstawie analizy 50 ofert turystycznych, w których proponowano w maju 1994 roku wczasy w
basenie Morza śródziemnego, uzyskano następujące dane dotyczące długości oferowanego wypoczynku w
dniach:
8
18
13
15
17
14
12
16
12
12
9
17
14
13
13
11
9
10
15
16
10
16
14
14
13
11
10
13
13
12
15
13
11
13
12
12
12
14
11
14
16
12
13
13
14
12
13
12
15
13
1.
Zbudować punktowy szereg rozdzielczy ofert ze względu na długość proponowanego wypoczynku.
2.
Ocenić przeciętny czas oferowanych wczasów oraz zróżnicowanie za pomocą odchylenia standardowego
i współczynnika zmienności.