Strona 1 z 9
ZADANIE II
Rozwi
ą
za
ć
belk
ę
ci
ą
gł
ą
statycznie niewyznaczaln
ą
metod
ą
trzech momentów.
Sporz
ą
dzi
ć
wykresy sił przekrojowych M i T.
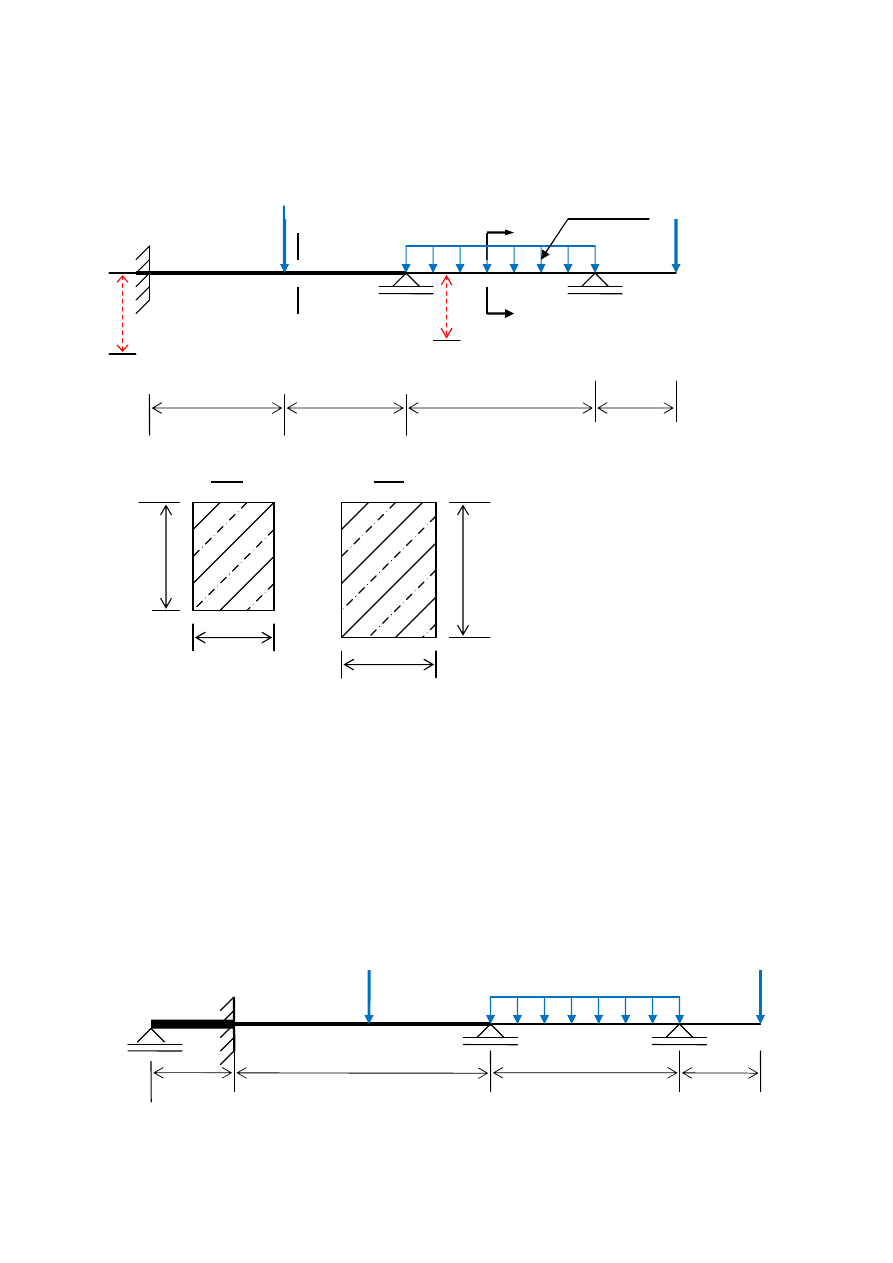
Rys. 1
1. Obliczenia pomocnicze
Przyjmujemy schemat pomocniczy (rys.2), w którym w zwi
ą
zku z tym,
ż
e podpor
ą
nieprzesuwn
ą
jest
utwierdzenie ko
ń
ca belki, wprowadzamy dodatkowe fikcyjne prz
ę
sło o
0
=
l
i
0
=
EJ
.
Numerujemy w
ę
zły belki (zaczynaj
ą
c od zera - bowiem jest najwygodniej).
Wprowadzamy numeracj
ę
prz
ę
seł – numer prz
ę
sła jest równy numerowi w
ę
zła opisuj
ą
cego koniec
prz
ę
sła (licz
ą
c od lewej do prawej). Znaj
ą
c nr prz
ę
sła opisa
ć
mo
ż
emy w danym prz
ęś
le jego długo
ść
i
sztywno
ść
.
Rys. 2.
1
2
3
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
l
2
=12 [m]
EJ
2
l
3
=8 [m]
EJ
3
l
4
=3 [m]=a
EJ
4
4
l
1
=0
EJ
1
=∞
0
A-A
B-B
b
1
=0,3[m]
b
1
=0,3[m]
h
1
=
0
,4
[m
]
h
2
=
0
,4
[m
]
∆
y1
=6 mm
1
2
3
t
g
=0
0
C
t
d
=10
0
C
t
g
=0
0
C
t
d
=15
0
C
∆
y2
=10 mm
A
A
B
B
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
6 m
6 m
8 m
3 m
[
]
[ ]
C
/
m
/
kN
E
o
t
1
10
1
10
2
5
2
7
−
⋅
=
⋅
=
α
Strona
2 z 9
Stopie
ń
statycznej niewyznaczalno
ś
ci tej belki wynosi: SSN=2
Z rys. nr 1 wynika,
ż
e sztywno
ś
ci we wszystkich prz
ę
słach s
ą
ró
ż
ne (ale w danym prz
ęś
le takie same –
co wynika z def. belki ci
ą
głej).
Obliczamy momenty bezwładno
ś
ci w poszczególnych prz
ę
słach, bowiem od nich zale
żą
sztywno
ś
ci w
tych prz
ę
słach.
W prz
ęś
le 1-2 mamy:
[ ]
4
2
3
3
2
10
3125
,
0
12
5
,
0
3
,
0
12
m
bh
J
−
⋅
=
⋅
=
=
,
W prz
ęś
le 2-3 oraz 3-4 mamy:
[ ]
4
4
2
3
3
3
10
54
,
0
12
6
,
0
3
,
0
12
J
m
bh
J
=
⋅
=
⋅
=
=
−
,
Teraz przyjmujemy jako porównawczy moment bezwładno
ś
ci - moment w bezwładno
ś
ci w prz
ęś
le 1-2,
czyli
0
2
J
J
=
i w poszczególnych prz
ę
słach opisujemy sztywno
ś
ci tzw. sztywno
ś
ci
ą
porównawcz
ą
0
EJ
. (
E
jest stałe dla wszystkich prz
ę
seł, natomiast zmienny jest moment bezwładno
ś
ci).
Za sztywno
ść
porównawcz
ą
przyjmujemy np. sztywno
ść
prz
ę
sła 1-2, czyli:
[ ]
0
4
2
2
10
3125
,
0
EJ
m
E
EJ
=
⋅
⋅
=
−
.
Wyra
ż
amy pozostałe sztywno
ś
ci uzale
ż
niaj
ą
c je od sztywno
ś
ci
0
EJ
:
2
2
2
0
0
3
3
10
3125
,
0
10
3125
,
0
10
54
,
0
−
−
−
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
=
E
E
E
EJ
EJ
EJ
EJ
[ ]
4
4
0
3
728
,
1
EJ
m
EJ
EJ
=
⋅
=
Wyliczenie długo
ś
ci sprowadzonych prz
ę
seł:
Wzór ogólny:
k
k
k
l
EJ
EJ
l
⋅
=
0
'
:
]
[
12
12
0
0
2
2
0
'
2
m
EJ
EJ
l
EJ
EJ
l
=
⋅
=
⋅
=
,
]
[
63
,
4
8
728
,
1
0
0
3
3
0
'
3
m
EJ
EJ
l
EJ
EJ
l
≅
⋅
⋅
=
⋅
=
,
'
0
0
4
4
0
'
4
]
[
74
,
1
3
728
,
1
a
m
EJ
EJ
l
EJ
EJ
l
=
≅
⋅
⋅
=
⋅
=
.
2. Przyj
ę
cie schematu podstawowego
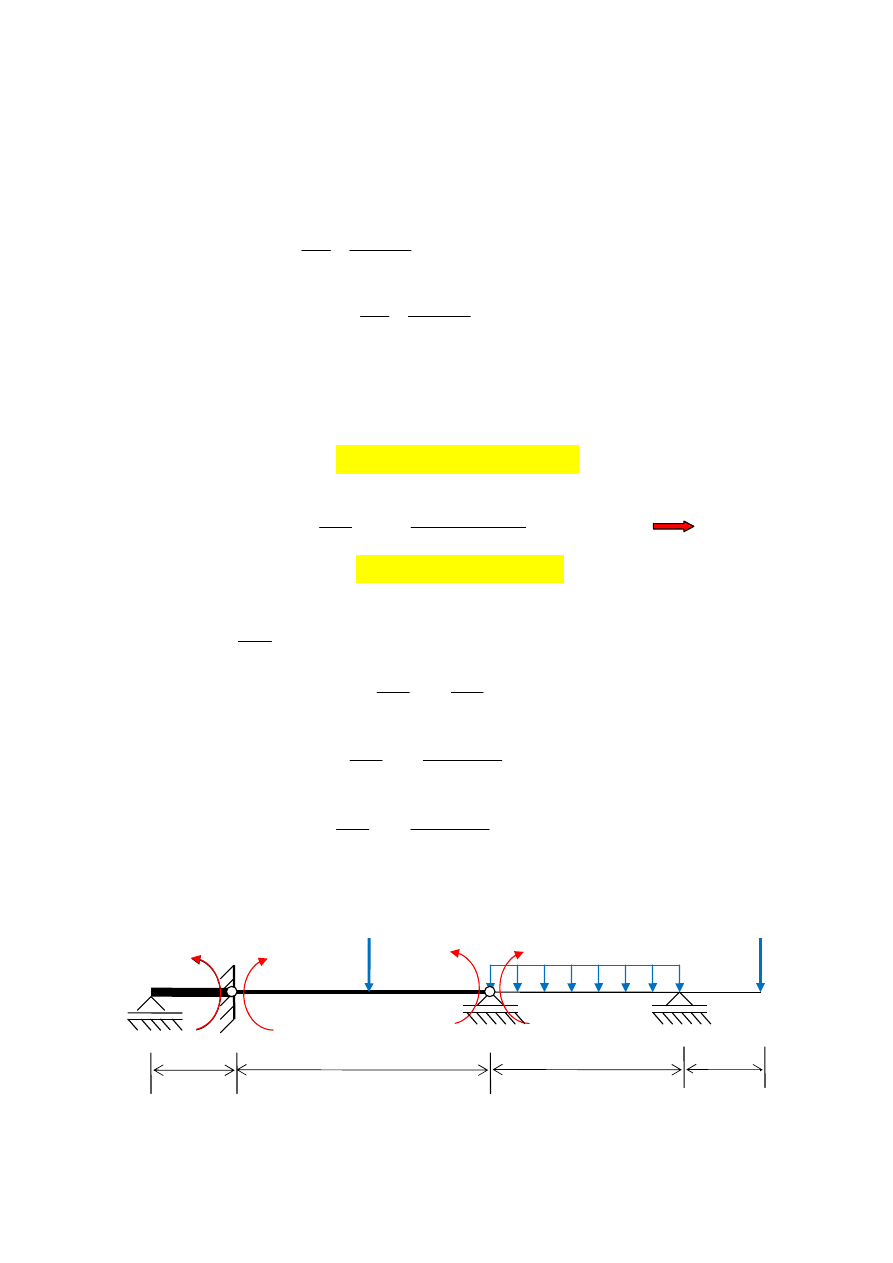
Rys. 3
1
2
3
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
l
2
=12 [m]
EJ
2
l
3
=8 [m]
EJ
3
l
4
=3 [m]=a
EJ
4
4
l
1
=0
EJ
1
=∞
0
l
1
’
=0
l
2
’
=12, EJ
0
l
3
’
=12, 1,728·EJ
0
l
4
’
=12
1,728·EJ
0
X
1
X
1
X
2
X
2
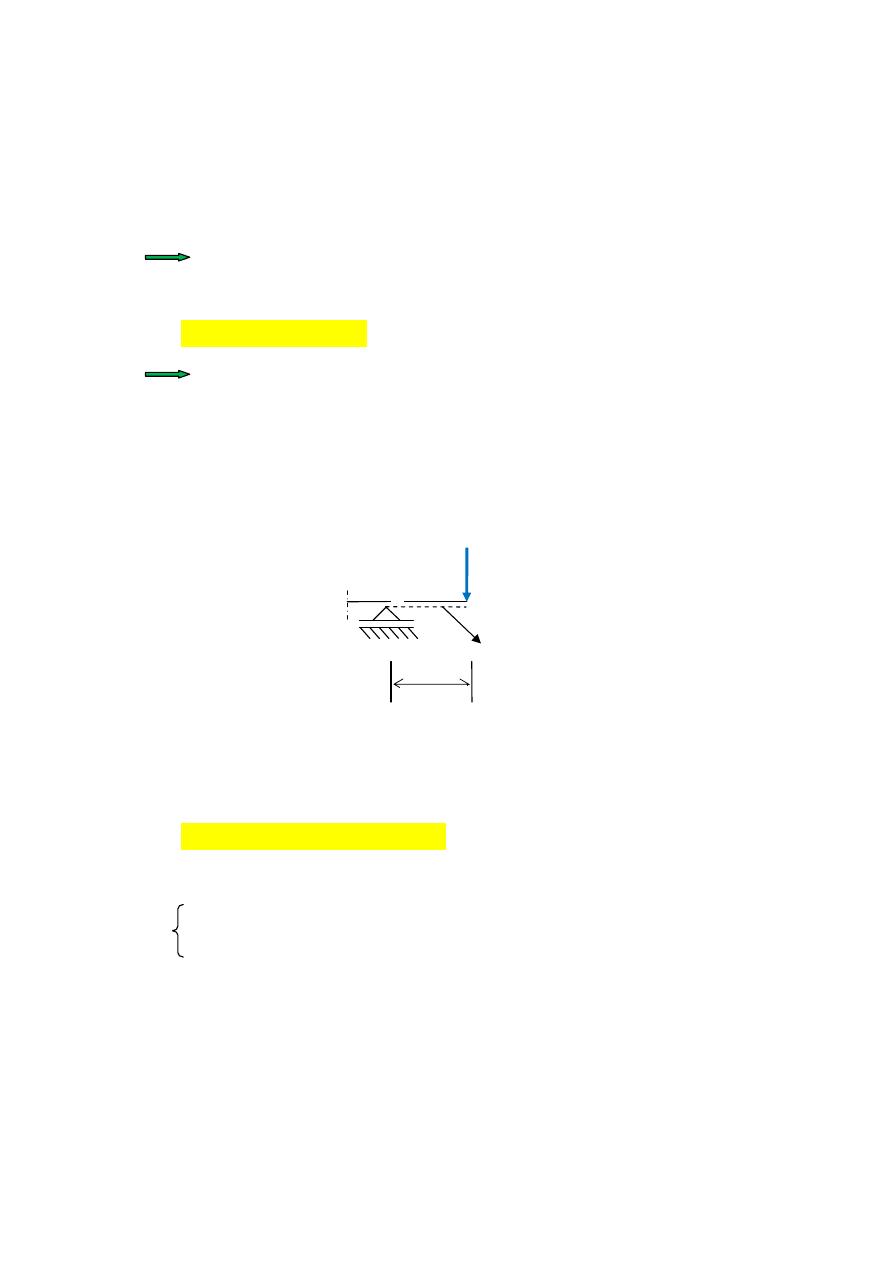
Strona
3 z 9
3. Równania trzech momentów
Układamy równania (ci
ą
gło
ś
ci) kolejno w podporach, w których wprowadzono nadliczbowe
k
X
(w miejsce
zwolnionych wi
ę
zów).
Ogólny wzór metody trzech momentów zapisany w w
ęź
le „
k
”:
0
0
1
'
1
'
1
'
1
'
6
)
(
2
k
k
k
k
k
k
k
k
EJ
X
l
X
l
l
X
l
δδδδ
−
=
+
+
+
+
+
+
−
.
k=1
10
0
2
'
2
0
'
2
'
1
0
'
1
6
)
(
2
δδδδ
EJ
X
l
X
l
l
X
l
−
=
+
+
+
,
10
0
2
0
0
6
12
)
12
0
(
2
0
δδδδ
EJ
X
X
X
−
=
⋅
+
+
+
⋅
,
10
0
2
1
6
12
24
δδδδ
EJ
X
X
−
=
+
,
k=2
20
0
3
'
3
2
'
3
'
2
1
'
2
6
)
(
2
δδδδ
EJ
X
l
X
l
l
X
l
−
=
+
+
+
,
20
0
3
2
1
6
63
,
4
)
63
,
4
12
(
2
12
δδδδ
EJ
X
X
X
−
=
+
+
+
,
W naszym zadaniu moment przypodporowy w w
ęź
le „3” (
3
X
) jest ró
ż
ny od zera i jest momentem zna-
nym (znak „-„ poniewa
ż
ś
ciska dolne włókna):
]
[
18
3
6
4
2
3
KNm
l
P
X
−
=
⋅
−
=
⋅
−
=
.
Rys. 4
20
0
2
1
6
)
18
(
63
,
4
)
63
,
4
12
(
2
12
δδδδ
EJ
X
X
−
=
−
⋅
+
+
+
,
20
0
2
1
6
34
,
83
26
,
33
12
δδδδ
EJ
X
X
−
=
+
+
,
34
,
83
6
26
,
33
12
20
0
2
1
−
−
=
+
δδδδ
EJ
X
X
Ostatecznie otrzymujemy układ 2 równa
ń
do rozwi
ą
zania:
10
0
2
1
6
12
24
δδδδ
EJ
X
X
−
=
+
34
,
83
6
26
,
33
12
20
0
2
1
−
−
=
+
δδδδ
EJ
X
X
4. Obliczenie
0
k
δδδδ
, tj.
10
δδδδ
i
20
δδδδ
Ogólny wzór na
0
k
δδδδ
ma posta
ć
:
∆
+
+
=
k
kt
kp
k
δδδδ
δδδδ
δδδδ
δδδδ
0
4.1.
Wyznaczenie
kp
δδδδ
Mo
ż
na wyliczy
ć
dwoma sposobami: metod
ą
Mohra lub z wykorzystanie równania prac wirtualnych
W naszym zadaniu wykorzystamy równanie prac wirtualnych do obliczenia
kp
δδδδ
.
3
P
2
=6 kN
l
4
=3 [m]=a
4
wyróżnione włókna
Strona
4 z 9
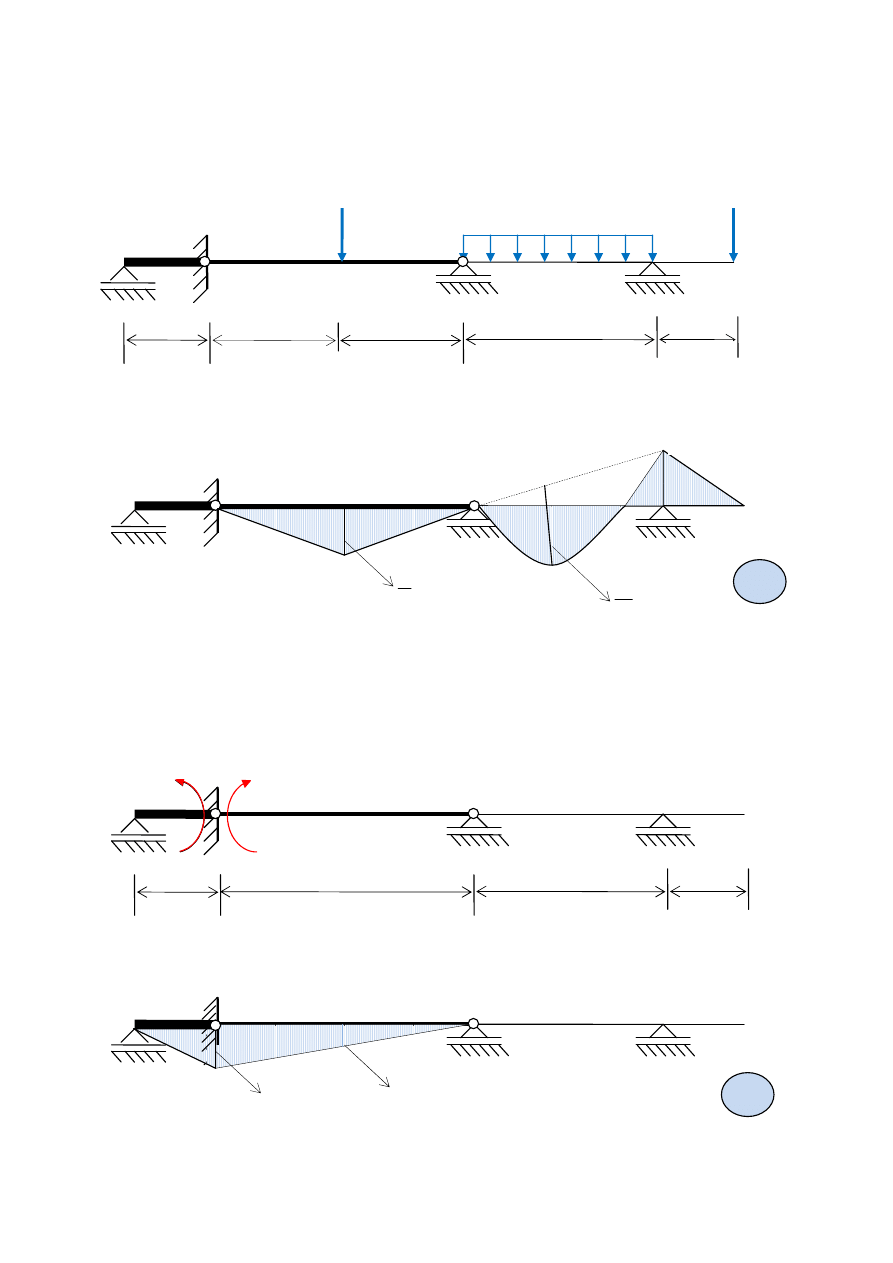
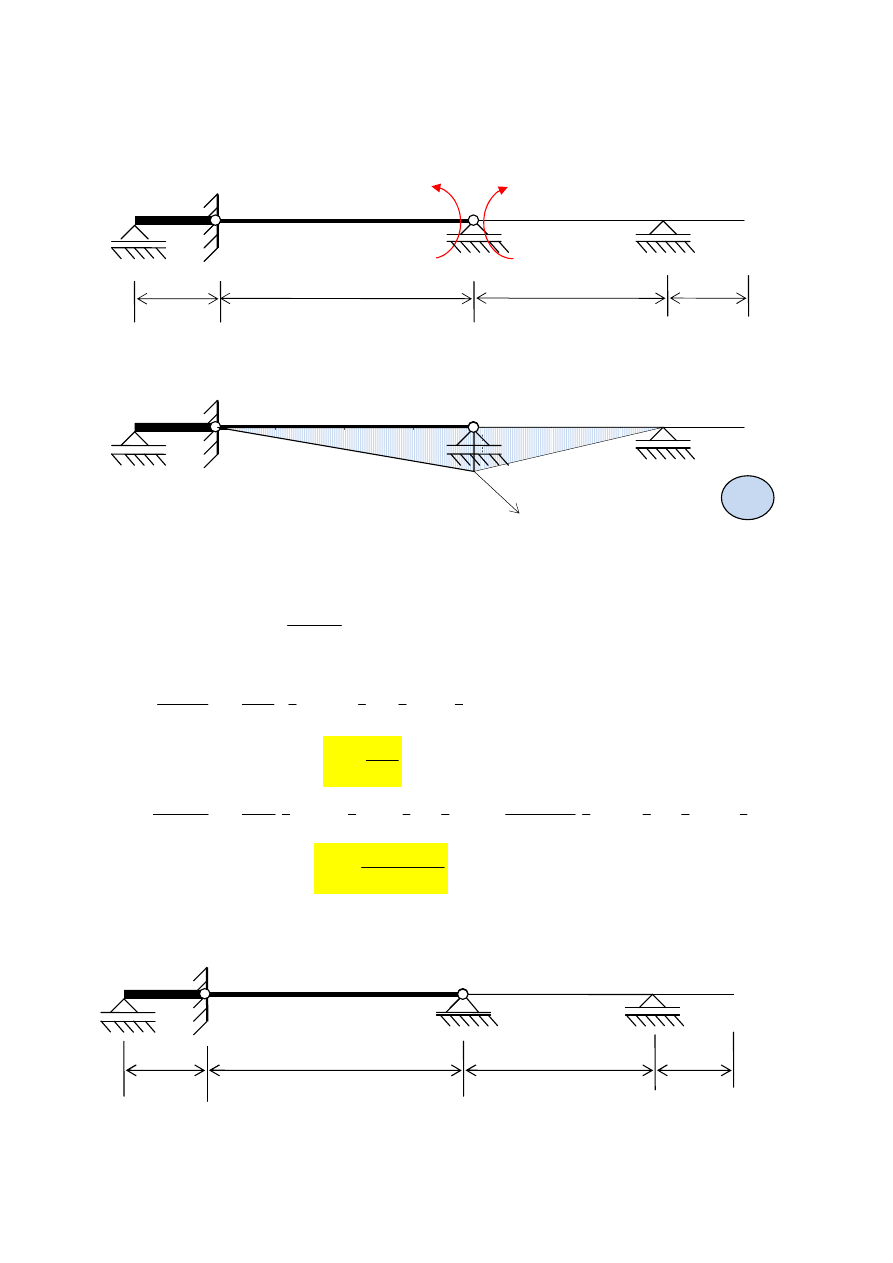
Wykres momentów zginaj
ą
cych (rys. 5b) w schemacie podstawowym od obci
ąż
enia „p” (rys. 5a):
a)
b)
Rys. 5
Wykres momentów zginaj
ą
cych (rys. 6b) w schemacie podstawowym od stanu
1
1
=
X
(rys. 6a):
a)
b)
Rys. 6
1
2
3
4
0
0,5
M
1
1
1
2
3
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 =a
4
l
1
=0
EJ
1
=∞
0
l
1
’
=0
EJ
0
1,728·EJ
0
X
1
=1
X
1
=1
1
2
3
4
0
36
4
=
Pl
48
8
2
=
ql
M
p
18
1
2
3
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
l
2
=12
l
3
=8 [m]
l
4
=3 [m]=a
4
l
1
=0
0
l
1
’
=0
EJ
0
1,728·EJ
0
6 [m]
6 [m]
Strona
5 z 9
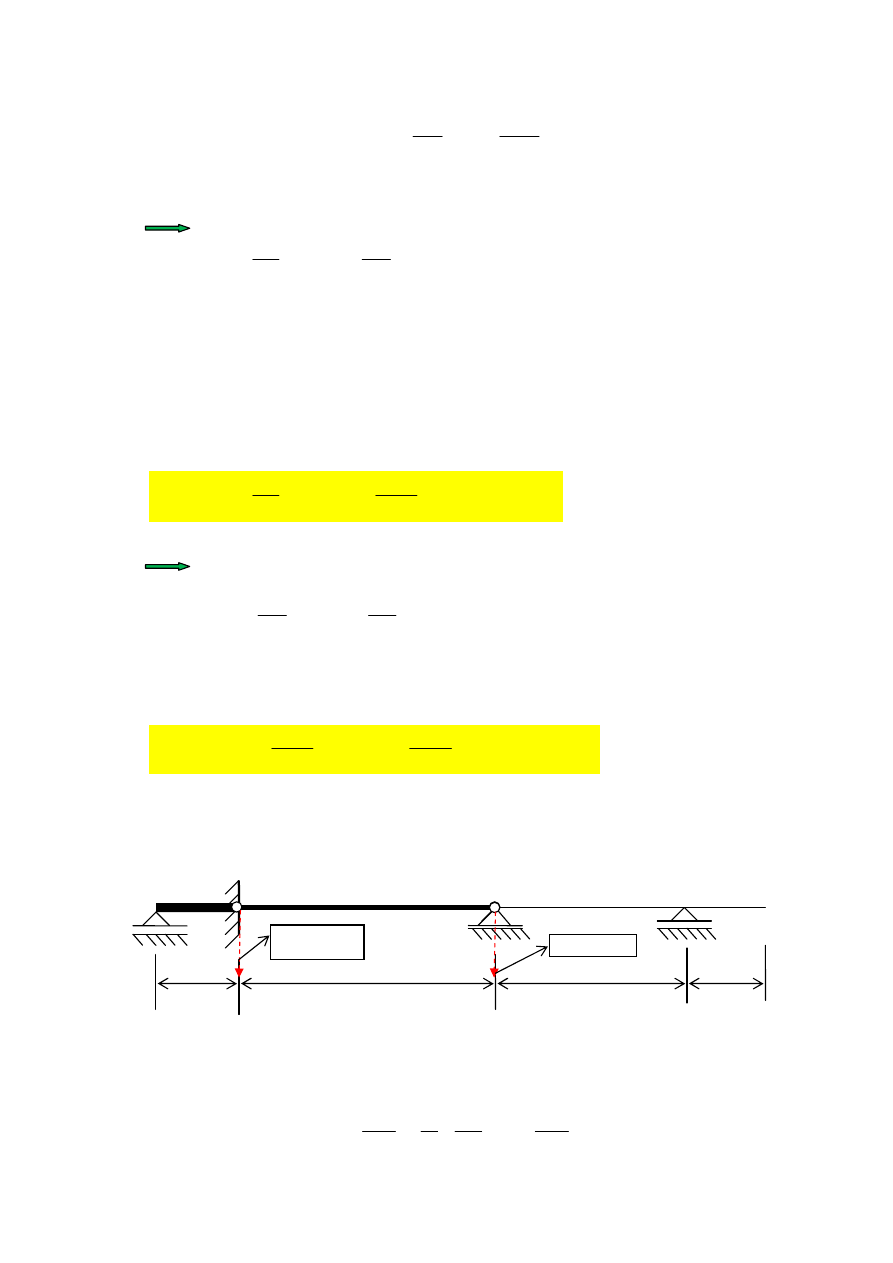
Wykres momentów zginaj
ą
cych (rys. 7b) w schemacie podstawowym od stanu
1
2
=
X
(rys. 7a):
a)
b)
Rys. 7
Współczynniki
kp
δδδδ
obliczamy wg wzoru:
0
1
108
EJ
p
=
δδδδ
(
)
[
]
[
]
=
⋅
⋅
⋅
⋅
−
⋅
⋅
⋅
⋅
+
⋅
+
⋅
+
⋅
⋅
⋅
⋅
=
=
∫
1
8
18
1
8
48
728
,
1
1
5
,
0
1
5
,
0
6
36
1
3
1
2
1
2
1
3
2
0
3
2
3
1
3
2
2
1
0
2
2
EJ
EJ
ds
EJ
M
M
l
p
p
δδδδ
0
2
185185
,
168
EJ
p
≅
δδδδ
4.2.
Wyznaczenie
kt
δδδδ
:
Rys. 8
1
2
3
4
0
10
o
C
0
o
C
0
o
C
15
o
C
0
o
C
15
o
C
l
1
=0
l
2
=12
l
3
=8
l
4
=3
1
2
3
4
0
M
2
1
1
2
3
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 =a
4
l
1
=0
EJ
1
=∞
0
l
1
’
=0
EJ
0
1,728·EJ
0
X
2
=1
X
2
=1
ds
EJ
M
M
l
p
k
kp
∫
=
δδδδ
[
]
=
⋅
+
⋅
+
⋅
⋅
⋅
⋅
⋅
=
=
∫
)
5
,
0
5
,
0
1
(
6
36
1
3
2
3
2
3
1
2
1
0
1
1
EJ
ds
EJ
M
M
l
p
p
δδδδ
Strona
6 z 9
Ogólny wzór na wyznaczenie
kt
δδδδ
:
1
1
1
2
2
1
+
+
+
∆
⋅
⋅
+
⋅
∆
⋅
=
+
k
k
k
t
k
k
k
t
kt
t
h
l
h
l
t
k
k
αααα
αααα
δδδδ
,
gdzie
g
d
t
t
t
−
=
∆
.
Wyliczamy kolejno w w
ę
złach, w których wprowadzono nadliczbowe
k
X
:
k=1
2
2
2
1
1
1
1
2
2
2
1
h
l
t
h
l
t
t
t
t
⋅
∆
⋅
+
⋅
∆
⋅
=
αααα
αααα
δδδδ
,
C
t
0
1
0
=
∆
,
C
C
C
t
0
0
0
2
10
0
10
=
−
=
∆
,
∞
→
1
h
,
m
5
,
0
2
=
h
,
m
0
1
=
l
,
m
12
2
=
l
,
C
const
t
0
1/
5
10
1
−
⋅
=
=
αααα
,
3
5
1
1
1
10
2
,
1
0012
,
0
5
,
0
2
12
10
10
1
2
0
1
−
−
⋅
=
=
⋅
⋅
⋅
⋅
+
⋅
∆
⋅
=
h
t
t
t
αααα
δδδδ
k=2
3
3
3
2
2
2
2
2
2
3
2
h
l
t
h
l
t
t
t
t
⋅
∆
⋅
+
⋅
∆
⋅
=
αααα
αααα
δδδδ
,
C
C
C
t
0
0
0
3
15
0
15
=
−
=
∆
,
m
6
,
0
3
=
h
,
m
8
3
=
l
,
3
5
5
2
10
2
,
2
0022
,
0
6
,
0
2
8
15
10
1
5
,
0
2
12
10
10
1
−
−
−
⋅
=
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
=
t
δδδδ
.
4.3.
Wyznaczenie
∆
k
δδδδ
:
Rys. 9
Ogólny wzór na wyznaczenie
∆
k
δδδδ
:
1
1
1
1
1
1
+
+
+
−
∆
∆
+
∆
⋅
+
−
∆
=
k
k
i
k
k
k
k
k
l
l
l
l
δδδδ
.
1
2
3
4
0
l
1
=0
l
2
=12
l
3
=8
l
4
=3
∆
y1
=0,006 m
∆
y2
=0,01 m
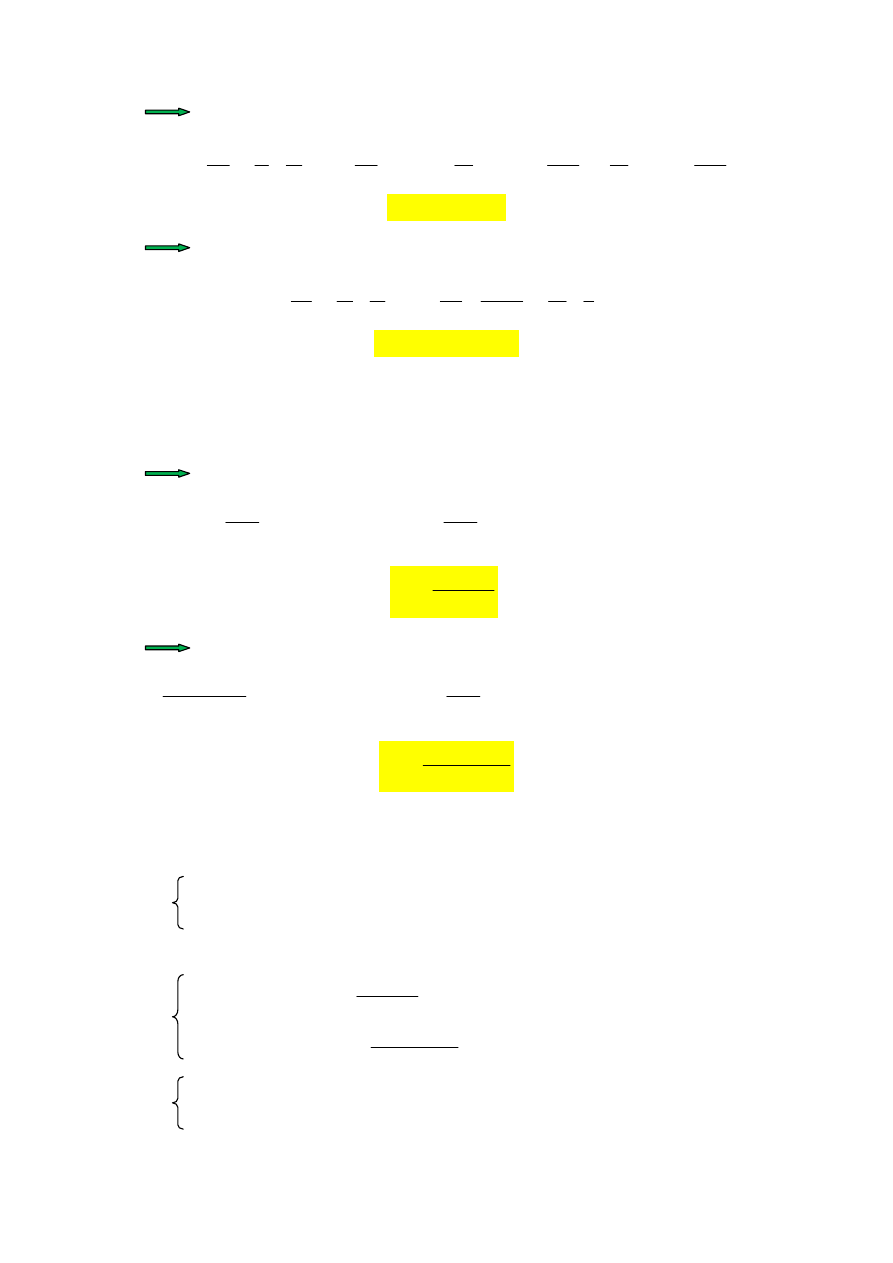
Strona
7 z 9
k=1
12
01
,
0
006
,
0
12
1
12
01
,
0
006
,
0
12
1
0
0
1
1
2
2
1
2
1
1
0
1
+
⋅
−
=
+
⋅
+
−
=
∆
+
∆
⋅
+
−
∆
=
∆
l
l
l
l
δδδδ
4
1
10
)
3
(
,
3
−
∆
⋅
=
δδδδ
k=2
0
01
,
0
8
1
12
1
12
006
,
0
1
1
3
3
2
3
2
2
1
2
+
⋅
+
−
=
∆
+
∆
⋅
+
−
∆
=
∆
l
l
l
l
δδδδ
3
2
10
)
3
(
58
,
1
−
∆
⋅
−
=
δδδδ
4.4.
Wyznaczenie
0
k
δδδδ
:
∆
+
+
=
k
kt
kp
k
δδδδ
δδδδ
δδδδ
δδδδ
0
.
k=1
[
]
4
3
0
0
4
3
0
10
10
)
3
(
,
3
10
2
,
1
(
108
1
10
)
3
(
,
3
10
2
,
1
108
−
−
−
−
⋅
+
⋅
⋅
+
=
⋅
+
⋅
+
=
EJ
EJ
EJ
δδδδ
,
0
10
)
3
(
8
,
203
EJ
=
δδδδ
,
k=2
[
]
3
3
0
0
3
3
0
20
10
)
3
(
58
,
1
10
2
,
2
(
18518
,
258
1
10
)
3
(
58
,
1
10
2
,
2
185185
,
168
−
−
−
−
⋅
−
⋅
⋅
+
=
⋅
−
⋅
+
=
EJ
EJ
EJ
δδδδ
0
20
726852
,
206
EJ
=
δδδδ
5. Rozwi
ą
zanie układu równa
ń
- wyliczenie
k
X
Wracamy do układu równa
ń
10
0
2
1
6
12
24
δδδδ
EJ
X
X
−
=
+
34
,
83
6
26
,
33
12
20
0
2
1
−
−
=
+
δδδδ
EJ
X
X
Za
0
k
δδδδ
wstawiamy wyliczone wielko
ś
ci w pkt. 4.:
0
0
2
1
)
3
(
8
,
203
6
12
24
EJ
EJ
X
X
⋅
−
=
+
34
,
83
726852
,
206
6
26
,
33
12
0
0
2
1
−
−
=
+
EJ
EJ
X
X
0
2
1
1223
12
24
EJ
X
X
−
=
+
0
2
1
7
,
1323
26
,
33
12
EJ
X
X
−
=
+
Strona
8 z 9
8952
,
37
1
−
≅
X
1262
,
26
1
−
≅
X
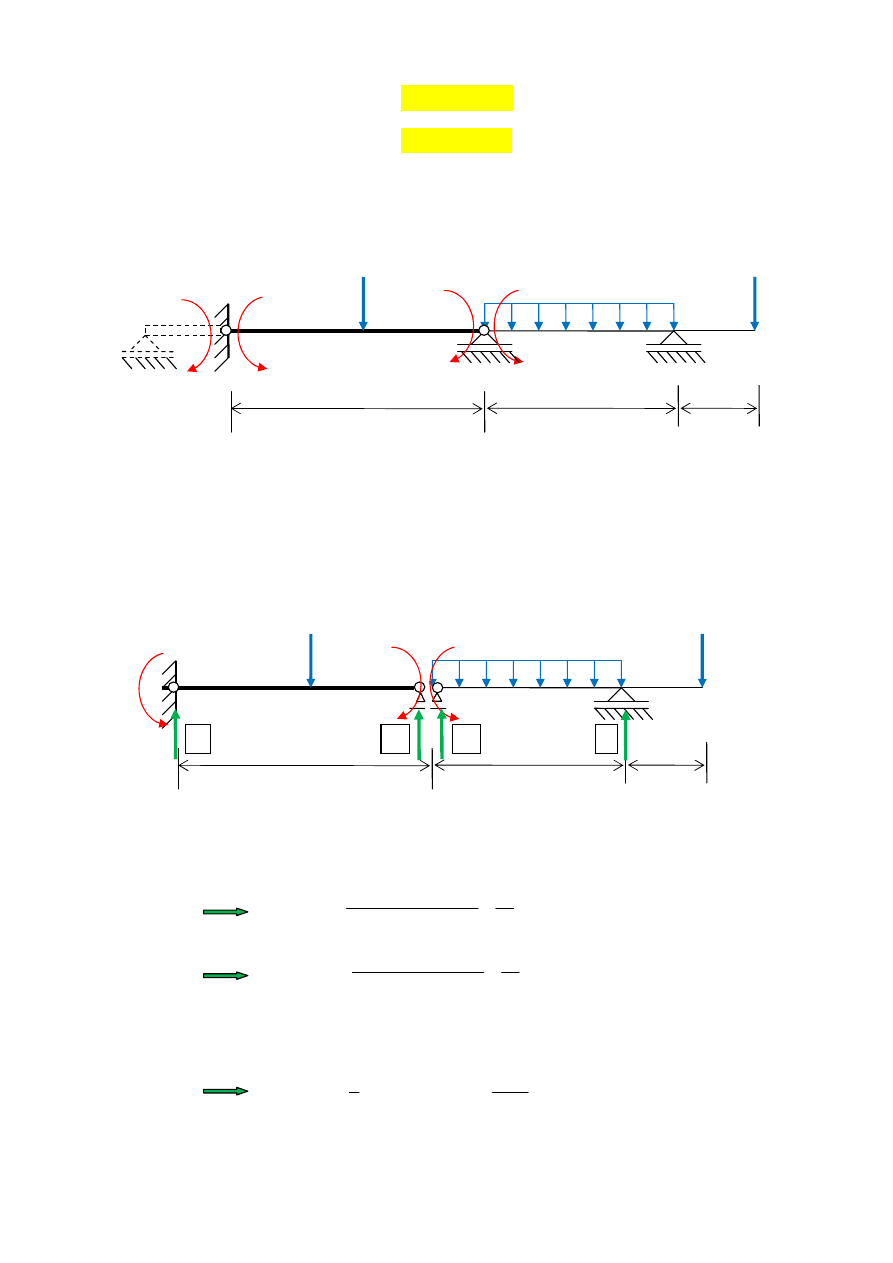
6. Wyliczenie pozostałych wielko
ś
ci statycznych - wykresy sił przekrojowych M i T
Rys. 10
Belk
ę
ci
ą
gł
ą
, po wyliczeniu
k
X
, mo
ż
emy dalej rozwi
ą
zywa
ć
jak dwie belki proste poł
ą
czone ze sob
ą
w
w
ęź
le „2” przegubem, w którym przyło
ż
one s
ą
wyliczone momenty przypodporowe
2
X
(rys. 11). Nast
ę
p-
nie w tych beleczkach liczymy reakcje podporowe i rysujemy wykresy T i M (rys. 12 i 13).
Rys. 11
Rozpatrujemy beleczk
ę
1-2:
∑
=
0
2
L
M
98
,
6
2
12
12
1262
,
26
8952
,
37
1
≅
+
−
=
V
∑
=
0
1
M
02
,
5
2
12
12
8952
,
37
1262
,
26
2
≅
+
−
=
L
V
Rozpatrujemy beleczk
ę
2-4:
∑
=
0
2
P
M
98
,
28
2
8
6
1262
,
26
11
6
8
1
2
3
≅
⋅
+
−
⋅
=
V
1
2
3
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 [m]=a
4
X
1
=37,8952
X
2
=26,1262
1
V
L
V
2
P
V
2
3
V
1
2
3
P
1
=12 kN
P
2
=6 kN
q=6 kN/m
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 [m]=a
4
0
X
1
=37,8952
X
2
=26,1262
Strona
9 z 9
∑
=
0
3
M
02
,
25
3
6
2
8
6
1262
,
26
8
1
2
2
≅
⋅
−
⋅
+
=
P
V
Sprawdzenie:
∑
=
0
y
P
0
6
8
6
12
02
,
25
98
,
28
02
,
5
98
,
6
=
−
⋅
−
−
+
+
+
c.n.d.
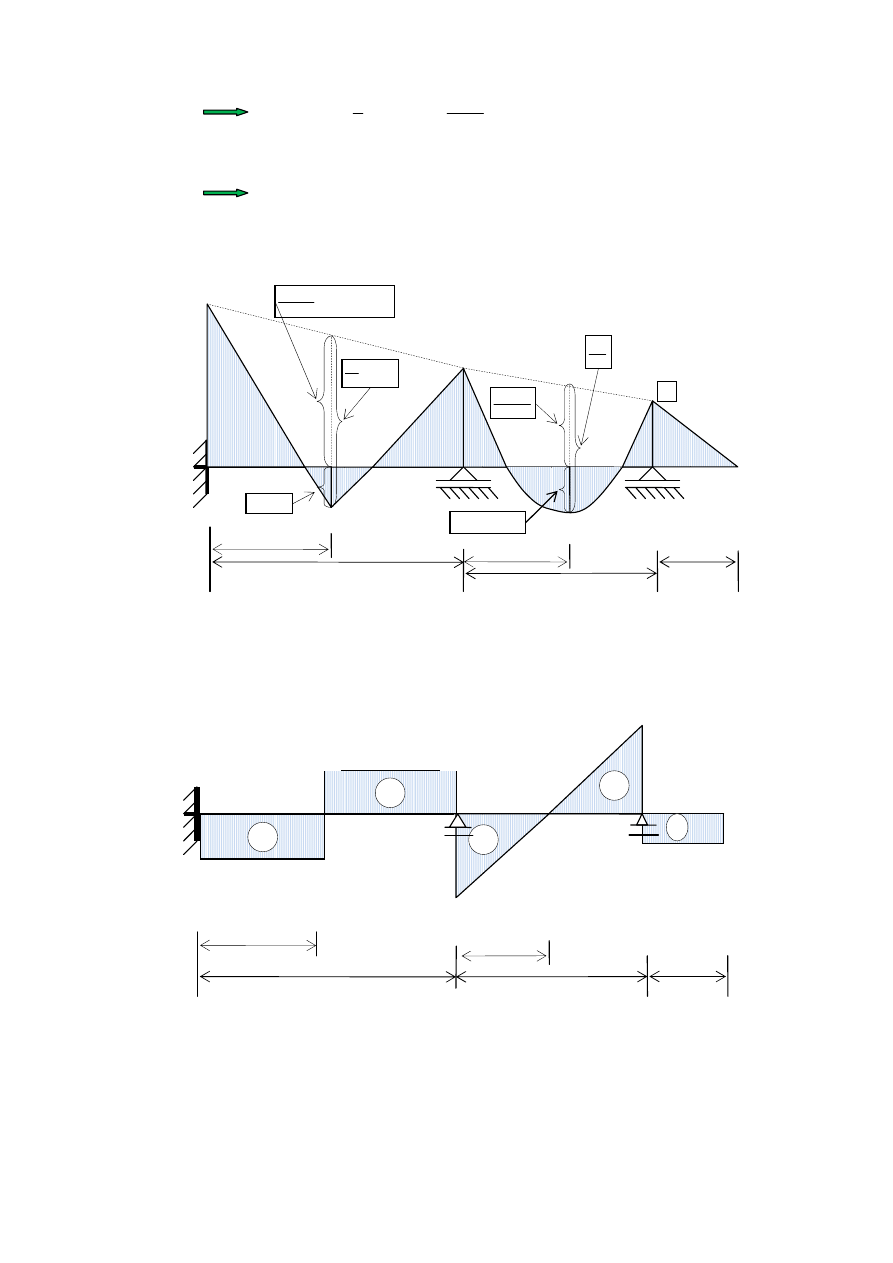
Rys. 12. Wykres momentów zginaj
ą
cych
Rys. 13. Wykres sił tn
ą
cych
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 [m]
6 [m]
6,98
x
≅
4,169
+
+
+
-
-
6,98
5,02
5,02
25,02
22,98
6
6
l
2
=12 [m]
l
3
=8 [m]
l
4
=3 [m]
X
1
=37,8952
X
2
=26,1262
6 [m]
3,9893
M
extr
≅
26,023
18
x
≅
4,169
0107
,
32
2
2
1
=
+
X
X
36
4
=
Pl
2
3
2
X
X
+
8
2
ql
Wyszukiwarka
Podobne podstrony:
metoda trzech mom - zad II, obc p -temp-osiad-styczeń 2011
Pomiary parametrów dwójników pasywnych metodą trzech woltomierzy
Usuwanie Cr(III) ze ścieków metodą biosorpcji, Studia, Studia II-stopień, Ochrona środowiska, Labora
zad II 17
PROTOKOL3 METRO ELEK Pomiary parametrów dwójników metodą trzech woltomierzy
metoda trzech momentow styczen 2011 id 291566
Metoda Vojty(1), STUDIA, KINEZYTERAPIA, II ROK
SPRAWOZDANIE3 METRO ELEK Pomiary parametrów dwójników metodą trzech woltomierzy
instr zad II
Metoda trzech wałeczków
ZAD II FINANSOWA, PŁ Matematyka Stosowana - licencjat, III semestr, Matematyka Finansowa i Ubezpiecz
Metoda typograficzna, INIB rok II, TiM
Metoda trzech równań podsumowanie
Ćw3 Pomiary parametrów dwójników pasywnych metodą trzech woltomierzy
mat bud - kruszywo metoda iteracji [poprawione], Studia, II rok, Materiały Budowlane 2
Badania i metoda statystyczna, INIB rok II, TiM
więcej podobnych podstron