Punkty pomiarowe

Interpolacja

p

j

‐ kilka funkcji przybliżających
‐ funkcje przechodzą przez wszystkie punkty  pomiarowe
‐ niewielka liczba punktów pomiarowych 

Aproksymacja
‐ jedna funkcja przybliżająca

funkcja przechodzi tak aby błąd przybliżenia punktów

‐ funkcja przechodzi tak aby błąd przybliżenia  punktów 

pomiarowych był jak najmniejszy

‐ znaczna liczba punktów pomiarowych

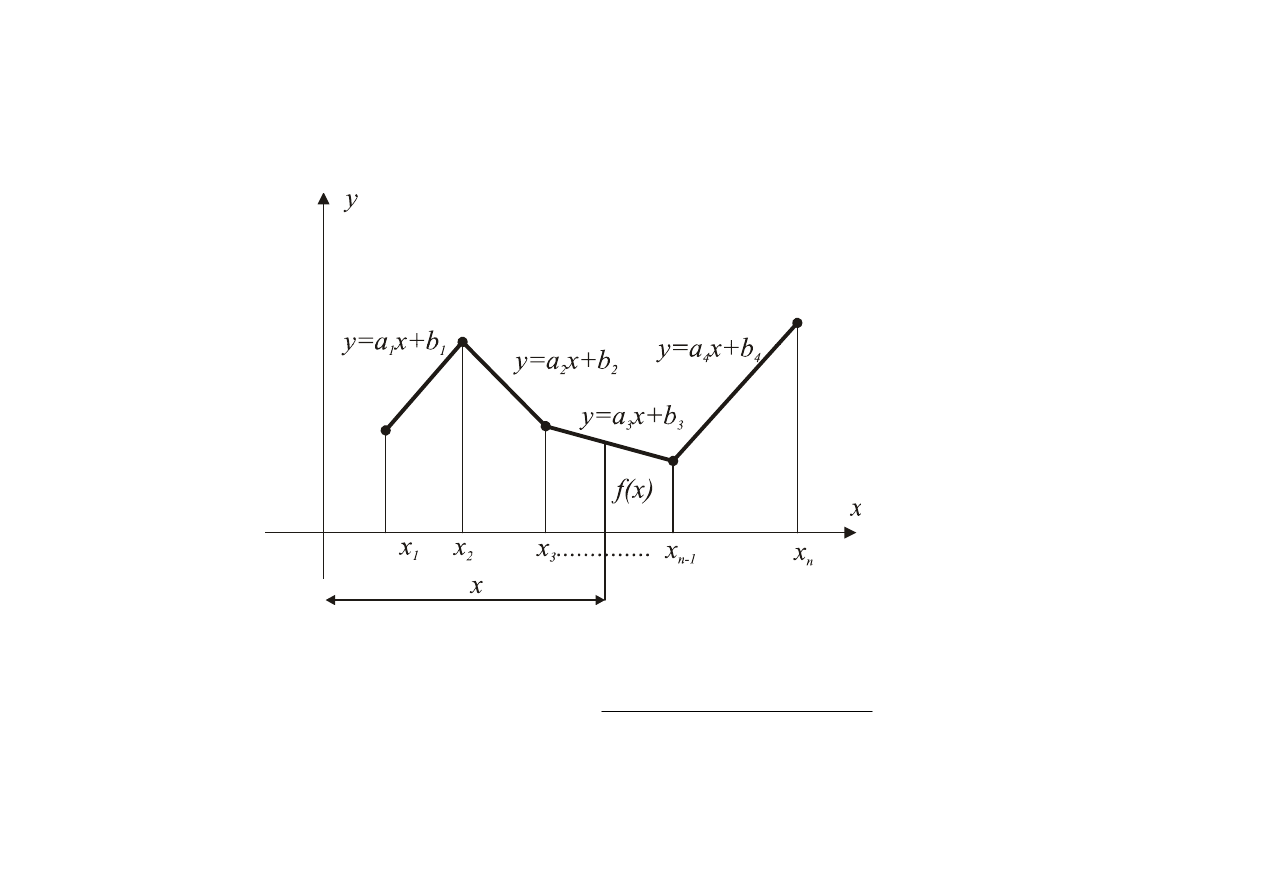
Interpolacja liniowa

 





 







1

1

1

1

n

n

n

n

f x

f x

f x

f x

x x

x

x

















1

n

n

x

x



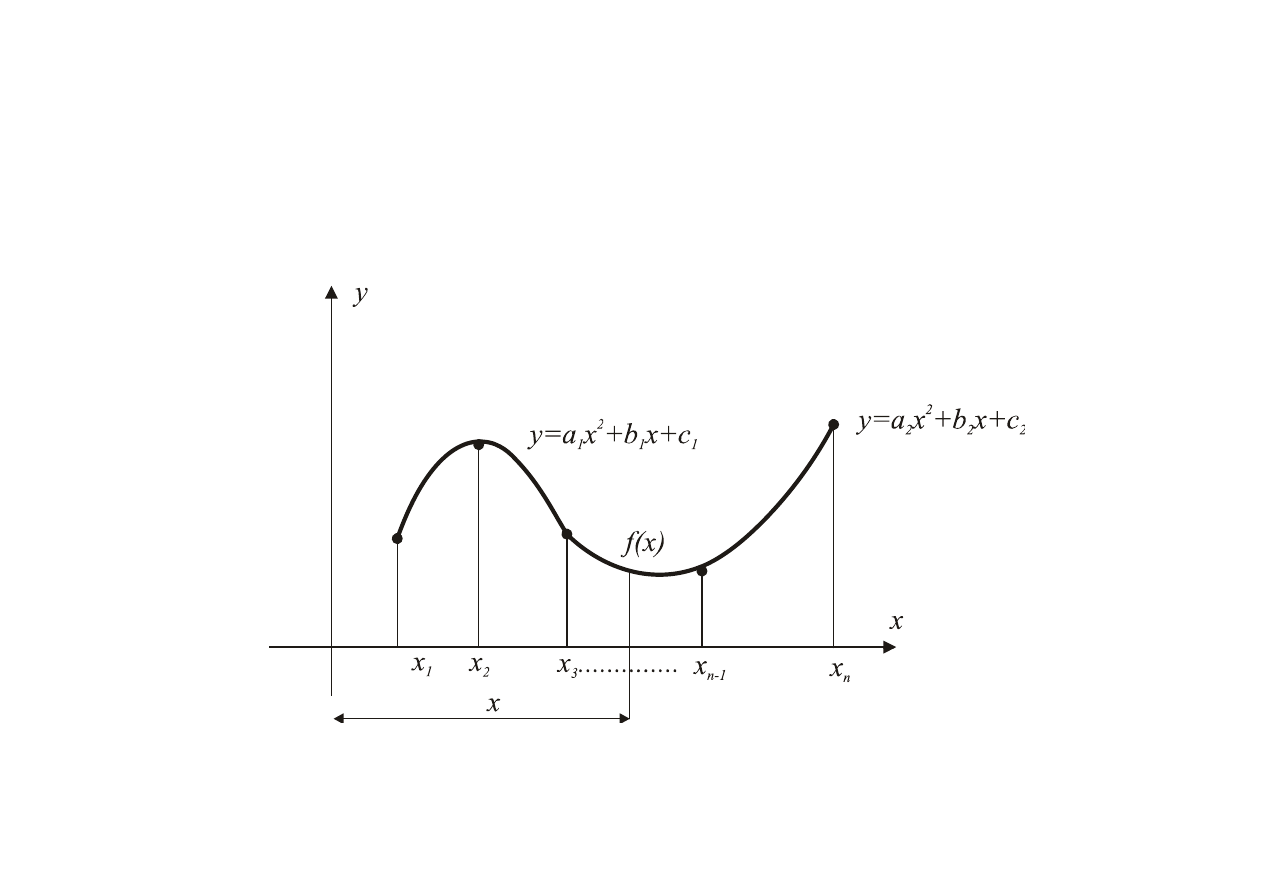
Interpolacja kwadratowa

 











f

b

b

b

 











0

1

1

2

1

n

n

n

f x

b

b x x

b x x

x x





 













0

1

n

b

f x





 





1

n

n

f x

f x

b







 





1

1

n

n

b

x

x











 

 





1

1

n

n

n

n

f x

f x

f x

f x











1

1

2

1

1

n

n

n

n

n

n

x

x

x

x

b

x

x

















 

2

0

1

2

f x

a

a x a x







 

0

1

2

f x

a

a x a x





0

0

1

1

2

1

n

n

n

a

b

b x

b x x











1

1

2

1

2

n

n

a

b

b x

b x



 



2

2

a

b



Interpolacja wielomianowa dowolnego stopnia n

 















0

1

0

0

1

1

n

n

f x

b

b x x

b x x

x x

x x



 



 











 















 

0

0

b

f x



 

0

0

f





1

1

0

,

b

f x x







2

2

1

0

, ,

b

f x x x









1

1

0

,

,

, ,

n

n

n

b

f x x

x x











 

 

f x

f x



 

 

,

i

j

i

j

i

j

f x

f x

f x x

x

x



 







,

,

,

,

i

j

j

k

i

j

k

f x x

f x x

f x x x





















 





i

j

k

i

k

f

x

x





















1

1

1

2

0

,

,

,

,

,

,

n

n

n

n

f x x

x

f x

x

x

f x x

x x



















1

1

0

0

,

,

,

n

n

n

f x x

x x

x

x









Metoda kolokacji

Niech wartości funkcji                                      będą dane w punktach

Szukamy funkcji

w postaci kombinacji liniowej

1

2

,

,

,

n

y y

y



1

2

,

,

,

n

x x

x



 

y

f x



Szukamy funkcji                             w postaci kombinacji liniowej

 

y

f x



 

 

 

y a f x

a f x

a f x





 

 

 

 

1 1

2

2

n n

y a f x

a f x

a f x





 



Funkcje

są z góry założone

 

i

f x

Funkcje                       są z góry założone 

 

i

f x

Kolokacja wielomianowa

 

1

1, 2,

,

i

i

f x

x

i

n









Kolokacja szeregami Czebyszewa

 

 

1

1, 2,

,

i

i

f x

T

x

i

n









 





1

2

cos

1 arccos

i

x g d

T

x

i

d

x g

d



 









 









 





1

i

g

g d











 

0

1

T x



 

0

1

T x

 

2x

g d

T

 

 

1

g

T x

g d





Wzór rekurencyjny

Wzór rekurencyjny

 

   

 

1

1

1

2

k

k

k

T

x

T x T x

T

x









 

   

 

Kolokacja szeregami Fouriera

 

2

1

cos

1

0 1

k

f

x

kx

k

n





2

0, 1,

,

2

sin

k

k

n

f

kx







Rozwiązanie

 

 

 

1 1

2

2

n n

y a f x

a f x

a f x





 



 

 

 

1 1

2

2

n n

y

f

f

f

 

 

 

1 2

y

a f x

a f x

a f x

i

n





 



 

 

 

1 1

2

2

1, 2,

,

i

i

i

n n

i

y

a f x

a f x

a f x

i

n





 







Powstaje układ równań ze względu na parametry 

i

a

j

g ę

p

y

i

Dla funkcji wielu zmiennych









1 1

1

2

2

2

1

2

,

,

,

,

,

,

i

n

n

y

a f x x

x

a f x x

x























1

2

,

,

,

1 2

n n

n

a f x x

x

i







1, 2,

,

i

n





A

k

j

Aproksymacja

Sposoby aproksymacja ze względu na sposób liczenia błędu

y a

a x e

e y a

a x







0

1

0

1

y a

a x e

e y a

a x









 



Minimum sumy błędów

n

n





0

1

1

1

i

i

i

i

i

e

y

a

a x















Minimum sumy wartości bezwzględnych błędów

0

1

n

n

i

i

i

e

y

a

a x











0

1

1

1

i

i

i

i

i

e

y

a

a x









Kryterium „minimax” –minimum największego błędu

1

2

min(max( ,

,

,

))

n

e e

e



Minimum sumy kwadratów – metoda najmniejszych kwadratów





2

2

n

n

S









2

2

0

1

1

1

r

i

i

i

i

i

S

e

y

a

a x

















Metoda najmniejszych kwadratów – opis ogólny

Wartości funkcji                                        dane są w punktach

Szukamy funkcji jako kombinacji liniowej pewnych funkcji

1

2

,

,

,

n

y y

y



1

2

,

,

,

n

x x

x



Szukamy funkcji jako kombinacji liniowej pewnych funkcji

 

 

 

1 1

2 2

l l

y a f x

a f x

a f x





 



Znanych funkcji 

 

 

 

1

2

,

,

,

l

f x

f x

f x



Różnica: 

l

n



Błąd i‐tego równania

 

 

 

1 1

2 2

i

i

i

i

l l

i

y

y

a f x

a f x

a f x

  



 



 

 

 

współczynniki           dobieram tak, aby błąd był najmniejszy

i

a

p

y

,

y

ą

y

j

j y

i

2

 

2

2

1

1

1

min

n

n

l

r

i

i

k k

i

i

i

k

S

y

y

a f x











  



















1

1

1

i

i

k





 

 

1

1

2

0

1, 2,

,

n

l

r

i

k k

i

j

i

i

k

j

S

y

a f x

f x

j

l

a









 

































1

1

i

k

j





P

t j

kł d l ó

ń l i

i d

i

Powstaje układ  l równań z l niewiadomymi

1

1 2

l

jk k

j l

c a

c

j

l







, 1

1

1, 2,

,

jk k

j l

k

c a

c

j

l









n

   

1

n

jk

kj

k

i

j

i

i

c

c

f x f x









 

, 1

1

,

1, 2,

,

n

j l

i

j

i

i

c

y f x

k j

l













i

Kontrola błędu 

Wariancja

2

, 1

n

l

t

i

k k l

S

y

a c











Odchylenie standardowe

,

1

1

i

k





Odchylenie standardowe









y

t

s

S

n l





Metoda najmniejszych kwadratów (regresja lub aproksymacja liniowa)

0

1

0

1

y a

a x e

e y a

a x









 







2

2

0

1

1

1

n

n

r

i

i

i

i

i

S

e

y

a

a x





















0

1

0

2

0

r

i

i

S

y

a

a x

a



 



















0

1

1

2

0

r

i

i

i

S

y

a

a x x

a



 











0

1

2

0

0

i

i

y

a

a x





















2

0

1

0

0

0

i i

i

i

y x

a x

a x

a

na

















0

1

i

i

na

x a

y













2

0

1

i

i

i i

x a

x a

x y















Rozwiązanie





1

2

2

i

i

i

n

x y

x

y

a







 









2

2

1

1

0

1

i

i

i

i

n

n

n

x

x

a

y a x

y

y

x

x



 













n

n





Statystyczna ocena rozwiązania

wartość średnia i i kwadrat odchyleń 





2

1

i

t

i

n

y

y

S

y

y











odchylenie standardowe i wariancja

y

j

2

1

1

t

t

y

y

S

S

s

s

n

n









1

1

n

n

współczynnik wariacji

100%

y

s

c. v.

100%

y

y



standardowy błąd przybliżenia (    

), współczynnik determinacji (r

2

), 

/

y x

s

współczynnik korelacji (r)

2

1

t

r

r

S

S

S

i

i d kł d



y

2

/

1

2

t

r

r

y x

t

s

r

r

rozwiązanie dokładne

n

S





 



Rozwiązanie poprawne gdy 

/

y x

y

s

s

