Mechanika i wytrzymałość materiałów

WPPT

Materiały dla studentów

Doświadczalne wyznaczanie masowego momentu bezwładności.

Mgr inż. Monika Stefańska

Wrocław 2009

All rights reserved

1.

Wprowadzenie

Bryła sztywna

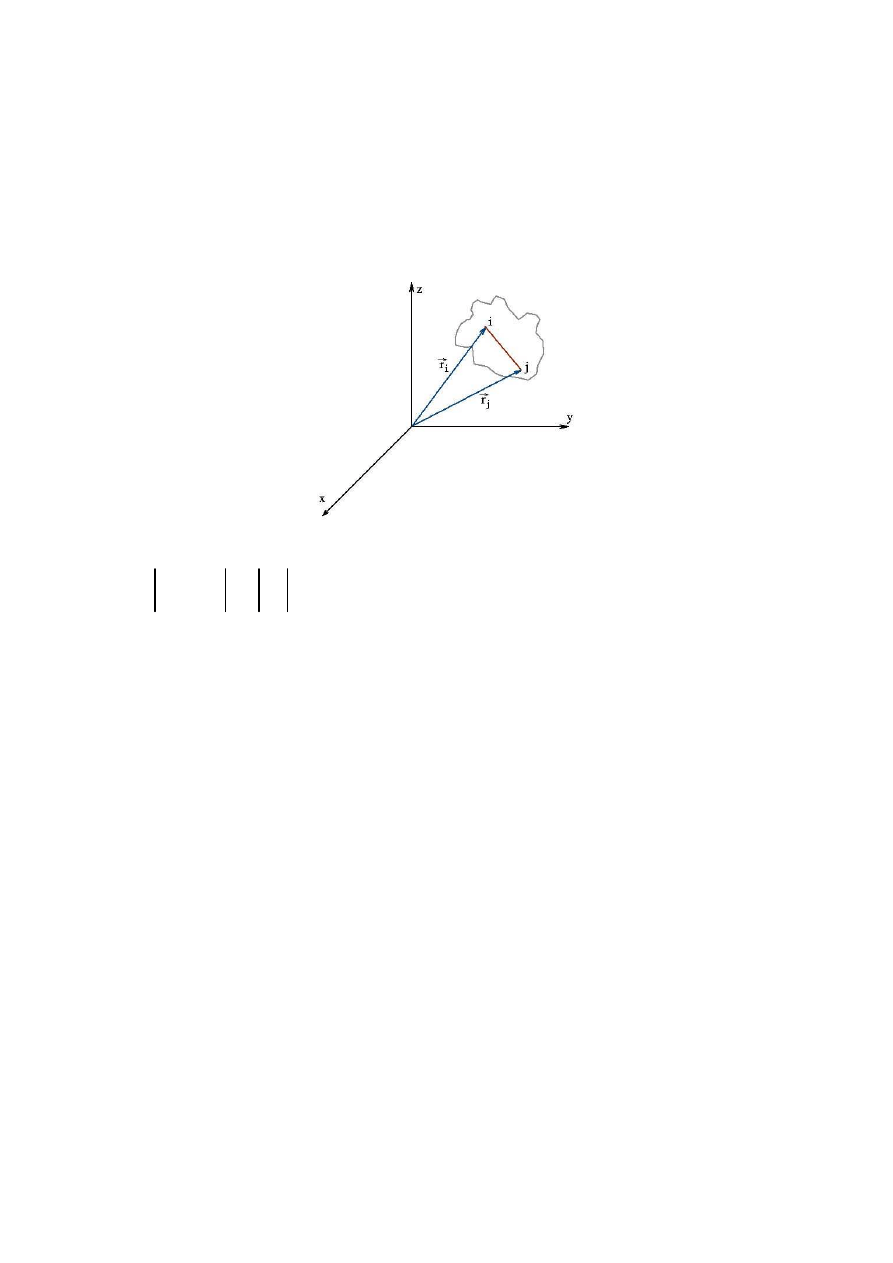
Bryłą sztywną nazywamy takie ciało, w którym wszystkie punkty mają zawsze względem
siebie stałą odległość.

Rys. 1 Bryła sztywna

i

j

ij

ij

r

r

r

r

− =

=

⇒

r

r

r

nie zależy od czasu

Stąd wynika, ze podczas ruchu układ punktów materialnych składających się na bryłę
sztywną porusza się jako całość o nie zmieniającej się postaci i objętości.

Moment bezwładności

Do opisu ruchu obrotowego brył sztywnych wprowadzono pojęcie momentu bezwładności,
który w tym przypadku jest miarą bezwładności, podobnie jak masa w ruchu postępowym.
Jest to spowodowane tym, że w ruchu obrotowym bryły znaczenie ma nie tylko masa, ale i jej
rozkład względem osi obrotu. Ruch obrotowy całej bryły można rozpatrywać jako sumę
ruchów po okręgu poszczególnych mas elementarnych, na które można podzielić całą bryłę.

Moment bezwładności to wielkość charakteryzująca bezwładność ciała stosowana przy
opisie ruchu obrotowego.

Jeżeli na bryłę poruszającą się ruchem obrotowym działa moment siły M, to bryła porusza się
z przyspieszeniem kątowym ε, którego wartość jest proporcjonalna do wartości momentu siły
i odwrotnie proporcjonalna do momentu bezwładności bryły:

ε=M/I

(1)

Równanie (1) wyraża treść II zasady dynamiki dla ruchu obrotowego.

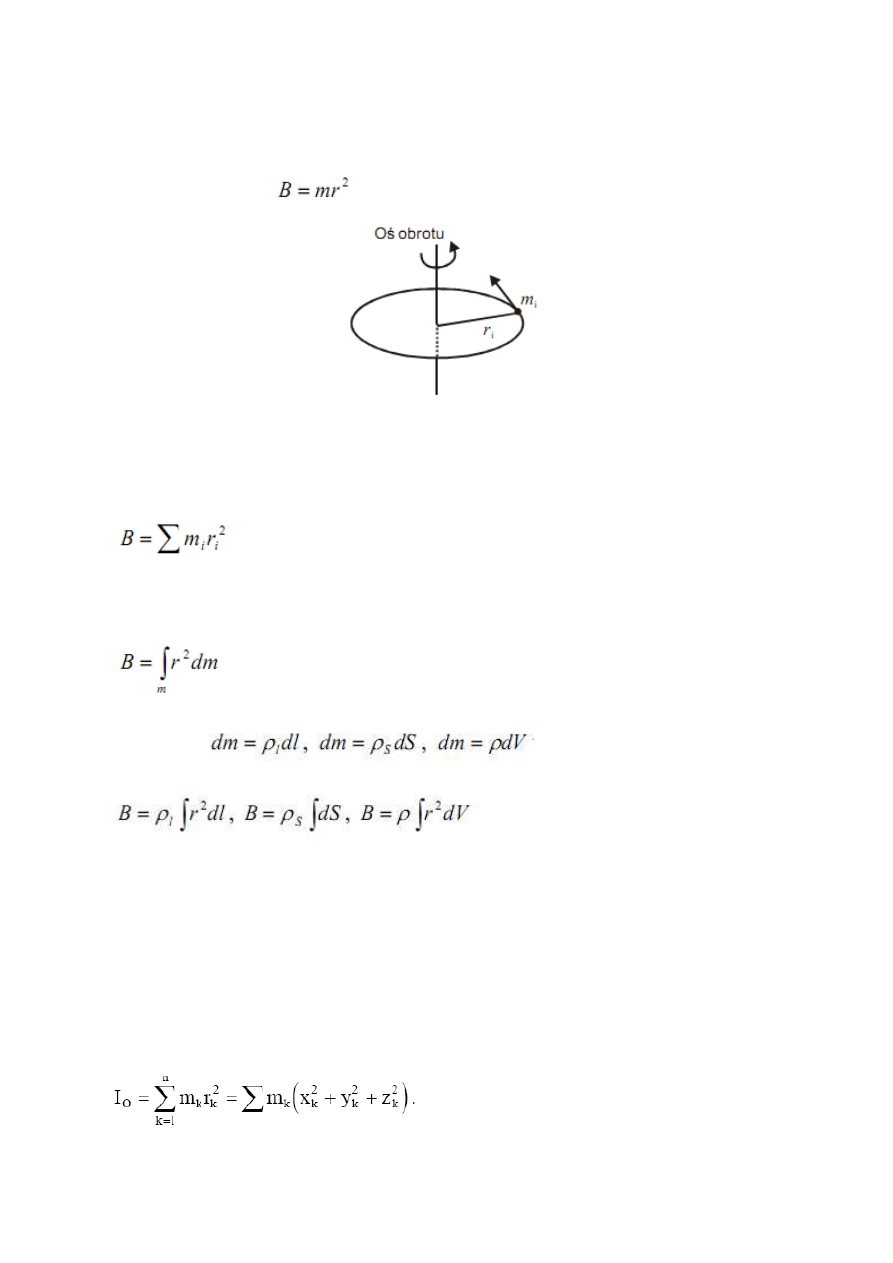
Momentem bezwładności punktu materialnego względem płaszczyzny, osi lub bieguna
nazywamy iloczyn masy punktu przez kwadrat odległości tego punktu od danej płaszczyzny,
osi lub bieguna:

(2)

Rys.2 Moment bezwładności punktu materialnego względem osi

Momentem bezwładności układu punktów materialnych względem płaszczyzny, osi lub
bieguna nazywamy sumę momentów bezwładności wszystkich punktów materialnych
względem tej płaszczyzny, osi lub bieguna:

(3)

Momentem bezwładności układu ciągłego (linii, powierzchni lub bryły materialnej)
względem przyjętej płaszczyzny osi lub bieguna nazywamy całkę:

(4)

Podstawiając

zależności od tego, czy układ jest

linią, powierzchnią, czy bryłą materialną, otrzymujemy dla ciał jednorodnych (p= const):

Całki występujące po prawej stronie równań nazywamy geometrycznymi momentami
bezwładności. Masowy moment bezwładności jest więc (dla ciał jednorodnych) iloczynem
gęstości przez geometryczny moment bezwładności.

Dla danego układu ciągłego można wyróżnić momenty bezwładności względem trzech
płaszczyzn współrzędnych, trzech osi współrzędnych i bieguna.

Biegunowym momentem bezwładności I

O

układu punktów materialnych względem punktu O

nazywamy sumę iloczynów mas m

k

i kwadratów ich odległości od punktu 0, czyli:

(5)

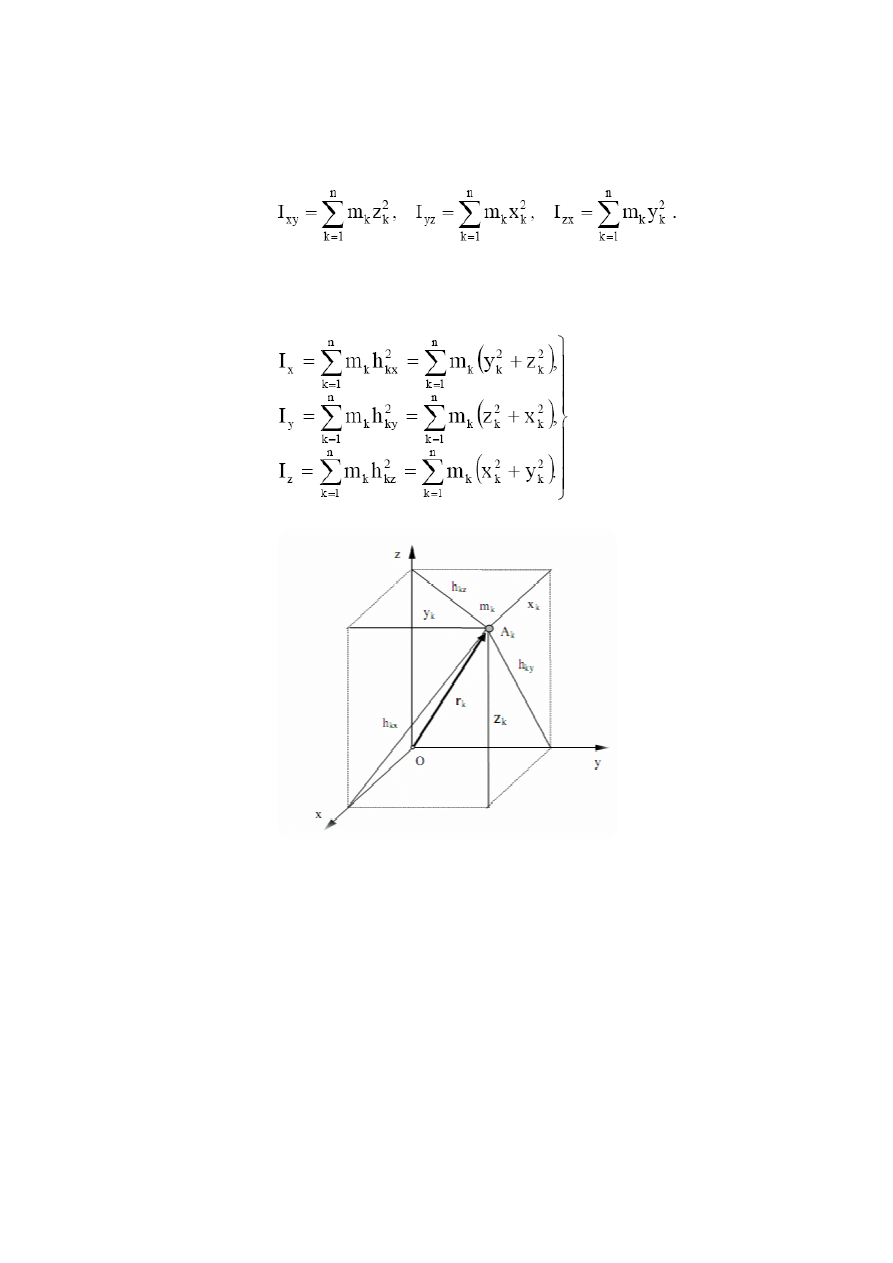
Momentami bezwładności I

xy

materialnych nazywamy sumy iloczynów mas m

płaszczyzn. Zatem mamy:

Momentami bezwładności I

x

, I

y

sumy iloczynów mas m

k

oraz kwadratów ich odległo

Rys. 3

Pomiędzy tymi momentami zachodz
• Suma momentów bezwładno
jest równa momentowi bezwładno
przecięcia się tych płaszczyzn.
• Biegunowy moment bezwładno
bezwładności względem trzech prostopadłych osi przechodz
• Moment biegunowy jest sum
przechodzących przez dany biegun.

xy

, I

yz

, I

zx

względem płaszczyzn xy, yz, zx uk

materialnych nazywamy sumy iloczynów mas m

k

przez kwadraty ich odleg

y

, I

z

względem osi x, y, z układu punktów materialnych nazywamy

oraz kwadratów ich odległości od tych osi:

Rys. 3 Opis położenia punktu materialnego

dzy tymi momentami zachodzą następujące związki:

• Suma momentów bezwładności względem dwóch płaszczyzn wzajemnie prostopadłych

ówna momentowi bezwładności względem osi pokrywającej si

tych płaszczyzn.

• Biegunowy moment bezwładności jest równy połowie sumy osiowych momentów

dem trzech prostopadłych osi przechodzących przez ten biegun.

sumą momentów względem trzech prostopadłych płaszczyzn

cych przez dany biegun.

xy, yz, zx układu punktów

przez kwadraty ich odległości od tych

(6)

x, y, z układu punktów materialnych nazywamy

(7)

dem dwóch płaszczyzn wzajemnie prostopadłych

cej się z krawędzią

ci jest równy połowie sumy osiowych momentów

cych przez ten biegun.

dem trzech prostopadłych płaszczyzn

Oprócz tych szczególnych momentów bezwładno
nieskończenie dużo momentów bezwładno
bieguna.

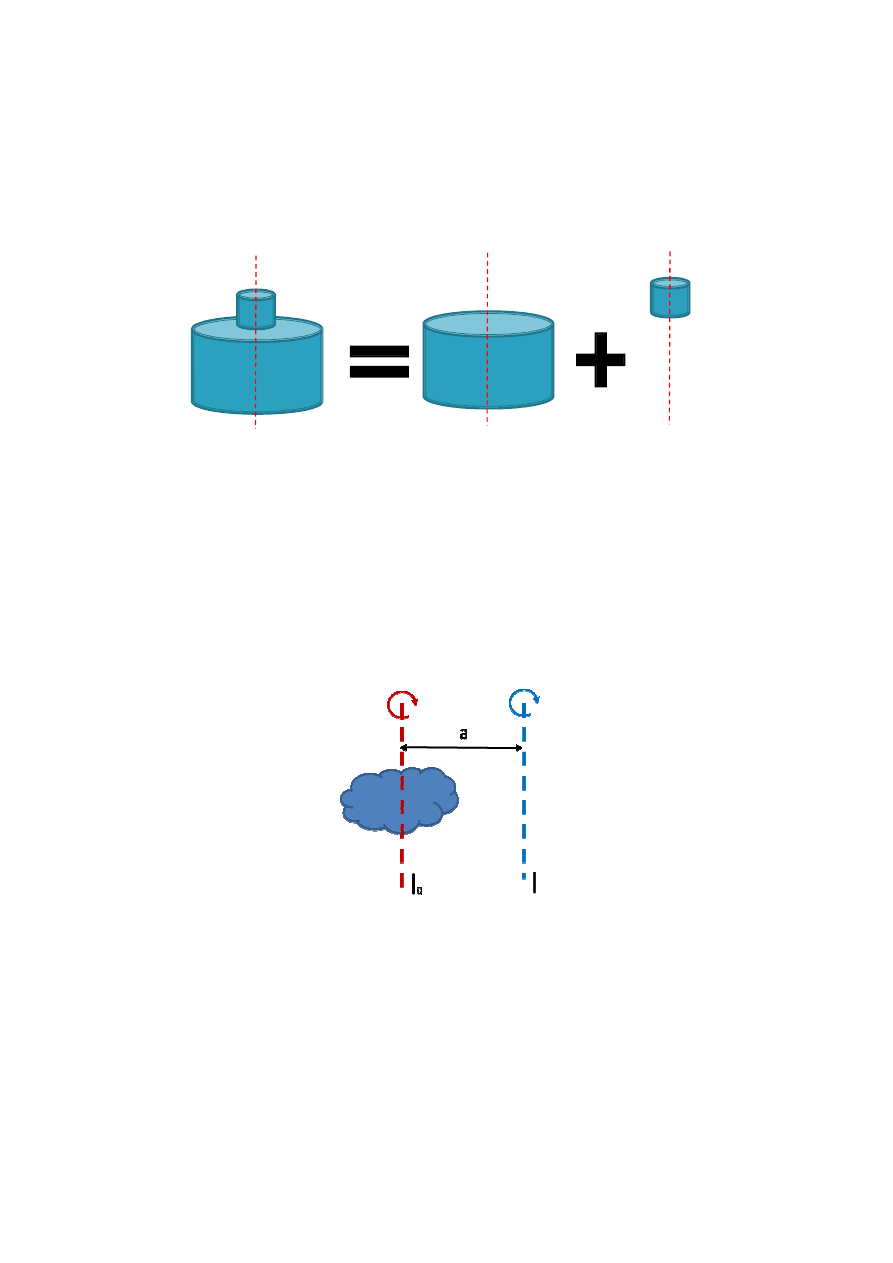
Bardzo ważną własnością momentów bezwładno
jest addytywność (rys.4).

Rys.4 Addytywno

Twierdzenie Steinera

Moment bezwładności wzglę
równoległej przechodzącej przez
układu przez kwadrat.

2

a

m

I

I

o

⋅

+

=

Tensor bezwładności

Analizując dynamikę ciała stałego mog
potrzebna jest znajomość pełnego rozkładu masy, który to rozkład wyra
bezwładności ciała sztywnego. Tensor bezwładno
związanym z ciałem. Tensor bezwładno
masy ciała sztywnego względem osi konkretnego układu współrz
związanego z ciałem. Ogólnie tensor bezw

I

1+2

ócz tych szczególnych momentów bezwładności, dowolny układ materialny ma

o momentów bezwładności, w zależności od obioru płaszczyzny, osi lub

ą momentów bezwładności wynikającą bezpośrednio z ich defini

Rys.4 Addytywność momentów bezwładności

ci względem dowolnej osi jest równy momentowi wzgl

cej przez środek ciężkości powiększonemu o iloczyn masy całkowitej

Rys.5 Twierdzenie Steinera

ciała stałego mogącego obracać się wokół dowolnej osi w przestrzeni

pełnego rozkładu masy, który to rozkład wyrażamy poprzez tensor

ci ciała sztywnego. Tensor bezwładności określany jest w układzie współrz

zanym z ciałem. Tensor bezwładności jest więc zbiorem wielkości definiuj

ędem osi konkretnego układu współrzędnych, najcz

zanego z ciałem. Ogólnie tensor bezwładności wyrażamy w postaci macierzy:

I

1

ci, dowolny układ materialny ma

obioru płaszczyzny, osi lub

średnio z ich definicji

dem dowolnej osi jest równy momentowi względem osi

kszonemu o iloczyn masy całkowitej

(8)

wokół dowolnej osi w przestrzeni

pełnego rozkładu masy, który to rozkład wyrażamy poprzez tensor

lany jest w układzie współrzędnych

ci definiujących rozkład

dnych, najczęściej układu

amy w postaci macierzy:

I

2

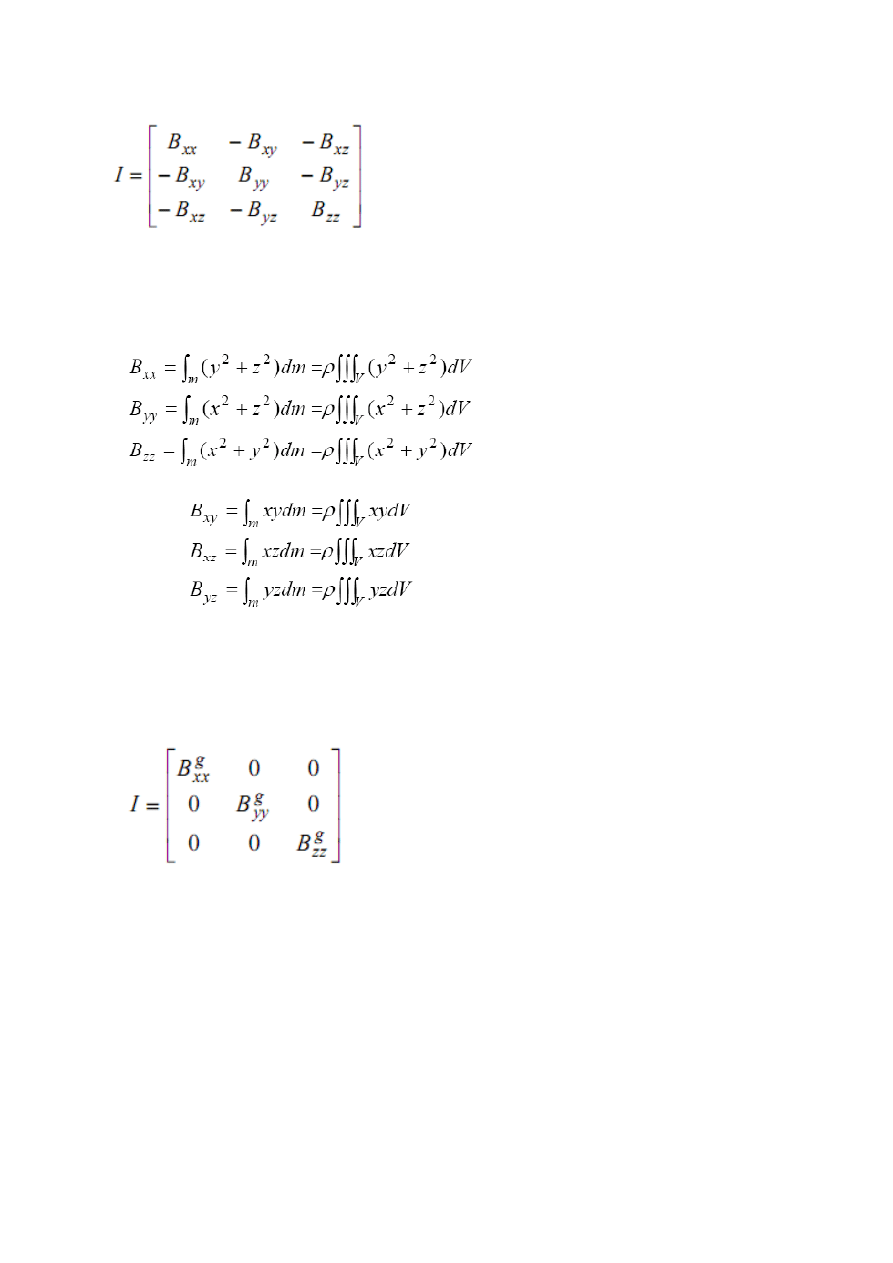
(9)

gdzie: Bxx, Byy, Bzz – momenty bezwładności ciała względem poszczególnych osi układu
współrzędnych, Bxy, Byz, Byz – momenty dewiacyjne (odśrodkowe) bezwładności,
wyznaczane względem poszczególnych płaszczyzn układu współrzędnych.

(10)

Współrzędne tensora bezwładności zależą od położenia i orientacji układu współrzędnych
względem zapisujemy tensor bezwładności ciała. Dobierając orientację układu współrzędnych
tak by jego osie pokrywały się z głównymi osiami bezwładności ciała uzyskujemy
wyzerowanie odśrodkowych momentów bezwładności.

(11)

Doświadczalne metody wyznaczania masowego momentu bezwładności

Doświadczalne wyznaczanie momentów bezwładności jest metodą stosowaną w przypadkach
ciał o nieregularnych kształtach, których momenty bezwładności nie jest łatwo wyznaczyć
metodami analitycznymi czyli metodami opartymi na wymiarach geometrycznych ciał.
Wykorzystując powyżej wspomniane definicje i twierdzenia można łatwo wyznaczyć masowe
momenty bezwładności części maszyn o kształtach regularnych. Jednak dla wielu elementów
o kształtach skomplikowanych (np. korbowód, wal korbowy, koło zębate) często
występujących w praktyce, zastosowanie ich prowadzi do bardzo skomplikowanych obliczeń.
Wtedy odwołujemy się do metod doświadczalnych.

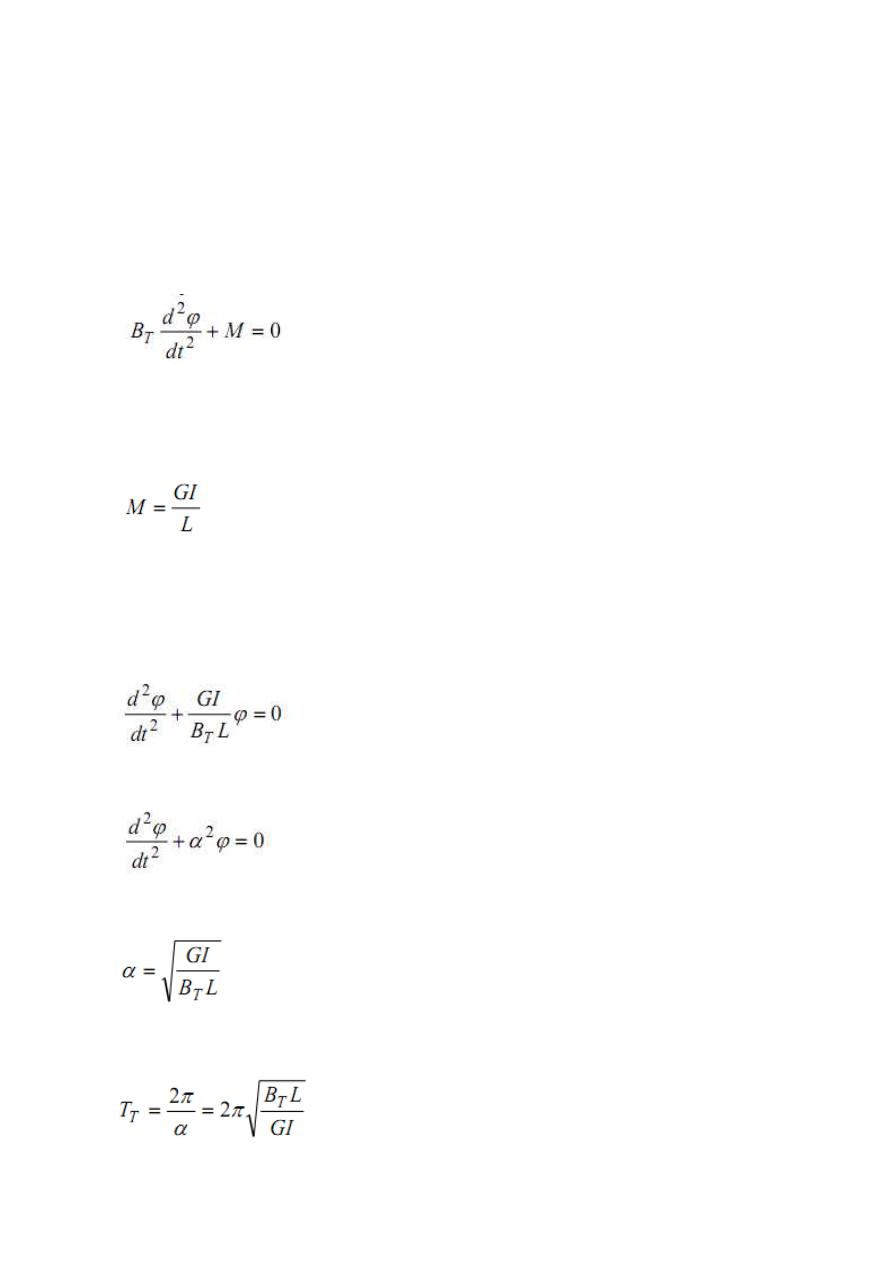
Metoda zawieszenia jednonitkowego

Stanowisko pomiarowe składa się ze stojaka, na którym zawieszona jest na strunie stalowej
tarcza. Na tarczy można umieszczać badane ciało. Załóżmy niewielkie, do 10 stopni,
wychylenia skrętne tarczy z położenia równowagi opisane zmienną

ϕ. Ζgodnie z drugą

zasadą Newtona równanie różniczkowe ruchu tarczy ma wówczas postać

(12)

gdzie: B

T

– moment bezwładności tarczy względem osi struny, M – moment reakcyjny

związany ze skręceniem struny. Moment ten jest liniowo zależny od kąta skręcenia struny

ϕ i

ma postać:

(13)

gdzie: G – moduł sprężystości postaciowej struny (własność materiału z którego wykonana
jest struna), I – biegunowy moment bezwładności kołowego przekroju poprzecznego struny,
L – długość struny.

Wstawiając równanie (13) do równania (12) otrzymujemy:

(14)

Ogólnie równanie (14) drgań tarczy możemy wyrazić jako:

(15)

Częstość kołowa drgań własnych tarczy wynosi więc:

(16)

natomiast okres drgań:

(17)

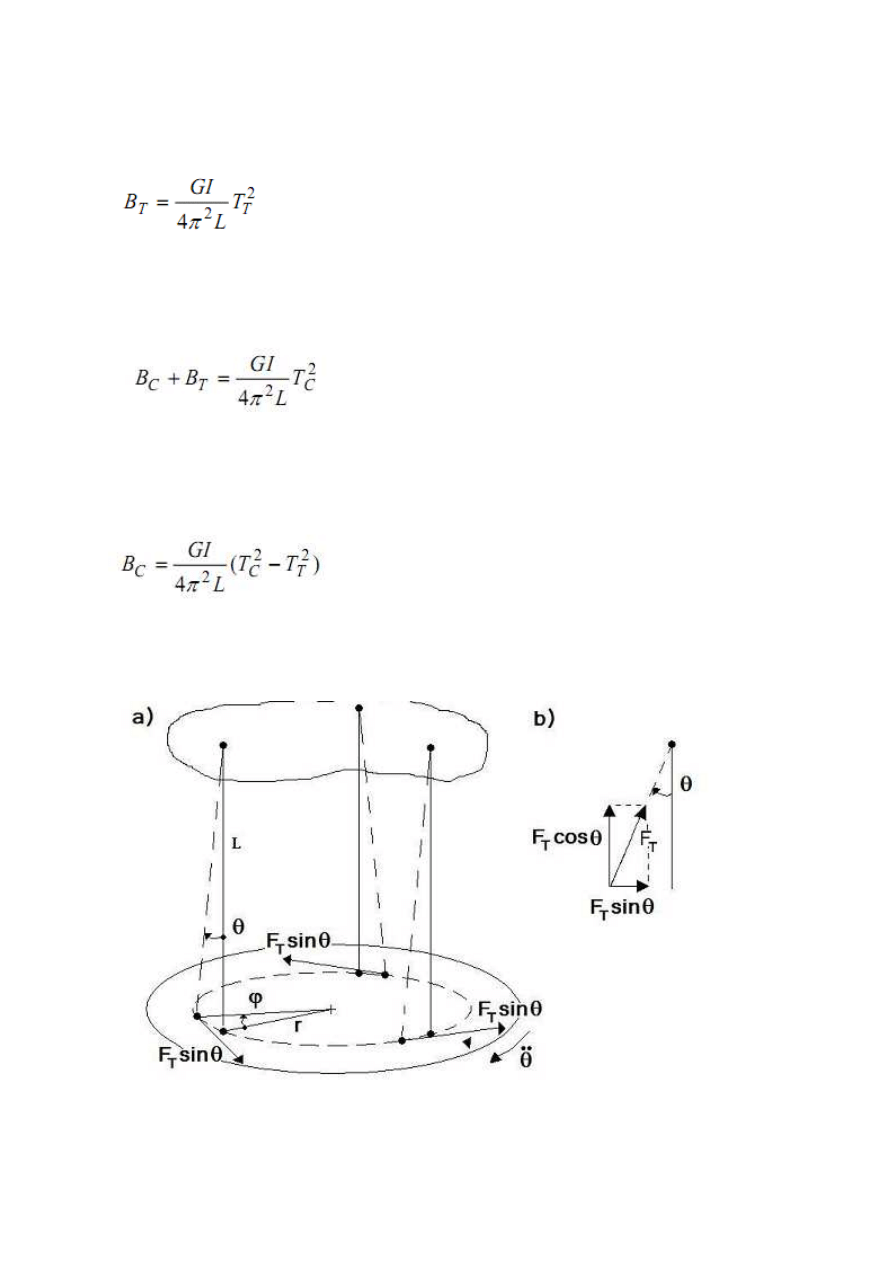
Przekształcając równanie (17) możemy wyznaczyć moment bezwładności tarczy względem
pionowej osi obrotu (czyli struny) :

(18)

Jak widzimy we wzorze (18) wyrażenie GI/4π

2

L jest wartością stałą. Umieszczając na tarczy

badany obiekt w taki sposób by środek masy obiektu leżał na linii osi obrotu tarczy z członem
uzyskujemy

(19)

gdzie: B

C

– moment bezwładności obiektu względem osi obrotu tarczy, T

C

- okres drgań

skrętnych tarczy z umieszczonym na niej obiektem.

Podstawiając (18) do (19) mamy:

(20)

Metoda zawieszenia trójnitkowego

Rys. 6 a) Stanowisko pomiarowe b) rozkład siły napięcia nici na składowe

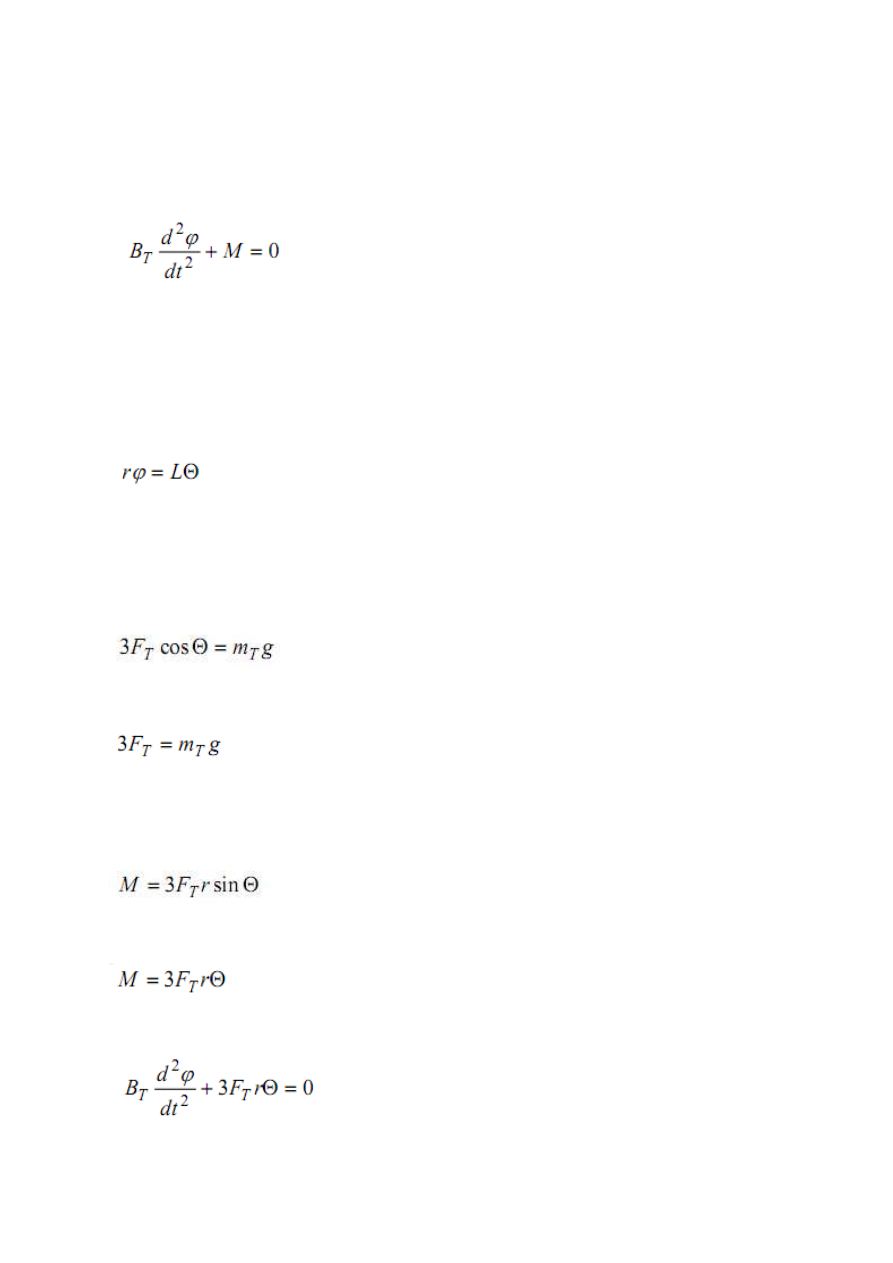
Stanowisko pomiarowe składa się ze stojaka, na którym zawieszona jest na trzech nitkach o
jednakowej długości tarcza, Rys. 6. Na tarczy można umieszczać badane ciało. Załóżmy
niewielkie, do 10 stopni, wychylenia skrętne tarczy z położenia równowagi opisane zmienną
ϕ. Ζgodnie z drugą zasadą Newtona równanie różniczkowe ruchu tarczy ma wówczas postać:

(21)

gdzie: BT – moment bezwładności tarczy względem osi pionowej, M – moment sił
działających na tarczę. Równanie (21) opisuje skrętne drgania własne nietłumione tarczy.

Wychyleniu kątowemu tarczy

ϕ wokół pionowej osi przechodzącej przez jej środek masy

odpowiada obrót nici zawieszenia tarczy o kąt θ, Rys. 6a. Możemy więc zapisać zależność
obu kątów jako:

(22)

gdzie: r – promień mierzony od środka tarczy do punktu zamocowania nici, L – długość nici.

Rozważając dowolne skrętne wychylenie tarczy z położenia równowagi możemy siłę napięcia
nici F

T

, Rys. 6b, wyrazić poprzez składową pionową F

T

cosθ oraz poziomą F

T

sinθ. Rzutując

wszystkie siły działające na tarczę na kierunek pionowy otrzymujemy:

, gdzie: m

T

– masa tarczy.

(23)

Pamiętając o założeniu małych kątowych wychyleń tarczy θ < 10 równanie (23) ma postać:

(24)

Z kolei składowa pozioma siły naprężenia nici jest siłą styczną do promienia okręgu
zamocowania wszystkich trzech nici. Możemy więc moment sił działających na tarczę
względem osi pionowej przechodzącej przez środek masy tarczy zapisać jako:

(25)

dla θ < 10 równanie (25) przyjmuje postać:

(26)

Wstawiając równanie (26) do równania (21) otrzymujemy:

(27)

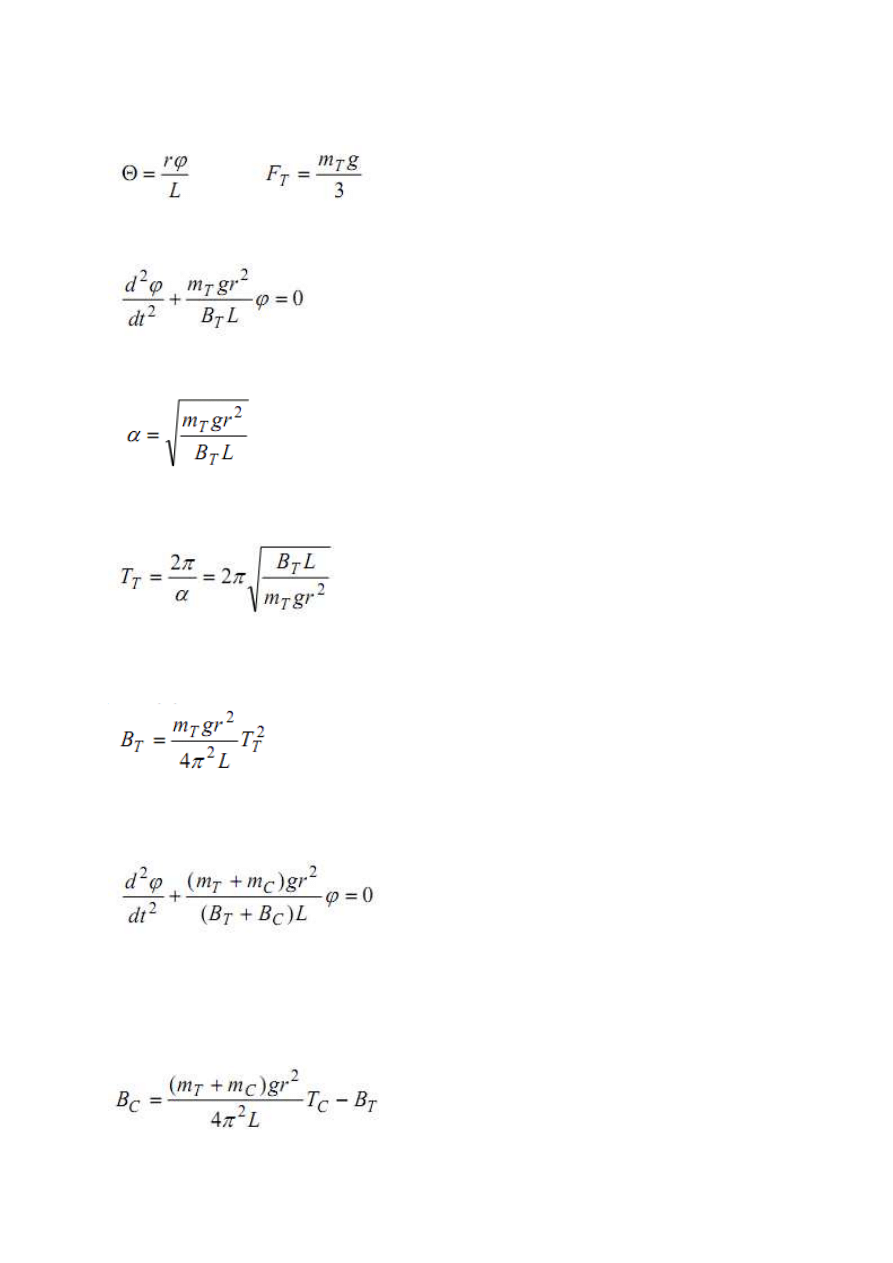
Z równań (22) oraz (24) mamy:

(28)

Podstawiając równanie (28) do (27) otrzymujemy równanie drgań tarczy w postaci:

(29)

Częstość kołowa drgań własnych tarczy wynosi więc:

(30)

natomiast okres drgań:

(31)

Przekształcając równanie (31) możemy wyznaczyć moment bezwładności tarczy względem
pionowej osi obrotu przechodzącej przez jej środek masy:

(32)

Umieszczając na tarczy badany obiekt w taki sposób by środek masy członu znajdował się na
osi obrotu tarczy z członem uzyskujemy równanie w postaci:

(33)

gdzie: m

C

– masa członu manipulatora, B

C

– moment bezwładności członu względem osi

obrotu tarczy.

Przekształcając (33) analogicznie jak równanie (29) mamy:

(34)

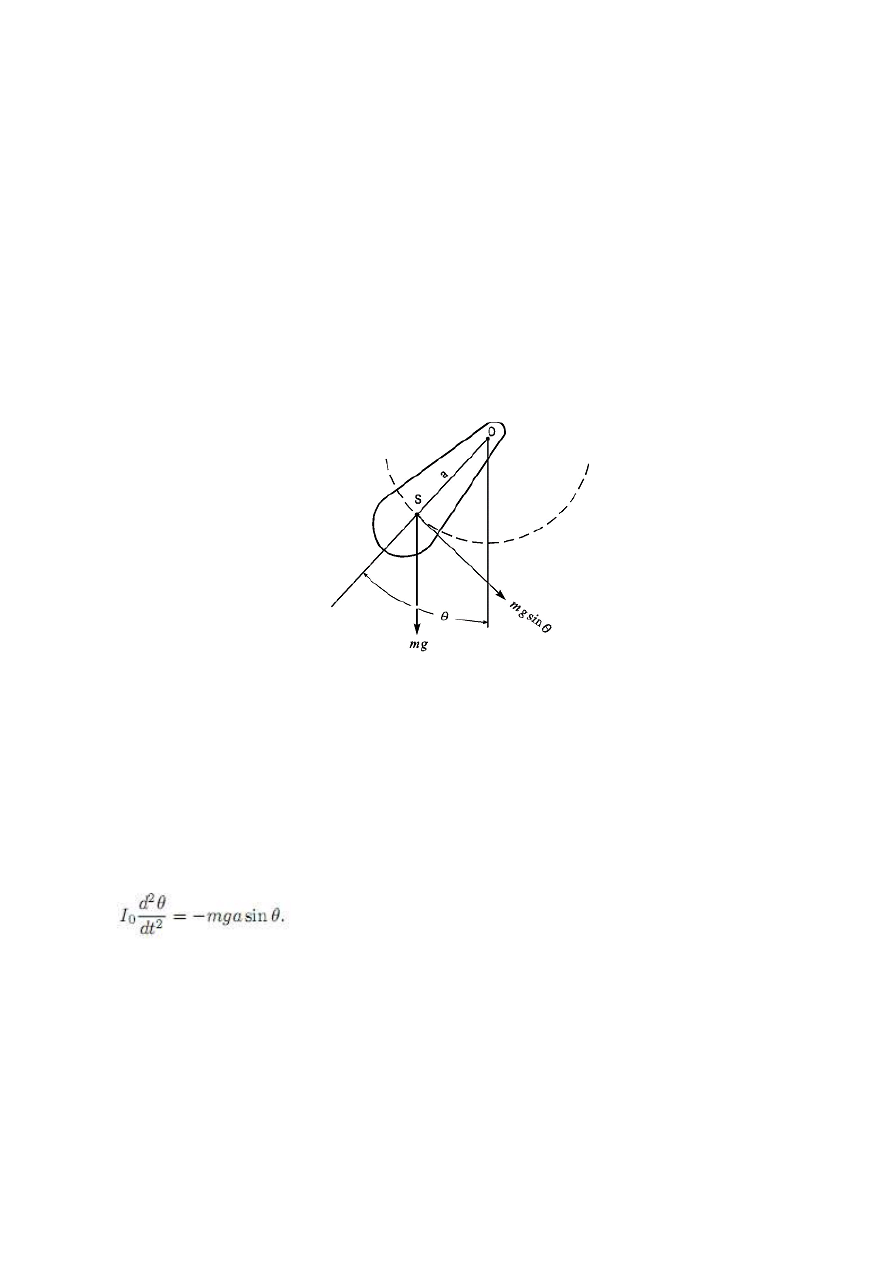
gdzie: T

C

– okres drgań skrętnych układu tarcza – badany obiekt.

Metoda z wykorzystaniem wahadła fizycznego

Wahadło matematyczne

Wahadłem matematycznym nazywamy punktową masę zawieszoną na nieważkiej nici.

Wahadło fizyczne

Wahadłem fizycznym nazywamy natomiast bryłę sztywną mogącą obracać się wokół osi
obrotu O nie przechodzącej przez środek ciężkości S.

Rys.7 Wahadło fizyczne

Wahadło odchylone od pionu o kąt θ, a następnie puszczone swobodnie, będzie wykonywać
drgania zwane ruchem wahadłowym. W ruchu tym mamy do czynienia z obrotem bryły
sztywnej wokół osi O, opisuje go zatem druga zasada dynamiki dla ruchu obrotowego.

Dla wahadła fizycznego moment siły powstaje pod wpływem siły ciężkości. Dla wychylenia
θ jest równy M = mga sinθ, gdzie a oznacza odległość środka ciężkości S od osi obrotu O.
Zatem równanie ruchu wahadła można zapisać jako:

(35)

Znak minus po prawej stronie uwzględnia fakt, że moment siły jest skierowany przeciwnie do
kierunku wychylenia.

Jeżeli ograniczyć ruch do małych kątów wychylenia (kilka stopni), to sinus kąta można
zastąpić samym kątem w mierze łukowej, czyli sin θ ≈ θ. Przy tym założeniu równanie (35)
przyjmuje postać:

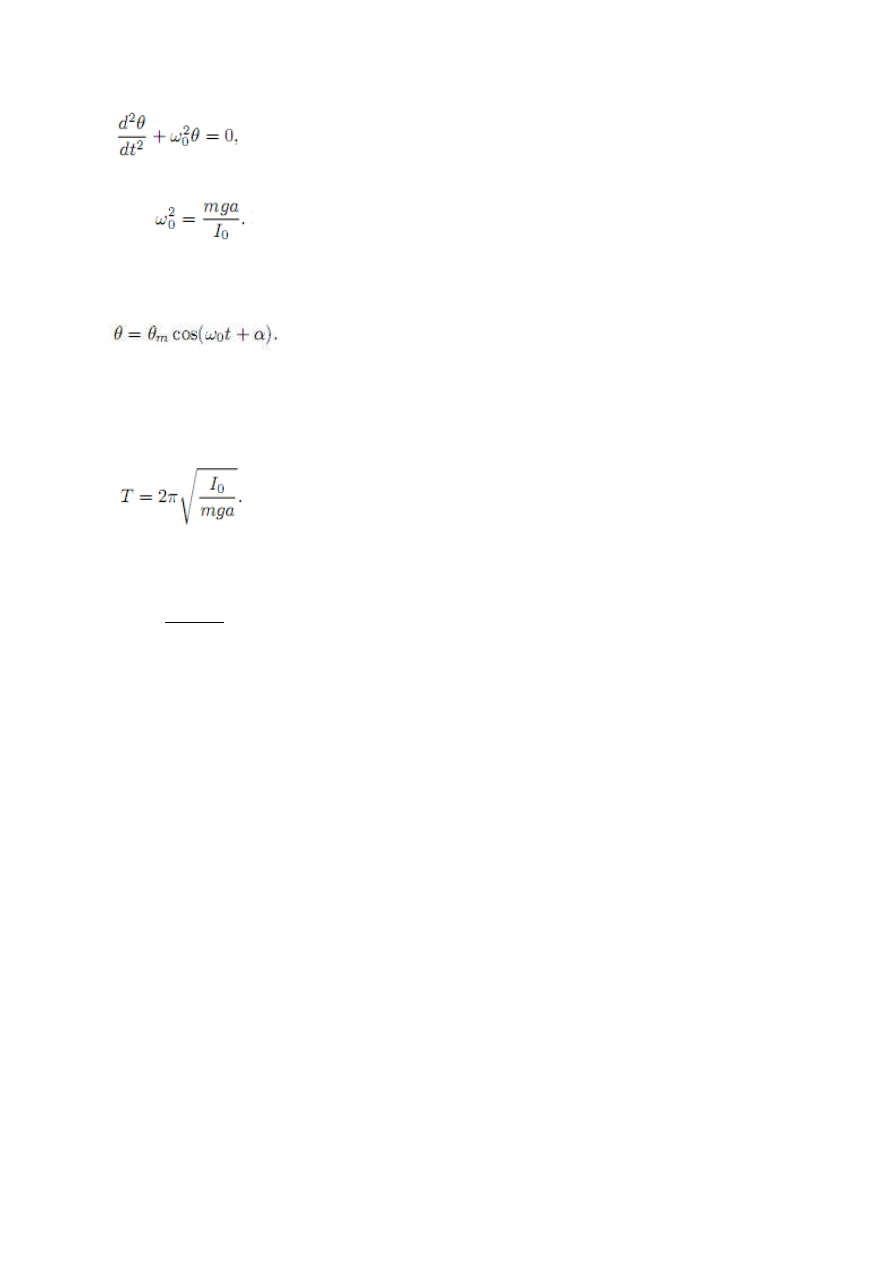
(36)

gdzie

(37)

Rozwiązaniem tego równania różniczkowego jest funkcja:

(38)

Wzór (38) wskazuje, że wahadło porusza się ruchem harmonicznym prostym. Amplituda θ

m

i

faza α zależą od warunków początkowych. Okres drgań T, związany bezpośrednio z
częstością ω

0

wynosi:

(39)

Przekształcając równanie otrzymujemy:

ࡵ

૙

ൌ

࢓ࢍࢇࢀ

૛

૝࣊

૛

(40)

2.

Przebieg laboratorium

1.

Doświadczalne wyznaczenie masowego momentu bezwładności badanych obiektów
za pomocą metody z wykorzystaniem wahadła fizycznego

2.

Analityczne wyznaczenie momentu bezwładności badanych obiektów

3.

Porównanie wyników

3.

Literatura

1.

Wyznaczanie momentu bezwładności bryły metodą wahadła fizycznego, Szkoła Główna
Gospodarstwa Wiejskiego w Warszawie, http://kf.sggw.pl/cwiczenia/O_EX08.pdf;

2.

Wahadła fizyczne, M. Nowina-Konopka, A. Zięba, Akademia Górniczo-Hutnicza w
Krakowie, www.ftj.agh.edu.pl/zdf/zeszyt/3_01n.pdf;

3.

Doświadczalne

wyznaczanie

masowych

momentów

bezwładności

części

maszyn,

Ł.Frąckowiak-Iwanicka, T.Kleikel, Uniwersytet Zielonogórski, http://www.uz.zgora.pl/
~tklekiel/tmm/cw_4.pdf;

4.

Wyznaczanie współrzędnych tensorów bezwładności członów manipulatorów, P. Szumiński,
Politechnika Łódzka, http://www.kdm.p.lodz.pl/wyklady/tmm/TMM-1.pdf;

5.

Mechanika ogólna w zarysie. Momenty bezwładności., W. Sałata, Politechnika Poznańska,
http://neur.am.put.poznan.pl/salata/momenty_bezwladnosci.pdf;

6.

Dynamika bryły sztywnej, L.J. Maksymowicz, Akademia Górniczo-Hutnicza w Krakowie,
home.agh.edu.pl/~limaksy/wyklady/brylasz.doc.