
Metody Matematyczne w Elektrotechnice
®
1
Zmienne stanu
Prowadzący: dr inż. Tomasz Sikorski
Instytut Podstaw Elektrotechniki i Elektrotechnologii
Wydział Elektryczny
Politechnika Wrocławska
D-1, 205/8
tel: (071) 320 21 60
fax: (071) 320 20 06
email:
Metody Matematyczne w Elektrotechnice
1. Wprowadzenie ............................................................................................................................................................................................................... 3
2. Przykład opisu układu za pomocą zmiennych stanu...................................................................................................................................................... 7
Wykorzystanie wartości własnych macierzy stanu
do badania stabilności układu....................................................................................... 23
®
2

Metody Matematyczne w Elektrotechnice
1. Wprowadzenie
Stanem obwodu w chwili t
0
nazywamy zespół wielkości, które razem ze znajomością wszystkich sygnałów
wejściowych (tj. źródeł napięcia i źródeł prądu), pozwalają przewidzieć jednoznacznie zachowanie się
układu w każdej chwili t>t
0
tzn. pozwalają na jednoznaczne określenie wszystkich sygnałów wyjściowych
(napięć i prądów) wszystkich elementów obwodu.
Zmiennymi stanu nazywamy taki układ wielkości, który jednoznacznie opisuje stan obwodu. Wielkości te
nazywane są zmiennymi stanu lub współrzędnymi stanu, a wektor będący zbiorem n zmiennych stanu
nazywamy wektorem stanu.
W obwodach elektrycznych stan obwodu jednoznacznie opisują ładunku na kondensatorach, a zatem
również napięcia na kondensatorach, oraz strumienie cewek czyli również prądy płynące przez cewki.
Wielkości te przyjmiemy za zmienne stanu.
Dla obwodów nie zawierających oczek osobliwych oraz węzłów (rozcięć) osobliwych liczba zmiennych
stanu jest równa liczbie elementów zachowawczych tj. liczbie kondensatorów i cewek. W ogólności o ilości
zmiennych stanu świadczy rząd obwodu (liczba stopni swobody)
LC
L
C
n
n
n
n
=
−
−
gdzie
LC
n
– całkowita liczba kondensatorów i cewek,
L
n
- liczba niezależnych węzłów osobliwych,
-
liczba niezależnych oczek osobliwych.
C
n
Dla n zmiennych stanu możemy sformułować n równań różniczkowych pierwszego rzędu lub jedno
równanie n-tego rzędu. To drugie podejście jest podstawą metody klasycznej rozwiązywania obwodów w
®
3

Metody Matematyczne w Elektrotechnice
stanach przejściowych, dające rozwiązanie dla jednej zmiennej, będącej podstawą rozwiązywanego
równania n-tego rzędu. W metodzie zmiennych stanu wykorzystamy układ n równań pierwszego
stopnia.
Oznaczmy zmienne stanu za pomocą
( ) ( ) ( )
( )
1
2
3
n
x t ,x t ,x t ...x t
, a odpowiadający im kolumnowy
wektor zmiennych stanu o wymiarach nx1 jako:
( )
( )
( )
( )
1
2
...
n
x t
x t
t
x t
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
nx1
⎢
⎥
⎣
⎦
X
Oznaczmy wymuszenia tj. niesterowane źródła napięciowe i prądowe przez
( ) ( ) ( )
( )
1
2
3
n
u t ,u t ,u t ...u t
, a
odpowiadający im kolumnowy wektor wymuszeń o wymiarach px1 jako:
( )
( )
( )
( )
1
2
...
p
u t
u t
t
u
t
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
U
px1
⎢
⎥
⎢
⎥
⎣
⎦
®
4
Metody Matematyczne w Elektrotechnice
Pisząc układ równań Kirchhoffa dla danego obwodu możemy tak przekształcić zależności z równaniami
pierwszego rzędu by otrzymać formę, gdzie z lewej strony występują pierwsze pochodne zmiennych stanu,
a z drugiej zmienne stanu i wymuszenia. Jest to tzw. postać normalna równania stanu.
( )
( )
( )
d
t
t
t
dt
=
+
X
AX
BU
bądź
( )
( )
( )
' t
t
t
=
+
X
AX
BU
Macierze
A
i w obwodzie liniowym mają elementy stałe, liczbowe, stanowiące kombinacje
elementów obwodu.
B
Przy czym:
A
jest macierzą kwadratową o wymiarach nxn i zwana jest macierzą stanu,
B
jest macierzą prostokątną o wymiarach nxp i zwana jest macierzą wymuszeń.
Pełen opis obwodu, zawierający informacje o napięcia na cewkach, rezystorach czy prądach płynących
przez kondensatory, można sformułować drugim równaniem, opartym na zmiennych stanu. Równanie to
jest równaniem algebraicznym i nazywane jest równaniem odpowiedzi.
( )
( )
( )
t
t
t
=
+
Y
CX
DU
gdzie
( )
( )
( )
( )
1
2
...
q
y t
y t
t
y t
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Y
qx1 – wektor odpowiedzi
Przy czym: jest macierzą prostokątną o wymiarach qxn i zwana jest macierzą odpowiedzi,
C
D
jest macierzą prostokątną o wymiarach qxp i zwana jest macierzą transmisyjną.
®
5

Metody Matematyczne w Elektrotechnice
®
6
Równanie stanu i równanie odpowiedzi tworzą parę równań, które w pełni opisują stan obwodu w
warunkach dynamicznych.
Charakterystyczną cechą metody zmiennych stanu jest możliwość jednoczesnego wyznaczania
zmienności w czasie wszystkich wielkości uznanych za zmienne stanu. Ponadto metoda ta umożliwia
analizę obwodów różnej klasy, tj. liniowych i nieliniowych oraz stacjonarnych i niestacjonarnych. I wreszcie
oparcie równań tylko na pierwszej pochodnej, a także specjalna struktura równań wektorowo-macierzowa,
stwarza dobre warunki do aplikacji metody zmiennych stanu przy użyciu komputerów.
Metody Matematyczne w Elektrotechnice
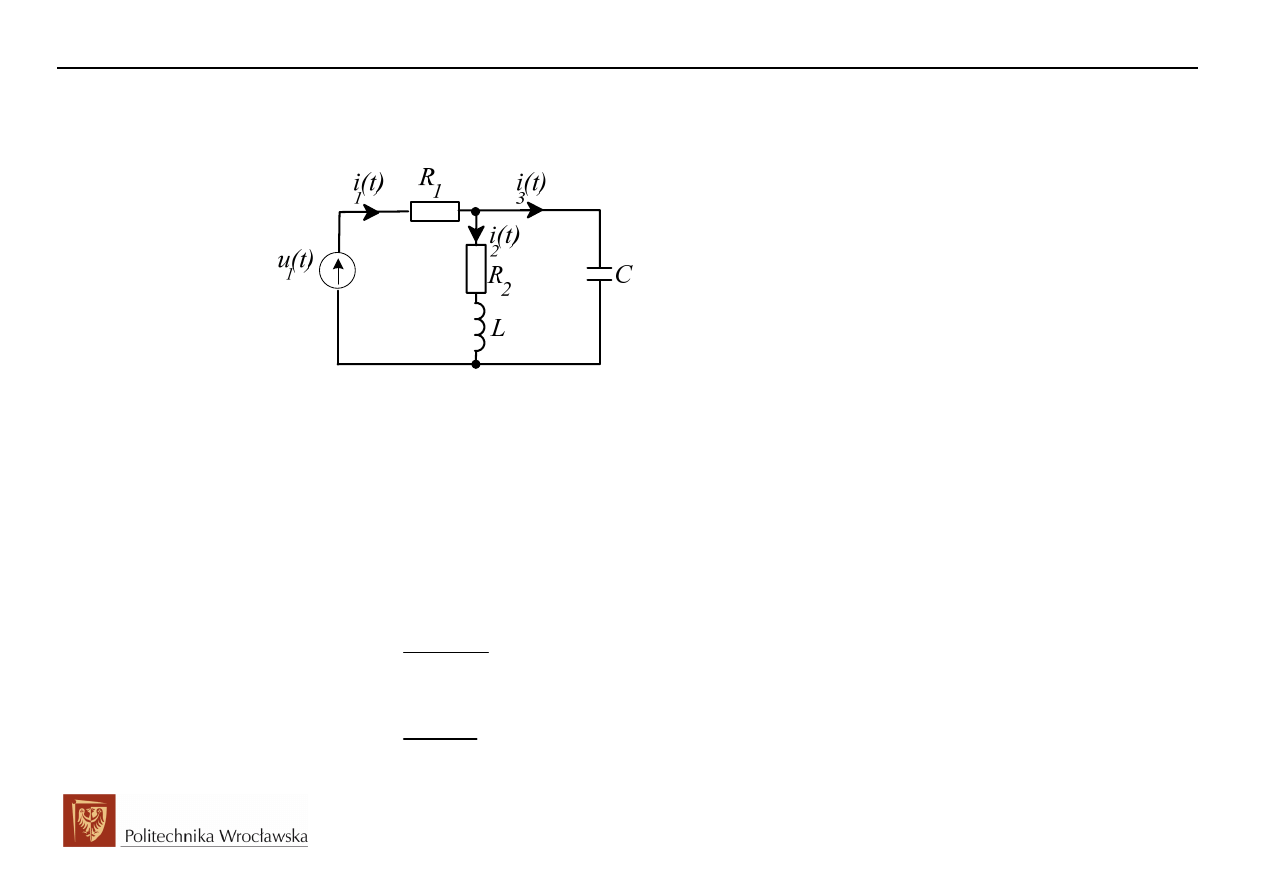
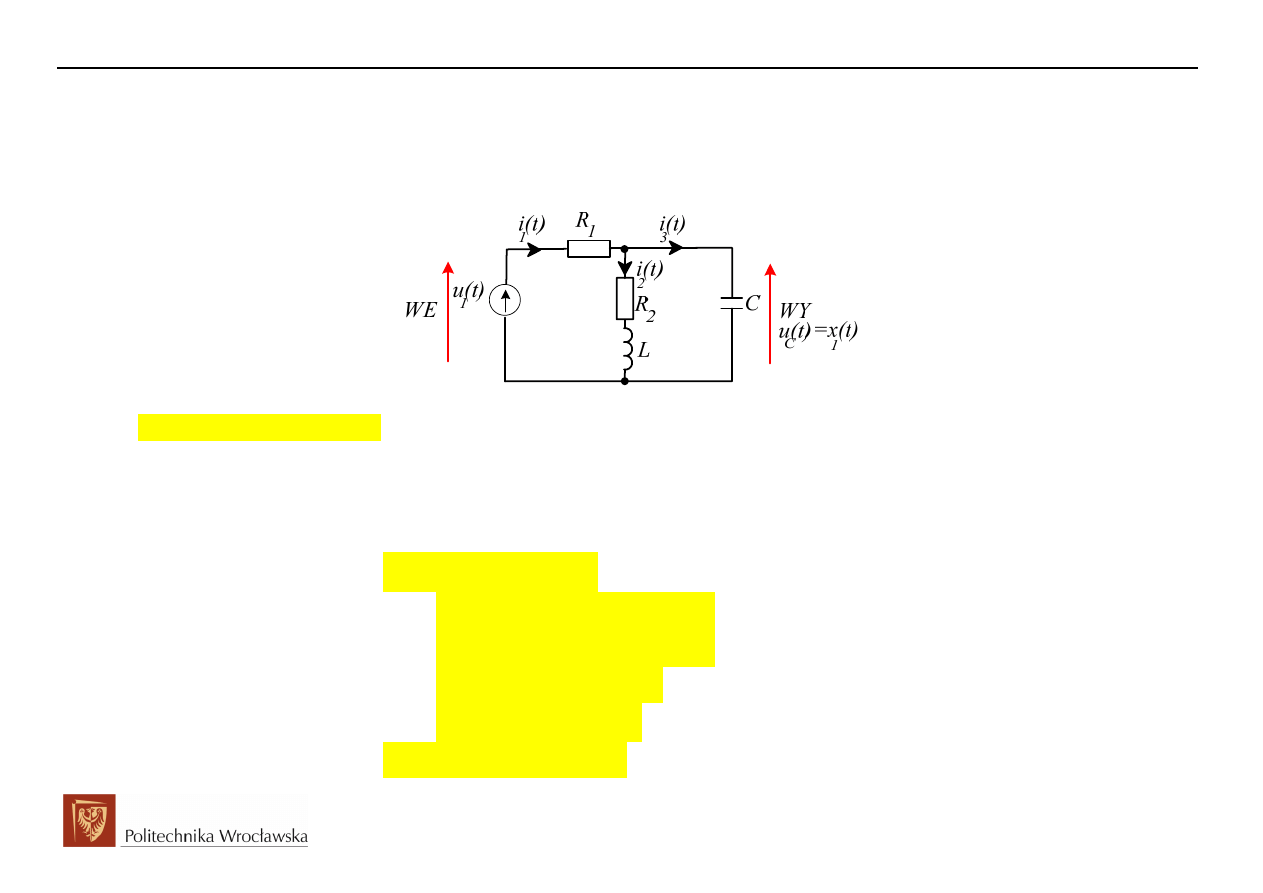
2. Przykład opisu układu za pomocą zmiennych stanu
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
2.1 Formułowanie równania stanu
Formułowanie równania zmiennych stanu oraz równania odpowiedzi pokażemy na przykładzie.
Stwierdzamy brak oczek oraz węzłów osobliwych, a więc rząd obwodu równy jest liczbie elementów
zachowawczych, n=2, i tyleż samo wyznaczymy zmiennych stanu.
Spodziewamy się:
( )
( )
( )
1
2
x t
t
x t
⎡
⎤
= ⎢
⎥ nx1=2x1;
⎣
⎦
X
A
nxn=2x2;
( )
( )
1
t
u t
= ⎡
⎤
⎣
⎦
U
px1=1x1; nxp=2x1
B
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
3
1
2
2
2
2
C
'
C
'
L
du
t
x t
u
t
i t
C
C x
t
dt
di t
x t
i t
u
t
L
L x
t
dt
=
⎯⎯
→
=
= ⋅
=
⎯⎯
→
=
= ⋅
®
7
Metody Matematyczne w Elektrotechnice
Punktem wyjścia do wyznaczenia równania stanu jest układ równań Kirchhoffa:
( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
2
1
1 1
2 2
2
2 2
C
i t
i t
i t
di t
u t
R i t
R i t
L
dt
di t
R i t
L
u
t
dt
⎧
=
+
⎪
⎪
⎪
=
+
+
⎨
⎪
⎪
+
=
⎪⎩
;
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
1
2
1
'
1
1 1
2
2 2
'
2
2 2
1
1
2
i t
x t
Cx
t
u t
R i t
Lx t
R x t
Lx t
R x t
x t
⎧
=
+
⎯⎯
→
⎪⎪
=
+
+
⎨
⎪
+
=
⎪⎩
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
'
1
1 2
1
1
2
2 2
'
'
2
2
2 2
1
2
1
2
1
u t
R x t
R Cx
t
Lx t
R x t
R
Lx t
R x t
x t
x t
x t
x t
L
L
⎧
=
+
+
+
⎪
⎨
+
=
⎯⎯
→
=
−
⎪⎩
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
2
1
1 2
1
1
1
2
2 2
'
2
2
1
2
1
1
R
u t
R x t
R Cx t
L
x t
x t
R x t
L
L
R
x t
x t
x t
L
L
⎧
⎛
⎞
=
+
+
−
+
⎜
⎟
⎪⎪
⎝
⎠
⎨
⎪⎯⎯→
=
−
⎪⎩
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 2
2 2
2 2
'
1
1
1
1
'
2
2
1
2
1
R x t
R x t
R x t
u t
R Cx t
x t
R
x t
x t
x t
L
L
−
⎧
=
+
+
+
⎪
⎨
⎯⎯
→
=
−
⎪⎩
®
8

Metody Matematyczne w Elektrotechnice
( )
( )
( )
( )
( )
( )
( )
'
1
1
1
1 2
1
'
2
2
1
2
1
R Cx t
x t
R x t
u t
R
x t
x t
x t
L
L
⎧
= −
−
+
⎪
⎨
⎯⎯
→
=
−
⎪⎩
( )
( )
( )
( )
( )
( )
( )
'
1
1
2
1
1
1
'
2
2
1
2
1
1
1
1
x t
x t
x t
u t
R C
C
R C
R
x t
x t
x t
L
L
⎧⎯⎯→
= −
−
+
⎪⎪
⎨
⎪⎯⎯→
=
−
⎪⎩
®
9
Metody Matematyczne w Elektrotechnice
Postać normalna równania stanu w postaci wektorowo macierzowej:
( )
( )
( )
( )
( )
'
1
1
1
1
1
'
2
2
2
1
1
1
1
0
x t
x t
R C
C
R C
u t
x t
x t
R
L
L
⎡
⎤
−
−
⎡
⎤
⎢
⎥
⎡
⎤
⎡
⎤ ⎢
⎥
⎢
⎥
=
+
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥ ⎣
⎦
⎣
⎦
⎢
⎥
−
⎣
⎦
⎢
⎥
⎣
⎦
( )
( )
( )
1
2
x t
t
x t
⎡
⎤
= ⎢
⎥ nx1=2x1;
wektor zmiennych stanu
⎣
⎦
X
1
2
1
1
1
R C
C
R
L
L
⎡
⎤
−
−
⎢
⎥
⎢
⎥ nxn=2x2;
macierz stanu;
dla danych
=
⎢
⎥
−
⎢
⎥
⎣
⎦
A
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
⎡
⎤
= ⎢
⎥
−
⎣
⎦
A
( )
( )
1
t
u t
= ⎡
⎤⎦
⎣
U
px1=1x1;
wektor wymuszeń
1
1
0
R C
⎡
⎤
⎢
⎥
= ⎢
⎥
nxp=2x1
macierz wymuszeń; dla
danych
⎢
⎥
⎣
⎦
B
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
B
®
10

Metody Matematyczne w Elektrotechnice
2.2 Elementy rozwiązania równania stanu
Jeśli rozpatrywać dynamikę pracy obwodu elektrycznego tj. wykorzystać równanie stanu do analizy
obwodu w stanie nieustalonym, konieczna jest znajomość stanu początkowego w chwili komutacji t=t
0
.
Określa to wektor stanu początkowego, tj. wektor stanu dla t=t
0
.
( )
( )
( )
1
0
2
0
0
0
...
n
x t
x t
x t
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
nx1
⎢
⎥
⎣
⎦
X
Rozwiązanie równania stanu
( )
( )
( )
' t
t
t
=
+
X
AX
BU
w ogólnym zapisie ma postać:
( )
(
)
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
τ
τ τ
−
−
=
+
∫
A
A
X
X
BU
Natomiast wektor odpowiedzi
( )
( )
( )
t
t
t
Y
=
+
CX
DU
, w ogólnym zapisie reprezentuje równanie:
( )
(
)
( )
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
t
τ
τ τ
−
−
=
+
+
∫
A
A
Y
C
X
C
BU
DU
fragment
(
)
( )
0
0
t t
e
t
−
A
X
zależy od wektora stanu początkowego, występuje tylko przy stanie
początkowy niezerowym,
®
11
Metody Matematyczne w Elektrotechnice
fragment
( )
( )
0
t
t
t
e
d
τ
τ τ
−
∫
A
BU
, bądź
( )
( )
0
t
t
t
e
d
τ
τ τ
−
∫
A
C
BU
jest splotem dwóch funkcji macierzowych i
reprezentuje działanie wymuszeń.
Charakterystycznym elementem obu równań jest macierz
( )
t
e
A
zwana macierzą podstawową lub
tranzycyjną układu. Kluczowe znaczenie dla rozwiązania równania stanu będzie miała umiejętność
wyznaczenia macierzy podstawowej.
Pewnym kierunkiem jest wykorzystanie metody rozwinięcia w szereg skończony
( )
t
e
A
ze względu na
kwadratową macierz
A
przy danym rzędzie obwodu n.
( )
( )
( )
1
0
n
t
k
k
k
g
e
t
β
−
=
=
=
∑
A
A
A
Rozwinięcie to wykorzystuje twierdzenie twierdzenie Cayleya-Hamiltona, które mówi, iż każda macierz
kwadratowa spełnia swoje równanie charakterystyczne, co oznacza:
( )
( )
0
0
g
g
λ
= ⎯⎯
→
=
A
dla pierwiastków równania charakterystycznego.
Dla rozpatrywanego przykładu n=2, stąd rozwinięcie przyjmie postać:
( )
( )
( )
( )
1
0
1
1
t
g
e
t
t
β
β
=
=
+
A
A
A
gdzie 1 oznacza diagonalną macierz jednostkową nxn.
®
12

Metody Matematyczne w Elektrotechnice
Macierz stanu, po podstawieniu danych, wynosi
1
1
1
1
−
−
⎡
⎤
= ⎢
⎥
−
⎣
⎦
A
, co pozwala przedstawić rozwinięcie
macierzy podstawowej w zapisie wektorowo-macierzowym:
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1 0
1
1
0
0 1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
⎡
⎤ ⎡
⎤
−
−
−
−
⎡
⎤
⎡
⎤
=
=
+
=
+
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
−
⎣
⎦
⎣
⎦ ⎣
⎦ ⎣
A
A
⎦
Do wyznaczenie współczynników rozkładu
( ) ( )
0
1
,
t
t
β
β
wykorzystamy pojęcie
równania
charakterystycznego macierzy stanu
A
(kwadratowej) i wywodzących się z tego równania wartości
własne macierzy stanu.
Mając daną macierz kwadratową
A
możemy wyznaczyć wielomian charakterystyczny tej macierzy jako:
( )
[
]
det
1
g
λ
λ
=
−
A
gdzie 1 oznacza diagonalną macierz jednostkową nxn.
Następnie równanie:
( )
[
]
0
det
1
0
g
λ
λ
= ⎯⎯
→
−
=
A
jest równaniem charakterystycznym macierzy
A
, a wywodzące się z tego równania pierwiastki
nazywamy pierwiastkami charakterystycznymi bądź wartościami własnymi macierzy kwadratowej
A
.
®
13

Metody Matematyczne w Elektrotechnice
Spróbujmy więc wyznaczyć macierz podstawową
( )
t
e
A
w następujących operacjach:
wyznaczenie równania charakterystycznego macierzy
A
wyznaczenie pierwiastków równania charakterystycznego (wartości własnych macierzy
A
)
na podstawie rozwinięcia w szereg skończony macierzy podstawowej, wykorzystać wartości własne
do wyznaczenia współczynników rozwinięcia tej macierzy w szereg
Wyznaczenie równania charakterystycznego macierzy
A
( )
[
]
(
)
(
)
1
1
1
1
1 0
1
1
0
det
1
1
1
1
1
0 1
1
1
0
g
λ
λ
λ
λ
λ
λ
λ
− −
−
−
−
−
−
⎡
⎤
⎡
⎤
⎡
⎤ ⎡
⎤
=
−
=
−
=
−
=
⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
− −
−
−
⎣
⎦
⎣
⎦
⎣
⎦ ⎣
⎦
A
( ) (
)
2
2
1
1
2
2
g
λ
λ
λ
λ
= +
+ =
+
+
Wyznaczenie pierwiastków równania charakterystycznego (wartości własnych macierzy
A
)
( )
2
2
1
2
0
2
2 0
4
4 8
4;
2
2
2
1
1
2
2
2
2
1
1
2
2
g
b
ac
j
b
j
j
b
j
j
λ
λ
λ
λ
λ
= ⎯⎯
→
+
+ =
Δ =
−
= − = −
Δ =
− + Δ
− +
=
=
= − +
− − Δ
− −
=
=
= − −
®
14

Metody Matematyczne w Elektrotechnice
Wyznacznie macierzy podstawowej przez wyznaczenia współczynników rozwinięcia tej macierzy w
szereg skończony.
Przypomnijmy postać rozwinięcia:
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1 0
1
1
0
0 1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
⎡
⎤ ⎡
⎤
−
−
−
−
⎡
⎤
⎡
⎤
=
=
+
=
+
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
−
⎣
⎦
⎣
⎦ ⎣
⎦ ⎣
A
A
⎦
Jednocześnie przy wartościach własnych macierzy (dla pierwiastków równania charakterystycznego)
( )
( )
( )
0
0
i
t
i
g
g
e
g
λ
λ
λ
= ⎯⎯
→
= ⎯⎯
→
=
A
czyli:
( )
( )
0
1
t
e
t
t
λ
β
β
λ
=
+
(dla pierwiastków równania charakterystycznego)
to przy danych pierwiastkach
( )
( )(
)
( )
( )(
)
1
2
1
0
1
2
0
1
1
1
1
1
1
1
t
1
1
t
j
e
t
t
j
®
15
j
e
t
t
j
λ
λ
β
λ
β
β
+
− +
= − − ⎯⎯
→
=
+
− −
λ
β
= − + ⎯⎯
→
=
Otrzymamy dwie informacje przy dwóch poszukiwanych współczynnikach rozwinięcia (funkcji zmiennej t):
(
)
( )
( )(
)
(
)
( )
( )(
)
1 1
0
1
1 1
0
1
1
1
1
1
j t
j t
e
t
t
j
e
t
t
j
β
β
β
β
− +
− −
⎧
=
+
− +
⎪
⎨
=
+
− −
⎪⎩

Metody Matematyczne w Elektrotechnice
Przez obustronne odjęcie stronami uzyskamy:
(
)
(
)
( )
( )(
)
( )
( )(
)
(
)
( )
(
)
( )
( )
1 1
1 1
0
1
0
1
1
1
1
1
1
1
1
2
2sin
2
sin
j t
j t
t
jt
jt
t
t
e
e
t
t
j
t
t
j
e
e
e
j
t
e
j
t
j
t
t
e
t
β
β
β
β
β
β
β
− +
− −
−
−
−
−
−
=
+
− +
−
−
− −
−
=
=
⎯⎯
→
=
Przez obustronne zsumowanie stronami uzyskamy:
(
)
(
)
( )
( )(
)
( )
( )(
)
(
)
( )
( )
(
)
( )
( )
(
)
( )
( )
1 1
1 1
0
1
0
1
0
1
0
1
0
1
1
1
1
1
2
2
2cos
2
cos
cos
sin
j t
j t
t
jt
jt
t
t
t
t
e
e
t
t
j
t
t
j
e
e
e
t
t
e
t
t
t
t
e
t
t
e
t
e
t
β
β
β
β
β
β
β
β
β
β
− +
− −
−
−
−
−
−
−
+
=
+
− +
+
+
− −
+
=
−
=
−
⎯⎯
→
=
+
=
+
Ostatecznie:
( )
1
sin
t
t
e
t
β
−
=
;
( )
(
)
0
cos
sin
t
t
e
t
t
β
−
=
+
Szukana macierz podstawowa
( )
t
e
A
względem macierzy
A
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
1
0
1
1
0
1 0
1
1
0
0 1
1
1
t
t
t
t
g
e
t
t
t
t
t
β
β
β
β
β
β
β
β
⎡
⎤ ⎡
⎤
−
−
−
−
⎡
⎤
⎡
⎤
=
=
+
=
+
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
−
⎣
⎦
⎣
⎦ ⎣
⎦ ⎣
A
A
si
n
n
t
t
t
t
t
t
t
t
t
e
t
t
e
t
e
t
g
e
e
t
t
e
e
t
e
e
t
e
t
e
t
−
−
−
−
−
−
−
−
−
⎡
⎤
+
⎡
⎤
−
−
=
=
+
⎢
⎥ ⎢
⎥
+
−
⎣
⎦
⎦
( )
( )
(
)
(
)
cos
sin
0
sin
sin
0
cos
sin
sin
si
cos
sin
co
t
t
t
t
−
=
®
16
s
⎡
⎤
−
⎢
⎥
⎣
⎦
⎣
⎦
A
A

Metody Matematyczne w Elektrotechnice
---------------------------------------------------------------------------------------------------------------------------------------------
UWAGA:
Metoda rozwinięcia w szereg skończony jest szczególnie przydatna, gdy macierz kwadratowa
A
ma
wielokrotne wartości własne. Np. niech pierwiastek
i
λ
ma krotność
2
i
m
=
.Należy wtedy dla tej wartości
własnej, oprócz równania
( )
i
t
i
e
g
λ
λ
=
,zapisać dodatkowe równanie
( )
i
i
i
t
i
d
d
e
g
dt
d
λ
λ λ
λ λ
λ
λ
=
=
=
UWAGA:
Istnieją jeszcze inne metody wyznaczania macierzy podstawowej
( )
t
e
A
:
zastosowanie wzoru interpolacyjnego Sylevestera
metoda przekształceń macierzowych z użyciem nieosobliwej macierzy przekształceń
1
−
=
D P AP
---------------------------------------------------------------------------------------------------------------------------------------------
Wracając do głównego równania możemy wyznaczyć wektor stanu:
( )
(
)
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
τ
τ τ
−
−
=
+
∫
A
A
X
X
BU
Dla przypadku t
0
=0 oraz zerowych warunków początkowych, wektor stanu określa równanie:
( )
( )
( )
0
t
t
t
e
d
τ
τ τ
−
=
∫
A
X
BU
czyli splot funkcji macierzowych.
®
17

Metody Matematyczne w Elektrotechnice
®
18
⎣
W danym zadaniu:
( )
( )
U
1
t
u t
= ⎡
⎤⎦ px1=1x1;
wektor wymuszeń
1
1
0
R C
⎡
⎤
⎢
⎥
= ⎢
⎥
nxp=2x1
macierz wymuszeń; dla
danych
⎢
⎥
⎣
⎦
B
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
B
( )
( )
(
)
(
)
(
)
(
)
( )
1
0
cos
sin
1
sin
cos
0
t
t
t
t
t
e
u
d
t
t
τ
τ
τ
τ
τ
τ
τ
− −
⎡
⎤
−
−
−
−
⎡ ⎤
⎡
⎤
=
⋅
⋅
⎢
⎥ ⎢ ⎥ ⎣
⎦
−
−
⎣ ⎦
⎣
⎦
∫
X
Bądź ze względu na przemienność splotu
( )
( )
(
)
(
)
1
0
0
cos
sin
1
sin
cos
0
t
t
t
t
t
t
t
e
t
d
e
u t
d
t
t
τ τ
τ
τ
−
⎡
⎤ ⎡ ⎤
⎡
⎤
=
−
=
⋅
−
⎢
⎥ ⎢ ⎥ ⎣
⎦
⎣
⎦ ⎣ ⎦
∫
∫
A
X
BU
( )
(
)
(
)
(
)
1
0
1
0
1
0
cos
cos
sin
sin
t
t
t
t
t
t
e
t
u t
d
t
t
e
u t
d
t
e
t
u t
d
τ
τ
τ
τ
τ
τ
−
−
−
⎡
⎤
⎡
⎤
⋅
−
⎢
⎥
⎣
⎦
⎡
⎤
⎢
⎥
⎡
⎤
=
⋅
−
=
⎢
⎥ ⎣
⎦
⎢
⎥
⎣
⎦
⎢
⎥
⎡
⎤
⋅
−
⎣
⎦
⎢
⎥
⎣
⎦
∫
∫
∫
X
UWAGA:
Wyznaczanie zmiennych stanu jest efektywniejsze przy wykorzystaniu transformaty Laplace’a w
połączeniu z metoda przekształceń macierzowych.

Metody Matematyczne w Elektrotechnice
2.3 Wykorzystanie transformaty Laplace’a w wyznaczaniu zmiennych stanu
Powróćmy do postaci normalna równania stanu.
( )
( )
( )
d
t
t
t
dt
=
+
X
AX
BU
bądź
( )
( )
( )
' t
t
t
=
+
X
AX
BU
i dokonajmy obustronnie transformacji Laplace’a:
( )
( )
( )
( )
( )
( )
( )
( )
(
) ( )
( )
( )
( ) (
)
( )
( )
( )
0
0
0
1
0
1
s
s
1
1
s
t
s
s
s
s
s
t
s
s
s
t
s
s
s
t
s
−
−
−
=
+
⎯⎯
→
−
=
+
⎯⎯
→
−
=
+
⎯⎯
→
=
−
+
⎡
⎤
⎣
⎦
⎯⎯
→
=
X
X
AX
BU
X
AX
BU
X
A X
BU
X
X
A
BU
X
X
P R
Niech
, a
(
)
1
s
=
−
P
A
( )
( )
0
s
t
=
+
R BU
X
W omawianym przykładzie
( )
( )
( )
( )
( )
'
1
1
1
1
1
'
2
2
2
1
1
1
1
0
x t
x t
R C
C
R C
u t
x t
x t
R
L
L
⎡
⎤
−
−
⎡
⎤
⎢
⎥
⎡
⎤
⎡
⎤ ⎢
⎥
⎢
⎥
=
+
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥ ⎣
⎦
⎣
⎦
⎢
⎥
−
⎣
⎦
⎢
⎥
⎣
⎦
®
19

Metody Matematyczne w Elektrotechnice
( )
( )
( )
1
2
x t
t
x t
⎡
⎤
= ⎢
⎥ nx1=2x1;
wektor zmiennych stanu
⎣
⎦
X
1
2
1
1
1
R C
C
R
L
L
⎡
⎤
−
−
⎢
⎥
⎢
⎥ nxn=2x2;
macierz stanu;
dla danych
=
⎢
⎥
−
⎢
⎥
⎣
⎦
A
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
⎡
⎤
= ⎢
⎥
−
⎣
⎦
A
( )
( )
1
t
u t
= ⎡
⎤⎦
⎣
U
px1=1x1;
wektor wymuszeń
1
1
0
R C
⎡
⎤
⎢
⎥
= ⎢
⎥
nxp=2x1
macierz wymuszeń; dla
danych
⎢
⎥
⎣
⎦
B
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
B
Po podstawieniu danych:
( )
( )
( )
( )
( )
'
1
1
1
'
2
2
1
1
1
1
1
0
x t
x t
u t
x t
x t
⎡
⎤
⎡
⎤
−
−
⎡
⎤
⎡ ⎤
=
+
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢ ⎥ ⎣
⎦
−
⎣
⎦
⎣ ⎦
⎣
⎦
⎣
⎦
®
20

Metody Matematyczne w Elektrotechnice
Po przejściu do dziedziny operatorowej
( ) (
)
( )
( )
( )
( )
( )
( )
( )
( )
0
1
1
0
0
0
1
0
1
1
1 0
1
1
1
1
1
0 1
1
1
1
1
1
0
0
t
s
s
s
t
s
s
s
s
U s
s
t
s
U s
−
−
⎡ ⎤
=⎢ ⎥
⎣ ⎦
=
−
+
=
⎡
⎤
⎣
⎦
−
−
+
⎡
⎤ ⎡
⎤ ⎡
⎤
⎯⎯
→ = − =
−
=
⎢
⎥ ⎢
⎥ ⎢
⎥
−
−
+
⎣
⎦ ⎣
⎦ ⎣
⎦
⎡
⎤
⎡ ⎤
⎯⎯
→ =
+
⎯⎯⎯⎯→ =
=
⋅
=
⎡
⎤ ⎢
⎥
⎢ ⎥ ⎣
⎦
⎣ ⎦
⎣
⎦
X
X
A
BU
X
P R
P
A
R BU
X
R BU
Dalej:
1
1
det
T
−
=
⋅
P
P
D
P
gdzie:
( )
( )
( )
( )
( )
( )
(
)(
) ( )( )
1 1
1 2
22
21
2 1
2 2
12
11
2
11 22
12
21
1
1
1
1
1
1
1
1
1
1
1
1
det
1
1
1
1
2
2
transpose
T
p
p
s
s
s
s
p
p
p p
p p
s
s
s
s
+
+
+
+
⎡
⎤
−
−
⎡ +
− − ⎤
+
−
⎡
⎤
⎢
⎥
=
=
⎯⎯⎯⎯
→
=
⎢
⎥
⎢
⎥
−
+
+
⎢
⎥
−
−
⎣
⎦
⎣
⎦
⎣
⎦
=
−
= +
+ −
− =
+
+
P
P
D
D
P
Stąd:
1
2
1
1
1
1
1
1
det
2
2
T
s
s
s
s
−
+
−
⎡
⎤
=
⋅
=
⎢
⎥
+
+
+ ⎣
⎦
P
P
D
P
( )
( )
( )
1
1
1
0
0
U s
s
U s
⎡
⎤
⎡ ⎤
=
=
⋅
=
⎡
⎤ ⎢
⎥
⎢ ⎥ ⎣
⎦
⎣ ⎦
⎣
⎦
R BU
Wektor transformat Laplaca zmiennych stanu dla danego przykładu:
( )
( )
1
1
2
1
1
1
1
1
2
2
0
s
U s
s
s
s
s
−
+
−
⎡
⎤
⎡
⎤
=
=
⋅ ⎢
⎥
⎢
⎥
+
+
+ ⎣
⎦ ⎣
⎦
X
P R
®
21
Metody Matematyczne w Elektrotechnice
Jeśli wymuszeniem będzie np. napięcie stałe E=1V to
( )
1
1
U s
s
=
Wtedy:
( )
(
)
(
)
2
1
2
2
2
1
1
2
2
1
1
1/
1
1
1
1
0
1
1
2
2
2
2
2
2
s
s
s s
s
s
s
s
s
s
s
s
s
s
s
s s
s
−
+
⎡
⎤
+
⎡
⎤ ⎢
⎥
+
+
⎢
⎥
+
−
⎡
⎤ ⎡
⎤
⎢
⎥
=
=
⋅
=
=
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
+
+
+
+
+
⎣
⎦ ⎣
⎦
⎢
⎥ ⎢
⎥
⎢
⎥
⎣
⎦
+
+
⎢
⎥
⎣
⎦
X
P R
Poszukiwane zmienne stanu:
( )
( )
{
}
( )
( )
(
)
(
)
1
2
1
1
2
1
2
1
2
2
1
2
2
s
s s
s
x t
t
s
x t
s s
s
−
−
−
⎡
⎤
⎧
⎫
+
⎪
⎪
⎢
⎥
⎨
⎬
+
+
⎢
⎥
⎪
⎪
⎡
⎤
⎩
⎭
⎢
⎥
=
= ⎢
⎥
⎢
⎧
⎫⎥
⎣
⎦
⎪
⎪
⎢
⎥
⎨
⎬
+
+
⎢
⎥
⎪
⎪
⎩
⎭
⎣
⎦
L
L
L
X
X
Rozwiązanie:
( )
( )
( )
1
1 1
1
cos
sin 1
2 2
2
t
t
C
x t
u
t
e
t
e
t
t
−
−
⎛
⎞
=
=
−
+
⎜
⎟
⎝
⎠
( )
( )
( )
2
1 1
1
cos
sin 1
2 2
2
t
t
L
x t
i
t
e
t
e
t
t
−
−
⎛
⎞
=
=
−
−
⎜
⎟
⎝
⎠
®
22

Metody Matematyczne w Elektrotechnice
2.4 Wykorzystanie wartości własnych macierzy stanu do badania stabilności układu
Możemy stwierdzić czy system jest stabilny bez wyznaczania zmiennych stanu i badani ich przebiegu.
Otóż o stabilności układu możemy wnioskować na podstawie położenia wartości własnych macierzy stanu
A
tj. pierwiastków równania charakterystycznego.
Układ jest stabilny, jeśli wszystkie wartości własne macierzy stanu mają części rzeczywiste
mniejsze od zera
{ }
Re
0
i
λ
<
W omawianym przypadku
{ }
{ }
1
1
2
2
1
1
Re
1 0
1
1
Re
1 0
j
j
λ
λ
λ
λ
= − + ⎯⎯
→
= − <
− − ⎯⎯
→
= − <
świadczy o stabilności układu.
=
®
23
Metody Matematyczne w Elektrotechnice
2.5 Wykorzystanie macierzy stanu do wyznaczania odpowiedzi impulsowej układu
Rozważmy w omawianym przykładzie jedno wejście i jedno wyjście.
Wtedy równanie odpowiedzi
®
24
( )
( )
( )
t
t
t
=
+
CX
DU
bądź:
( )
(
)
( )
( )
( )
( )
0
0
0
t
t t
t
t
t
e
t
e
d
t
τ
τ τ
−
−
=
+
+
∫
A
A
Y
C
X
C
BU
DU
Y
zawierać będzie elementy:
( )
( )
Y
1
t
y t
= ⎡
⎤⎦ qx1=1x1;
wektor odpowiedzi
⎣
( )
( )
( )
1
2
x t
t
x t
⎡
⎤
= ⎢
⎥ nx1=2x1;
wektor zmiennych stanu
⎣
⎦
X
[
]
11
12
c
c
=
C
qxn=1x2; macierz odpowiedzi
dla przypadku 1WYJ
[
] [
]
11
12
1 0
c
c
=
=
C
( )
( )
1
t
u t
= ⎡
⎤⎦
⎣
U
px1=1x1;
wektor wymuszeń
[ ]
11
d
=
D
qxp=1x1
macierz transmisyjna

Metody Matematyczne w Elektrotechnice
Z wcześniejszy wyprowadzeń:
1
2
1
1
1
R C
C
R
L
L
⎡
⎤
−
−
⎢
⎥
⎢
⎥ nxn=2x2;
macierz stanu;
dla danych
=
⎢
⎥
−
⎢
⎥
⎣
⎦
A
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
1
1
1
−
−
⎡
⎤
= ⎢
⎥
−
⎣
⎦
A
1
1
0
R C
⎡
⎤
⎢
⎥
= ⎢
⎥ nxp=2x1
macierz wymuszeń; dla
danych
⎢
⎥
⎣
⎦
B
1
2
1
1
1
R
R
;
L
H ,
C
F
Ω
=
=
=
=
1
0
⎡ ⎤
= ⎢ ⎥
⎣ ⎦
B
cos
sin
sin
cos
t
t
t
t
e
t
e
t
e
t
t
e
−
−
−
−
⎡
⎤
−
⎢
⎣
⎦
( )
t
e
=
A
⎥
nxn=2x2;
macierz podstawowa (tranzycyjna)
Dla systemu z jednym wejściem i jednym wyjściem wielkość
( )
t
e
A
C
B
równa jest odpowiedzi impulsowej.
Dla systemu o p wejść i q wyjść wielkość
( )
t
e
A
C
B
jest macierzą o wymiarze pxq , gdzie element (i,j) tej
macierzy jest funkcją odpowiedzi impulsowej i-tego wyjścia na impuls Diraca na j-tym wejściu, przy
pozostałych sygnałach wejściowych równych zeru.
®
25

Metody Matematyczne w Elektrotechnice
®
26
( )
1 0
sin
cos
0
t
t
t
e
e
t
e
t
h t
−
−
⎡ ⎤
⎤
=
−
⋅
=
=
⎢ ⎥
⎦ ⎣ ⎦
W badanym przypadku jednowejściowego i jednowyjściowego układu odpowiedź impulsowa wyniesie:
1
]
1
cos
0
cos
sin
sin
cos
t
t
t
t
t
e
t
e
t
e
e
t
t
e
t
−
−
−
−
−
⎡ ⎤ ⎡
⋅
⋅
=
⎢ ⎥ ⎣
⎣ ⎦
⎡
⎤
−
⎢
⎥
⎣
⎦
( )
[
A
C
B
Wyszukiwarka
Podobne podstrony:
Pomiary napiec zmiennych id 374 Nieznany
4IMIR prady zmienne id 39330 Nieznany (2)
AM2 11 Zamiana zmiennych id 587 Nieznany (2)
al1 w04 zima2011 id 54566 Nieznany (2)
DSaA W04 Techniques id 143853 Nieznany
MM ETK W03 zmiennestanu
Pradnica pradu zmiennego id 382 Nieznany
anl1 w04 zima2012 id 65275 Nieznany (2)
anl1 w04 lato2009 id 65274 Nieznany (2)
FUNKCJE JEDNEJ ZMIENNEJ id 1820 Nieznany
miary zmiennosci id 298408 Nieznany
M W04 57 id 274844 Nieznany
zmienne losowe dyskretne id 591 Nieznany
gs w04 id 197501 Nieznany
zmienne losowe ciagle 2 id 5914 Nieznany
Carrousel Siemiatycze MM id 108 Nieznany
6 zmienna losowa id 44007 Nieznany
więcej podobnych podstron