4.  Potêgowanie i pierwiastkowanie liczb zespolonych 

 

 

Ze wzoru na iloczyn liczb zespolonych w postaci trygonometrycznej wynika, 

¿e n

-ta 

pot

êga liczby z 

 wyra

¿a siê wzorem

 









n

sin

i

n

cos

z

z

n

n





 

znanym jako 

wzór de Moivre’a

. 

 

.......................................................................................... 

PRZYK£AD

 

Obliczy

ã 





19

2

2

i





. 

Rozwi

¹zanie

 

Przedstawimy najpierw liczb

ê 

i

2

2 



 w postaci trygonometrycznej. 

 





2

2

8

2

2

2

2

2

2















i

 

Poniewa

¿   

2

2

2

2

2











cos

, 

2

2

2

2

2







sin

, to  

4

3







. 

Mo

¿emy ju¿ napisaã postaã trygonometryczn¹: 

 



















4

3

4

3

2

2

2

2





sin

i

cos

i

 

Stosujemy teraz wz

ór Moivre’a  dla 

i

z

2

2 





  oraz 

19



n

 









i

i

sin

i

cos

sin

i

cos

sin

i

cos

i

28

28

28

28

28

19

19

2

2

2

2

2

2

2

2

4

4

2

2

4

14

4

14

2

2

4

3

19

4

3

19

2

2

2

2























































































































 

W  obliczeniach  skorzystali

œmy  z  faktu,  ¿e  liczba 



14

  jest  okresem  funkcji  sinus 

oraz cosinus. 

........................................................................................... 

 

Pierwiastkiem  algebraicznym

 

stopnia  n

  z  liczby  zespolonej 

z

  (kr

ót

ko: 

n

-tym 

pierwiastkiem z liczby 

z

) nazywamy ka

¿d¹ liczbê zespolon¹ w

 spe

ùniaj¹c¹ równanie 

z

w

n



 i u

¿ywamy oznaczenia 

n

z

. 

O  ile  pot

êgowanie  liczb  zespolonych  jest  dziaùaniem  jednoznacznym,  to 

n

z

  ma 

n

 

r

ó¿nych wartoœci, jeœli tylko 

liczba pierwiastkowana nie jest zerem. Mianowicie  

 

 
 
 
 
 
 
 
 
wz

ór 

de Moivre

’a

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

n

-ty pierwiastek 

z liczby 
zespolonej 

id3875968 pdfMachine by Broadgun Software  - a great PDF writer!  - a great PDF creator! - http://www.pdfmachine.com  http://www.broadgun.com 



















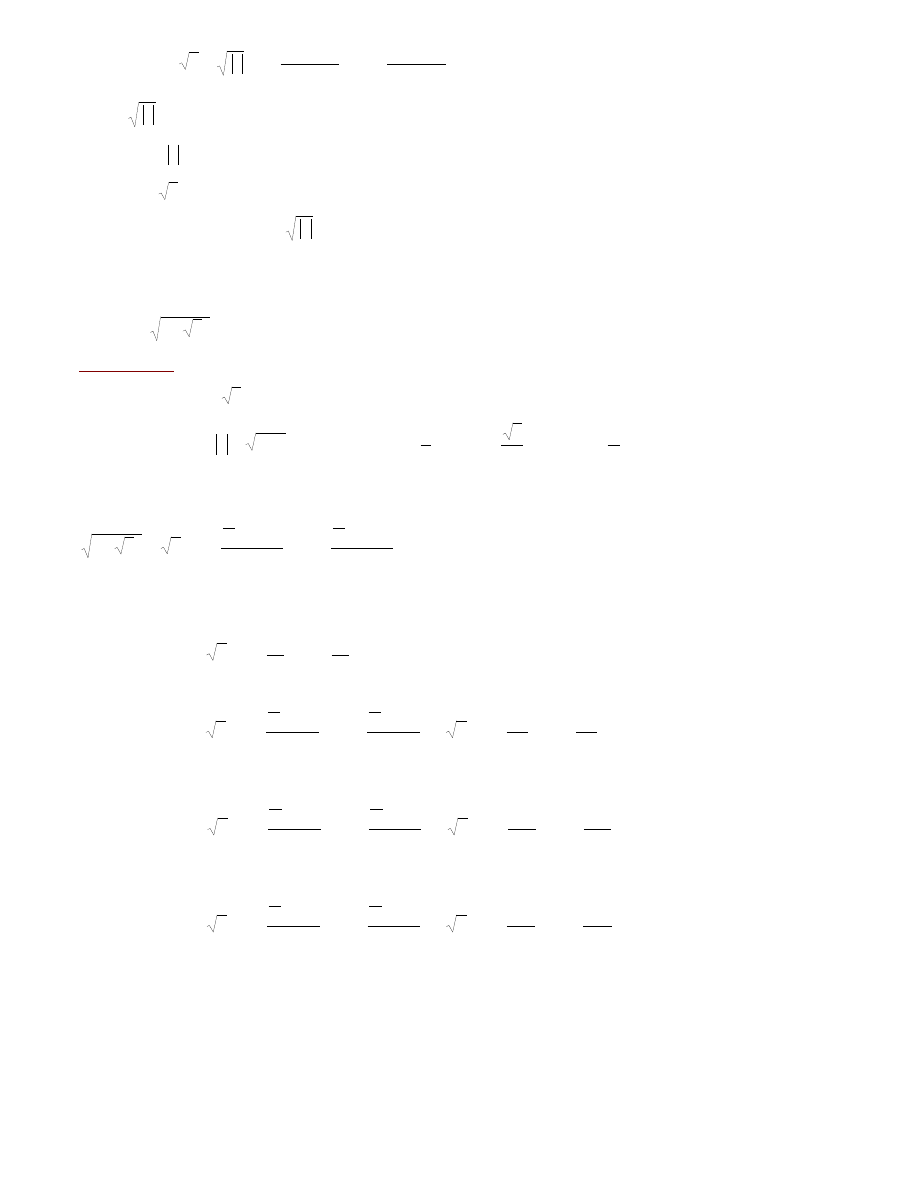
n

k

sin

i

n

k

cos

z

z

n

n









2

2

,   

k

 = 0, 1, 2, ..., 

n

1 

gdzie 

n

z

    oznacza znany  Czytelnikowi  ze  szko

ùy 

pierwiastek  arytmetyczny  liczby 

nieujemnej 

z

. 

Warto

œci 

n

z

    s

¹  liczbami  le¿¹cymi  na  okrêgu  o  œrodku  w  pocz¹tku  ukùadu 

wsp

óùrzêdnych i promieniu 

n

z

  i dziel

¹ ten okr¹g 

na n  r

ównych czêœci.

 

........................................................................................... 

PRZYK£AD

 

Obliczy

ã 

4

3

1

i



 

Rozwi

¹zanie

 

Oznaczaj

¹c 

i

z

3

1 



, znajdziemy modu

ù i argum

ent liczby z.  

Obliczamy modu

ù 

2

3

1







z

 oraz  

2

1





cos

 i 

2

3





sin

, sk

¹d 

3







. 

Teraz dla 

n

 = 4, dostajemy  



































4

2

3

4

2

3

2

3

1

4

4









k

sin

i

k

cos

i

,    

k

 = 0, 1, 2, 3. 

Warto

œci te wynosz¹

 

dla 

k

 = 0 :    















12

12

2

4

0





sin

i

cos

z

, 

dla 

k

 = 1 :    















































12

7

12

7

2

4

2

3

4

2

3

2

4

4

1













sin

i

cos

sin

i

cos

z

, 

dla 

k

 = 2 :    















































12

13

12

13

2

4

4

3

4

4

3

2

4

4

2













sin

i

cos

sin

i

cos

z

, 

dla 

k

 = 3 :    















































12

19

12

19

2

4

6

3

4

6

3

2

4

4

3













sin

i

cos

sin

i

cos

z

. 

...........................................................................................