
4. PODSTAWOWE CZŁONY AUTOMATYKI
Prawie w każdym przypadku złożony układ dynamiczny można rozpatrywać jako zespół
odpowiednio ze sobą połączonych członów elementarnych, a więc charakteryzujących się
najprostszymi właściwościami dynamicznymi. Takie elementarne człony noszą nazwę
podstawowych elementów automatyki. Wyróżnimy podstawowe grupy tych elementów:
- bezinercyjne (proporcjonalne),
- inercyjne:
pierwszego rzędu,
oscylacyjne,
dwuinercyjne
- całkujące:
idealne,
rzeczywiste,
izodromowe
- różniczkujące:
idealne,
rzeczywiste,
- opóźniające.
Poniżej zostaną one szczegółowo omówione. Wszystkie wykresy prezentowane w tym
rozdziale wykonane zostały dla konkretnych danych liczbowych z wykorzystaniem programu
CorelDRAW9 i Matlab 4.
4.1. Człon proporcjonalny ( bezinercyjny )
Najprostszym członem układów dynamicznych jest człon proporcjonalny. Charakteryzuje
go równanie wiążące sygnał wyjściowy z sygnałem wejściowym
)
(
)
(
t
x
k
t
y
(4.1)
a transmitancja operatorowa ma postać
k
s
x
s
y
s
G
)
(
)
(
)
(
(4.2)
gdzie: y – wielkość wyjściowa, x – wielkość wejściowa.
Jego właściwości są charakteryzowane jedynie przez współczynnik wzmocnienia k. Człon
ten nie ma zdolności pamiętania stanów czy sygnałów poprzedzających chwile obserwacji, o
wartości sygnału wyjściowego w chwili t decyduje tylko wartość sygnału wejściowego w tej
samej chwili t . Nie możemy więc w tym przypadku mówić o stanie układu ani o równaniu stanu.
Dlatego człon ten często jest również nazywany członem bezinercyjnym.
Równanie charakterystyki statycznej ma postać
x
k
y
lub
,
0
0
C
x
k
y
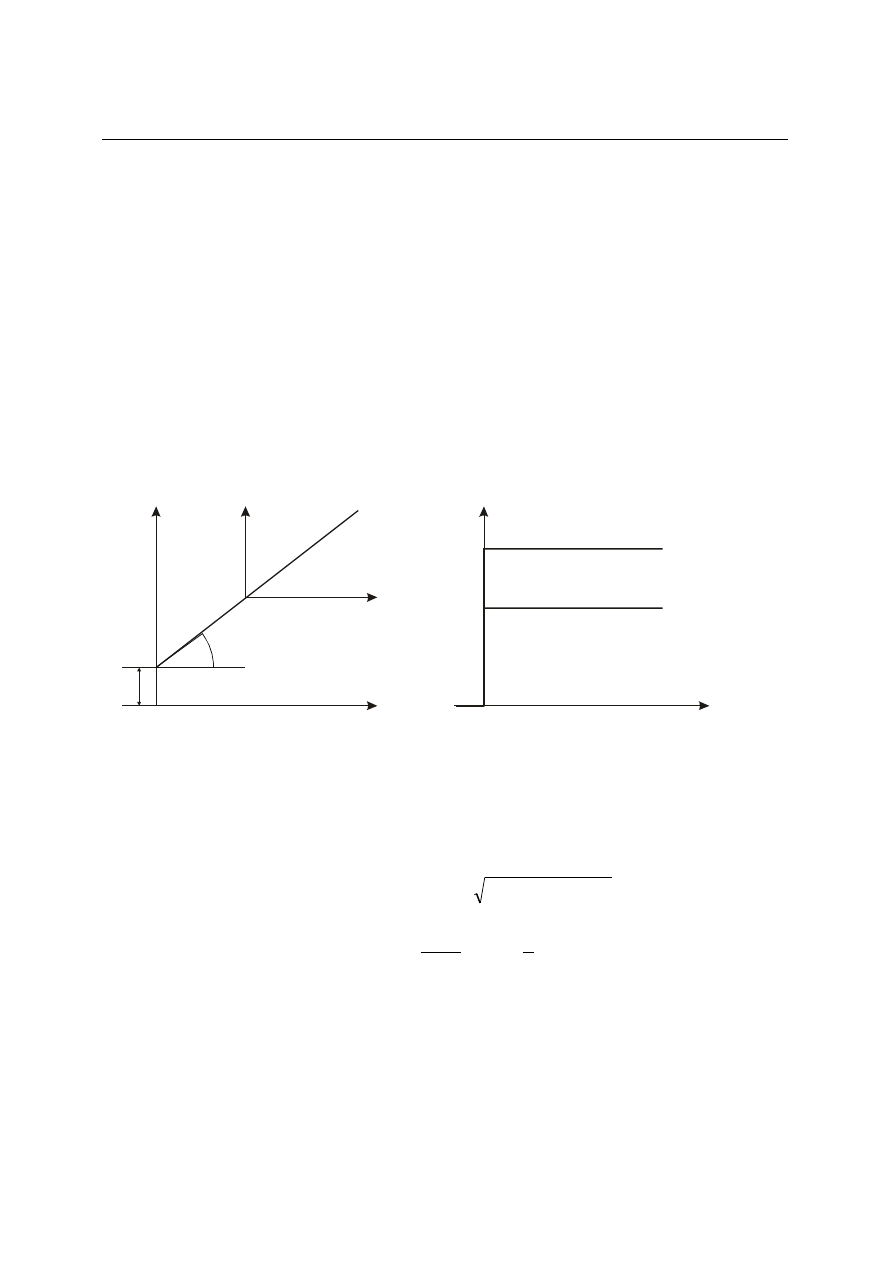
69
4. Podstawowe człony automatyki
gdzie C jest stałą określającą przesunięcie charakterystyki w stosunku do początku układu
współrzędnych.
Odpowiedź na wymuszenie skokowe
a
t
t
x
)
(
1
)
(
będzie
.
)
(
1
)
(
a
k
t
t
y
Wykresy obrazujące charakterystykę statyczną i skokową elementu bezinercyjnego przedstawione
są na rys. 4.1.
Transmitancja widmowa elementu bezinercyjnego ma postać:
.
)
(
k
j
G
(4.3)
Część rzeczywista i urojona
)
(
j
G
:
.
0
)
(
,
)
(
Q
k
P
(4.4)
Logarytmiczne charakterystyki amplitudowa i fazowa:
,
log
20
)
(
)
(
log
20
)
(
log
20
)
(
2
2
k
Q
P
M
L
(4.5)
.
0
0
tg
)
(
)
(
tg
)
(
k
arc
P
Q
arc
(4.6)
Rysunek 4.2 przedstawia wykresy omawianych charakterystyk.
y
0
x
0
C
arc tg k
y
x
x
k
h(t)
h(t)
k>1
t
0
x(t)= (t)
1
a)
b)
Rys. 4.1. - charakterystyka statyczna elementu bezinercyjnego (zaznaczono oba układy
współrzędnych, w jakich można przedstawić charakterystykę, - charakterystyka skokowa
(odpowiedź na wymuszenie skokowe) dla >1
a)
b)
k
a
a
a

Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
70
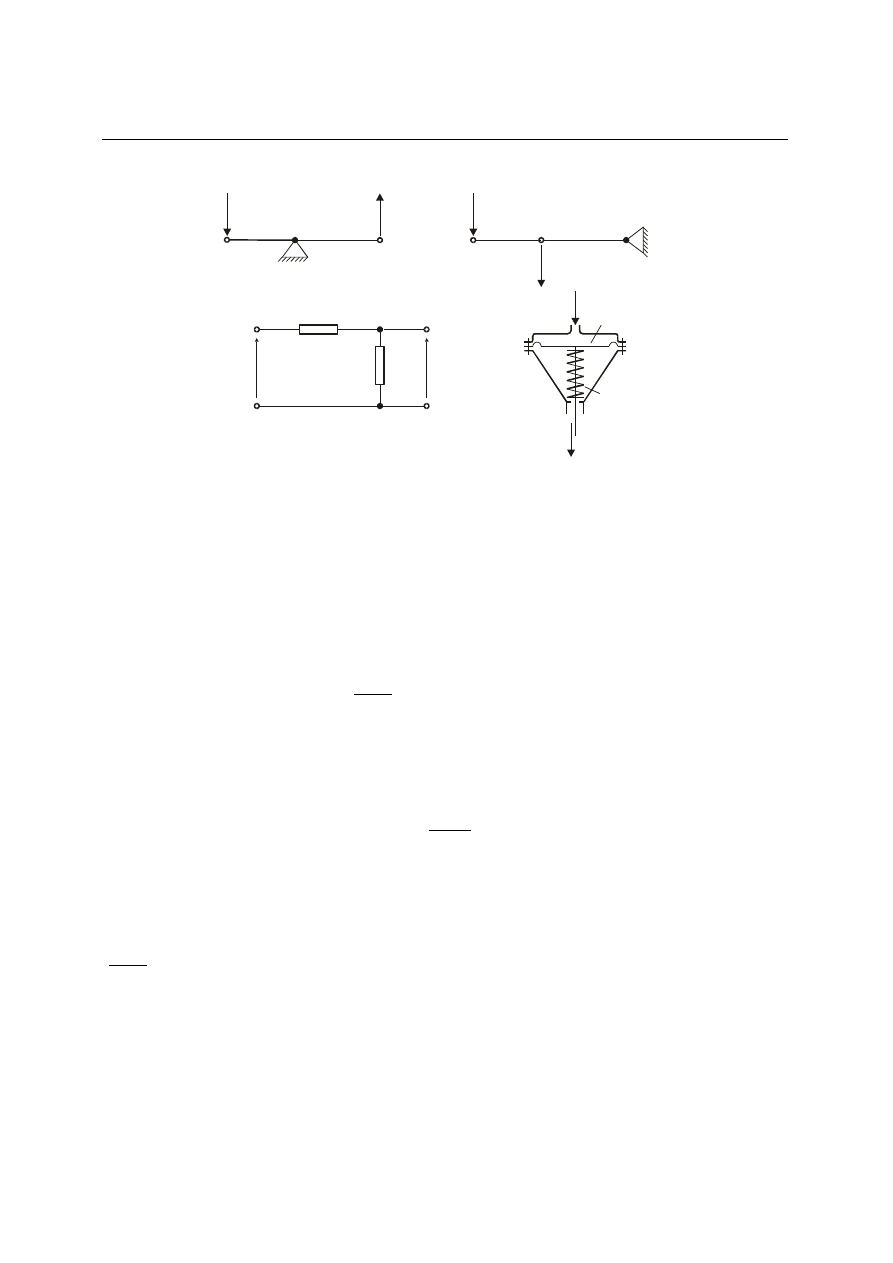
Przykłady kilku elementów bezinercyjnych podano na rys. 4.3, a niżej zestawione
zostały równania tych elementów.
1. Jeżeli sygnał wejściowy x i wyjściowy y są przesunięciami (rys. 4.3a) mamy
Jeżeli sygnał wejściowy F
x
i wyjściowy F
y
są siłami (rys. 4.3a), mamy
2. Przy analogicznych oznaczeniach jak w przykładzie 1 (rys. 4.3b) otrzymamy
3. Zakładając brak obciążenia i oznaczając U
1
, U
2
- napięcia wejścia i wyjścia, R
1
, R
2
-
rezystancje (parametry układu), otrzymamy (rys. 4.3c)
4. Jeżeli pominiemy masę części ruchomych i tarcie lepkie oraz oznaczymy: A[m
2
]-
powierzchnia efektywna (czynna) membrany, p[N/m
2
] - ciśnienie, c[N/m] - sztywność sprężyny,
y[m] - przesunięcie trzpienia siłownika, to wyjście y związane będzie z wejściem p zależnością
proporcjonalną (rys. 4.3c)
.
)
(
)
(
)
(
,
c
A
s
x
s
y
s
G
p
c
A
y
.
a
b
=
)
(s
x
)
(s
y
=
)
(s
G
,
x
a
b
=
y
.
b
a
=
)
(s
x
)
(s
y
=
)
(s
G
,
F
b
a
=
F
x
y
.
b
b
+
a
=
)
(s
F
)
(s
F
=
)
(s
G
,
F
b
b
+
a
=
F
,
b
+
a
b
=
)
(s
x
)
(s
y
=
)
(s
G
,
x
b
+
a
b
=
y
x
y
x
y
.
R
+
R
R
=
)
(s
U
)
(s
U
=
)
(s
G
,
U
R
+
R
R
=
U
2
1
2
1
2
1
2
1
2
2
k>1
0
a)
b)
Rys. 4.2.Charakterystyki częstotliwościowe elementu bezinercyjnego:
charakterystyka
amplitudowo-fazowa, - logarytmiczna charakterystyka amplitudowa i fazowa
a) -
b)
k
G(j
(
(
)
)
)
Q
P
0,1
0,1
1,0
1,0
10
10
100
100
L
dB
20log k
0 o
71
4. Podstawowe człony automatyki
4.2. Człony inercyjne
Człon inercyjny pierwszego rzędu
Człon inercyjny pierwszego rzędu (krótko: człon inercyjny) jest opisany równaniem
)
(
)
(
)
(
t
x
k
t
y
dt
t
dy
T
(4.7)
przy czym:
T - stała czasowa;
k - współczynnik wzmocnienia
a transmitancja operatorowa ma postać
Ts
k
s
G
1
)
(
(4.8)
Człony tego typu występują bardzo często w przyrodzie, gdyż charakteryzują proces
gromadzenia masy i energii z oddziaływaniem wstecznym.
Równanie charakterystyki statycznej otrzymamy z równania (4.7) przyjmując pochodną
dt
t
dy )
(
równą zero. Będzie ono miało postać:
.
x
k
y
Wykres tej charakterystyki jest identyczny jak podany na rys. 4.1a.
Odpowiedź na wymuszenie skokowe
a
t
t
x
)
(
1
)
(
obliczymy posługując się tabl. 3.1.
Z definicji mamy:
x
x
y
y
y
a
a
b
b
F
x
F
x
F
y
F
y
u
1
u
2
R
1
R
2
c
A
a)
b)
c)
d)
p
Rys. 4.3. Przykłady elementów bezinercyjnych (proporcjonalnych):
-dźwignie, - dzielnik napięcia,
siłownik pneumatyczny
a,b)
c)
d) -
.
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
72
)
(
)
(
L
)
(
1
s
x
s
G
t
y
Dla wymuszenia skokowego o amplitudzie a,
a
s
s
x
1
)
(
. A zatem wzór na charakterystykę
skokową elementu inercyjnego przyjmie postać:
,
1
1
1
1
1
1
)
(
)
(
1
1
1
T
t
e
aT
T
k
T
s
s
a
T
k
a
s
Ts
k
a
s
s
G
t
h
L
L
L
ostatecznie
.
1
)
(
T
t
e
a
k
t
h
(4.8)
0
0
1
2
5
10
15
20
25
30
T
T
x(t)= (t)a
1
0,632ka
ka
t [s]
h(t)
h( )
a=1
k=2
T=5
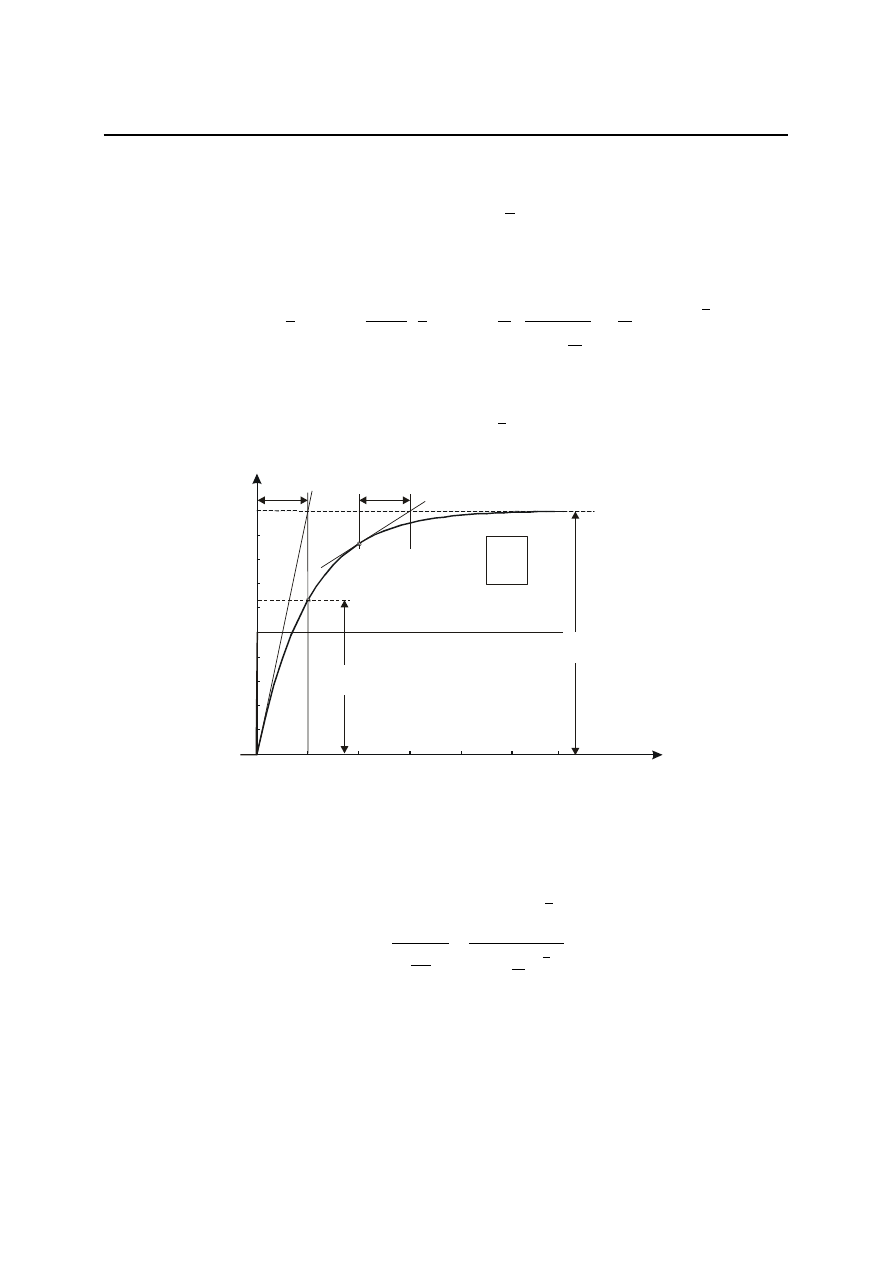
Rys. 4.4. Odpowiedź elementu inercyjnego pierwszego rzędu na wymuszenie skokowe
Stałą czasową T można określić z wykresu, przeprowadzając styczną w dowolnym punkcie
krzywej wykładniczej h(t) i wyznaczając odcinek podstycznej na asymptocie
.
1
1
T
e
T
a
k
e
a
k
dt
dh
h
a
k
podstyczna
T
t
T
t
Stałą czasową T można również określić jako czas od chwili t = 0 do chwili, kiedy h(t)
osiąga 63,2% swojej końcowej wartości ustalonej ka. Podstawiając t = T otrzymamy
.
632
,
0
1
)
(
1
a
k
e
a
k
T
h
Wartość współczynnika wzmocnienia elementu inercyjnego określamy z wykresu

73
4. Podstawowe człony automatyki
charakterystyki skokowej jako stosunek h(
)/a, gdzie h(
) przedstawia maksymalną wartość
charakterystyki skokowej (dla t
) równą ka.
Wykres charakterystyki skokowej elementu inercyjnego o transmitancji
s
s
G
5
1
2
)
(
wraz z konstrukcjami geometrycznymi, obrazującymi sposoby wyznaczenia jego parametrów
przedstawiony jest na rys. 4.4.
Transmitancja widmowa elementu inercyjnego ma postać:
T
j
k
s
G
j
G
j
s
1
)
(
)
(
(4.9)
Część rzeczywistą i urojoną
)
(
j
G
wyznaczamy mnożąc licznik i mianownik
transmitancji przez liczbę zespoloną sprzężoną z mianownikiem
2
2
2
2
1
1
1
1
1
T
kT
j
k
T
T
j
T
j
kT
j
k
T
j
T
j
T
j
k
Stąd
2
2
2
2
1
)
(
,
1
)
(
T
kT
Q
T
k
P
(4.10)
Wykres G(j
) ma postać półokręgu o średnicy k, ze środkiem w punkcie (k/2, j0) (rys.
4.5). Przy zmianie wartości stałej czasowej T kształt krzywej pozostaje taki sam, zmienia się
jedynie rozkład punktów odpowiadających pulsacjom
1
,
2
itd.
Rys. 4.5. Charakterystyka amplitudowo-fazowa G(j
) członu inercyjnego
Logarytmiczna charakterystyka amplitudowa ma postać:
.
1
log
20
)
(
)
(
log
20
)
(
log
20
)
(
2
2
2
2
T
k
Q
P
M
L
Im[G(j )] = Q( )
Re[G(j )] = P( )
h
T
k
1,0
2,0
-1,0
-0,5
k=2
T=5
0
0,5
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
74
Ostatecznie
.
1
log
20
log
20
)
(
2
2
T
k
L
(4.11)
Wykres L(
) można uprościć, pomijając we wzorze (4.11) dla
<1/T składnik T
2
2
, a dla
> 1/T składnik 1 pod pierwiastkiem. Otrzymamy wówczas tzw. asymptotyczną logarytmiczną
charakterystykę amplitudową :
.
log
20
log
20
)
(
/
1
,
log
20
)
(
/
1
T
k
L
T
dla
k
L
T
dla
(4.12
Pulsacja (częstotliwość kątowa)
= 1/T nazywa się pulsacją sprzęgającą i oznacza się ją
symbolem
s
lub
0
.
Wykresy rzeczywistej i asymptotycznej charakterystyki amplitudowej przedstawione są na
rys. 4.6a. Nachylenie opadającego odcinka charakterystyki asymptotycznej (dla
> 1/T )
określimy obliczając przyrost L(
) na dekadę:
dB
T
k
T
k
L
L
20
10
log
20
)
(
log
20
log
20
)
10
(
log
20
log
20
)
(
)
10
(
(4.13)
Rys. 4.6. Logarytmiczne charakterystyki elementu inercyjnego pierwszego rzędu
G
a
in
d
B
G
a
in
d
B
P
h
a
s
e
d
e
g
10
-2
10
-2
10
-1
10
-1
10
0
10
0
10
1
10
1
-90
-60
-30
0
-40
-20
0
20
L( )
dB
20log k
-20dB/dek
1
2
1
2
0,02
0,02
0,05
0,05
0,1
0,1
0,3
0,3
0,5
0,5
1,0
1,0
2
2
3
3
4
4
6
6
8
8
o
o
o
o
[rad/sek]
[rad/sek]
s
= 1/T
k=2
T=5

75
4. Podstawowe człony automatyki
1
5
2
)
(
s
s
G
, a) – charakterystyka amplitudowa, b) – charakterystyka fazowa
W praktyce, przy obliczeniach wstępnych posługujemy się charakterystykami
asymptotycznymi, a przy obliczeniach dokładnych charakterystykami rzeczywistymi, które
otrzymujemy w wyniku dokładnych obliczeń, najczęściej przy pomocy odpowiedniego
oprogramowania komputerowego (programów symulacyjnych).
Logarytmiczna charakterystyka fazowa elementu inercyjnego
.
)
tg(
)
tg(
)
(
)
(
tg
)
(
T
arc
T
arc
P
Q
arc
(4.14)
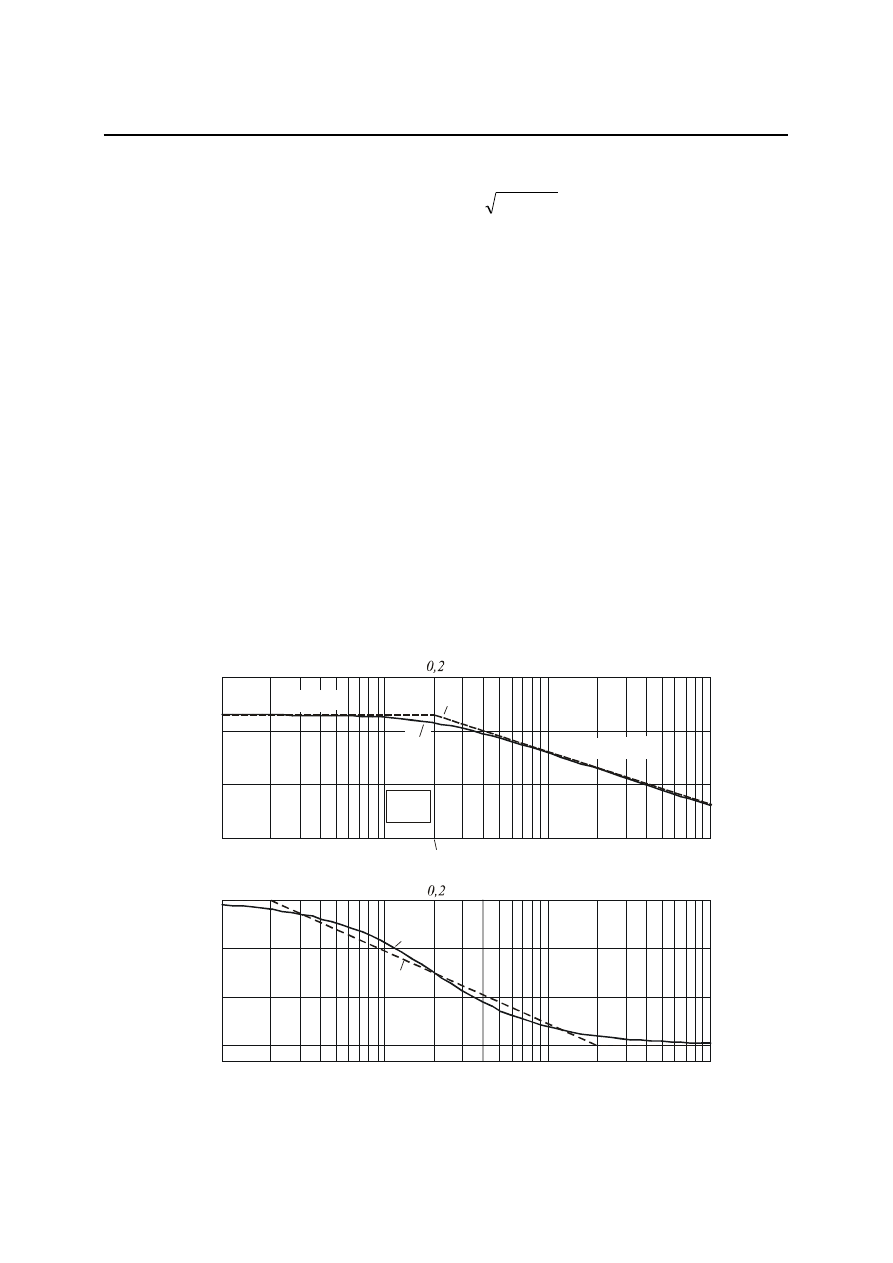
Wykres
)
(
przedstawiony jest na rys. 4.6b. Na wykresie oprócz charakterystyki
rzeczywistej przedstawiono liniami przerywanymi stosowane niekiedy aproksymacje
trójodcinkowe krzywej
)
(
. Aproksymacja
)
(
a
polega na zastąpieniu środkowego odcinka
krzywej
)
(
prostą, bliską stycznej do
)
(
w jej punkcie przegięcia (ściśle, styczna osiąga 0
dla
81
,
4
/
1
/
s
oraz -90
dla
81
,
4
/
s
, natomiast
)
(
a
osiąga 0
dla
2
,
0
5
/
1
/
s
oraz -90
dla
5
/
s
, co ułatwia jej wykreślanie). Aproksymacja
)
(
b
polega na zastąpieniu
środkowego odcinka krzywej
)
(
sieczną przechodzącą przez 0
dla
1
,
0
/
s
oraz -90
dla
10
/
s
.
Przykłady członu inercyjnego
1. Typowym przykładem członu inercyjnego jest kondensator ładowany przez rezystor (rys.
4.7). Z prawa Ohma możemy zapisać zależność na u
1
(t) jako sumę spadku napięcia na rezystorze
R i kondensatorze C. Wartość prądu płynącego przez kondensator zależy od pojemności tego
kondensatora i prędkości zmian napięcia na jego okładzinach. Otrzymamy:
.
)
(
)
(
,
)
(
)
(
)
(
2
2
1
dt
t
du
C
t
i
t
u
R
t
i
t
u
u
1
u
2
R
C
i(t)
(t)
(t)
Rys. 4.7. Schemat prostego członu inercyjnego RC
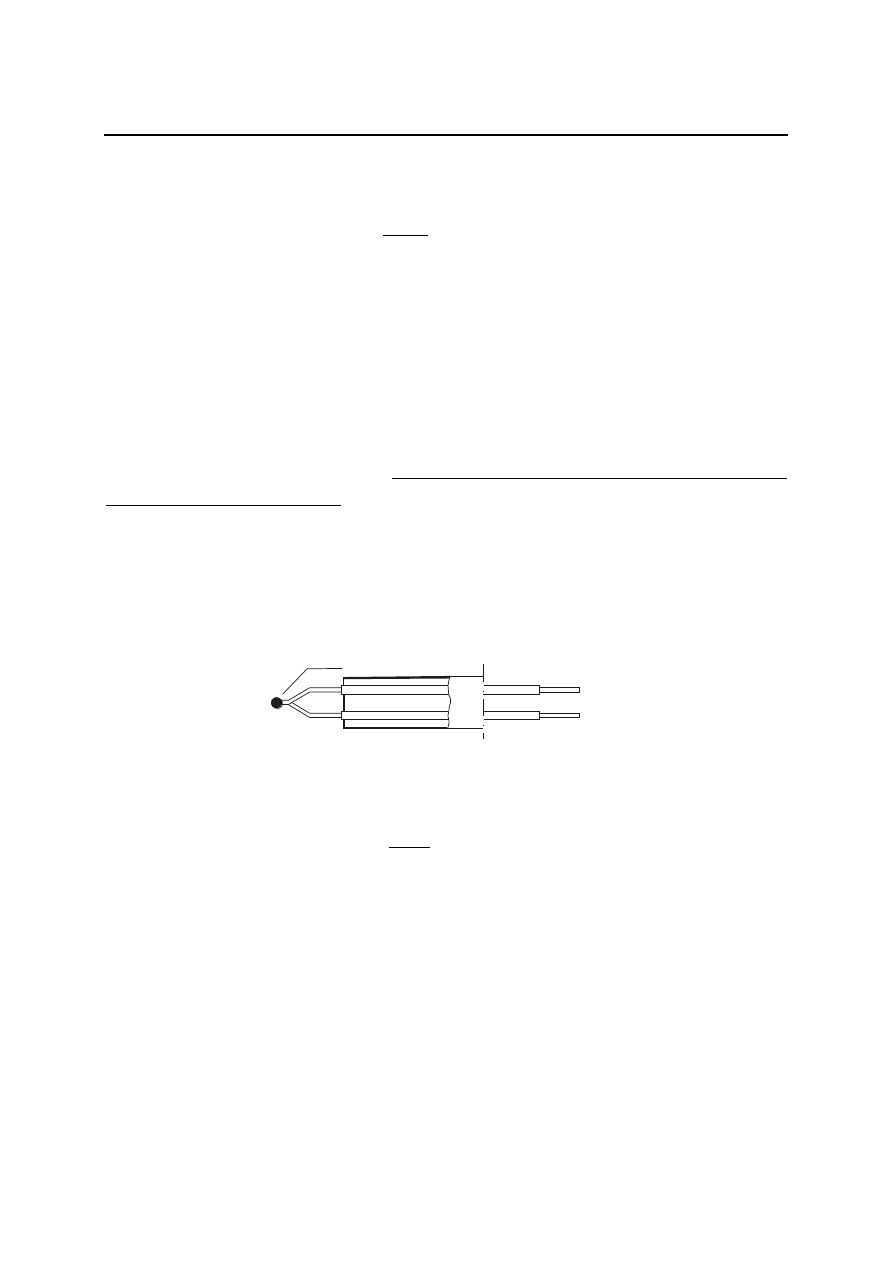
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
76
Podstawiając drugie równanie do pierwszego i zapisując człony związane z sygnałem
wyjściowym po lewej stronie znaku równości a pozostałe po prawej otrzymamy
.
)
(
)
(
)
(
1
2
2
t
u
t
u
dt
t
du
RC
Fakt, że iloczyn RC posiada rozmiar sekundy ( [Ω
F] = [V/A
Q/V] = [V/A
As/V] = [s] )
uzasadnia nazwanie go stałą czasową T. Po wprowadzeniu tego oznaczenia otrzymujemy
równanie analogiczne do równania 4.3.
2. Innym przykładem członu inercyjnego może być człon cieplny, np. termoelement (rys. 4.8).
Składa się on z umieszczonych w obudowie, najczęściej ceramicznej, dwóch drutów z różnych
metali. Jedne końce tych drutów są połączone spoiną, dwa pozostałe tworzą wolne tzw. zimne
końce wyprowadzone poza obudowę. Termopara taka mierzy różnicę temperatur pomiędzy
gorącymi i zimnymi jej końcami. Na skutek różnicy temperatury powstaje siła termoelektryczna
)
(
0
e
gdzie:
θ - temperatura spoiny [
];
θ
o
- temperatura zimnych końców [
];
α - współczynnik [V/
].
Rys. 4.8. Termoelement jako element inercyjny
Uproszczony model fizyczny takiego elementu otrzymamy na podstawie bilansu cieplnego
)]
(
)
(
[
)
(
1
t
t
S
dt
t
d
M
c
p
przy czym:
c
p
- ciepło właściwe termoelementu wraz z obudową umieszczoną w ośrodku o
temperaturze θ
1
(t);
m
- masa termoelementu
S
- powierzchnia wymiany ciepła (obudowy termometru);
γ
- współczynnik przewodzenia ciepła z ośrodka do wnętrza termoelementu.
Przyjmując temperaturę spoiny θ(t) zarówno jako współrzędną stanu jak i sygnał wyjściowy,
otrzymane równanie można sprowadzić do równań (4.3) i (4.5), przy czym stała czasowa
(t)
(t)
(t)
0
1
e(t)
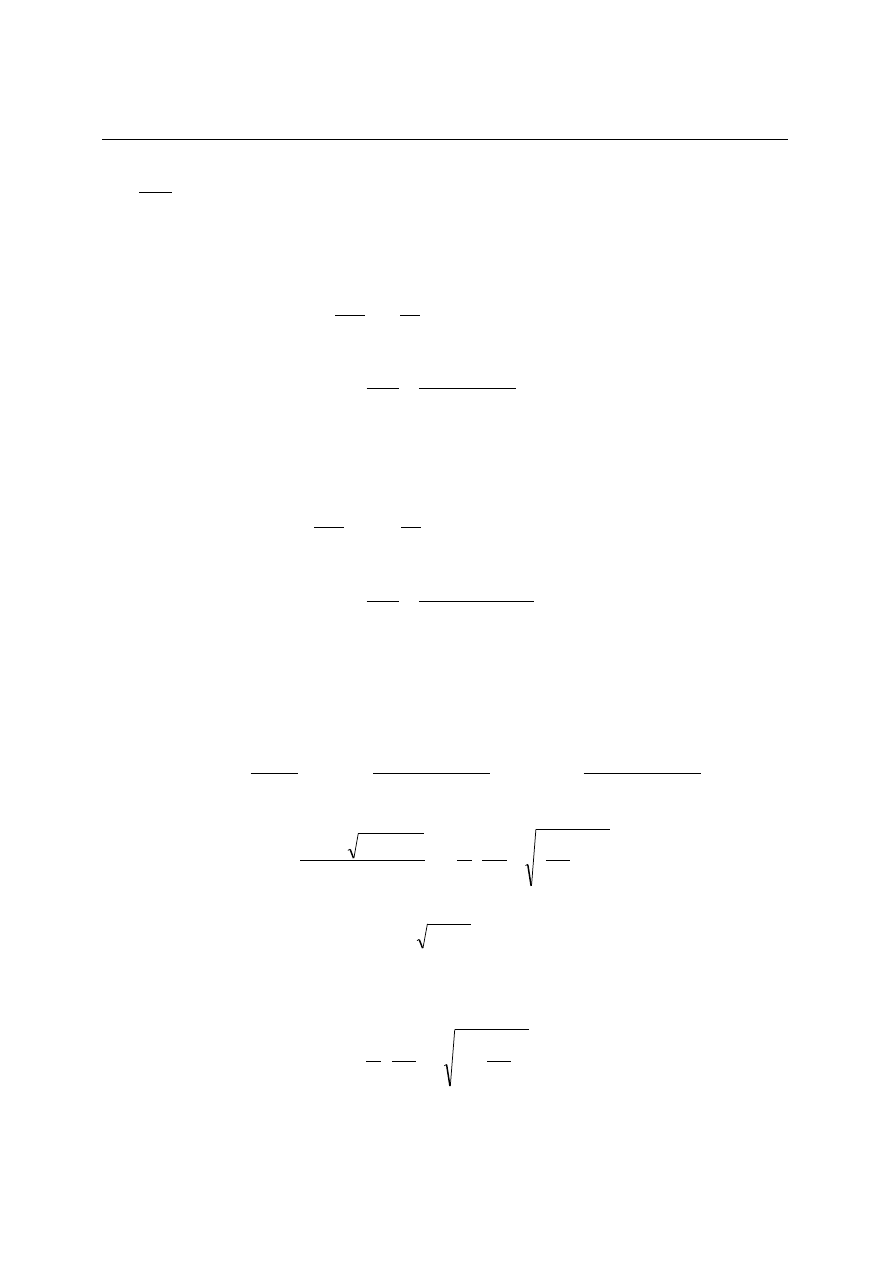
77
4. Podstawowe człony automatyki
S
m
c
T
p
, k = 1.
Człon oscylacyjny
Ogólna postać równania różniczkowego członu oscylacyjnego jest następująca:
,
2
2
2
2
1
kx
y
dt
dy
T
dt
y
d
T
(4.15)
przy czym
2
1
2
2
4T
T
. Równaniu (4.15) odpowiada transmitancja operatorowa
,
1
)
(
)
(
)
(
2
2
2
1
s
T
s
T
k
s
x
s
y
s
G
(4.16)
gdzie: k – współczynnik proporcjonalności (wzmocnienia),
T
1
, T
2
– stałe czasowe elementu.
Często stosuje się również inną postać równania różniczkowego członu oscylacyjnego,
ułatwiającą interpretację przebiegów przejściowych. Zapisuje się ją w postaci:
,
2
2
0
2
0
0
2
2
x
k
y
dt
dy
dt
y
d
(4.17)
przy czym
.
1
Wówczas transmitancja przyjmie postać:
,
2
)
(
)
(
)
(
2
0
0
2
2
0
s
s
k
s
x
s
y
s
G
(4.18)
gdzie:
1
0
/
1 T
- pulsacja oscylacji własnych elementu,
1
2
2
/ T
T
- zredukowany (względny) współczynnik tłumienia.
Charakterystyka statyczna członu oscylacyjnego będzie identyczna jak charakterystyki
Członów inercyjnych.
Odpowiedź na wymuszenie skokowe x(t)=1(t)a obliczamy z relacji:
.
)
1
(
1
)
1
(
)
(
)
(
)
(
2
2
2
1
1
2
2
2
1
1
1
s
T
s
T
s
ka
a
s
T
s
T
s
k
a
s
sM
s
L
t
h
L
L
L
Pierwiastkami wielomianu N(s) są:
1
2
2
1
2
4
2
1
2
1
2
1
2
1
2
1
2
2
2
2
,
1
T
T
T
T
T
T
T
T
T
s
(4.19)
lub dla oznaczeń przyjętych w (4.17)
.
1
2
0
2
,
1
s
(4.20)
Jeśli będzie spełniony warunek
2
1
2
2
4T
T
czyli
1
2
, charakterystyka skokowa będzie miała
oscylacyjny charakter.
Pierwiastki s
1
i s
2
zapiszemy wówczas w postaci:
2
1
2
1
2
1
2
,
1
2
1
2
1
T
T
j
T
T
T
s
(4.21)
lub
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
78
.
1
2
0
2
,
1
j
s
(4.22)
Na podstawie wzoru (3.30) otrzymamy
.
)
(
1
)
(
1
1
)
(
2
1
1
2
2
2
1
2
1
1
2
1
t
s
t
s
e
s
s
s
T
e
s
s
s
T
ka
t
h
(4.23)
Stosując wzory Eulera* oraz oznaczenia przyjęte w równaniu (4.17), charakterystykę skokową
można przedstawić w postaci:
,
1
sin
1
1
)
(
2
0
2
0
t
e
ka
t
h
t
(4.24)
gdzie
2
1
ctg
ar
.
(4.25)
Ponieważ założyliśmy współczynnik tłumienia
1
0
, więc (wobec
0
0
) wykładnik
potęgi funkcji wykładniczej jest ujemny więc amplituda oscylacji maleje. Wykres h(t) dla tego
przypadku przedstawiony jest na rys. 4.9. Składowa ustalona przebiegu wynosi ka, a składowa
przejściowa jest gasnącą sinusoidą, której okres jest stały i wynosi:
2
0
1
2
T
.
(4.26)
Dla chwil t
a
, w których kąt
a
t
2
0
1
ma wartości równe krotnościom
2
/
, a zatem h(t)
osiąga amplitudę wynikającą ze wzoru (4.24), mamy
,
19
,
15
,
11
,
7
,
3
1
1
)
(
2
1
,
17
,
13
,
9
,
5
,
1
1
1
)
(
2
1
2
2
0
2
2
0
0
0
a
a
t
a
a
t
a
a
e
ka
t
h
t
e
ka
t
h
t
(4.27)
Wynikają stąd równania obwiedni drgań h
1
(t) i h
2
(t) pokazanych na rys. 4.9.
*
).
sin
(cos
),
sin
(cos
v
j
v
e
e
v
j
v
e
e
u
jv
u
u
jv
u
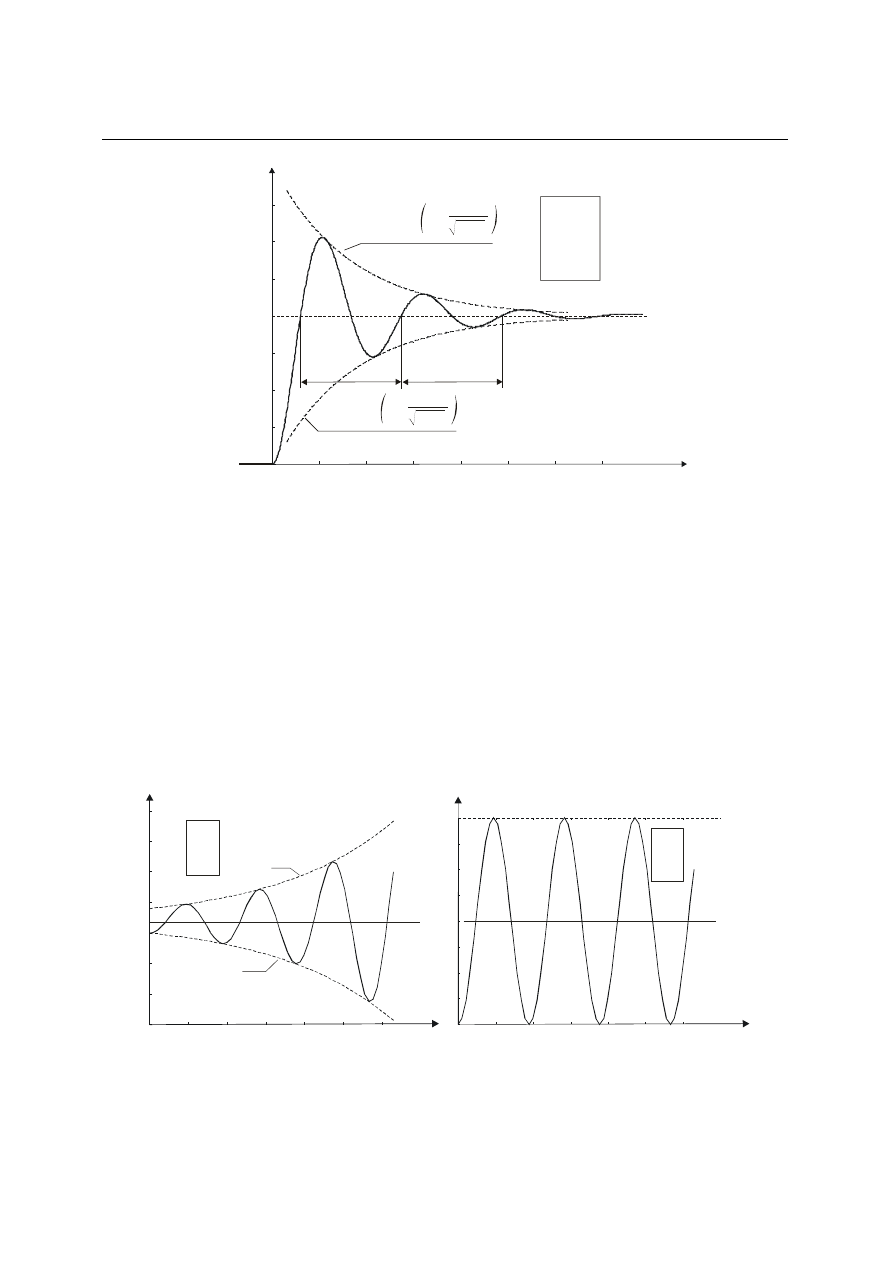
79
4. Podstawowe człony automatyki
Rys. 4.9. Odpowiedź członu oscylacyjnego na wymuszenie skokowe 1(t)a
W przypadku gdy współczynnik tłumienia jest ujemny i zgodnie z warunkiem dla
przebiegów oscylacyjnych wynosi
,
0
1
części rzeczywiste pierwiastków s
1
i s
2
są
dodatnie. Prowadzi to do związków, w których funkcje trygonometryczne są mnożone przez
funkcję wykładniczą rosnącą do nieskończoności wraz ze wzrostem czasu t. Wówczas dla
obwiedni z rys. 4.9 otrzymamy:
)
(
,
)
(
2
1
t
h
t
t
h
t
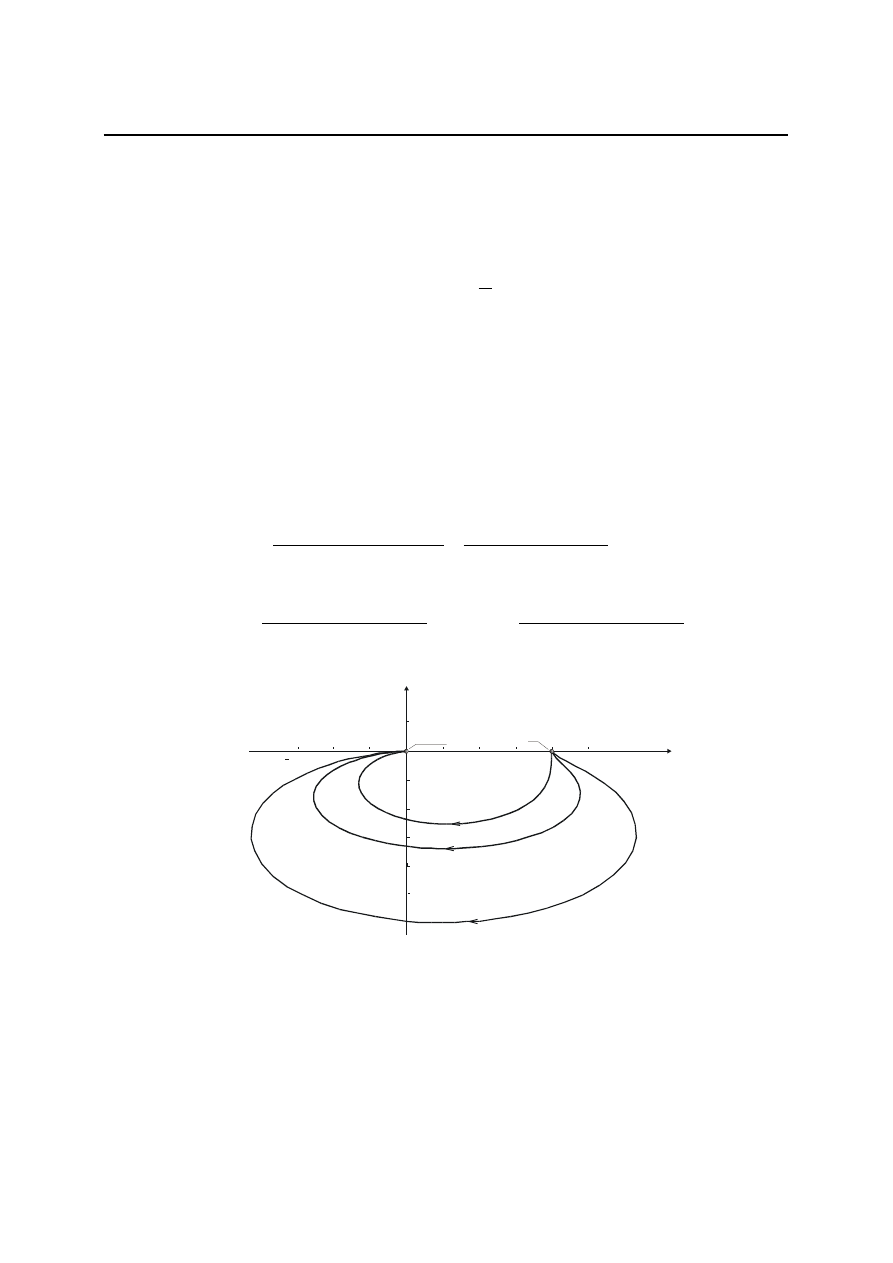
a więc odpowiedź skokowa ma charakter oscylacji o rosnącej amplitudzie (rys. 4.10a).
Rys. 4.10. Charakterystyka skokowa członu oscylacyjnego: a) przy współczynniku tłumienia z
zakresu
0
1
, b) przy współczynniku tłumienia
0
0
10
20
30
40
50
60
70
80
0.5
1
1.5
2
2.5
3
3.5
h(t)
h (t)=ka
2
h (t)=ka
1
t
1+ e
e
t
t
1-
1-
1-
T
T
ka
k=2
0
=0.3
a=1
0
1
2
3
4
5
6
7
-15
-10
-5
0
5
10
15
20
h (t)
1
h (t)
2
a=1
k=2
0
=.3
h(t)
t
0
1
2
3
4
5
6
7
0
0.5
1
1.5
2
2.5
3
3.5
4
h(t)
t
a=1
k=2
0
=0.3
2ka
ka
a)
b)
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
80
W przypadku szczególnym, kiedy współczynnik tłumienia jest równy zeru (
0
tzn. T
2
= 0), co odpowiada przypadkowi członu idealnego, w którym nie występują straty energii, części
rzeczywiste pierwiastków s
1
i s
2
są równe zeru i charakterystyka skokowa ma charakter oscylacji
nietłumionych (drgania zachowawcze o pulsacji
0
) o stałej amplitudzie (rys. 4.10b):
2
sin
1
)
(
0
t
ka
t
h
(4.28)
Jeżeli
)
1
(
4
2
2
1
2
2
T
T
, to pierwiastki s
1
i s
2
są ujemne rzeczywiste i przebieg h(t) traci
charakter oscylacyjny. Również w przypadku, kiedy występuje tłumienie krytyczne a więc
1
4
2
2
1
2
2
T
T
, mamy podwójny, ujemny pierwiastek rzeczywisty, co odpowiada
aperiodycznemu przebiegowi. Dokładna analiza tych przypadków przeprowadzona jest w
rozdziale omawiającym człon inercyjny drugiego rzędu.
Transmitancja widmowa członu oscylacyjnego wyznaczona na podstawie transmitancji
operatorowej (4.18) ma postać:
,
2
)
(
2
)
(
)
(
0
2
2
0
2
0
2
0
0
2
2
0
j
k
j
j
k
j
G
(4.29)
Część rzeczywista i urojona
:
)
(
j
G
.
)
2
(
)
(
2
)
(
,
)
2
(
)
(
)
(
)
(
2
0
2
2
2
0
3
0
2
0
2
2
2
0
2
2
0
2
0
k
Q
k
P
(4.30)
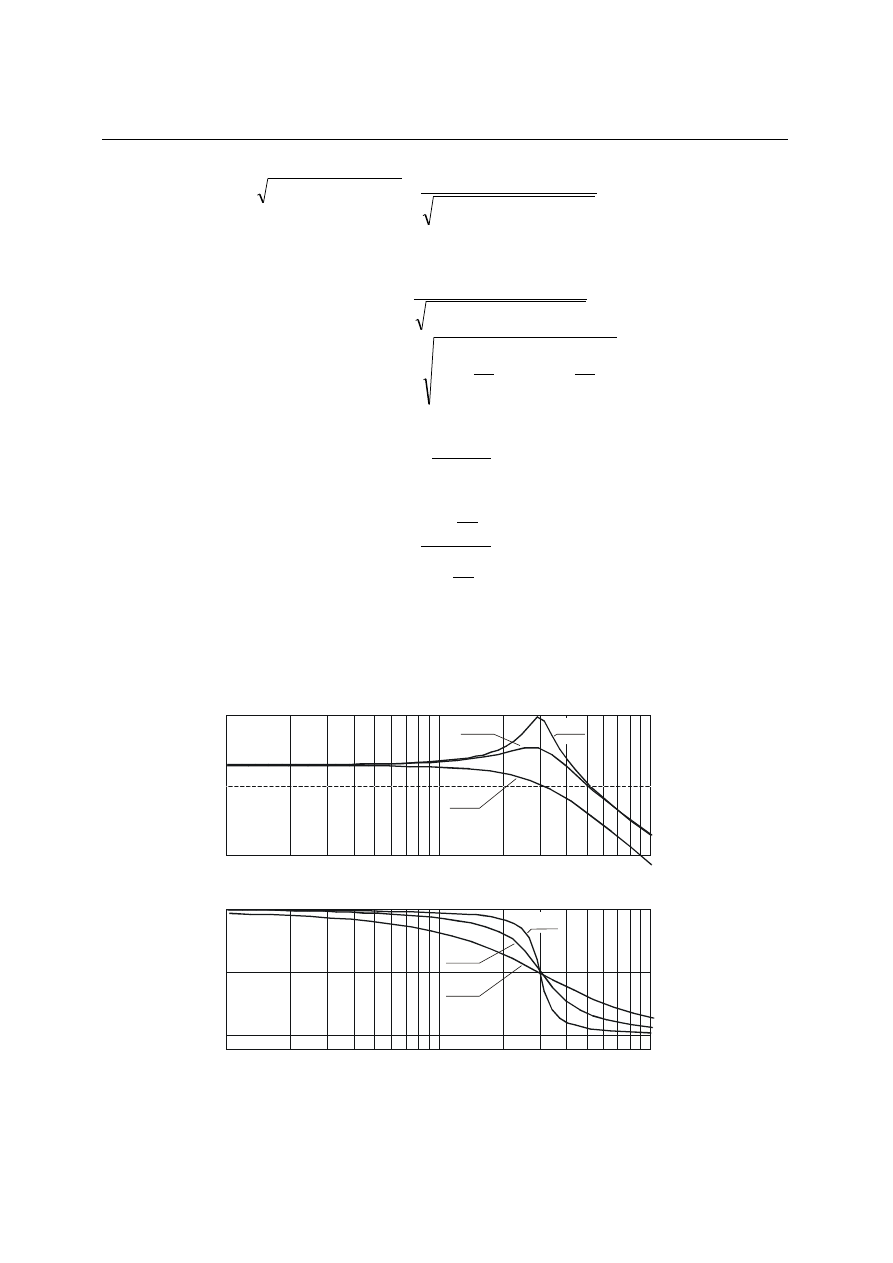
Rys. 4.11. Charakterystyki amplitudowo-fazowe członu oscylacyjnego dla różnych
wartości współczynnika tłumienia
Wykres
)
(
j
G
przedstawiono na rys. 4.11. Wykres ten zaczyna się w punkcie P(0) = k,
Q(0) = 0 przy
= 0 i kończy się przy
= +
w punkcie P(+
) = 0, Q(+
) = 0. Charakterystyka
ta jest krzywą, której przebieg – przy danych wartościach k i
0
– zależy od współczynnika
tłumienia
. Przecina ona oś urojoną w punkcie P(
0
)= 0, Q(
0
) =
2
/
k
.
Moduł transmitancji widmowej
-1
-0.5
0
0.5
1
1.5
1.5
2
2.5
-4
-5
-3
-2
-1
1
P( )
Q( )
k
h
81
4. Podstawowe człony automatyki
2
0
2
2
2
0
2
0
2
2
2
))
(
(
))
(
(
)
(
k
Q
P
M
(4.31)
Logarytmiczna charakterystyka amplitudowa
,
2
log
20
)
(
2
0
2
2
2
0
2
0
k
L
(4.32)
.
2
1
log
20
log
20
)
(
2
0
2
2
0
k
L
(4.32a)
Logarytmiczna charakterystyka fazowa:
,
2
tg
)
(
2
2
0
0
arc
(4.33)
.
1
2
tg
)
(
2
0
0
arc
(4.33a)
Wykresy charakterystyk logarytmicznych członu oscylacyjnego dla różnych wartości
współczynnika tłumienia przedstawione zostały na rys. 4.12.
Rys. 4.12. Charakterystyki logarytmiczne członu oscylacyjnego
10
10
-2
-2
10
10
-1
-1
10
10
0
0
-20
-90
-180
0
0
20
Frequency (rad/sec)
Frequency (rad/sec)
L( )
dB
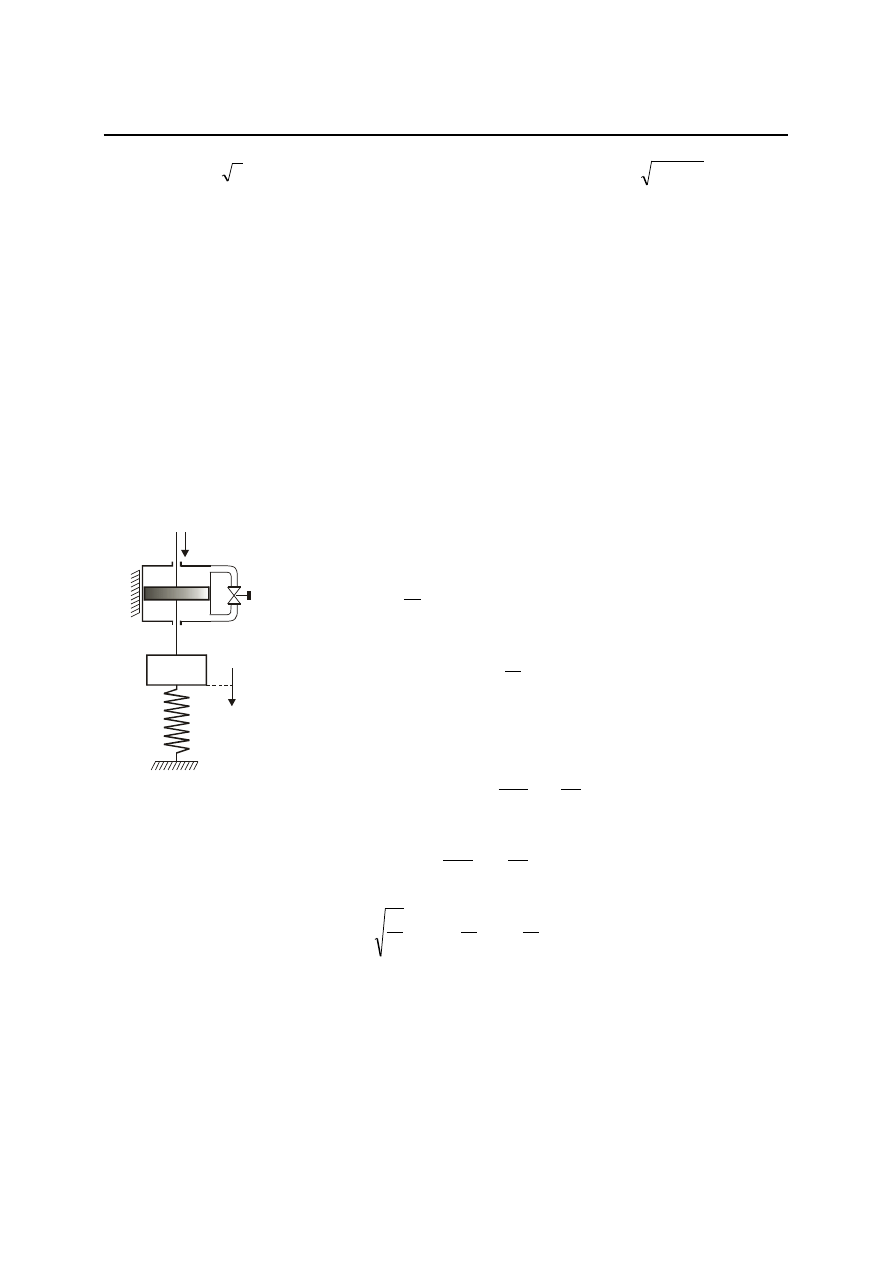
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
82
Dla
2
/
2
charakterystyka L(
) osiąga maksimum przy
2
0
2
1
/
, przy czym
wartość tego maksimum jest tym większa, im mniejszą wartość ma zredukowany współczynnik
tłumienia
. Dla
= 0 maksimum występuje przy
1
/
0
i ma wartość nieskończenie wielką.
Ze względu na nieregularny kształt charakterystyk L(
) aproksymacja za pomocą
charakterystyk asymptotycznych jest stosowana tylko przy obliczeniach wstępnych, dla
1
3
,
0
(wówczas błąd aproksymacji nie przekracza wartości 6 dB).
Przy zmianie
od 0 do
przesunięcie fazowe zmienia się od 0 do -180
, przy czym dla
1
/
0
wynosi zawsze -90
.
Przykład członu oscylacyjnego. Zespół masa – tłumik - sprężyna.
Schemat takiego zespołu podano na rys. 4.13. Sygnałem wejściowym jest siła F, sygnałem
wyjściowym jest przesunięcie masy y.
W stanie ustalonym siła F oraz ciężar mg są równoważone siłą wywieraną przez ugiętą
sprężynę. Warunek ten zapiszemy następująco:
0
0
y
c
mg
F
s
,
skąd
.
1
0
0
mg
F
c
y
s
(4.34)
Odchylenie masy m z położenia równowagi
F
c
y
s
1
.
(4.35)
W stanach nieustalonych, uwzględniając założenia
upraszczające podane w punkcie 2.2, otrzymamy następujące równanie
równowagi:
,
2
2
y
c
dt
dy
c
dt
y
d
m
F
s
t
skąd
,
2
2
2
2
1
kF
y
dt
dy
T
dt
y
d
T
(4.36)
gdzie:
.
1
,
,
2
1
s
s
t
s
c
k
c
c
T
c
m
T
Człon inercyjny drugiego rzędu
Jeżeli w członie oscylacyjnym, opisanym przez równanie (4.15) współczynnik tłumienia
1
, to równanie charakterystyczne ma pierwiastki rzeczywiste ujemne (4.22) i człon ten staje
się członem inercyjnym drugiego rzędu, zwanym dwuinercyjnym.
F
m
c
t
c
s
y
Rys. 4.13. Zespół
masa-tłumik-sprężyna
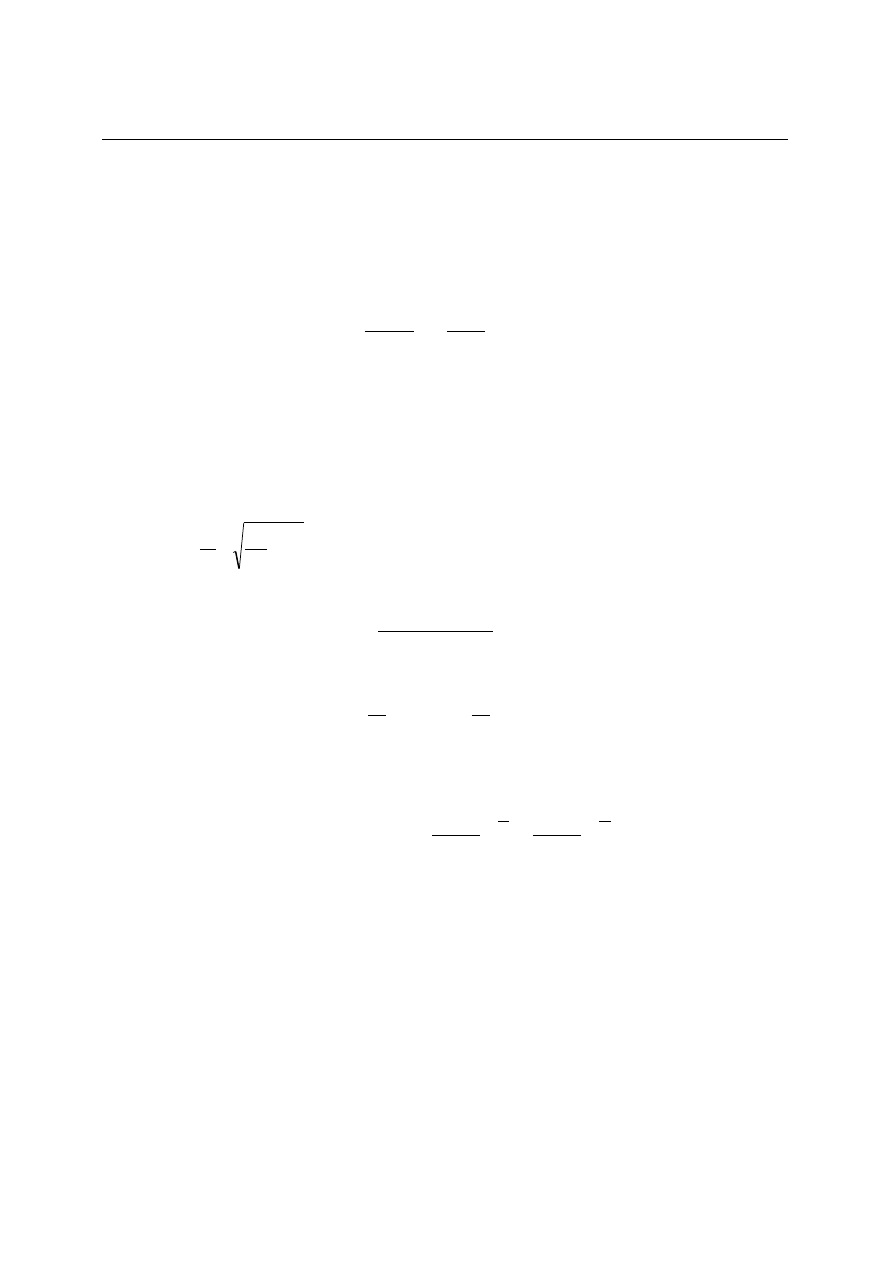
83
4. Podstawowe człony automatyki
Przez człon dwuinercyjny będziemy rozumieli połączenie szeregowe dwóch członów
inercyjnych. Z tego punktu widzenia można by pominąć jego omawianie. Istnieją jednak układy
dynamiczne, w których te dwa człony inercyjne są ściśle ze sobą powiązane; dlatego omówimy
taki człon oddzielnie. Równanie charakteryzujące człon dwuinercyjny jako zależność sygnału
wyjściowego od wejściowego przedstawimy w postaci
)
(
)
(
)
(
)
(
1
2
2
2
2
t
x
k
t
y
dt
t
dy
T
dt
t
y
d
T
(4.37)
Równanie charakterystyczne tego układu
0
1
1
2
2
2
s
T
s
T
powinno mieć pierwiastki
rzeczywiste. Zapewnia to warunek
.
2
2
1
T
T
W postaci operatorowej równanie (4.37) zapiszemy
)
(
)
(
)
1
(
1
2
2
2
s
x
k
s
y
s
T
s
T
.
(4.38)
Lewą stronę równania (4.38) można zapisać w innej formie
)
(
)
(
)
1
)(
1
(
4
3
s
x
k
s
y
s
T
s
T
(4.39)
gdzie:
.
4
2
2
2
2
1
1
4
,
3
T
T
T
T
Transmitancja operatorowa członu dwuinercyjnego ma postać
.
)
1
)(
1
(
)
(
4
3
s
T
s
T
k
s
G
(4.40)
Pierwiastki równania charakterystycznego są rzeczywiste i wynoszą:
.
1
,
1
4
2
3
1
T
s
T
s
Przebiegi czasowe tego członu są więc aperiodyczne.
Wzór na charakterystykę skokową znajdziemy bezpośrednio z tablic przekształceń Laplace’a
.
1
)
(
4
3
1
4
3
4
1
3
4
3
t
T
t
T
e
T
T
T
e
T
T
T
a
k
t
h
(4.41)
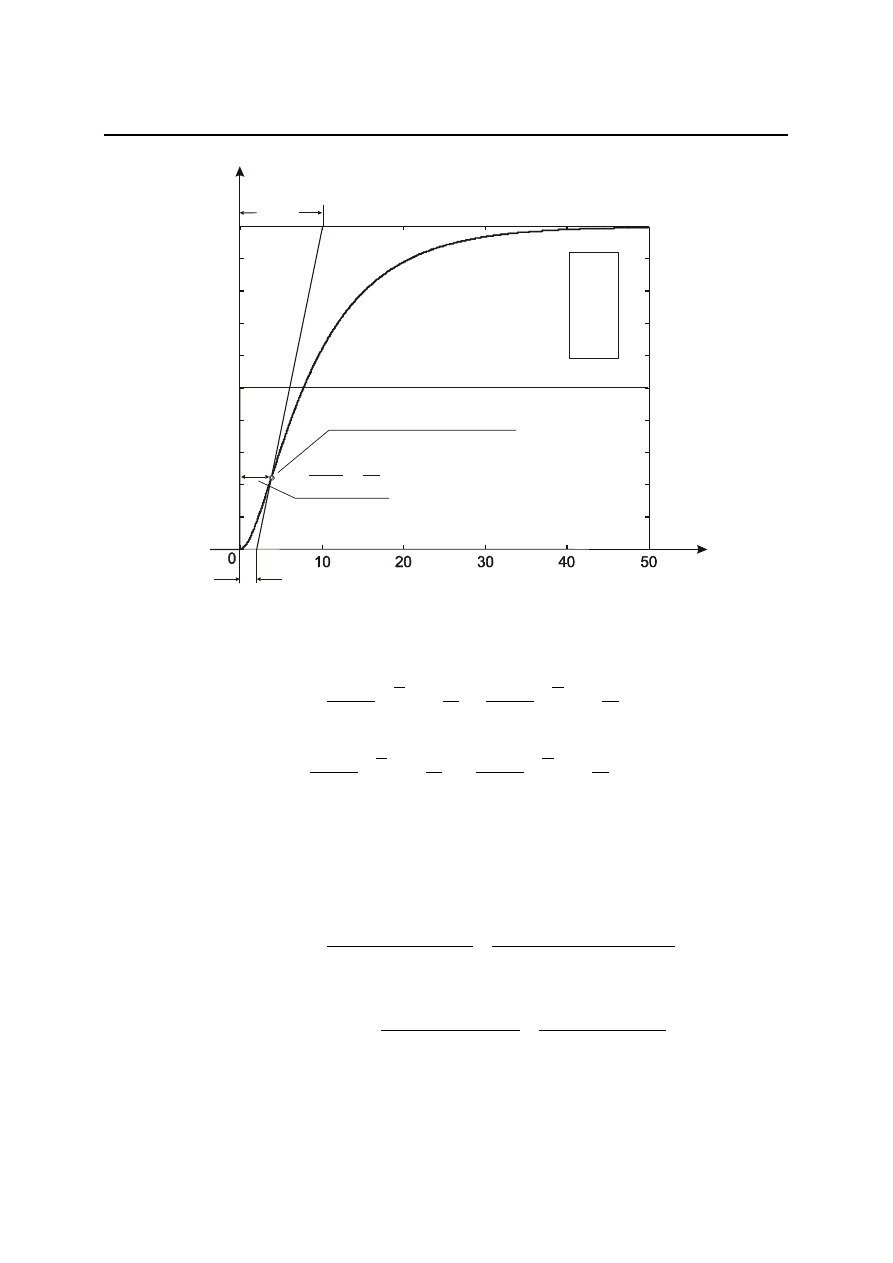
Przykładowy wykres charakterystyki skokowej elementu inercyjnego drugiego rzędu
przedstawiony jest na rys. 4.14.
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
84
Rys. 4.14. Odpowiedź jednostkowa członu inercyjnego drugiego rzędu
Punkt przegięcia charakterystyki skokowej określimy, przyrównując do zera drugą pochodną.
,
1
1
)
(
4
1
4
3
4
3
1
3
4
3
4
3
T
e
T
T
T
T
e
T
T
T
ka
t
h
t
T
t
T
0
1
1
)
(
2
4
1
4
3
4
2
3
1
3
4
3
4
3
T
e
T
T
T
T
e
T
T
T
ka
t
h
t
T
t
T
Stałe czasowe T
3
i T
4
można wyznaczyć graficznie z wykresu charakterystyki skokowej (rys.
4.14). Współczynnik wzmocnienia członu inercyjnego drugiego rzędu k określa się tak samo jak
członu inercyjnego (patrz rys. 4.4).
Charakterystykę amplitudowo-fazową oblicza się z relacji:
)
(
)
1
(
)
1
)(
1
(
)
(
4
3
4
3
2
4
3
T
T
j
T
T
k
T
j
T
j
k
j
G
(4.42)
lub
1
2
2
2
1
2
2
2
)
1
(
1
)
(
)
(
T
j
T
k
T
j
j
T
k
j
G
(4.43)
Przekształcając (4.42) wydzielimy część rzeczywistą P(
) i część urojoną Q(
) transmitancji
widmowej:
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
T
4
k=2
T =10
T =4
T =8
T =2
1
2
3
4
h(t)
t [sek]
T +T
3
4
T T
3
4
T -T
3
4
ln T
3
T
4
punkt przegięcia [h”(t)=0]
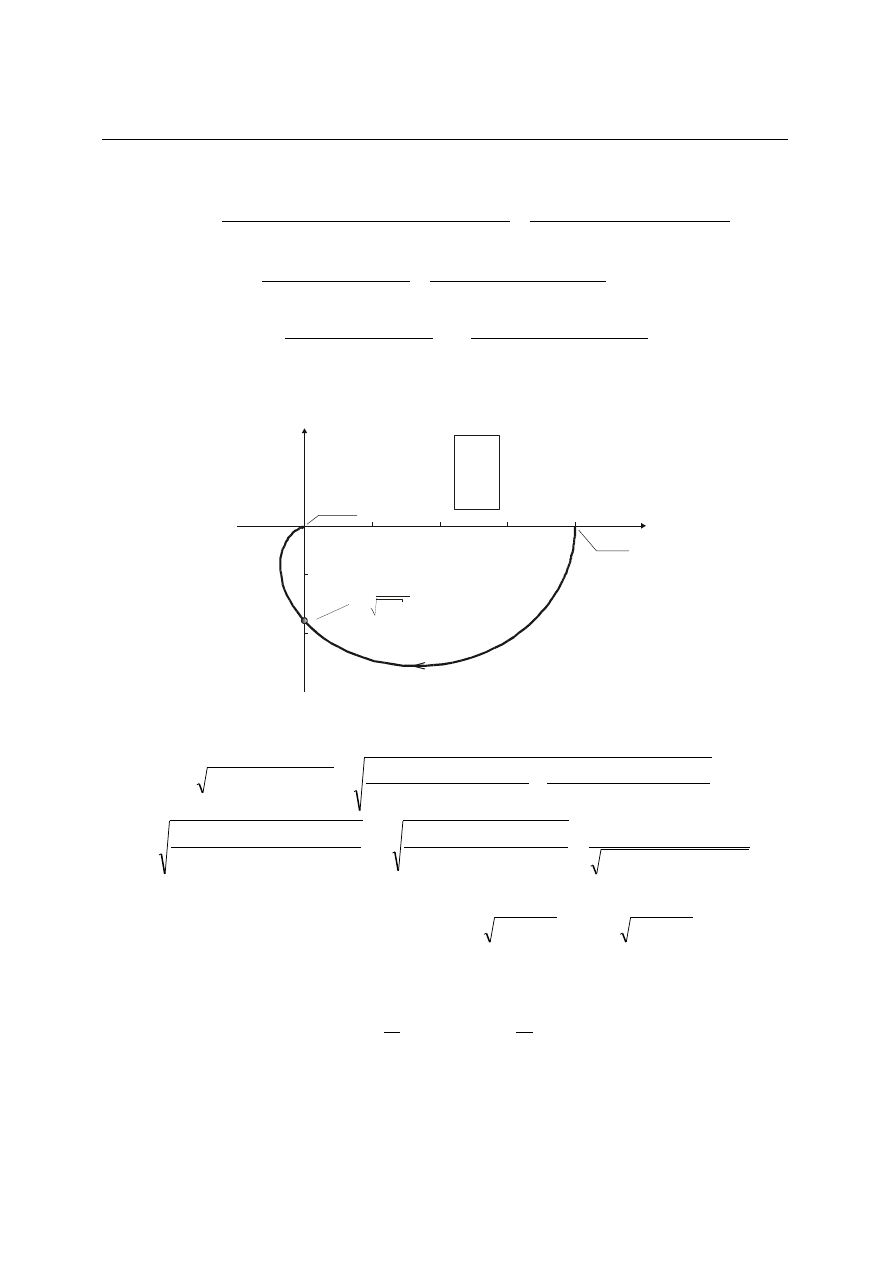
85
4. Podstawowe człony automatyki
;
)
1
)(
1
(
)
1
(
)
1
)(
1
)(
1
)(
1
(
)
1
)(
1
(
)
(
2
2
4
2
2
3
2
4
3
3
4
4
4
3
3
4
3
T
T
T
T
T
j
T
j
k
T
j
T
j
T
j
T
j
T
j
T
j
k
j
G
;
)
2
(
1
)
1
(
)
1
)(
1
(
)
1
(
)
(
4
2
4
2
2
2
1
2
2
2
2
2
2
4
2
2
3
2
4
3
T
T
T
T
k
T
T
T
T
k
P
(4.44)
.
)
2
(
1
)
1
)(
1
(
)
(
)
(
4
2
4
2
2
2
1
2
1
2
2
4
2
2
3
4
3
T
T
T
kT
j
T
T
T
T
k
j
Q
(4.45)
Wykres charakterystyki amplitudowo-fazowej członu inercyjnego drugiego rzędu przedstawiony
jest na rys. 4.15).
Rys. 4.15. Charakterystyka amplitudowo-fazowa elementu inercyjnego drugiego rzędu
Moduł charakterystyki częstotliwościowej:
.
)
1
)(
1
(
)
1
(
)
1
(
)
1
)(
1
(
)
1
)(
1
(
1
)
1
)(
1
(
)
(
)
1
)(
1
(
)
1
(
)
(
)
(
)
(
2
2
4
2
2
3
2
2
2
4
2
2
2
3
2
2
4
2
2
3
2
2
2
4
2
2
3
4
2
4
2
3
2
2
4
2
2
3
2
2
2
4
2
2
3
2
2
1
2
2
2
2
2
4
2
2
3
2
2
4
3
2
2
2
T
T
k
T
T
T
T
k
T
T
T
T
T
T
k
T
T
T
T
k
T
T
T
T
k
Q
P
M
Logarytmiczną charakterystykę amplitudową oblicza się z relacji:
2
2
4
2
2
3
1
log
20
1
log
20
log
20
)
(
log
20
)
(
T
T
k
M
L
(4.46)
Charakterystyka ta może być aproksymowana trzema odcinkami prostych. Ma dwie pulsacje
załamania (rys. 4.16):
3
1
1
T
oraz
.
1
4
2
T
Dla pulsacji
1
zależność (4.46) może być zastąpiona wyrażeniem przybliżonym:
,
log
20
)
(
k
L
0.5
1
1.5
2
-1.5
-1
-0.5
0
P( )
Q( )
h
k = 2
T = 10
T = 4
T = 8
T = 2
1
2
3
4
1
T T
3 4
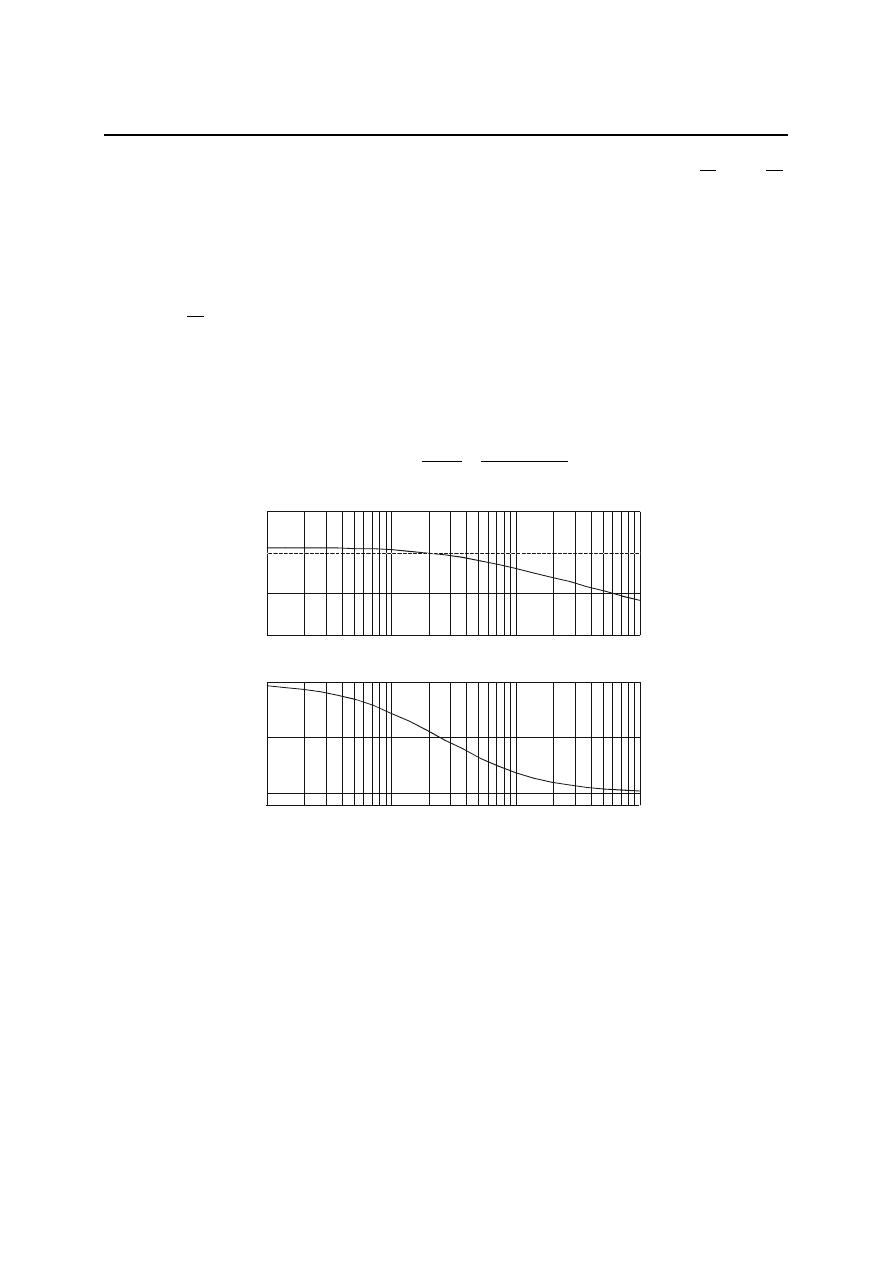
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
86
co odpowiada prostej poziomej wyrażającej wzmocnienie k. Następnie dla pulsacji
4
3
1
1
T
T
charakterystyka amplitudowa może być aproksymowana wyrażeniem przybliżonym:
3
log
20
log
20
)
(
T
k
L
Jest to prosta o nachyleniu –20 dB/dek.
Dla
4
1
T
przybliżone wyrażenie tej charakterystyki będzie miało postać:
.
log
20
log
20
log
20
)
(
4
3
T
T
k
L
Temu równaniu odpowiada prosta o nachyleniu –40 dB/dek.
Charakterystykę fazową członu dwuinercyjnego określa wzór:
2
4
3
4
3
1
)
(
)
(
)
(
tg
)
(
T
T
T
T
P
Q
arc
Rys. 4.16. Charakterystyki logarytmiczne członu inercyjnego drugiego rzędu
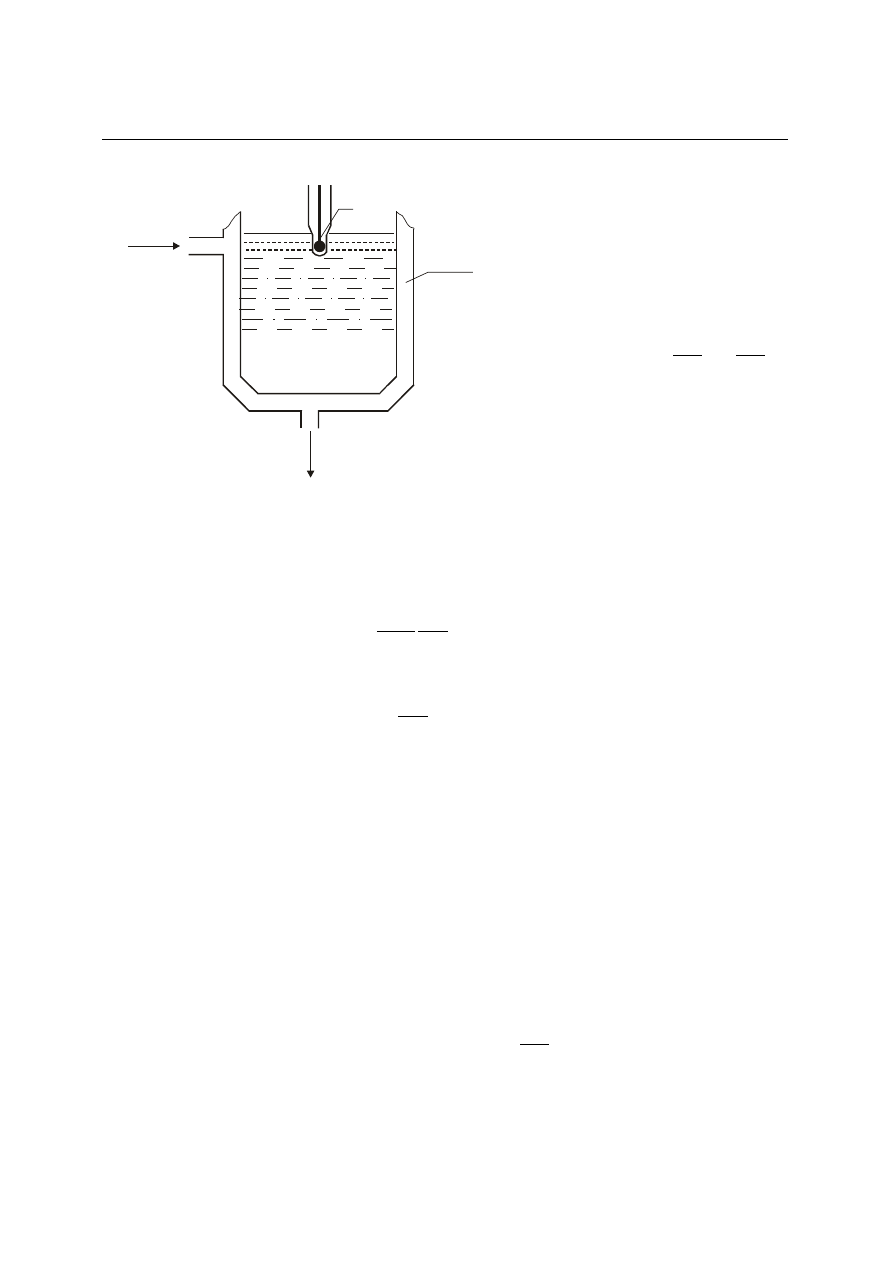
Przykład członu inercyjnego drugiego rzędu
Jako przykład członu inercyjnego drugiego rzędu rozpatrzymy ogrzewany zbiornik i zanurzony
w cieczy znajdującej się w tym zbiorniku termometr rtęciowy (rys. 4.17). Bańka termometryczna
może być uważana za układ pierwszego rzędu, który można opisać liniowym równaniem
różniczkowym pierwszego rzędu. Wyprowadzimy to równanie przy następujących założeniach:
- rozpatrujemy termometr rtęciowy, zanurzony gwałtownie w cieczy o temperaturze
1
;
- pojemność cieplną szkła pomijamy;
- rtęć ma jednakową temperaturę
2
.
10
10
-2
-2
10
10
-1
-1
10
10
0
0
10
10
1
1
-100
-50
0
0
50
Frequency (rad/sec)
Frequency (rad/sec)
-90
-180
87
4. Podstawowe człony automatyki
Ogólna postać równania cieplnego stanu
nieustalonego takiego układu:
natężenie dopływu ciepła - natężenie
odpływu ciepła = zmiana energii
wewnętrznej
a więc dla termometru:
dt
d
C
dt
d
Mc
A
pr
2
2
2
1
0
)
(
gdzie : M - masa rtęci;
c
pr
- ciepło właściwe rtęci;
α - ogólny współczynnik
przenikania ciepła;
A - powierzchnia przenikania
ciepła;
t - czas.
Równanie cieplne przyjmuje zatem jedną z poniższych form:
1
2
2
dt
d
A
Mc
pr
lub
.
1
2
2
dt
d
T
Wyrażenie Mc
pr
/αA ma wymiar czasu i nazywa się stałą czasową T układu. Wielkość T jest
miarą czasu potrzebnego dla dopasowania się układu do nowej wartości wejściowej.
Analogicznie do układów elektrycznych, w których stała czasowa jest iloczynem rezystancji i
pojemności elektrycznej RC , stała czasowa termometru jest iloczynem oporności cieplnej 1/αA i
pojemności cieplnej Mc
p
.
Jeśli układ można potraktować jako układ pierwszego rzędu, stałą czasową otrzymuje się
bezpośrednio z wartości oporu i współczynnika pojemności układu, bez potrzeby układania
równania bilansu materiałowego.
Analogiczne rozumowanie dotyczące zbiornika pozwoli zapisać równanie cieplne zbiornika w
postaci
dt
d
c
M
A
pc
c
p
1
1
1
1
)
(
gdzie: M
c
- masa cieczy w zbiorniku;
c
pc
- ciepło właściwe cieczy.
odpływ
pary
płaszcz
wodny
para
grzejna
p
Rys. 4.17. Układ zbiornik-termometr rtęciowy jako
przykład członu dwuinercyjnego

Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
88
Podstawiając do tego równania
1
wyliczone z równania dla termometru otrzymamy
p
R
R
dt
d
T
T
dt
d
TT
2
2
2
2
2
)
(
gdzie:
.
,
1
1
R
pr
pc
c
T
A
Mc
T
A
c
M
4.3. Człony całkujące
Ogólna postać równania różniczkowego idealnego członu całkującego jest następująca:
dy
dt
kx
(4.47)
Postać całkowa, przy zerowych warunkach początkowych
t
xdt
k
y
0
(4.48)
skąd wynika transmitancja
G s
y s
x s
k
s
( )
( )
( )
(4.49)
Współczynnik k definiuje się jako
k
dy
dt
x
.
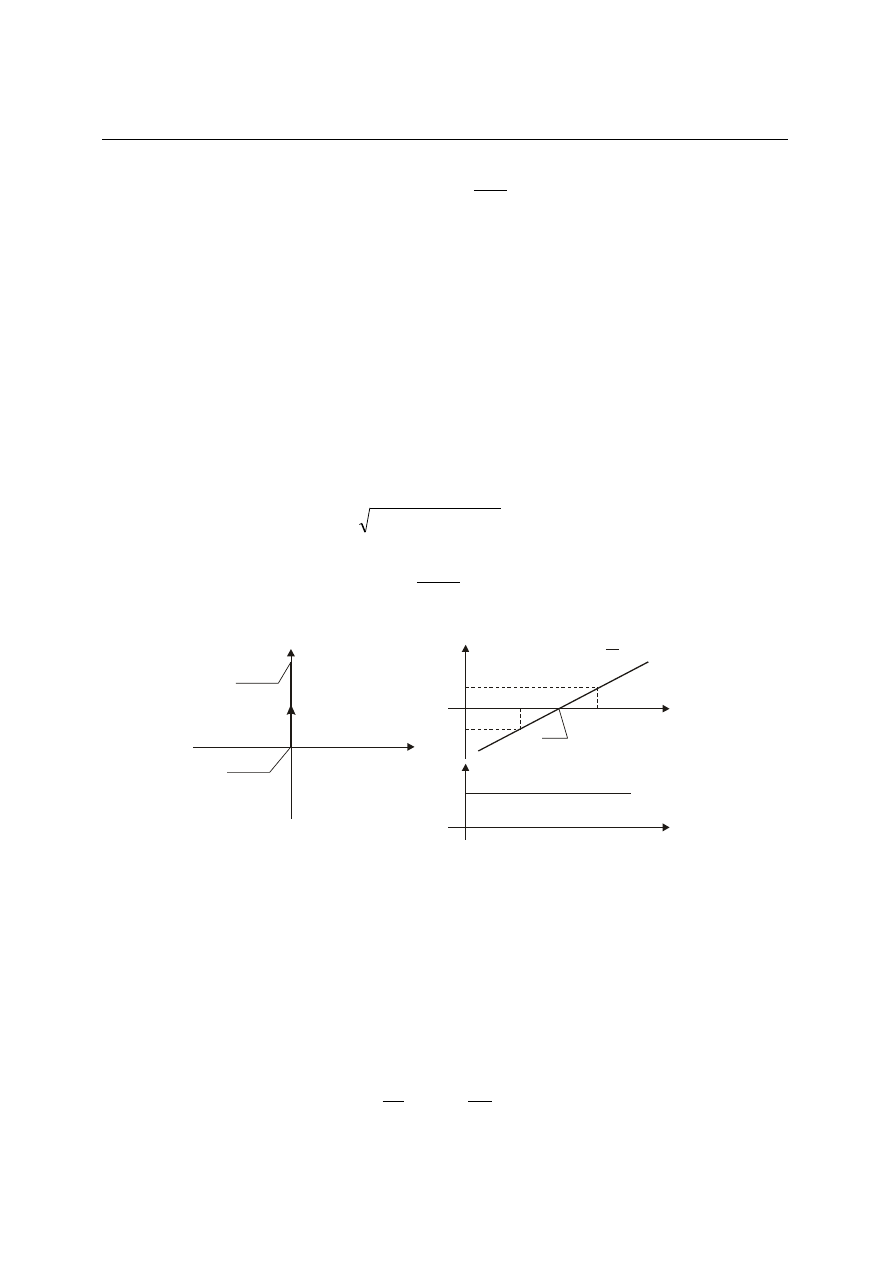
Równanie charakterystyki statycznej wynika z (4.47) i ma postać
x
0,
a jej wykres podano na rys. 4.18a. Pewna analiza tego wykresu zamieszczona została w opisie
przykładu członu całkującego.
Rys. 4.18. Charakterystyka statyczna członu całkującego: a) współrzędne odchyłek, b)
współrzędne wartości absolutnych (patrz przykład)
Odpowiedź na wymuszenie skokowe
a
t
t
x
)
(
1
)
(
wyznaczamy z definicji:
y
x
a)
y
0
x
0
x
n
0
b)
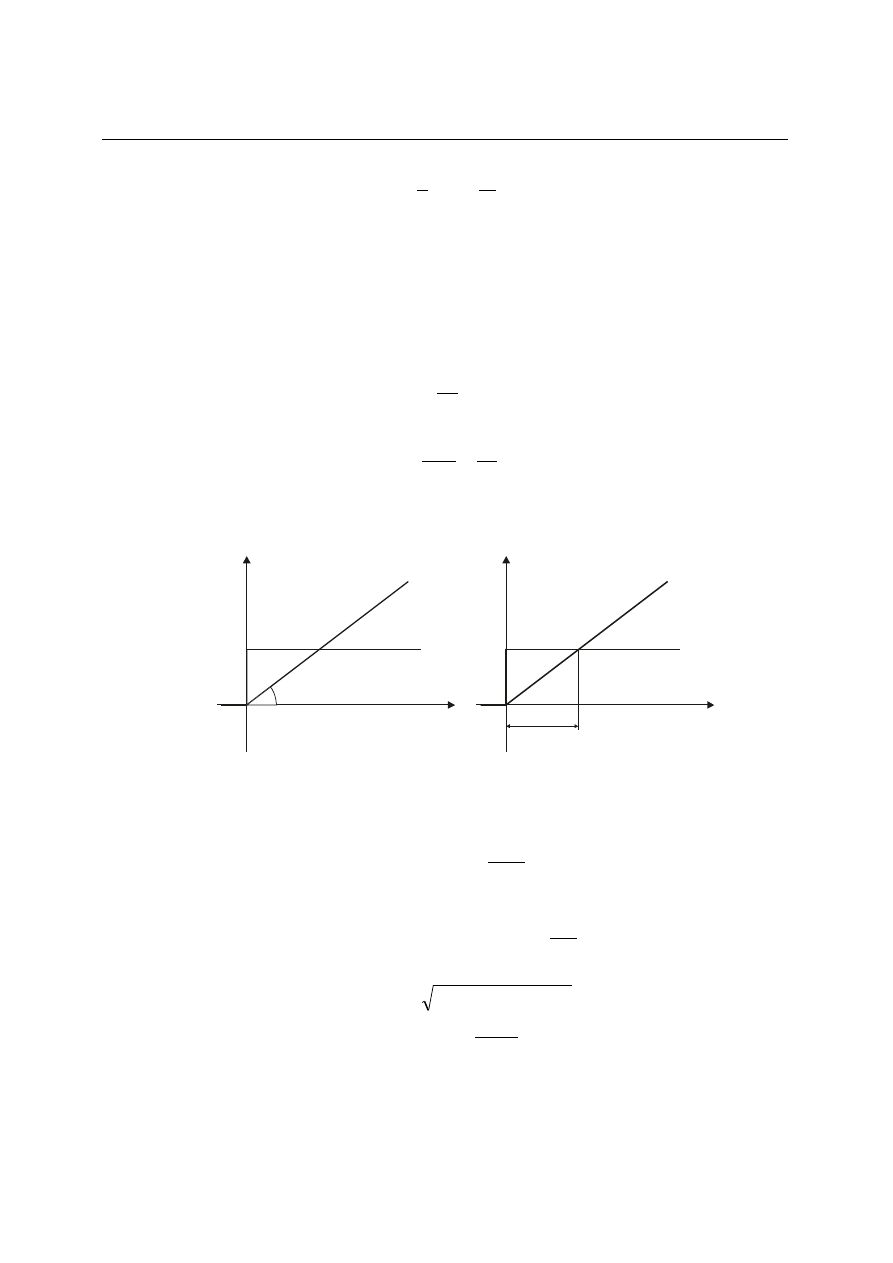
89
4. Podstawowe człony automatyki
.
)]
(
[
)
(
,
)
(
)
(
1
2
t
a
k
s
y
L
t
h
a
s
k
s
x
s
k
s
h
(4.50)
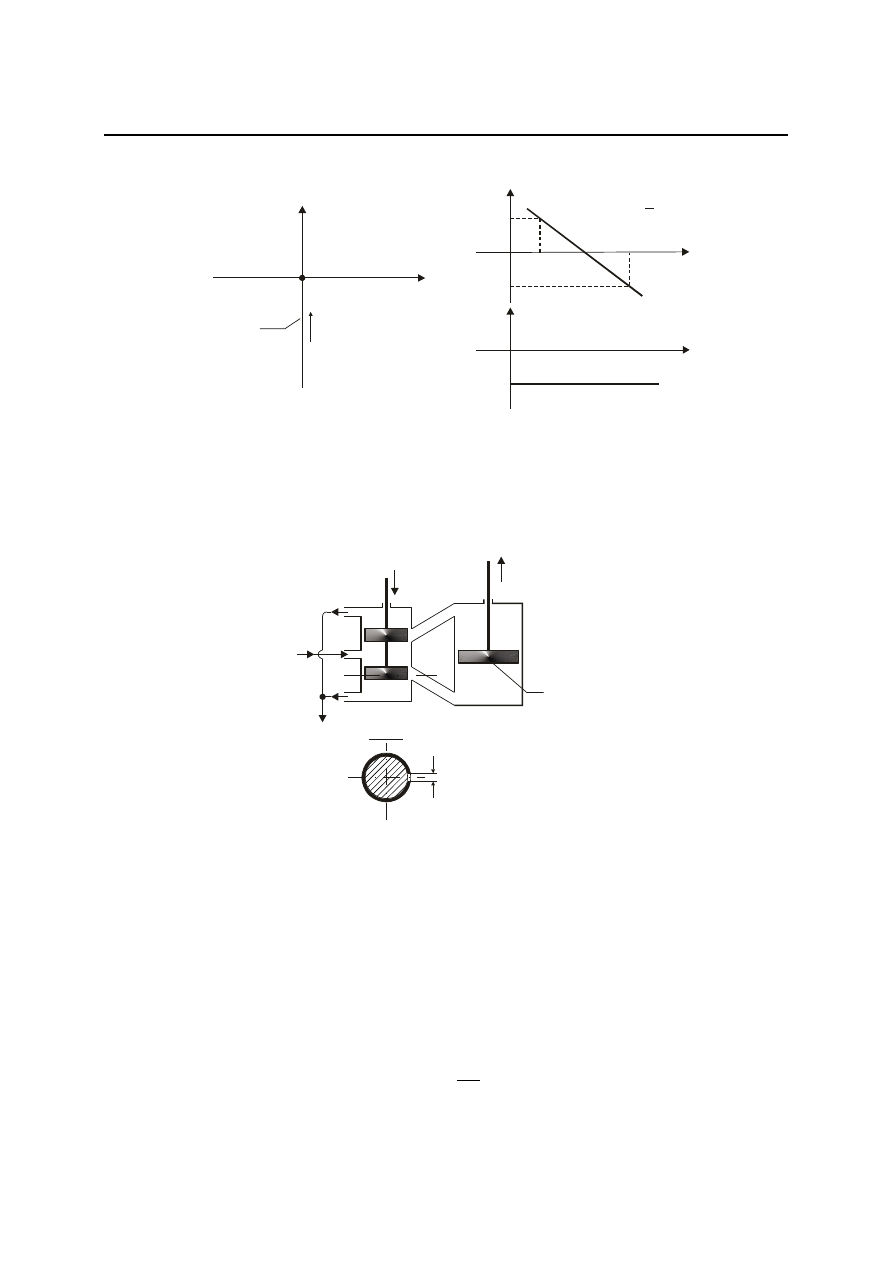
Wykres h(t) członu idealnie całkującego przedstawiony jest na rys. 4.19
W przypadku szczególnym kiedy wejście i wyjście są sygnałami jednoimiennymi,
współczynnik k ma wymiar odwrotności czasu. Równanie (4.47) przedstawia się wówczas w
postaci
T
dy
dt
x
,
(4.51)
której odpowiada transmitancja
G s
y s
x s
Ts
( )
( )
( )
,
1
(4.52)
gdzie T jest stałą czasową akcji całkującej lub krócej - stałą całkowania. Stałą tą można odszukać
na wykresie odpowiedzi skokowej zgodnie z rys. 4.19b.
Rys. 4.19. Odpowiedzi skokowe członu całkującego: a) G(s)=k/s, b) G(s)=1/Ts
Transmitancję widmową elementu całkującego wyznaczymy na podstawie transmitancji
operatorowej (4.52)
.
1
)
(
jT
j
G
(4.53)
Części rzeczywista i urojona
)
(
j
G
są równe:
P
Q
T
( )
,
( )
.
0
1
(4.54)
Logarytmiczne charakterystyki amplitudowa i fazowa:
L
P
Q
T
( )
log [ ( )]
[ ( )]
log
,
20
20
2
2
(4.55)
( )
( )
( )
(
)
.
arc tg
Q
P
arctg
90
o
(4.56)
y
y
x
x
a)
b)
t
t
a
a
arc tg ka
T
y(t)
y(t)
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
90
Wykresy
G j
L
i
(
), ( ) ( )
podano na rys. 4.20.
Rys. 4. 20. Charakterystyki idealnego członu całkującego: a) charakterystyka
amplitudowo-fazowa, b) logarytmiczne charakterystyki amplitudowa i fazowa
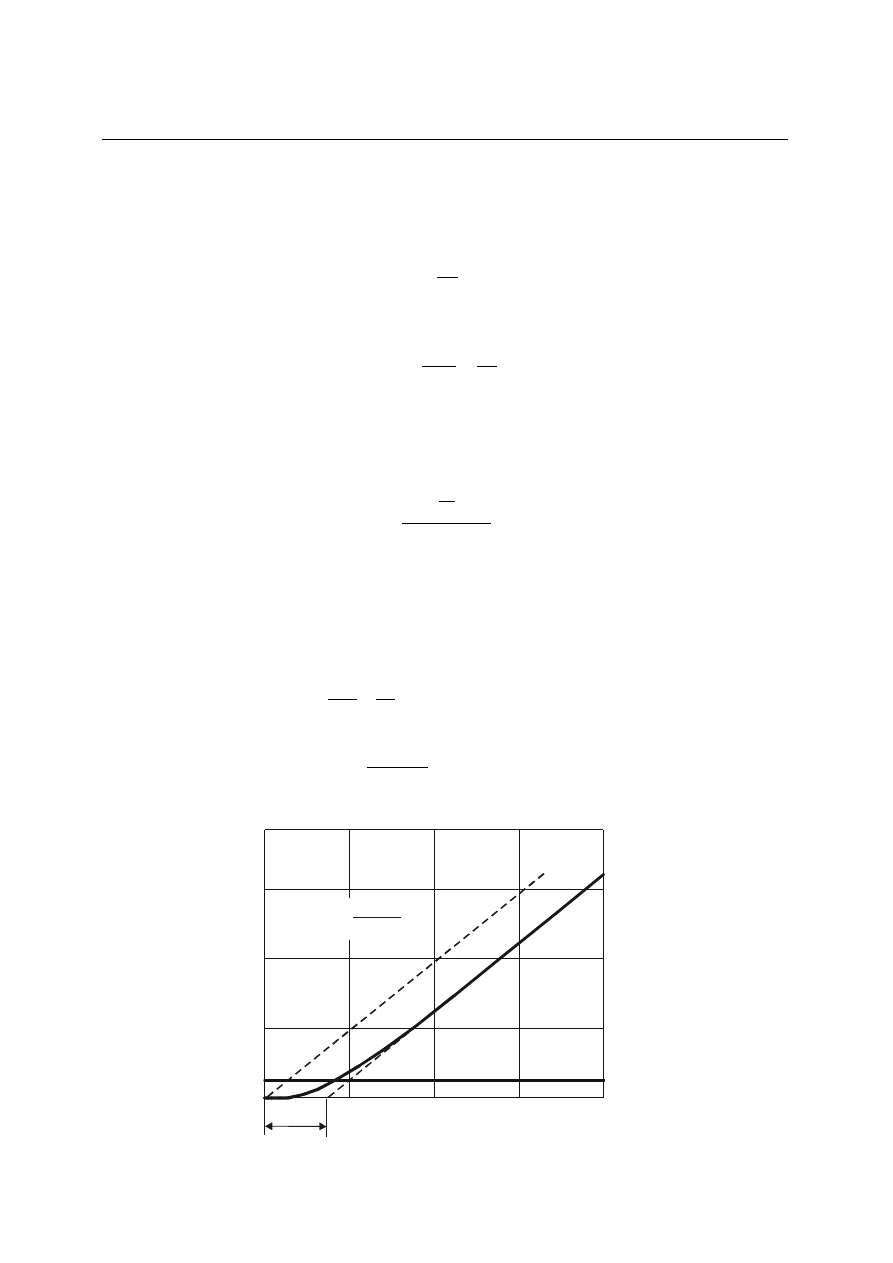
Przykład . Zespół rozdzielacz - siłownik hydrauliczny
Schemat elementu przedstawiono na rys. 4.21 Wielkością wejściową jest przesunięcie x
tłoczków rozdzielacza, wielkością wyjściową jest przesunięcie y tłoczyska siłownika.
Rys. 4.21. Zespół rozdzielacz-siłownik hydrauliczny
Założenia:
a) p
z
= const, p
s
= const.
b) obciążenie siłownika ma wartość zerową,
c) prędkość przepływu oleju przez szczeliny rozdzielacza v = const (wynika to z założeń a
i b).
Stan ustalony y = const zachodzi dla x = 0. Charakterystyka statyczna ma kształt podany
na rys. 4.18.
Stan dynamiczny opisuje zależność:
Q
A
dy
dx
,
gdzie Q - natężenie przepływu oleju przez szczeliny rozdzielacza, A - powierzchnia efektywna
a)
b)
jQ( )
P( )
G(j )
h
L( )
dB
20
-20
-20dB/dek
s
s
s
0.1
10
s
T
1
=
-90
o
b
A
y
x
p
z
p
s
I
I
I - I
91
4. Podstawowe człony automatyki
tłoka siłownika.
Uwzględniając równanie ciągłości
Q xbv
(xb jest przekrojem szczeliny przepływowej) otrzymamy
T
dy
dt
x
,
(4.57)
gdzie T = A/bv.
Transmitancja elementu:
G s
y s
x s
Ts
( )
( )
( )
.
1
(4.58)
Jeżeli siłownik zostanie obciążony siłą F, stałą co do wielkości i kierunku, to rozważany
element przestanie być liniowy, gdyż wartość stałej czasowej T zależeć będzie od kierunku
przesunięć. Przy przesunięciach tłoka zgodnych z kierunkiem działania siły F, spadki ciśnienia w
szczelinach rozdzielacza wyniosą
p
F
A
p
z
s
2
(wtedy v = c
1
i T = T
2
).
Często spotyka się człony całkujące nie idealne. Rozpatrzymy dwa takie przypadki.
Człon całkujący z opóźnieniem (człon całkujący rzeczywisty) opisuje równanie
różniczkowe
x
k
dt
dy
dt
y
d
T
2
2
(4.59)
Jego transmitancja operatorowa ma postać
)
1
(
)
(
Ts
s
k
s
G
(4.60)
zaś wzór na charakterystykę skokową znajdziemy w tablicy przekształceń Laplace’a
h(t)
t[sek]
1(t)
G(s)=
k
s(1+Ts)
k=1
T=3
5
10
15
0
5
10
15
T
kt
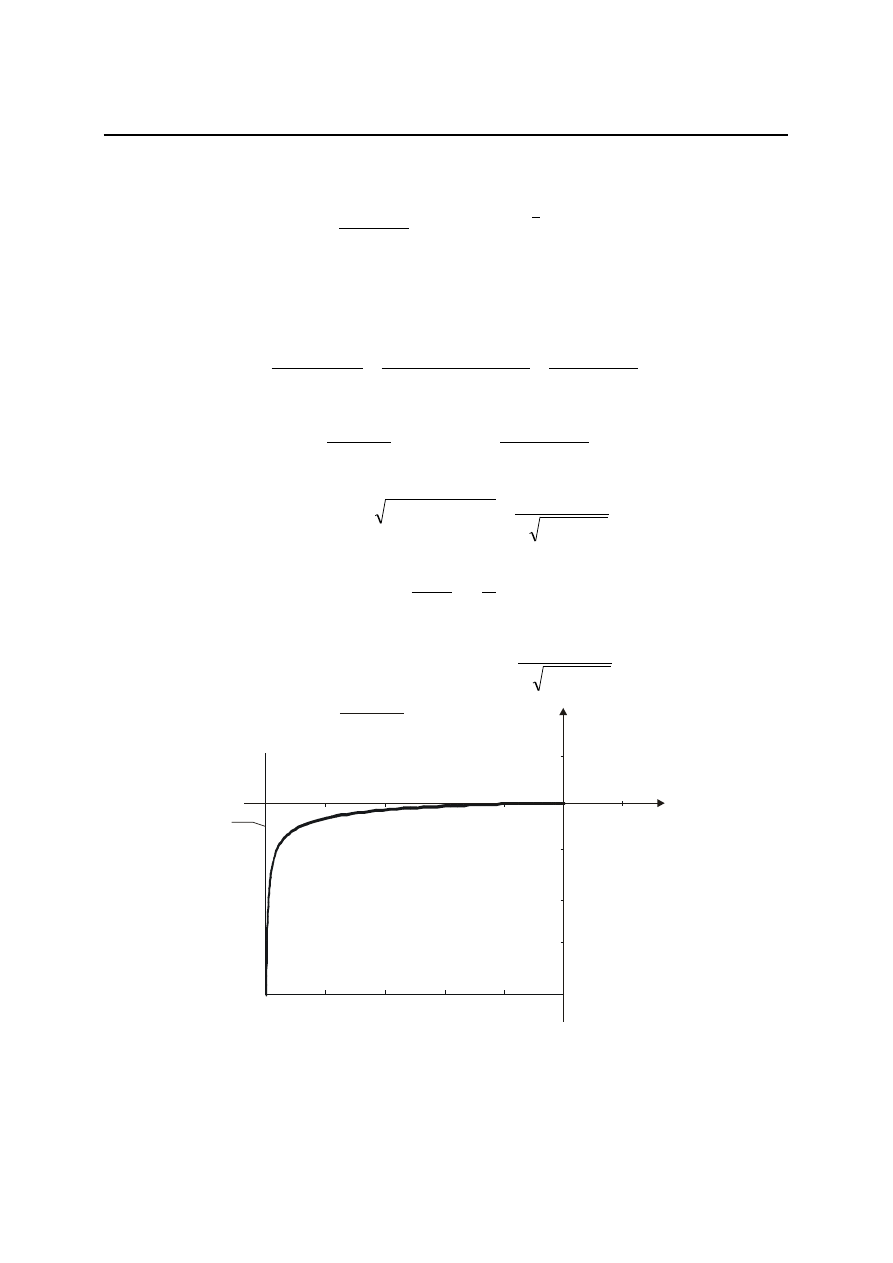
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
92
Rys. 4.22. Charakterystyka skokowa członu całkującego z opóźnieniem
)
1
(
)
1
(
)
(
2
1
T
t
e
T
t
k
Ts
s
k
t
h
L
(4.61)
Wykres tej charakterystyki przedstawiony jest na rys. 4.22.
Charakterystyki częstotliwościowe można wyrazić następująco:
transmitancja widmowa
)
1
(
)
1
)(
1
(
)
1
(
)
1
(
)
(
2
2
T
kT
jk
T
j
T
j
T
j
jk
jT
j
k
j
G
(4.62)
części rzeczywista i urojona
G j
(
):
)
1
(
)
(
,
1
)
(
2
2
2
2
T
k
j
Q
T
kT
P
(4.63)
moduł M(
)
,
)
(
1
)
(
)
(
)
(
2
2
2
T
k
Q
P
M
(4.64)
logarytmiczna charakterystyka fazowa
,
)
tg(
2
)
(
)
(
tg
)
(
T
arc
P
Q
arc
(4.65)
zaś logarytmiczna charakterystyka amplitudowa L(
)
.
)
(
1
log
20
)
(
log
20
)
(
2
T
k
M
L
(4.66)
-10
-8
-6
-4
-2
2
-200
-150
-100
-50
0
50
Q(
)
P(
)
G(s)=
s(Ts+1)
k
k=2, T=5
-kT
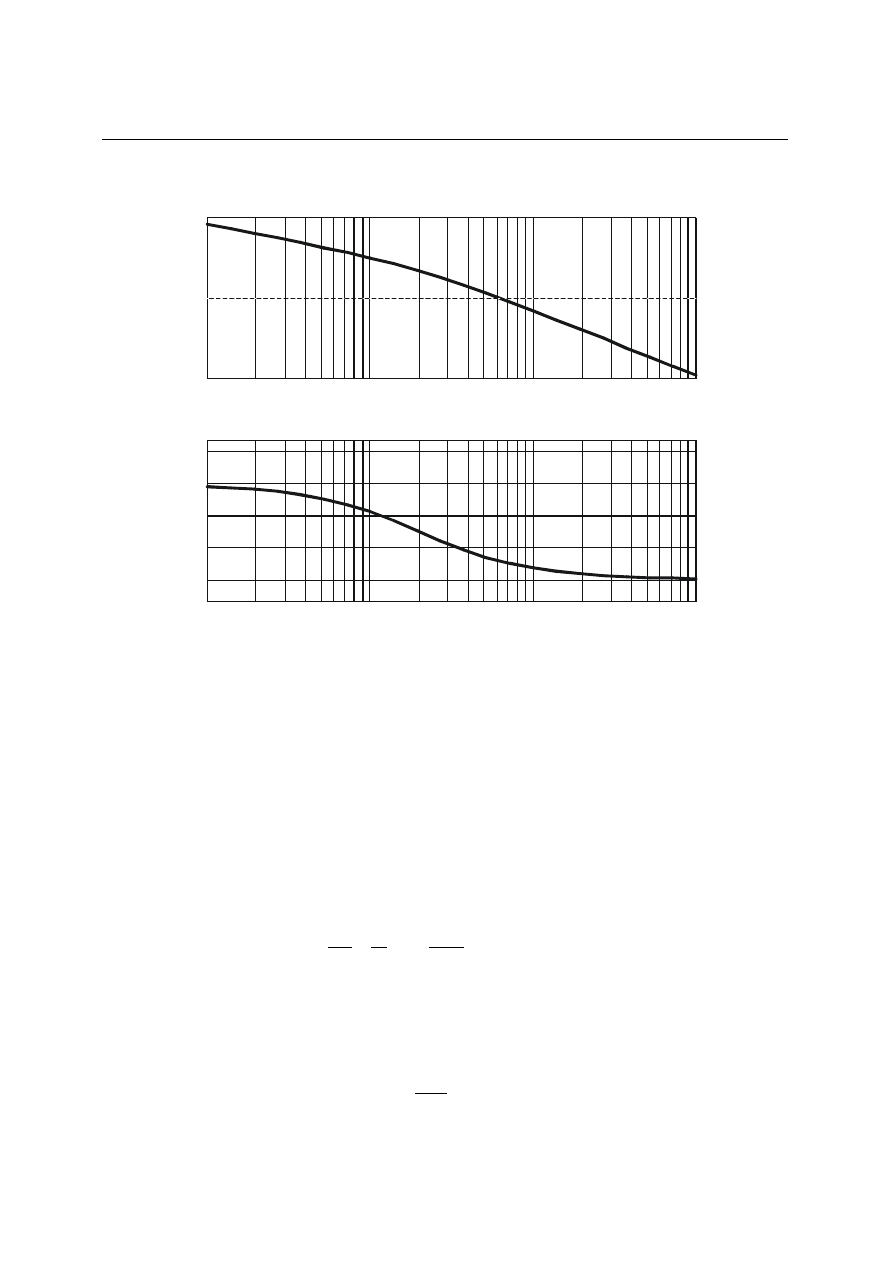
Przykładowe charakterystyki częstotliwościowe członu całkującego rzeczywistego przedstawione
są na rys. 4.23 i 4.24.
Rys. 4.23. Charakterystyka amplitudowo-fazowa członu całkującego rzeczywistego
93
4. Podstawowe człony automatyki
10
-2
-2
10
10
-1
-1
10
10
0
0
10
10
1
1
-50
0
50
-6
0
-9
0
-1
2
0
-1
5
0
-1
8
0
L
(
)
[d
B
]
o
rad/sek]
rad/sek]
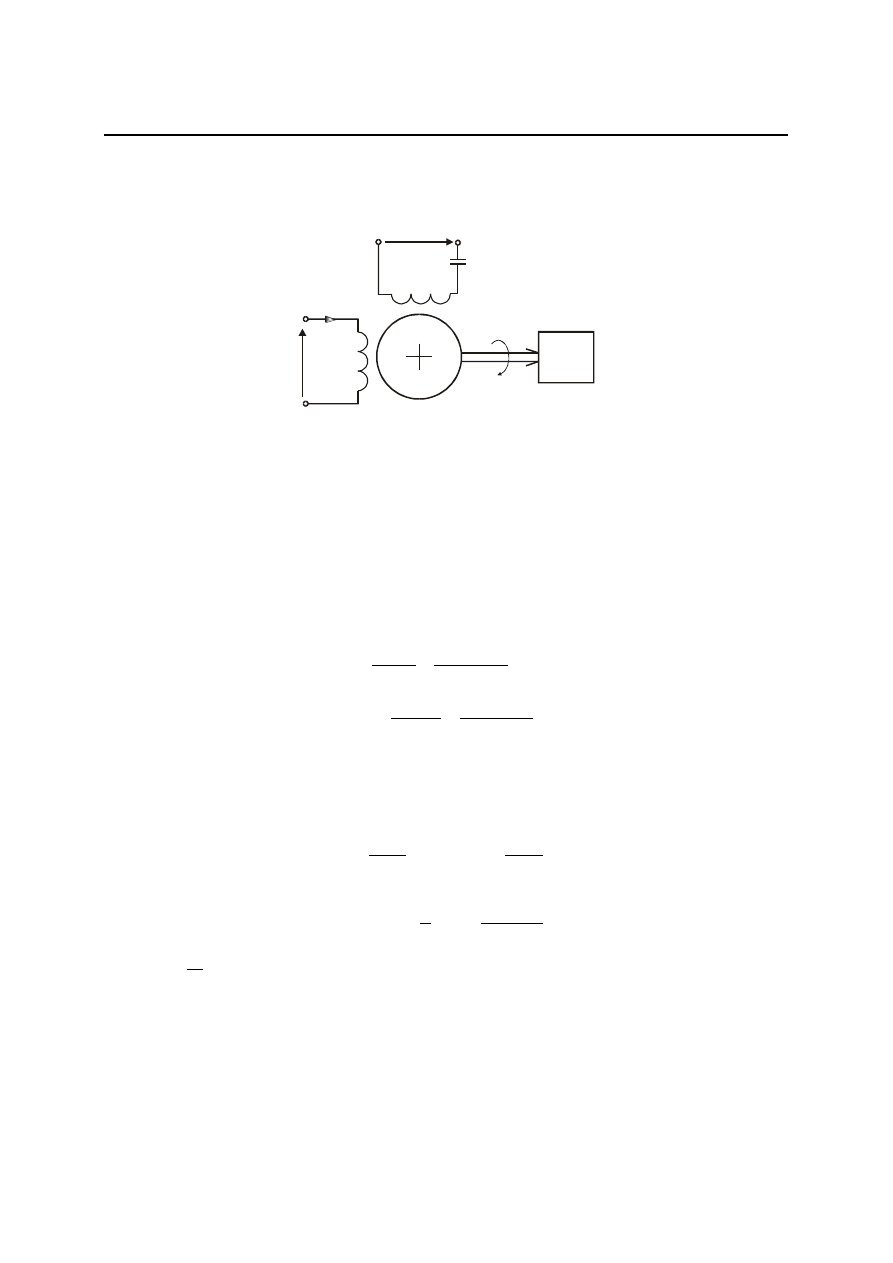
Rys. 4.24. Charakterystyki logarytmiczne członu całkującego rzeczywistego
Przykład. Silnik dwufazowy asynchroniczny
Dwufazowe silniki asynchroniczne często wykorzystuje się w UAR. Najczęściej znajdują
zastosowanie w układach śledzących małej mocy. Wykonywane są zazwyczaj w dwóch wersjach:
z kubkowym, zazwyczaj aluminiowym wirnikiem oraz z ferromagnetycznym wirnikiem,
posiadającym krótko zwarte uzwojenie. Pierwszy typ silnika ma co prawda mniejszą sprawność
energetyczną, jednak mała bezwładność i lepsze parametry regulacji prędkości obrotowej
preferują jego stosowanie. Moc omawianych silników nie przekracza 100
200 W. Schemat
elektryczny
silnika dwufazowego przedstawiony jest na rys. 4.25.
Zakładając stałą amplitudę napięcia wzbudzenia można napisać
,
1
1
M
c
c
U
c
dt
d
M
e
x
e
(4.67)
gdzie:
s
dt
d
/
- prędkość obrotowa silnika, [rad/s];
- kąt obrotu wału silnika, [rad]; U
x
–
wartość skuteczna napięcia na uzwojeniu sterującym silnika, [V]; M – moment napędowy silnika,
[Nm]; c
e
, c
M
– współczynniki stałe silnika, [V
s/rad]; [N
m/V].
Równocześnie możemy napisać równanie momentów
st
M
dt
d
I
M
2
2
(4.68)
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
94
gdzie: I – moment bezwładności, [kg
m
2
]; M
st
– statyczny moment oporu.
Rys. 4.25. Asynchroniczny silnik dwufazowy jako przykład członu całkującego z inercją
Łącząc równania (4.67), (4.68) możemy zapisać ostateczne równanie silnika
dwufazowego w postaci operatorowej
,
)
(
)
(
)
(
)
1
(
s
M
k
s
U
k
s
s
s
T
st
em
x
s
em
(4.69)
gdzie: k
s
=1/c
e
, k
em
=1/c
e
c
M
– współczynniki silnika odpowiadające torowi sterowania i torowi
zakłóceń; T
em
= I/(c
e
c
M
) – elektromechaniczna stała czasowa, [s];
Transmitancja przejścia silnika przyjmie postać:
zaklócenia
tor
s
T
s
k
s
M
s
s
G
sterowania
tor
s
T
s
k
s
U
s
s
G
em
em
st
zak
s
em
s
x
s
)
1
(
)
(
)
(
)
(
)
1
(
)
(
)
(
)
(
.
(4.70)
Człon izodromowy
Członem izodromowym nazywamy człon automatyki, dla którego równanie opisujące
dynamikę ma postać:
dt
t
dx
k
t
x
k
dt
t
dy
)
(
)
(
)
(
1
(4.71)
Transmitancja operatorowa wyraża się wzorem
s
Ts
k
k
s
k
s
G
)
1
(
)
(
1
(4.72)
gdzie:
k
k
T
1
- stała czasowa członu izodromowego.
Z przedstawionych zależności wynika, że omawiany człon można przedstawić jako sumę
działania dwóch członów (połączenie równoległe): idealnego całkującego ze współczynnikiem k i
proporcjonalnego o współczynniku proporcjonalności k
1
.
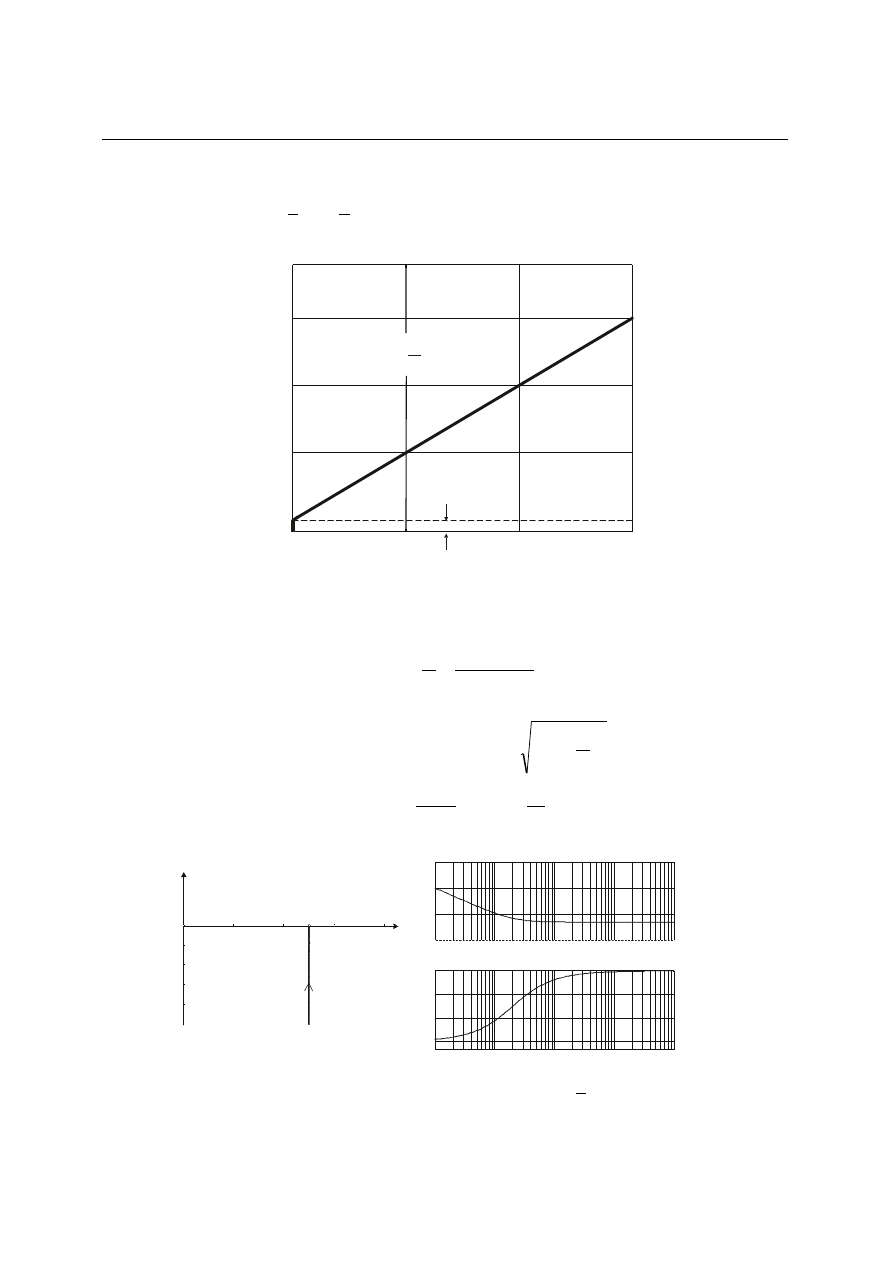
Charakterystyka skokowa będzie sumą charakterystyk skokowych członu
proporcjonalnego i całkującego idealnego
U = const
w
uzwojenie
wzbudzenia
uzwojenie
sterujące
U
x
C
w
M
95
4. Podstawowe człony automatyki
a
t
k
k
a
s
k
k
s
L
t
h
)
(
1
)
(
1
1
1
(4.73)
Wykres tej charakterystyki przedstawiony jest na rys. 4.26.
Rys. 4.26. Charakterystyka skokowa członu izodromowego
Transmitancja widmowa ma postać
j
T
j
k
k
j
k
j
G
)
1
(
)
(
1
(4.74)
a charakterystyki logarytmiczne liczy się ze wzorów
2
2
1
log
20
)
(
log
20
)
(
k
k
M
L
(4.75)
1
tg
)
(
)
(
tg
)
(
k
k
arc
P
Q
arc
(4.76)
Wykresy tych charakterystyk przedstawione są na rys. 4.27.
10
10
-2
-2
10
10
-1
-1
10
10
0
0
10
10
1
1
10
10
2
2
0
20
40
60
-30
-60
-90
0
2
4
6
8
-100
-80
-60
-40
-20
0
Q( )
P( )
a)
b)
k=1
k =5
1
[
]
rad/sek
[
]
rad/sek
L(
[d
B
]
[
]
o
Rys. 4.27. Charakterystyki członu izodromowego
5
1
)
(
s
s
G
: a) charakterystyka a-f,
0
5
10
15
5
10
15
20
k
1
h(t)
G(s)= ks +k
1
k =5
1
k=1
Czas [s]
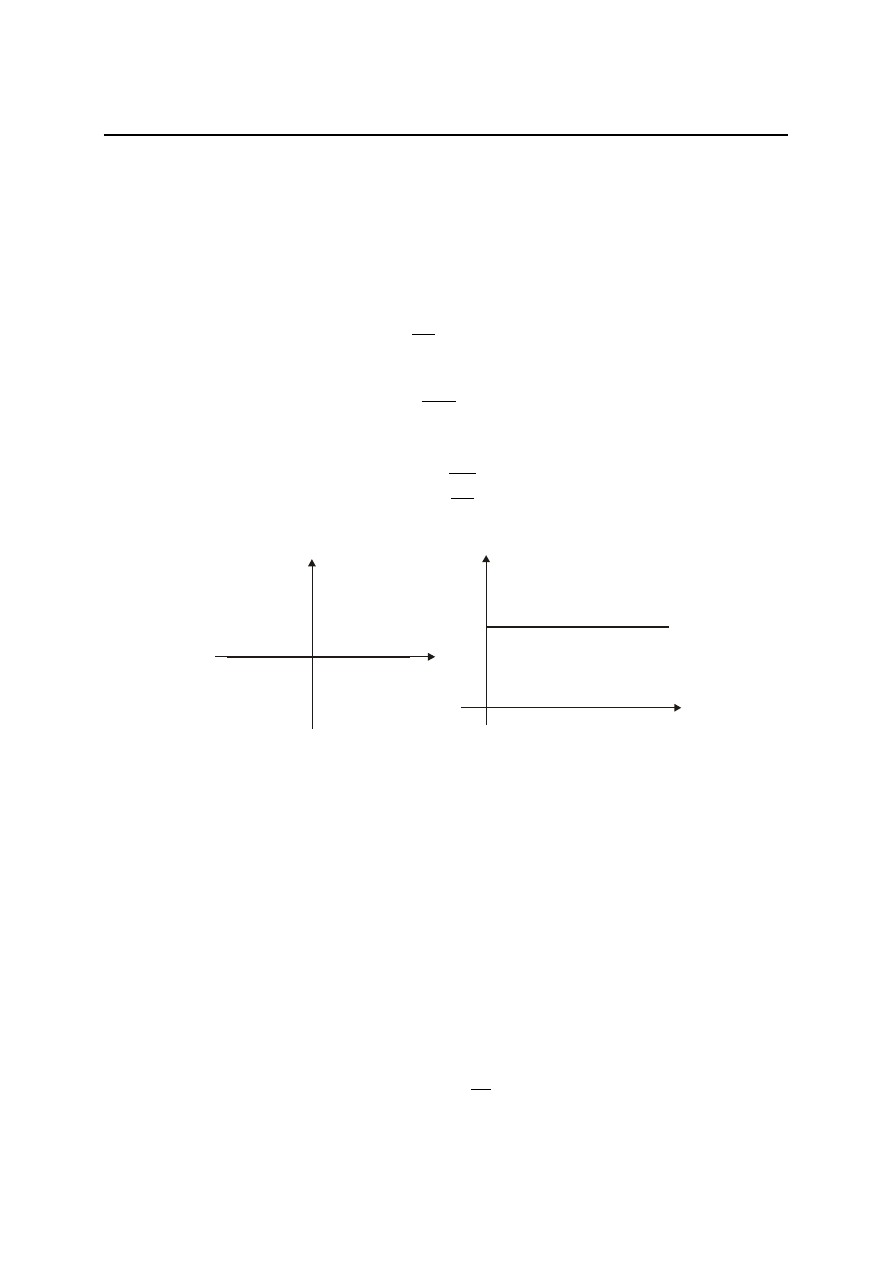
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
96
b) logarytmiczne amplitudowa i fazowa
4.4. Elementy różniczkujące
Idealny element różniczkujący
Równanie idealnego elementu różniczkującego jest następujące:
y k
dx
dt
,
(4.77)
skąd wynika transmitancja
G s
y s
x s
ks
( )
( )
( )
.
(4.78)
Współczynnik k definiuje się jako:
k
y
dx
dt
W stanie ustalonym y = 0 (y
0
= const) dla wszystkich x. Wykresy charakterystyki
statycznej podano na rys. 4.28.
Rys. 4.28. Charakterystyka statyczna członu różniczkującego idealnego: a) współrzędne
odchyłek, b) współrzędne wartości absolutnych
Odpowiedź na wymuszenie skokowe
a
t
t
x
)
(
1
)
(
jest funkcją Diraca pomnożoną przez k
oraz przez amplitudę skoku a. Mamy bowiem
.
)
(
)
(
ka
s
x
s
k
s
y
Na podstawie tablicy przekształceń Laplace’a
,
)
(
)]
(
[
)
(
1
t
a
k
s
y
L
t
y
(4.79)
a zatem
.
0
0
,
0
,
0
0
)
(
t
dla
t
dla
t
dla
t
y
(4.80)
W przypadku szczególnym, kiedy wejście i wyjście są sygnałami jednoimiennymi,
równanie (4.77) zapisuje się w postaci
,
dt
dx
T
y
D
(4.81)
której odpowiada transmitancja
y
x
a)
y
0
y
n
x
0
b)
0
97
4. Podstawowe człony automatyki
,
)
(
)
(
)
(
s
T
s
x
s
y
s
G
D
(4.82)
gdzie T
D
jest stałą czasową akcji różniczkującej lub krócej - stałą różniczkowania.
Odpowiedź na wymuszenie skokowe jest w tym przypadku funkcją Diraca pomnożoną
przez T
D
a, a zatem jest również opisana przez (4.80).
Transmitancja widmowa idealnego elementu różniczkującego, wyznaczona na podstawie
transmitancji operatorowej (4.82) jest następująca:
.
)
(
D
jT
j
G
(4.83)
Części rzeczywista i urojona
G j
(
)
:
.
)
(
,
0
)
(
D
T
Q
P
(4.84)
Logarytmiczne charakterystyki amplitudowa i fazowa mają postać:
,
log
20
)]
(
[
)]
(
[
log
20
)
(
2
2
D
T
Q
P
L
(4.85)
( )
( )
( )
(
)
.
arctg
Q
P
arctg
90
o
(4.86)
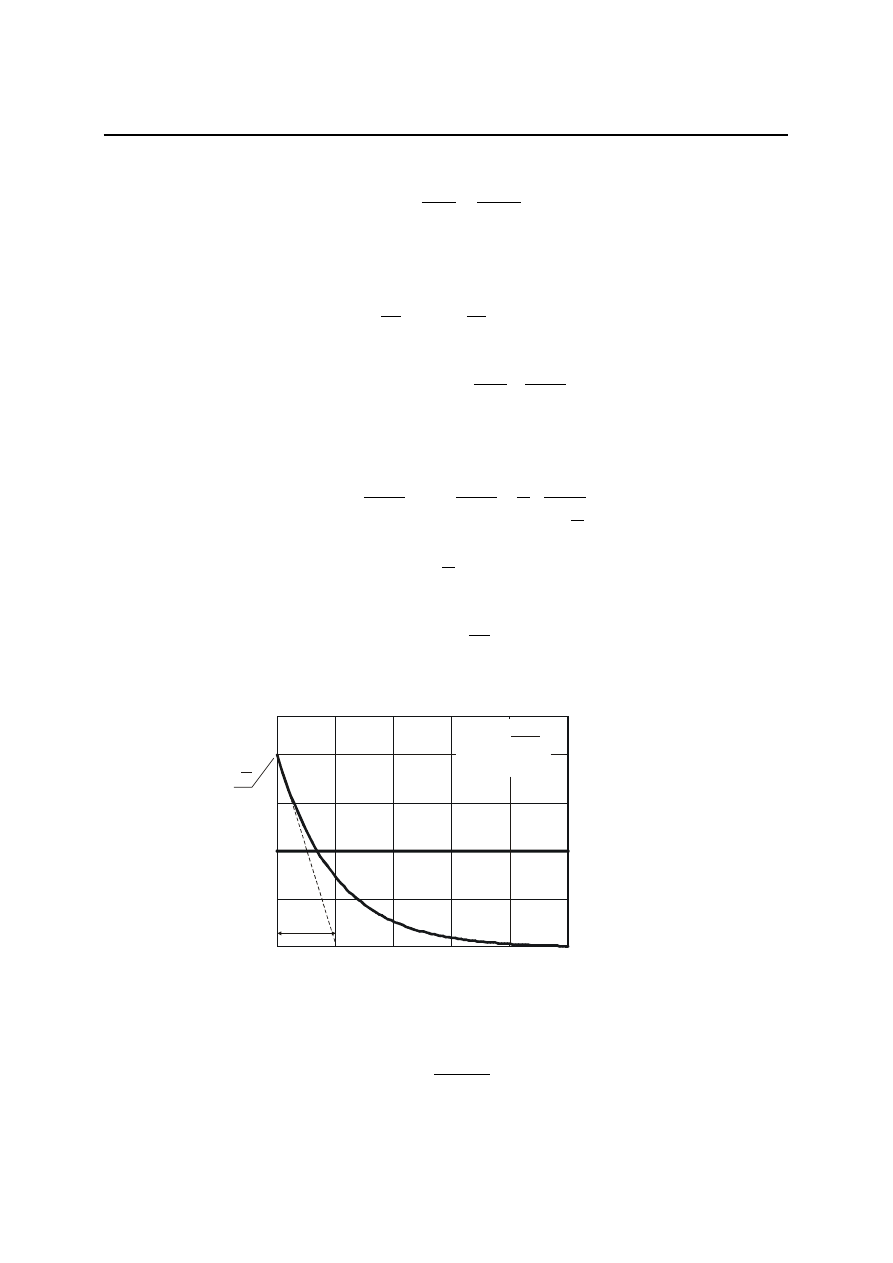
Wykresy
)
(
)
(
),
(
i
L
j
G
podano na rys. 4.29.
Rys. 4.29. Charakterystyki częstotliwościowe idealnego członu różniczkującego:
a) charakterystyka a-f, b) logarytmiczne charakterystyki amplitudowa i fazowa
Idealnego elementu różniczkującego nie można zrealizować praktycznie, ale poznanie
jego własności jest celowe z tego względu, że często w elementach złożonych wyodrębnia się
jako jeden ze składników idealne działanie różniczkujące. Ponadto, idealny element
różniczkujący traktuje się niekiedy jako pierwsze przybliżenie rzeczywistego elementu
różniczkującego.
Rzeczywisty człon różniczkujący
Ogólna postać równania rzeczywistego elementu różniczkującego jest następująca:
T
dy
dt
y k
dx
dt
,
(4.87)
a)
b)
jQ( )
P( )
G(j
)
h
20
-20
+20dB/dek
s
s
s
s
0,1
10
L( )
dB
=
1
T
90
o
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
98
skąd wynika jego transmitancja
G s
y s
x s
ks
Ts
( )
( )
( )
,
1
(4.88)
gdzie k jest współczynnikiem proporcjonalności, a T stałą czasową członu.
Jeżeli wejście i wyjście są sygnałami jednoimiennymi, równanie różniczkowe zapisuje się
w postaci
,
dt
dx
T
y
dt
dy
T
D
(4.89)
której odpowiada transmitancja
.
1
)
(
)
(
)
(
Ts
s
T
s
x
s
y
s
G
D
(4.90)
Charakterystyka statyczna będzie oczywiście identyczna z podaną na rys. 4.28 , natomiast
odpowiedź na wymuszenie skokowe wyznaczamy z transmitancji (4.88) na podstawie tablicy
przekształceń Laplace’a :
.
)]
(
[
)
(
,
1
1
1
)
(
1
)
(
/
1
T
t
e
a
T
k
s
y
L
t
y
T
s
a
T
k
Ts
ka
s
x
Ts
ks
s
y
(4.91)
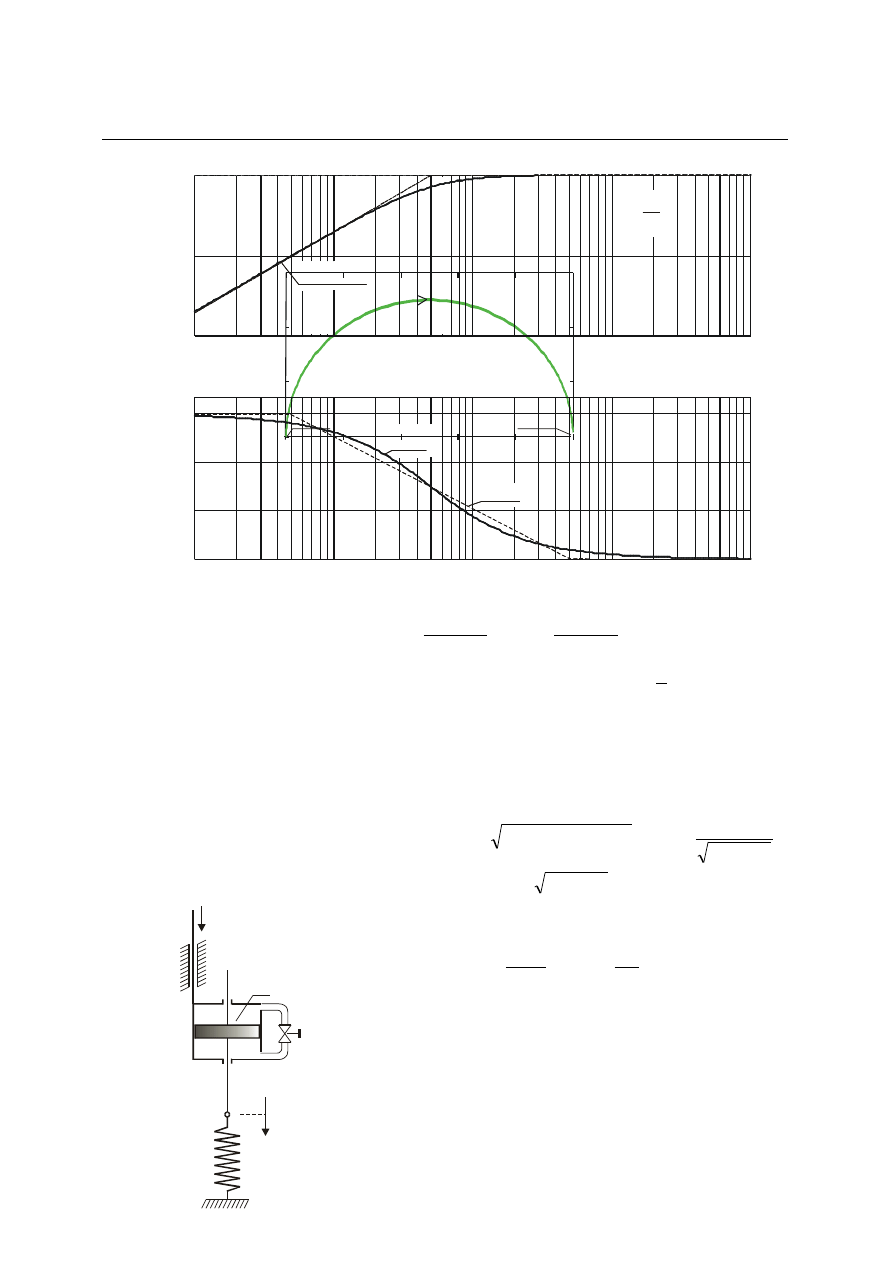
Wyznaczając tę odpowiedź z transmitancji ( 4.90) otrzymamy:
.
)
(
/ T
t
D
e
a
T
T
t
y
(4.92)
Wykres y(t) przedstawiono na rys. 4.30.
Rys. 4.30. Odpowiedź rzeczywistego członu różniczkującego na wymuszenie skokowe
Transmitancja widmowa rzeczywistego elementu różniczkującego, wyznaczona na
podstawie transmitancji operatorowej (4.90) ma postać
.
1
)
(
jT
jT
j
G
D
(4.93)
Części rzeczywista i urojona
G j
(
)
:
0
2
4
6
8
10
0.5
1
1.5
2
G(s)=
ks
Ts+1
T=2, k=4
h(t)
1(t)
t
T
k
T
99
4. Podstawowe człony automatyki
.
1
)
(
,
1
)
(
2
2
2
2
2
T
T
Q
T
TT
P
D
D
(4.94)
Wykres
G j
(
)
ma postać półokręgu o średnicy 1, ze środkiem w punkcie
0
,
2
1
j
(rys. 4.31).
Rys. 4.31. Charakterystyka amplitudowo-fazowa członu różniczkującego rzeczywistego
Logarytmiczne charakterystyki amplitudowa i fazowa:
Rys. 4.32. Charakterystyki logarytmiczne: amplitudowa i fazowa członu różniczkującego
rzeczywistego
,
1
log
20
log
20
1
log
20
)]
(
[
)]
(
[
log
20
)
(
2
2
2
2
2
2
T
T
T
T
Q
P
L
(4.95)
.
)
tg(
90
1
tg
)
(
)
(
tg
)
(
T
arc
T
arc
P
Q
arc
(4.96)
Wykresy
L( )
i
( )
przedstawiono na rys. 4.32. Liniami
ciągłymi zaznaczono charakterystyki rzeczywiste, a liniami
kreskowanymi charakterystyki asymptotyczne, przy czym
asymptotyczną charakterystykę fazową narysowano zgodnie
z aproksymacją
b
( )
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
Real Axis
Im
a
g
A
x
is
G(j )
= 0
= h
10
10
-2
-2
10
10
-1
-1
10
10
0
0
10
10
1
1
10
10
2
2
-40
-20
0
Frequency (rad/sec)
Frequency (rad/sec)
G
a
in
d
B
30
0
60
90
P
h
a
s
e
d
e
g
+20dB/dek
s
s
s
=
b
1
T
T=2
c
t
c
s
y
x
f
A
Rys. 4. 33. Tłumik hydrauli-
czny ze sprężyną
10
10
-2
-2
10
10
-1
-1
10
10
0
0
10
10
1
1
10
10
2
2
-40
-20
0
Frequency (rad/sec)
Frequency (rad/sec)
G
a
in
d
B
30
0
60
90
P
h
a
s
e
d
e
g
+20dB/dek
s
s
s
=
b
1
T
T=2

Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
100
Przykład. Tłumik hydrauliczny ze sprężyną
Schemat elementu podano na rys. 4.33. Wielkością wejściową jest przesunięcie x cylindra
tłumika, wielkością wyjściową jest przesunięcie y tłoczka tego tłumika.
Stan ustalony zachodzi wówczas, kiedy sprężyna nie jest napięta, tzn. kiedy nie wywiera
żadnej siły na tłoczek i nie powoduje przesuwania się tłoczka względem cylindra. równanie
charakterystyki statycznej jest więc
y
0
dla wszystkich x (ściśle: dla wszystkich x nie powodujących oparcia się tłoczka o dno cylindra).
Wykres tej charakterystyki pokazano na rys. 4.28.
W stanach nieustalonych siła wywierana przez ugięta sprężynę równoważona jest siłą
oporu hydraulicznego tłumika, proporcjonalną do prędkości v
w
względem cylindra
,
dt
dy
dt
dx
c
v
c
y
c
t
w
t
s
gdzie c
s
- sztywność sprężyny, c
t
- stała tłumika, proporcjonalna do powierzchni A tłoczka,
odwrotnie proporcjonalna do przekroju f szczeliny przepływowej oraz zależna od lepkości cieczy
i kształtu szczeliny przepływowej.
Oznaczając stałą czasową elementu
T
c
c
t
s
otrzymamy równanie odpowiadające postaci ogólnej (4.89)
T
dy
dt
y T
dx
dt
oraz transmitancję
G s
y s
x s
Ts
Ts
( )
( )
( )
.
1
4.5. Człony opóźniające
Równanie członu opóźniającego ma postać
,
)
(
)
(
t
x
t
y
(4.97)
skąd, na podstawie twierdzenia o przesunięciu rzeczywistym, wynika jego transmitancja
.
)
(
)
(
)
(
s
e
s
x
s
y
s
G
(4.98)
Z podanych równań wynika, że element opóźniający nie zniekształca sygnału wejściowego, lecz
jedynie przesuwa go w czasie.
Transmitancja widmowa członu opóźniającego z definicji ma postać:
,
)
(
j
e
j
G
(4.99)
a część rzeczywista i urojona
101
4. Podstawowe człony automatyki
.
sin
)
(
,
cos
)
(
Q
P
(4.100)
Logarytmiczne charakterystyki amplitudowa i fazowa dane są zależnościami:
,
0
1
log
20
)
(
)
(
log
20
)
(
2
2
Q
P
L
(4.101)
.
)
tg
tg(
)
(
)
(
tg
)
(
arc
P
Q
arc
(4.102)
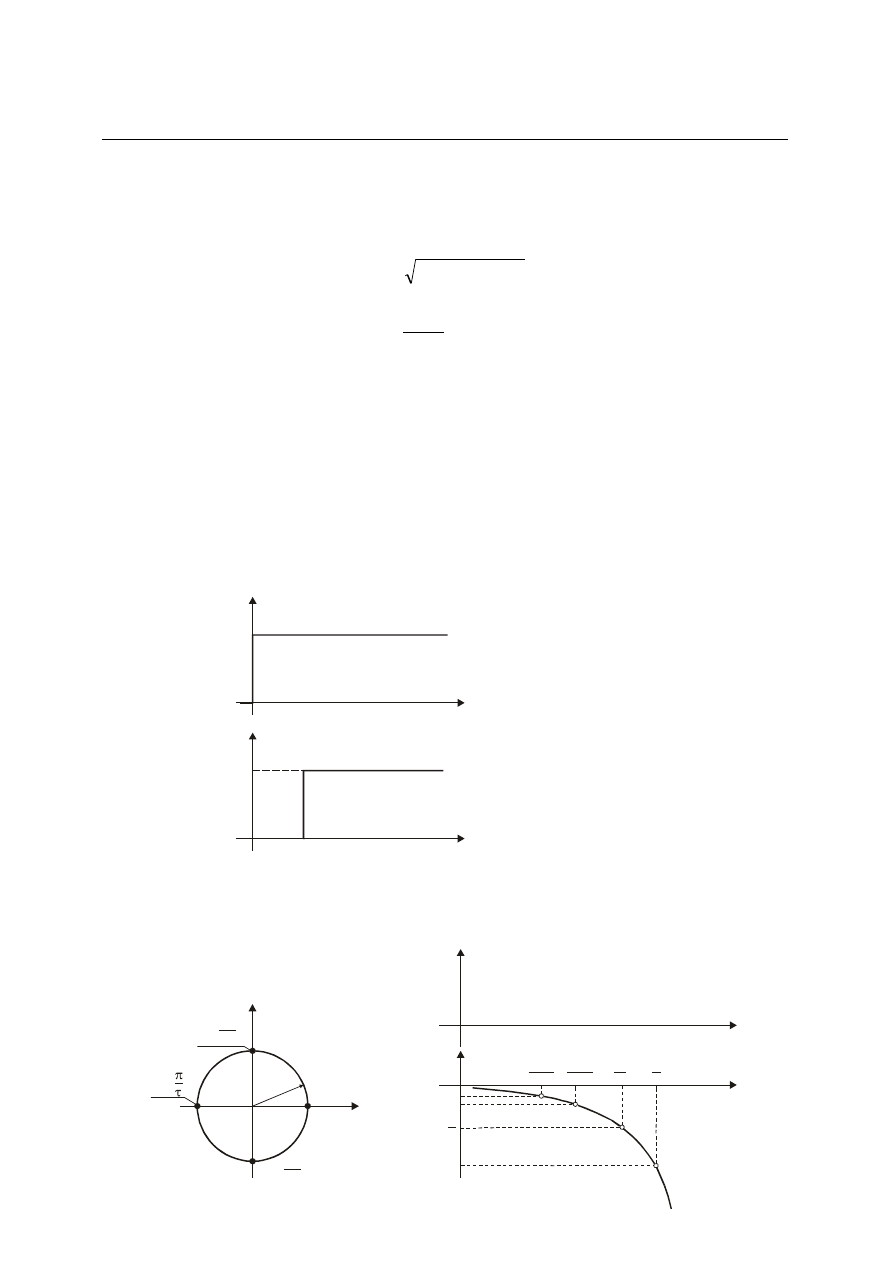
Wykresy omawianych charakterystyk członu opóźniającego przedstawione są na rys. 4.34
i 4.35. Charakterystyka amplitudowo-fazowa G(j
) ma postać okręgu o promieniu równym
jedności. Ze wzrostem pulsacji
przesunięcie fazowe
(
) osiąga coraz większe wartości
ujemne, dążąc do -
przy
dążącym do +
.
Członami opóźniającymi są w szczególności urządzenia służące do przemieszczania
(transportu) substancji, jeżeli miejsce wprowadzenia sygnału wejściowego x i miejsce odbioru
sygnału wyjściowego y znajdują się w pewnej odległości od siebie.
Rys. 4.34. Charakterystyka skokowa członu opóźniającego
Rys. 4.35. Charakterystyki członu opóźniającego: a) amplitudowo-fazowa, b)
logarytmiczne charakterystyki amplitudowa i fazowa
t
t
x(t)
x(t)
a (t)
1
a (t)
1
a
a
0
0
1
jQ( )
P( )
a)
L( )
dB
0.1
0.2
-0.1
-0.2
- 2
-
0
b)
Michał Chłędowski
WYKŁADY Z AUTOMATYKI dla mechaników
102
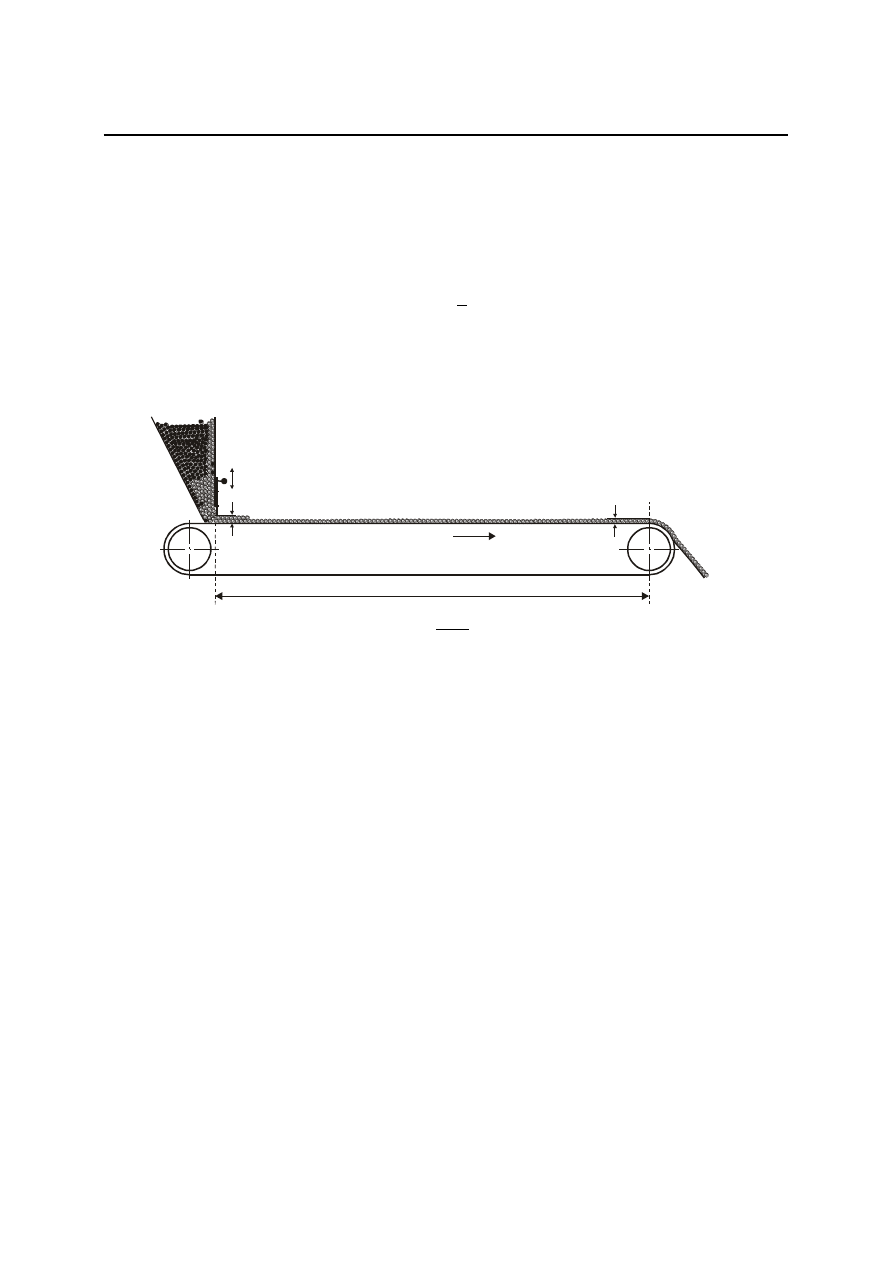
Przykład. Podajnik taśmowy
Schemat układu przedstawiony jest na rys. 4.36. Sygnałem wejściowym jest grubość x
warstwy przesyłanego materiału na początku podajnika, zaś sygnałem wyjściowym grubość y
tejże warstwy, ale na końcu podajnika.
Opóźnienie transportowe
będzie wynosić
v
l
,
gdzie: l – odległość [m], v – prędkość posuwu taśmy [m/s].
Transmitancja podajnika
.
)
(
)
(
)
(
s
e
s
x
s
y
s
G
Rys. 4.36. Schemat podajnika taśmowego
x
l
v
y
Wyszukiwarka
Podobne podstrony:
Podstawowe człony automatyki sprawozdanie
Podstawowe człony automatyki sprawozdanie1
Podstawowe człony automatyki sprawozdanie
Podstawowe czlony automatyki sp Nieznany
Podstawowe człony układu automatyki
syposz,podstawy automatyki, PODSTAWOWE CZŁONY DYNAMICZNE
Podstawowe człony regulacji
Projekt podstawowe człony dynamiczne
wstęp i podstawowe informacje, Automatyka i Robotyka, Semestr II, Ekologia i zarządzanie środowiskie
Zadania Podstawowe Elementy Automatyki
cw7 podstawowe człony dynamiczne
Podstawowe czlony1
Podstawowe czlony dynamiczne id Nieznany
podst czlony automatyki rob id Nieznany
Podstawowe czlony2
więcej podobnych podstron