Geodezja Wyższa i
Astronomia
Geodezyjna
Mgr inż. Marta
Krywanis
Geodezja Wyższa i
Astronomia
Geodezyjna
Mgr inż. Marta
Krywanis
Metodę tą stosuje się do trójkątów o
małych bokach w stosunku do
promienia kuli, przy czym wyrazy
małe wyższych rzędów zostają
opuszczone. Myślą przewodnią tej
metody jest rozwiązanie trójkątów
sferycznych, przy zastosowaniu
wzoru sinusów trygonometrii płaskiej,
po uprzedniej zmianie boków (a nie
kątów jak w metodzie Legendre’a)
Metoda Additamentów
c’ = c – (c/6R2)
c = c’+c / 6R2c’
= 22,858 858km
= 22,858 907km
a) zmniejszenie boku a:
b) obliczenie pozostałych zmniejszonych boków:
a’ = c’ (sin Awyr/ sin Cwyr )
a’ = 22,858 858km *(sin 36° 12’ 43,4205” / sin 53° 52’ 26,3805” )
a’ = 16,719 178km
a = a’+a’3 / 6R2
a = 16,719 178+0,000 019 = 16,719 197km
b’ = c’ (sin Bwyr/ sin Cwyr )
b’ = 22,858 858km*(sin 89° 54’
51,1705”/ sin 53° 52’ 26,3805” )
b’ = 28,300 358km
b = b’+b’3 / 6R2
b = 28,300 358km +0,000 093 =
28,300451km
W domu
ROZWIĄZYWANIE TRÓJKĄTÓW SFERYCZNYCH
Wzory trygonometrii sferycznej
Metoda Legendre’a
Metoda additamentów (Soldnera)
Dane:
B1 = 53° 33’ 01,7573” + n*0,0001” = 53° 33’ 01,7594”
L1 = 20° 33’ 52,3634” - n*0,0001” = 20° 33’ 52,3613”
h1 = 145,243m
A12 = 8° 07’ 35,01” + n*0,10” = 8° 07’ 37,11”
s12 = c= 22 856,807m +n*0,10m = 22 858,907m =22,858
907km
kąt 1 = A = 36° 12’ 41,32” + n*0,10” = 36° 12’ 43,42” =
0,632019695 rad
kąt 2 = B = 89° 54’ 51,17” = 1,569299077 rad
Ćwiczenie 3
Przenoszenie współrzędnych na
elipsoidzie
(Metoda średniej szerokości Gaussa)
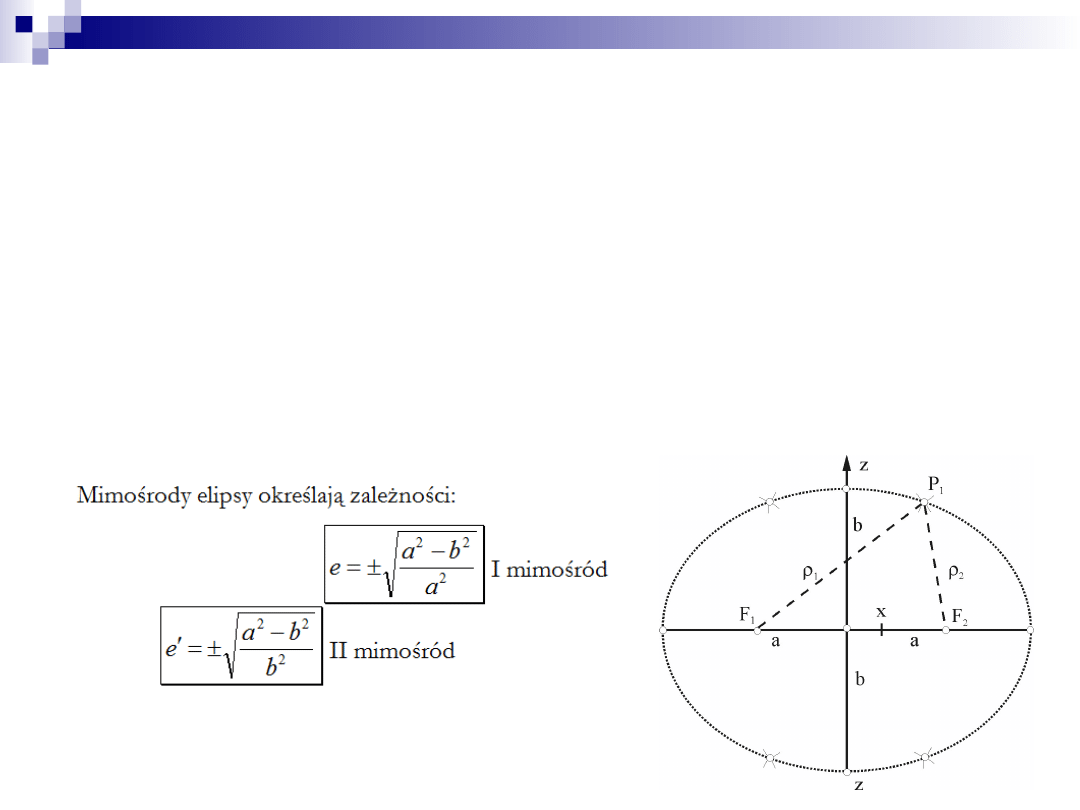
Elipsoida obrotowa – powierzchnia, którą w przeciwieństwie do geoidy
można opisać matematycznie, powstaje przez obrót elipsy wokół małej
osi.
Na osi wielkiej, po obu stronach środka, znajdują się dwa wyróżnione
punkty, F1 oraz F2 nazywane
elipsy. Ekscentryczność elipsy,
oznaczany zwykle symbolem e, to stosunek odległości między ogniskami
i długości osi wielkiej. Mimośród zawiera się w przedziale od 0 do 1, przy
czym jest on równy zeru wtedy i tylko wtedy, gdy a = b, kiedy to elipsa
jest okręgiem. Gdy mimośród
do 1, elipsa wydłuża się, a
współczynnik
dąży do nieskończoności.
Linia geodezyjna
Weźmy pod uwagę krzywą L1 położoną na danej powierzchni. Obierzmy
na tej krzywej punkt P1 i bliski punkt P2. Graniczne położenie siecznej,
gdy P2 dąży do P1 nazywamy styczną do krzywej w punkcie P1.
W punkcie P1 możemy poprowadzić nieskończenie wiele prostych
prostopadłych do stycznej. Proste te nazywamy normalnymi do krzywej
L1. Normalne tworzą płaszczyznę normalną do krzywej w punkcie P1.
Poprowadźmy przez te punkty płaszczyznę. Zmiana położenia punktów
powodować będzie zmianę położenia płaszczyzny w przestrzeni.
Graniczne położenie tej płaszczyzny, gdy punkt P2 dąży do P1 nazywamy
płaszczyzną ściśle styczną do krzywej w punkcie P1.
Wśród nieskończenie wielu normalnych do krzywej, normalna leżąca w
płaszczyźnie ściśle stycznej nazywa się normalną główną – linia
przecięcia się płaszczyzny ściśle stycznej z płaszczyzną normalną.
Linia geodezyjna
Linia geodezyjna to taka linia której
normalna główna w każdym punkcie ma
kierunek normalnej do powierzchni.
P1P2 to nieskończenie mały element linii
geodezyjnej.
Równanie przebiegu linii geodezyjnej
(ortodromy) na elipsoidzie, ma postać:
Jest to równanie Clairauta. Iloczyn promienia
równoleżnika (p=N*cosB) i linii geodezyjnej
jest wielkością stałą dla całej linii.
Klasyczny problem obliczania współrzędnych
geodezyjnych na powierzchni elipsoidy obrotowej,
azymutów i długości to przenoszenie
współrzędnych lub podstawowe zadanie geodezji
wyższej. Napotykamy dwa rodzaje problemu:
- zadanie wprost – dotyczy obliczenia
współrzędnych B2,L2 i azymutu odwrotnego A21,
linii geodezyjnej gdy znane są współrzędne B1 i L1
punktu P1, długość linii geodezyjnej s12 oraz
azymut A12 pod jakim linia geodezyjna wychodzi z
punktu P1
- zadanie odwrotne – dotyczy obliczenia długości
linii geodezyjnej s12 łączącej na powierzchni
elipsoidy dwa punkty o znanych współrzędnych
P1(B1, L1) i P2(B2, L2) oraz obliczenia azymutów
linii geodezyjnej (wprost i odwrotnego) A12 , A21.
Zadanie
Wyznaczyć współrzędne drugiego końca linii geodezyjnej
oraz azymut odwrotny (zadanie wprost). Rozwiązując
zadanie wykorzystać metodę średniej szerokości Gaussa.
Dane:
B1=[50+M]36’39,515”
L1=[18+M]25’25,633”
A1=[20+M]52’6,9196”
S=24092,926+N1000 m
a=6378137 m
e^2=0,0066943800229
e’^2=0,00673949677548
M=
N=
( w rad, 9 miejsc po przecinku, a
ostatecznie w stopniach)
B
2
przybl
=
ΔL
przybl.
=
L
2
przybl
=
A
2
przybl
=
B=
l=
b=
t=
2
=
v=
Δ=
B
2
-B
1
=
Δ=
L
2
-L
1
=
=
A
2
-A
1
=
B2=
L2=
A2=
4. Kolejna iteracja z wykorzystaniem
obliczonego B.
B=