PRELIMINARIES AND PROPERTIES OF NUMBER SETS

Lecture 1

I hear and I forget.

I see and I remember.

I do and I understand.

---Chinese Proverb

ASSESSMENT of ALGEBRA COURSE

The unit consists of two components:

the lecture

the classroom tutorials.

In order to pass the unit first you must pass the tutorial
component and then pass the final exam at the end of the
semester.
During this semester you will take two tests. The dates of
the tests will be announced at least one week before the
tests take place.
You can obtain from each test at most 50 points.

To pass the tutorials you have to pass each test,
obtain 25 or more points from each test

.

If you obtain a sum of more than 80 points (grades
4+ or 5) from both of the tests you are exempt
from the examination (you don't have to take the
exam)

Points

Grad

e

Remark

[100,

90]

5

Excellent

(90,

80]

4+

Very Good

(80,

70]

4

Good

(70,

60]

3+

Fair

(60,

50]

3

Satisfactory

(50, 0]

2

Fail

Tutorial Classification:

If you don’t pass one or both of the tests you can

retake

the test/tests

at the end of the semester. In this case you obtain

at most grade at

level 4

(meaning that you can not be exempt from the examination).

To pass the exam you have to obtain 50% of the maximum score.

Text-books:

1,

“Algebra Liniowa 1,2”,

T. Jurlewicz, Z.Skoczylas, GiS

Wroclaw (you can buy it in the “basement” book store or
from senior students),

2.

“Theory and problems of matrices”,

F. Ayres Jr,

3.

"Matrix Analysis and Applied Linear Algebra

", C. D.

Meyer,

4. “Linear Algebra with Applications”,

G. Williams

5. “Linear Algebra with Applications”,

O.Bretscher

6. “Linear Algebra with Applications”,

S.J.Leon

or any other text-book, at university level, on Algebra.

Useful links:

http://mathforum.org/library/drmath/drmath.college.html

http://www.clarku.edu/~djoyce/complex/
http://www.math.odu.edu/~bogacki/lat/
http://www.ping.be/~ping1339/lintf.htm
etc.

library

ALGEBRA,
the word was derived from the title of a book written
in the yearly 800s, by

Mohammed Ibn Musa Al-Khowarizimi

Al Jabr Wa'l Muqabalah

It is concerned with straightforward solutions of equations
of first and second degree.

The title of the book means
"restoration by transposing terms from one side of an equation
to the other".

C: 1+ i, 2 +
3i,...

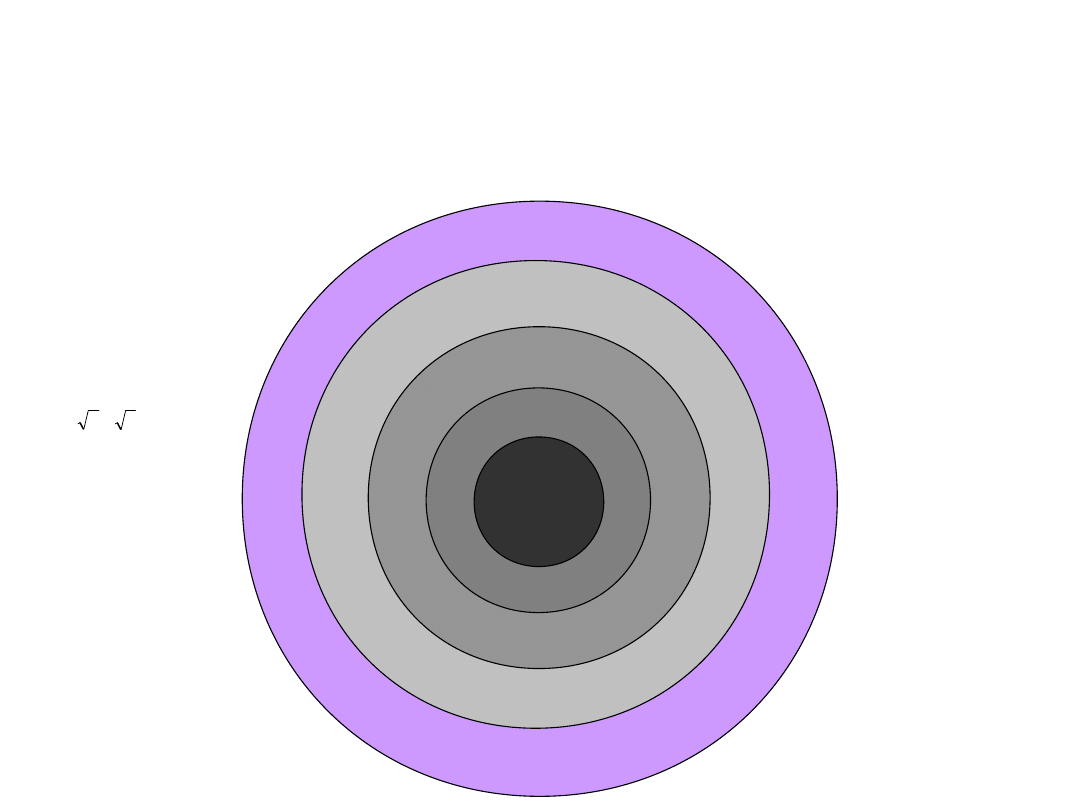
NATURAL

‘N’

INTEGERS ‘Z’

RATIONAL ‘Q’

REAL ‘R’

Leopold Kronecker:
„God Himself made the natural numbers; all else is the work of man”



,

,

,

e

5

2

7

COMPLEX ‘C’

Z: -1, -2, -3 ...

Q: 1/2, -1/2, 5/7...

R: ,

-
0.875

0

1

2

1

2

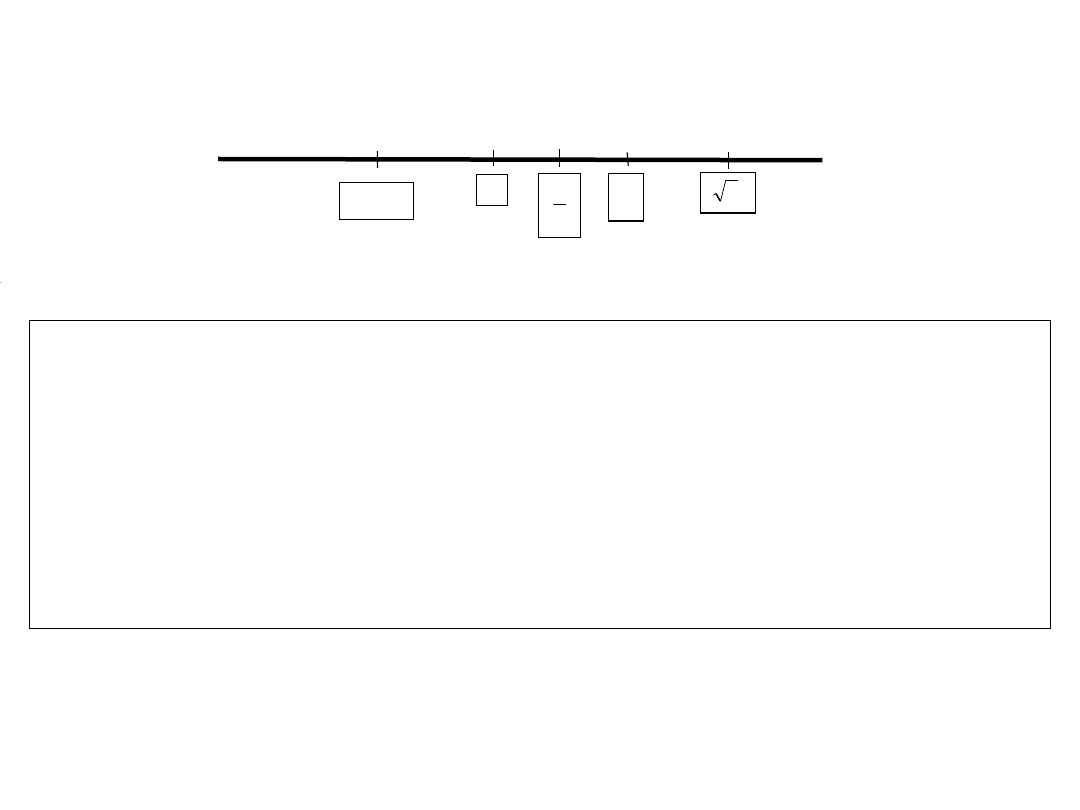
Numbers as points on a line

1.

Natural numbers

: 0, 1, 2, 3, 4, 5, .....

2.

Integers

(to subtract)

-4, 4,-9,...

3.

Rationals (to divide)

1/2, -4/6, 5/567,...

The rationals do not fill the whole line. To supplement them we
introduce
4.

Real numbers

(to fill up the whole line, divide area)

: 1, 0.2,

-0.5, , , ...

(are defined by limits of rational sequences or pairs of intervals)

Complex numbers

(to solve x

2

= -1)

are pairs of real numbers:

(3, 0) = 3 + i , (1,1) = 1+i , (0,1) = i

Other examples of 'number' sets and operations on them.

INTEGERS: ... , -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...

Lets choose every third number,

... ,

-9

, -8, -7,

-6

, -5, -4,

-3

, -2, -1,

0

, 1, 2,

3

, 4, 5,

6

, 7, 8,

9

, ...

... ,-9,

-8

, -7, -6,

-5

, -4, -3,

-2

, -1, 0,

1

, 2, 3,

4

, 5, 6,

7

, 8, 9, ...

... , -9, -8,

-7

, -6, -5,

-4

, -3, -2,

-1

, 0, 1,

2

, 3, 4,

5

, 6, 7,

8

, 9, ...

glue them together

... ,

-9

, -8, -7,

-6

, -5, -4,

-3

, -2, -1,

0

, 1, 2,

3

, 4, 5,

6

, 7, 8,

9

, ...

... ,-9,

-8

, -7, -6,

-5

, -4, -3,

-2

, -1, 0,

1

, 2, 3,

4

, 5, 6,

7

, 8, 9, ...

... , -9, -8,

-7

, -6, -5,

-4

, -3, -2,

-1

, 0, 1,

2

, 3, 4,

5

, 6, 7,

8

, 9, ...

and call them ‘supernumbers’

0

1

2







How do we add and multiply
‘superumbers”?

Definition
For ‘supernumbers’ 0,1,2 let us define:

SuperAddition:

(p + q)

SUPER

= remainder after dividing p + q

by 3,

SuperMultiplication:

(p

 q)

SUPER

= remainder after dividing p



q by 3.

+

0

1

2

0

0

1

2

1

1

2

0

2

2

0

1

0

1

2

0

0

0

0

1

0

1

2

2

0

2

1



OR a  b (mod m) iff

the numbers a and b have the same remainder when divided by m.

Example
1. for all

a  b (mod 1).

(The remainder is zero)

2.

8  13 (mod 5)

because

(13 - 8) = 1· 5
or 8=1·5 + 3 and 13=2·5 + 3

3.

-17  1 (mod 6)

because

(1+17) = 3· 6
or -17= -3·6 + 1 and 1=0·6 + 1

Can we generalise the above ‘supernumbers’?

Yes,

and we obtain the congruence ‘modulo m’.

*

iff = ‘if and only if’

Definition
Numbers are congruent modulo m,
a  b (mod m) iff

*

m |( b – a ).

Read:

a is congruent to b modulo

m.

gluing

PROPERTIES

(reflexiv)

a  a (mod m);

(symmetric) a  b (mod m) then b  a (mod

m);

(transitive) a  b  c (mod m) then a  c (mod

m).

The congruence class (equivalence class) of the integer a is
denoted by
[a]

n

= { ..., a − 2n, a − n, a, a + n, a + 2n, a + 3n, ...}.

PROPERTIES

If a  b (mod m) and c  d (mod m),

then:

1. a + c  (b + d) (mod m)

2. a



c  (b  d) (mod m)

3. a

N

 b

N

(mod m).

Definition (modulo operations)

p, q are integers

(p + q) (mod m) = remainder after dividing p + q by m,
(p



q) (mod m) = remainder after dividing p



q by m.

The sum and product of 'glued' numbers

NOTE !!!!!

There is another

similar notation

in Computer Sciences: the modulo operation.

It is the remainder in division sometimes written as "

mod

",

so we write "

14 mod 12 = 2

".

This meaning of "mod" is different from the congruence "mod"

it is true to say "

38 ≡ 14 (mod 12)

" ,

but it is

not true to say "38 = 14 mod 12"

— 38 is congruent to 14

modulo 12,
but the remainder of 14 divided by 12 is 2, not 38.

To avoid this confusion,
the congruence relation is sometimes expressed by using modulo
instead of mod
like "38 ≡ 14 (modulo 12)" in computer science.

In

CRYPTOGRAPHY

, modular arithmetic is used in public key systems

such as RSA and Diffie-Hellman, and is used in and a variety of
symmetric key algorithms including AES, IDEA, and RC4.

In

COMPUTER SCIENCE

, modular arithmetic is often applied in

bitwise operations and other operations involving fixed-width,
cyclic data structures.

In the

VISUAL ARTS

, modular arithmetic can be used to create

artistic patterns based on the multiplication and addition tables modulo n.

In

MUSIC,

modular arithmetic is used, where octave and enharmonic

equivalency occurs.

APPLICATIONS

POSITIONAL NUMBER SYSTEMS

The previously proven facts give the possibilities to express the
notation of
a number in another positional system other than the popular
decimal one.

Let us fix a natural number m > 0, which shall be treated as
the base of the positional system.

Theorem
Every natural number can be uniquely represented as:
n = a

k

m

k

+ a

k-1

m

k-1

+ ..... + a

1

m + a

0

, where 0

 a

0

< m.

The number

m is called the base

of the system.

The number n, with fixed m, is represented by a system of coefficients
a

k

a

k-1

... a

1

a

0

which is the representation of n in a system of

base m;

a

k

, a

k-1

, ... ,a

0

are the digits

in this representation.

One can convert a number from base n to
base m.

2 binary

3 ternary
4 quaternary
5 quinary
6 senary
7 septimal

8 octal

9 monary

10 decimal

12 duodecimal

16
hexadecimal

Every real number can be represented by a "nonterminating
decimal"

POSITIONAL NUMBER SYSTEMS OF BASE N

Sometimes three or four of the digits are grouped together,
this means that the new base is 2

3

(octal)

or 2

4

(hexadecimal).

A

bit

refers to a digit in the binary numeral system

(base 2).
(

b

inary

dig

it

)

For example, the number 1001011 is 7 bits long.

A

bit

of storage is like a light switch; it can be either on (

1

) or off (

0

).

A single bit is a one or a zero, a true or a false, a "flag" which is "on" or "off",

Binary digits

are almost always used as the basic unit of

information storage and communication in digital computing.

DEFINITION

The

prime numbers

are those natural numbers p, excluding p =

0, p = 1 which are only divisible by 1 and itself,

i.e. for every natural n: if n |p then n = p or n = 1.

The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19,...

Fundamental Theorem of Arithmetic

Any integer N can be represented as a product of primes.
Such a representation is unique up to the order of prime factors

6 = 2·3, 15 = 3 ·5, 36 = 2 ·2 ·3 ·3

DEFINITION

For non-negative integers m

1

, m

2

, ..., m

k

,

their

Greatest Common Divisor

is defined as

 GCD(m

1

, m

2

, ..., m

k

) = max{s: s|m

i

, for i = 1, ..., k},

where, as always, "s|m" means that s divides m exactly.

The Greatest Common Divisor

- the largest number which divides all m

1

, m

2

, ..., m

k

The algorithm is based on the following two observations

:

1. If b|a then GCD(a, b) = b.
This is indeed so because no number (b, in particular) may have
a divisor greater than the number itself (I am talking here of non-negative

integers.)

2. If a = bt + r, for integers t and r, then GCD(a, b) = GCD(b, r).

Indeed, every common divisor of a and b also divides r.
(a)Thus, GCD(a, b) divides r.
(b) And of course, GCD(a, b) divides b.
Therefore, GCD(a, b) is a common divisor of b and r and hence GCD(a, b) ≤

GCD(b, r).

The reverse GCD(b, r) ≤ GCD(a, b)

is also true because

every divisor of b and r also divides a.

EUCLID'S
ALGORITHM

Given two numbers a,b not prime to one another, find their
greatest common divisor.
GCD(a,b)=?

!

Corollary
For every pair of whole numbers a and b there exist
two integers

s

and

t

such that a

s

+ b

t

= GCD(a, b).

Example
2322×20 + 654×(-71) = 6.

Example 1
Use the Euclidean Algorithm to find the GCD(13013, 390).
a=

13013

, b =

390

.

a = b · t + r

13013

=

390

 33 + 143,

390

= 143 2 + 104

143 =104  1 + 39

104 = 39  2 + 26

39 = 26  1 + 13

26 = 13  2 + 0

GCD(13013, 390) = 13.

First mentions:
by Brahmagupta (बबबबबबबबबबब) (589–668) an Indian
mathematician and astronomer.

The Chinese Remiander Theorem
Introduction

The original form of the theorem, was contained in a third-
century AD book by a Chinese mathematician Sun Tzu.

It is a statement about simultaneous congruences.

Counting the number of soldiers in an army.

The general has the soldiers quickly line up in groups of 3, 5, 7, 11
and counts the remaining soldiers that can't make complete groups.

After enough of these tests are made, the general can quickly calculate
how many soldiers he has exactly;

thus he has done a 3 hour ‘headcount’

in 2 minutes.

The larger the product n = p

1

...p

k

the more accurate we are.

Chinese Remainder Theorem

Suppose p

1

, p

2

, ..., p

n

are positive integers which are pair wise relatively

prime

(meaning GCD( p

i

, p

j

) = 1 whenever i  j) .

Then for any given integers q

1

, q

2

, ...,q

n

,

there exists an integer q solving the system of simultaneous

congruencies :

q  q

i

(mod p

i

) for i =1…n.

Furthermore, all solutions x to this system are

congruent modulo the product n = p

1

...p

k

i.e. can be obtained by adding a multiple of n = p

1

...p

k

to x

Example
Find a number q, which divided by 5 will give remainder 3, and which

divided by 7

will give remainder 4:
q  3(mod5) i.e. q = 5·k + 3

q  4(mod7) i.e. q = 7·m + 4

We have to find k and m such that 5 · k + 3 = 7 · m + 4
or 5 · k - 7 · m = 1
--------------------------------------------------------------------------------------------------------

----

The Euclid's Algorithm:
7 = 5·1 + 2  2 = 7 - 1·5

5 = 2·2 + 1  1 = 5 - 2·2

2 = 1·2 + 0
--------------------------------------------------------------------------------------------------------

----

So we can write
1= 5 - 2·2 = 5 - 2·(7- 1·5) = 5 - 2·7 + 2·1·5 =

| we group the terms with ‘5’

and the terms with ‘7’ |

= 3 ·5 - 2 ·7

5 · 3 - 7· 2 = 1

We see that k = 3 and m = 2, so q = 5·3 + 3 = 18.

Thus one of the possible solutions can be number q = 18 or
all solutions q = 18 + n·5·7 for any integer n.

THE CIPHER ALGORITHM:

RSA algorithm – public key cryptography (by Ronald Rivest, Adi

Shamir, Leonard Adleman)

1. We have to choose two prime numbers P and Q (large ones
more than 1024 – bit),
2. Calculate the product N = PQ,
3. Choose a special E – using PQ and (P-1)(Q-1) (on next page),
4. Compute a D using PQ and (P-1)(Q-1) (on next page),
5. Destroy P and Q.

We have

(PQ, E) - the public key

, (PQ – modulus, E - public exponent)

D - the private key

– very secret!!! (D – private exponent)

You can publish your public key freely, because there are no
known fast and easy methods of calculating D, P, or Q given
only

(PQ, E)

(your public key).

If

P

and Q are each 1024 bits long, the sun will burn out

before the most powerful computers presently in existence
can factor your modulus into P and Q.

We have two large P and Q.

We choose E such that E is greater than 1, E is less than PQ, and E
and
(P-1)(Q-1) are relatively prime. E does not have to be prime, but it
must be odd.

Compute D such that (DE - 1) is evenly divisible by (P-1)(Q-1). We
write this as DE = 1 (mod (P-1)(Q-1)).

The encryption function is

C = T

E

(mod PQ)

where C is the encripted text (a positive integer), T is the plaintext (a
positive integer). The message being encrypted, T, must be less than
the modulus, PQ.

The decryption function is

T = C

D

(mod PQ)

EXAMPLE (for primes P=5, Q=17)

PQ

=

85

= 5  17 (public),

E

=

5

(public exponent),

D

=

13

(private)
(

P

-1)(

Q

-1) = 64 GCD(

E

, 64) = 1

64|(

5

D

- 1 )

Decrypting

(with the use of the private key

D

=

13

):

79

13

(mod 85) = 24.

So we recovered the original message x.

We want to

encrypt

the letter ‘x’ = 24

(x is the 24-th letter of

the alphabet)

24

5

(mod

85

) = 79 .

The encryptyed ‘x’ is 79.

Rev. Euklid

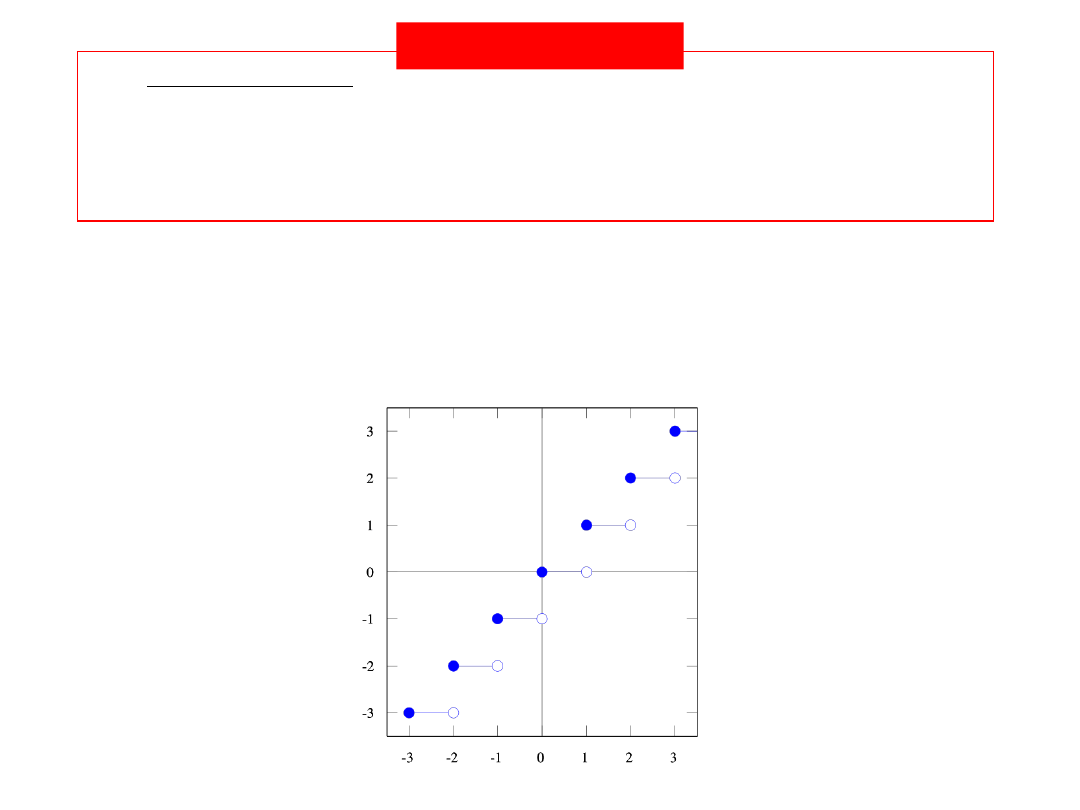
The floor function of a real number x, denoted

 

   or

floor(x),

is the largest integer less than or equal to x i.e.

 

x

 





x

n

Z

n

x







:

sup

For example: floor(2.9) = 2, floor(−2) = −2 and floor(−2.3)
= −3.

For nonnegative x, a more traditional name for floor(x)
is
the integral part or integral value of x sometimes
denoted by E(x)

The floor function

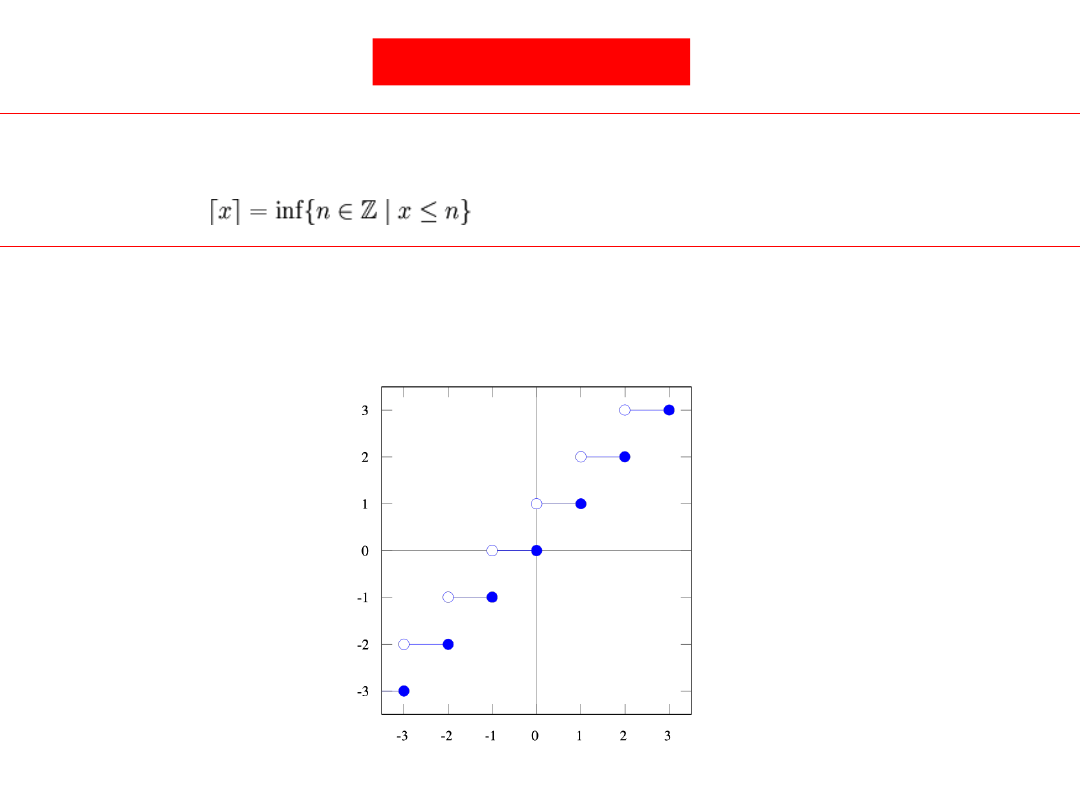
The ceiling function, given x, ceiling(x) also denoted by

 

     is the function

defined as

 

        . This is, the smallest integer not less than x.

The ceiling function

For example, ceiling(2.3) = 3, ceiling(2) = 2 and ceiling(−2.3) = −2.

 

x