ALGORYTMY

GRAFOWE

 

 

PRZESZUKIWANIE W GŁĄB

{ "Odwiedza" każdy wierzchołek grafu G ; 
    Wierzchołki “odwiedzone” mają  kolor czarny }

DFS-VISIT (u);
{"Odwiedza" wierzchołki  
składowej  spójności 
zawierającej wierzchołek u }

     begin
 1.     kolor (u) := SZARY;
 2.     for każdy  v Adj (u)  do

 3.          if kolor (v) = BIAŁY
 4.              then   DFS-VISIT 
(v);  
 5.      kolor (u) := CZARNY;

     end;       

DFS (G);

   

begin

 1.  for każdy  u  V(G)  do

 2.         kolor (u) := BIAŁY;

 3.   for każdy  u V(G)  do

 4.          if kolor (u) = BIAŁY
 5.               then  DFS-VISIT 
(u);
    end;

 

 

PRZESZUKIWANIE    WSZERZ

BFS (G,s);

{Jeśli G jest spójny, to odwiedza każdy wierzchołek grafu  G, 
 jeśli niespójny, to odwiedza każdy wierzchołek składowej 
spójności zawierającej wierzchołek s .Wierzchołki “odwiedzone” 
mają kolor czarny }

begin

1. for każdy uV(G)–{s} 

do
2.        kolor (u) := BIAŁY;
   
3. kolor (s) := SZARY;

4.  Q := {s};

while  Q <>   do

    begin
1.      u:= head (Q);
2.      for każdy  v  Adj (u)  do

3.          begin
4.             if kolor (v) = BIAŁY
5.                then  begin
6.                              kolor (v) = 
SZARY;

 

7.

                              ENQUEUE 

(Q,v);

              end;
end;

8.         DEQUEUE (Q);    
9.        kolor (u) := CZARNY;
    end    end;

          

 

 

MST-KRUSKAL (G, w);

{ 

Wyznacza zbiór ET krawędzi minimalnego drzewa spinającego 

   spójnego grafu G 

}

begin

   ET := ;

   for  każdy v  V(G) do

       MAKE – SET (v);

   posortuj krawędzie  z E(G)
   niemalejąco względem wag w ;

 for każda  krawędź  {u,v}  E(G) 

  (w kolejności  niemalejących wag)
 do
      
    if  FIND-SET (u)  <> FIND-SET (v) 
        then 
           begin
               ET := ET  {{u,v}};

               UNION (u,v)
            end ;
 
  return ET
end ;

 

 

MST – PRIM (G, w, r ); 

{ Wyznacza  zbiór krawędzi   ET = { {v, 



(v)}: v 



V(G) – {r} }

    minimalnego drzewa spinającego  spójnego grafu G }

 

begin

     Q := V(G);
     for każdy u  Q do

           key(u) := ;

     key(r) :=  0;
     (r) := NIL;

  while  Q <>  do

      begin
          u := EXTRACT-MIN (Q);
          for każdy v  Adj(u) do

                if  v  Q  and w(u,v) < key(v)

                    then  
                        begin
                            (v) := u;

               key(v) := w(u,v)

                        end
      end
end;

                           

 

 

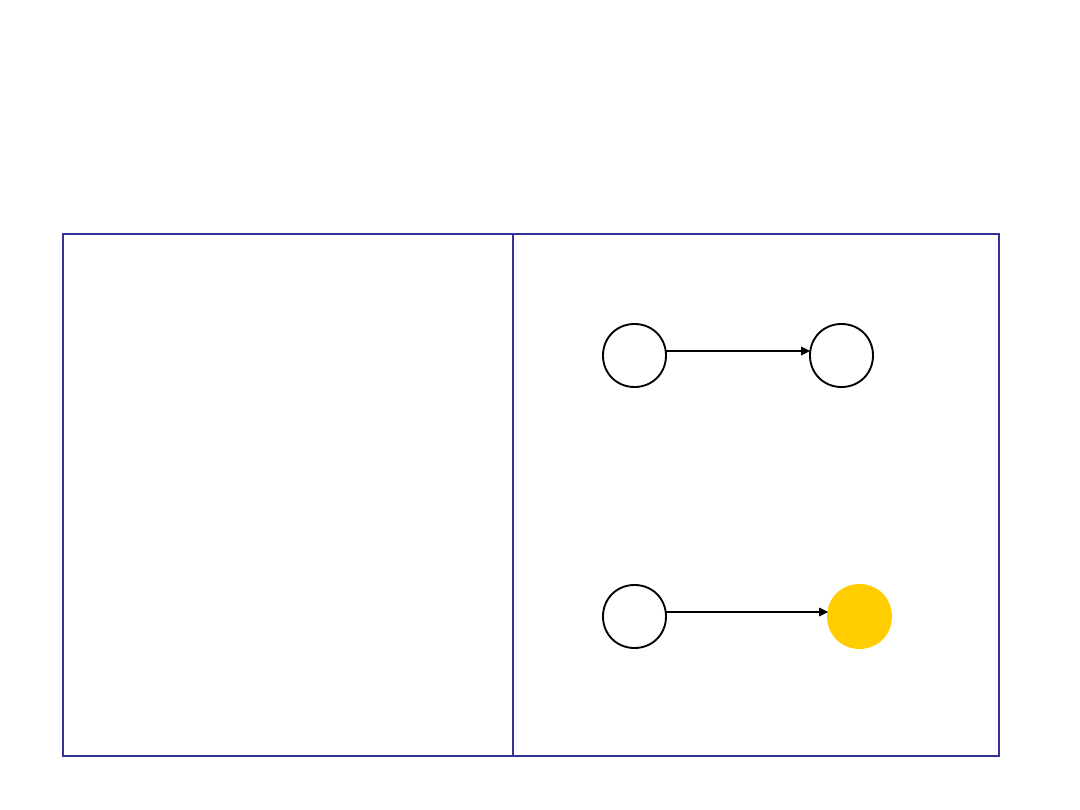
RELAX (u, v, w);

{ Może zmniejszyć wartość d(v) i zmienić  



(v) }

begin

    if  d(v) > d(u) + w(u,v)
       then 
            begin
                 d(v) := d(u) + w(u,v);
                 (v) := u

            end
 end;

4

9

7

4

3

3

u

v

u

v

 

 

DIJKSTRA  (G, w, s);

{ Wyznacza odległość każdego wierzchołka grafu G od wierzchołka s }

begin
  for każdy v  V(G) do

      begin
          d(v) := ;

          (v) := NIL;

       end;

   d(s) := 0;

S := ;

 Q := V(G);

   while  Q <>  do

       begin

           u := EXTRACT-MIN (Q);
           S  := S  {u};

           for każdy v  Adj(u) do

                RELAX (u, v, w);

        end
  end;

 

 

begin

  for każdy v  V(G) 

do
      begin
          d(v) := ;

          (v) := NIL;

       end;

   d(s) := 0;

BELLMAN – FORD (G, w, s);

{ Testuje czy graf ma cykle ujemnej długości ;
  jeśli nie ma, to znajduje odległość każdego wierzchołka grafu 
G 
  od wierzchołka s }

for i := 1 to |V(G)| - 1  do
         for każda  krawędź {u,v}  E(G) do

               RELAX (u, v, w);

   for każda  krawędź {u,v}  E(G) do

         if d(v) > d(u) + w(u,v)
              then  return  FALSE;

   return TRUE

 end;

 

 

begin
  for każda krawędź 
(u,v)E(G)

  do
    begin
          f(u,v) := 0;
          f(v,u) := 0
    end;

 while istnieje ścieżka P

st

 

    w  sieci residualnej G

f 

  do

      begin
         c

f

 (P

st

) := min { c

f

 (u,v) : (u,v)  

P

st 

};

         for każda krawędź (u,v)  P

st

  

do
             begin
                  f(u,v) := f(u,v) + c

f

 (P

st

);

                  f(v,u) :=  f(u,v);

             end
       end

end

FORD-FULKERSON (G,c,s,t) ;

{

 

Jeśli c przyjmuje wartości całkowite, to algorytm wyznacza

  maksymalny przepływ z s do t   w sieci  (G,c,s,t ) } 

 

 

begin
   for każdy wierzchołek u 
V(G)

     do
         begin
             h(u) := 0;
             e(u) := 0
         end;
   for każda krawędź (u,v)  

E(G)
      do
         begin
             f(u,v) := 0;
             f(v,u) := 0
         end;
   h(s) := V(G);

 

for każdy wierzchołek u  Adj 

(s)  do
       begin
            f(s,u) := c(s,u);
            f(u,s) :=  c(s,u);

            e(u) := c(s,u)
        end;

  while  można zastosować  
              PUSH  lub LIFT  do

      wybierz PUSH lub LIFT i 
wykonaj ;

end;

PREFLOW (G,c,s,t);

{Wyznacza maksymalny przepływ z s do t w sieci (G,c,s,t) }

 

 

PUSH (u,v) ;

{ Stosujemy gdy:
     e(u) > 0  
     i  c

f 

(u,v) > 0 

 

       

i  h(u) = h(v) + 1 }

begin
    d

f

 (u,v) := min { e(u), c

f

 

(u,v) };
    f(u,v) := f(u,v) + d

f

 (u,v);

    f(v,u) :=  f(u,v);

    e(u) := e(u) - d

f

 (u,v);

    e(v) := e(v) + d

f

 (u,v)

end;

 

LIFT (u) ;

{ Stosujemy gdy:
  e(u) >  0 
 i 



 (v



V)   jeśli (u,v)



 E(G

f

 ) , 

                     to h(u) <= 
h(v) ) }

begin
   h(u) := 1 + min { h(v) : (u,v)  

E(G

f

 ) }

end;

OPERACJE PUSH I LIFT