Chemical Engineering Science, Vol. 53, No. 18, pp. 3189—3197, 1998

( 1998 Elsevier Science Ltd. All rights reserved

Printed in Great Britain

PII: S0009–2509(98)00103–1

0009—2509/98/$—See front matter

Numerical study on

sublimation–condensation phenomena

during microwave freeze drying

Zhao Hui Wang* and Ming Heng Shi

Department of Power Engineering, Southeast University, Nanjing 210018, People’s Republic of

China

(Received 20 September 1997)

Abstract—A sublimation—condensation model is developed for freeze drying of unsaturated
porous media. The governing equations describing the drying process are solved numerically
with variable time step finite-difference method. The sublimation—condensation phenomena
during microwave freeze drying are studied numerically for different operating conditions
including electric field strength, sample thickness, and vacuum pressure. The results show that
the sublimation—condensation effects depend on different drying conditions. For larger electric
field strength, vapor transfer in sublimation—condensation region is more intensive and larger
part of the vapor is sublimated from this region, so the effect of sublimation—condensation
region on drying time is more significant. Too large electric field strength is not necessary for
microwave freeze drying. In case of larger sample thickness, the saturation change of the
sublimation—condensation region is larger, and the effect of sublimation—condensation region
on drying time is more significant. The effect of vacuum pressure on drying time is not so
significant in the observed range.

( 1998 Elsevier Science Ltd. All rights reserved.

Keywords: Drying; heat transfer; mass transfer; numerical analysis; porous media.

INTRODUCTION

In spite of the high cost, the demand for freeze-dried
products has been growing rapidly, and the freeze
dehydration has been applied as a key operation in
many new areas. In order to decrease the drying time
and increase the product quality, many ways to en-
hance the heat supply have been investigated.

The earliest work on heat and mass transfer mecha-

nism of freeze drying concentrated on the basic trans-
port phenomena. The transport properties such as
permeability, diffusivity, and thermal conductivity of
the materials dried were measured experimentally un-
der the conditions of low temperature and vacuum
pressure (Harper, 1962; Lusk et al., 1964; Massey and
Sunderland, 1967; King et al., 1968). In 1967, Sandall
et al. predicted the freeze drying rate with a pseudo-
steady model of heat and mass transfer, and Dyer and
Sunderland (1967) suggested a simple transient heat
transfer model for the freeze drying. As a significant
improvement, Fox and Thomson (1972) analyzed the
freeze drying process with an unsteady drying model
of coupled heat and mass transfer. Ma and Peltre
(1975) proposed an unsteady heat and mass transfer
model with internal heat generation for microwave

*Corresponding author. E-mail: [e-mail].

freeze drying. Numerical analysis was employed in
their research of freeze-drying process for the first
time.

After the Luikov’s theory (1975) of heat and mass

transfer in porous media was presented on the basis of
the irreversible thermodynamics, the study on heat
and mass transfer of freeze drying got to focus on the
solution to this model and the analysis of transport
mechanisms by using this model. Lin (1981, 1982)
obtained the analytical solutions in cases of constant
and variable temperature of sublimation front. Fey
and Boles (1987a, b) studied the effects of convection
heat transfer and compared the mass transfer between
the Darcy’s flow and the Fick’s diffusion with their
analytical solution.

All the models discussed above considering that

phase change of freeze drying at the sublimation inter-
face are called sublimation interface model. Fey and
Boles (1988) considered the frozen materials with
frozen water initially partially and fully filled and
proposed a model to describe the heat and mass
transfer in the unsaturated frozen region based on the
Luikov’s system. The water vapor recondensation
process in the frozen region was analyzed in this
model, but the saturation change of frozen region
caused by recondensation was not considered. The
transport coefficients in the model were also con-
sidered as constant.

3189

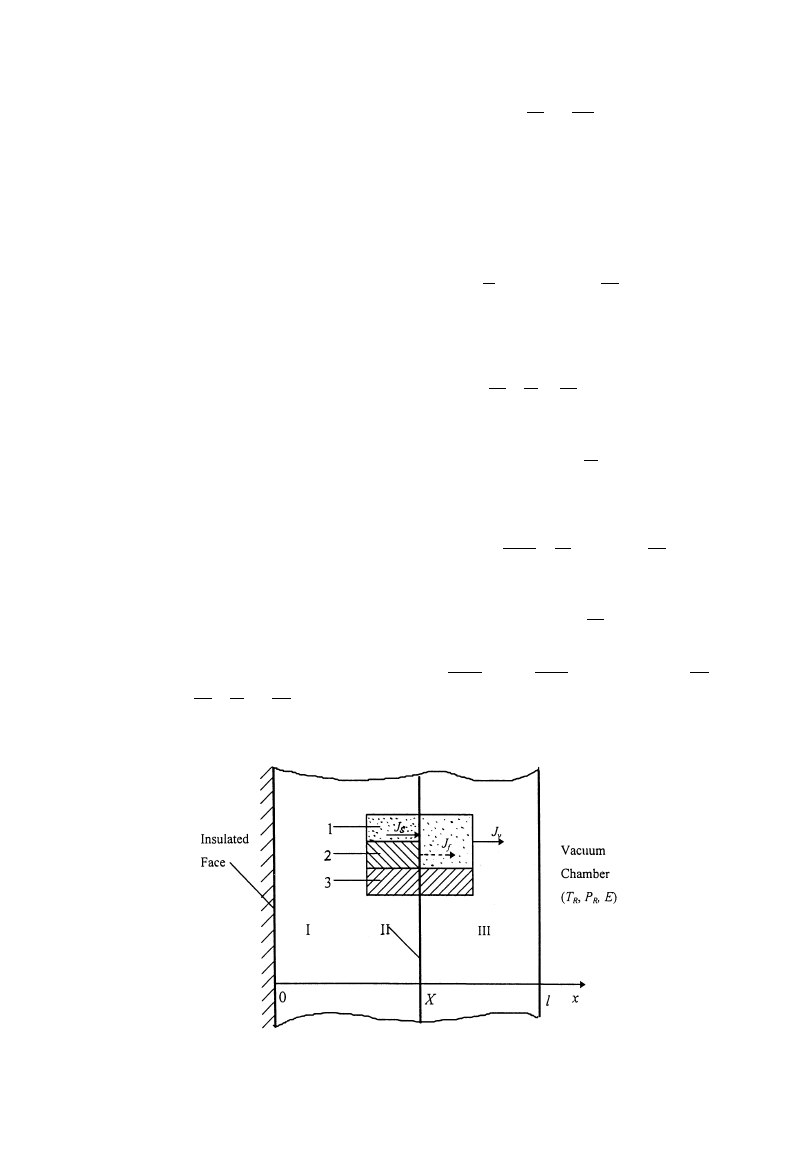
Fig. 1. Physical model of sublimation—condensation. I—Sublimation—condensation region; II—Sublima-

tion front; III-Dried region 1—vapor (

e(1!S)); 2—ice (eS); 3—solid body (1!e).

Based on the volume average theory for heat and

mass transfer in porous media by Whitaker (1977),
this paper developed a sublimation—condensation
model for freeze drying of unsaturated porous media.
The model considered the saturation change in frozen
region, which is called as sublimation—condensation
region in this article. Because the coefficients used in
our model are measurable, it is believed that this
model is more applicable in practice. Numerical simu-
lation of microwave freeze drying of unsaturated por-
ous media was conducted by using the variable time
step finite-difference method. The effects of operating
conditions including electric field strength, sample
thickness and vacuum pressure on the heat and mass
transfer in the sublimation—condensation region and
the drying time of the drying process were primarily
discussed.

MATHEMATICAL MODELING

Figure 1 illustrates an one-dimensional unsaturated

porous medium slab to be freeze-dried with micro-
wave heating. In the environment where the pressure
is below the triple point, the material includes
dried region and sublimation—condensation region
separated by a sublimation front. It is assumed
that water vapor is the only gas in the vacuum
chamber and ideal gas law is applicable. In addition,
the material is considered rigid, homogeneous, and
isotropy.

Dried region

The heat and mass transfer equations in the dried

region can be written as

Mass transfer

e

Lov

Lq

"

L

Lx

A

De

Lov

Lx

B

(1)

Heat transfer

oc

L¹

Lq

"

j

L2¹

Lx2

#

q

(2)

where q is microwave internal heat source.

According to the results of Dyer and Sunderland

(1968), convection heat transfer is neglected in the
energy equation of dried region.

Sublimation-condensation region

The vapor continuity equation can be obtained as

L

Lq

[(1!S)

eov]"!

LJS

Lx

#

I.

(3)

If the heat transfer caused by vapor convection is

neglected, the energy balance equation in sublima-
tion—condensation region changes to

oc

L¹

Lq

"

L

Lx

A

j

L¹

Lx

B

!

I

*H#q

(4)

The vapor source I in this region is defined as

I"!u4!5

LS

Lq

.

(5)

Based on the Darcy’s law and Fick’s law, the vapor

flow in this region can be written as

JS"!

KDKr

kv

ov

LP

Lx

!

(1!S)

eD

Lov

Lx

.

(6)

For saturated vapor of ideal gas, we have

JS"!KS

L¹

Lx

(7)

where

KS"

KDKr

kv

R

o2v#

C

KDKr

kv

R

ov¹#e(1!S)D

D

d

ov

d¹

.

(8)

3190

Z. H. Wang and M. H. Shi

Based on the fact that

eov

u4!5

(

ov

u4!5

;

1

(9)

the following equation can be obtained from eqs (3),
(5), and (7)

I"

e(1!S)

d

ov

d¹

)

L¹

Lq

!

L

Lx

A

KS

L¹

Lx

B

.

(10)

Replacing vapor source I by eq (10), eq. (4) becomes

[

oc]e

L¹

Lq

"

L

Lx

A

je

L¹

Lx

B

#

q

(11)

where

[

oc]e"oc#e(1!S)

d

ov

d¹

*H

(12)

je"j#*HKS.

(13)

Combining eqs (5), (10) and (11), we have

!

u4!5

LS

Lq

"!

L

Lx

A

KS

L¹

Lx

B

#

fT

L

Lx

A

je

L¹

Lx

B

#

fTq

(14)

where

fT"

e(1!S)

[

oc]e

)

d

ov

d¹

.

(15)

Equations (11) and (14) are the equations of heat

and mass transfer in sublimation—condensation re-
gion, respectively.

Sublimation front

If the vapor generated at the sublimation front is

formulated as

Jf"

A

!

u4!5S

dX

d

q

BK

x/X~

(16)

and the vapor flow in dried region is obtained as

Jv"!De

Lov

Lx

(17)

the mass balance equation at the front is

JvDx/X`!JSDx/X~"Jf

(18)

and the energy balance equation is

A

!

je

L¹

Lx

BK

x/X~

!

A

!

j

L¹

Lx

BK

x/X`

"

Jf *H. (19)

In order to quantify the contributions of JSDx/X~

and Jf to the drying rate per unit surface area, a new

parameter fJ is defined as

fJ"

JSDx/X~

JvDx/X`

(20)

where fJ represents the influence of sublimation phe-

nomena in sublimation—condensation region on heat
and mass transfer in the drying process.

Boundary conditions

Due to symmetry of the material, the boundary

condition at the center is

!

je

L¹

Lx

K

x/0

"

0.

(21)

The boundary conditions at the surface are

A

!

j

L¹

Lx

BK

x/l

"

a(¹ Dx/l!¹R)

(22)

ovDx/l"

PR

R¹

Dx/l

.

(23)

Initial conditions

¹

Dr/0"¹0

(24)

S

Dr/0"S0

(25)

X

Dr/0"l.

(26)

NUMERICAL PROCEDURE

The governing equations, eqs (1), (2), (11), (14),

(16)—(19), and (21)—(26) were solved numerically by
using a variable time-step finite-difference method.
A control volume method was used to discretize the
equations uniformly and the grid nodes are located in
the centers of the control volumes as illustrated in
Fig. 2.

The discretization of the equations is given in the

appendix.

In principle, the temperature and ice saturation

profiles in the material can be obtained by solving the
matrix of the algebraic equations. Due to their nonlin-
earity, the temperature and saturation of the sublima-
tion front should be predicted at first in each iteration,
then the algebraic equation groups are solved for the
dried region and sublimation—condensation region
considering the sublimation front as the first kind of
boundary conditions.

In order to reduce the error caused by the explicit

format, a sufficiently fine grid was used. During the
program, test solutions for a typical operation were
obtained by utilizing different grid sizes to check the
grid independence. It was found that the difference of
drying time between the calculations of 200- and
250-grid is less than 0.1%. Thus, the 200-grid was
used in all subsequent computations. At each time

Fig. 2. Schematic for discretization of governing equations.

Sublimation—condensation study during freeze drying

3191

Table 1. Physical properties

Symbol

Value or expression

Unit

Reference

ci

2090

J/(kg °C)

Perry et al. (1992)

cs

1505

J/(kg °C)

calculated from Ma and Peltre

(1975)

D

2.51

]10~5](1.013]105/P)

m

2/s

Perry et al. (1992)

De

78.5

]10~4/(3.4#P/133.3)

m

2/s

Ma and Peltre (1975)

DH

2821500

J/kg

Perry et al. (1992)

KD

4

]10~8/P

m

2

Harper (1962)

Kr

1!S

—

—

u4!5

685

kg/m

3

Experiment

a

6.7

W/(m

2 °C)

Experiment

e

0.75

—

Experiment

ji

2.22

W/(m °C)

Perry et al. (1992)

js

0.2

W/(m °C)

Calculated from Ma and Peltre

(1975)

oi

913

kg/m

3

Perry et al. (1992)

os

320

kg/m

3

Calculated from Ma and Peltre

(1975)

ov

0.1

]exp(!53.7881#0.294552]¹

kg/m

3

Perry et al. (1992)

!

3.987875

]10~4]¹2)

increment, the solution is considered to have achieved
convergence if

K

¹P!¹0P

¹P

K

)

10

~5

(27)

and

K

SP!S0P

SP

K

)

10

~5.

(28)

The physical properties used in the calculation are

listed in Table 1.

The internal heat generation of microwave power

in eqs (2) and (11) is expressed as

q"kE

2

(29)

where k is obtained from Ma and Peltre (1975) for
dried beef and saturated frozen beef. The physical
properties of unsaturated frozen beef, such as dissipa-
tion coefficient, thermal conductivity, density, and
heat capacity, are calculated by volume-average
method.

RESULTS AND DISCUSSION

During microwave freeze drying of unsaturated

porous media, sublimation will take place not only at
sublimation front but also in sublimation—condensa-
tion region. In order to understand the drying mecha-
nism under various operating parameters in practical
freeze-drying process, the effects of those parameters
including electric field strength, vacuum pressure, and
sample thickness on the two kinds of sublimation are
discussed based on numerical calculation results.
A typical condition with initial saturation of S0"0.7

is

used.

The

reference

values

l"0.008 m,

E"120 V/cm, and PR"15 Pa are selected. In the

following calculations, only the parameters having
different values from reference are noted.

Heat and mass transfer in sublimation—condensation
region

Figure 3 shows the distributions of pressure, vapor

density, and saturation in the material at different
times during drying. Figures 3(a) and (b) show that
the pressure and vapor density are of the similar
distributions. It can be seen that both the gradients of
pressure and vapor density in sublimation—condensa-
tion region are large in the initial period, then de-
crease and become less than those in dried region.
Though the gradients are much larger in dried region,
the vapor transfer exists in sublimation—condensation
region as expressed in eq. (6). The situation that the
pressure and vapor density decrease from the material
center to sublimation front as illustrated in Figs 3(a)
and (b) indicates that the vapor will be removed from
sublimation—condensation region. As a result, the ice
in sublimation—condensation region will sublimate
and the saturation in this region will decrease as
shown in Fig. 3(c). It can be seen that the saturation is
nearly in the uniform distribution in sublimation—
condensation region though it is larger near sublima-
tion front than in the center.

All the vapor sublimated in sublimation—condensa-

tion region joins the main flow in dried region. So the
drying rate in microwave freeze drying of saturated
porous media consists of the two flows attributed to
sublimation front and sublimation—condensation re-
gion. Figure 4 shows variation of the two vapor flows,
JSDx/X~ and JvDx/X`, illustrated in Fig. 1, with the

sublimation front at different positions. In fact,
JvDx/X` in the dried region is the drying rate per

unit surface area. JSDx/X~ is the vapor flow sub-

limated in the sublimation—condensation region while
JvDx/X`!JSDx/X~ is the vapor flow JfDx/X~ sub-

limated at the sublimation front. It can be seen
that both JSDx/X~ and JvDx/X` are large when the

3192

Z. H. Wang and M. H. Shi

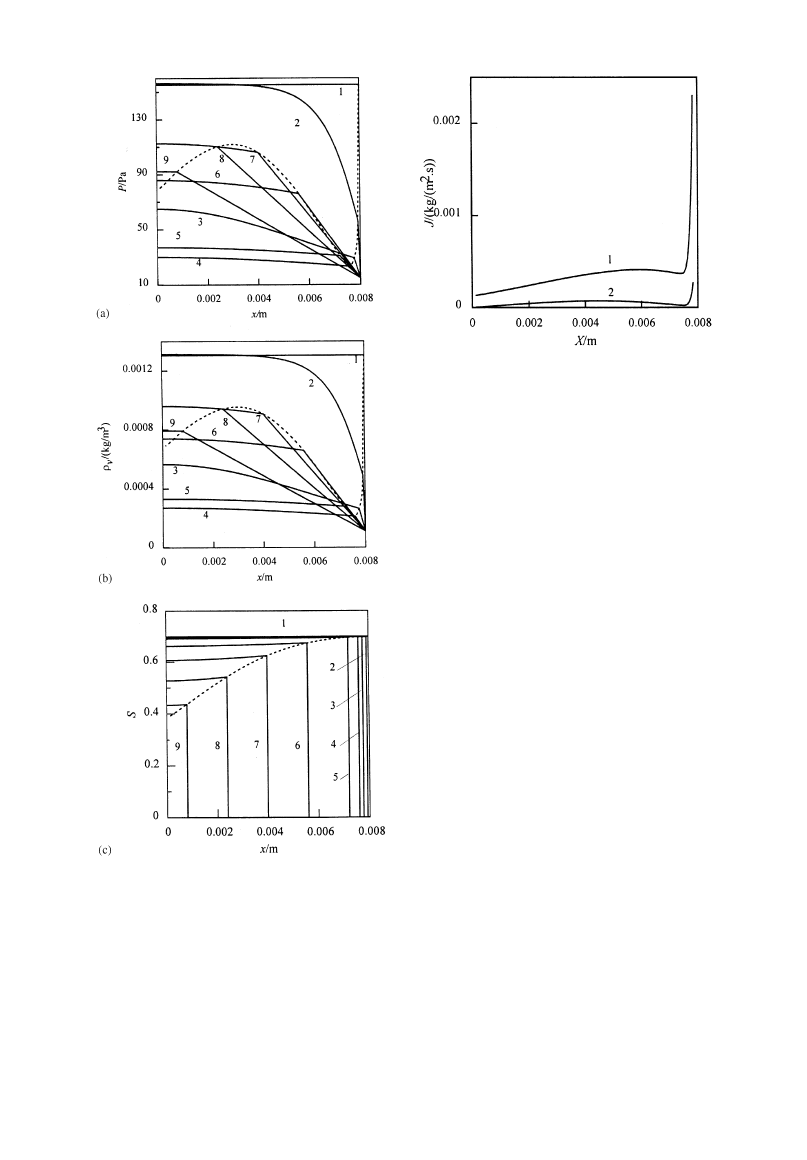
Fig. 3. Profiles of pressure, vapor density, and saturation in
drying

q(s): 1—0; 2—0.1; 3—9; 4—76; 5—572; 6—2714;

7—4950; 8—7489; 9—10434. - - - Sublimation front.

sublimation front is near the surface. This is because
the mass transfer resistance is small in dried region for
the short mass transfer distance and pressure and
vapor density gradients are large in sublimation—con-
densation region when the temperature of sublima-
tion front is approaching wet bulb temperature of the
vacuum chamber at the beginning of drying. When

Fig. 4. Vapor flux at different positions of sublimation front.

1—JvDx/X`; 2—JSDx/X~.

the sublimation front shifts inside, the temperature of
sublimation front approaches wet bulb temperature
rapidly, the temperature distribution of sublimation
region becomes nearly a plateau, and the pressure and
vapor density gradients become small in sublima-
tion—condensation region as illustrated in Figs 3(a)
and (b). So JSDx/X~ decreases as shown in Fig. 4. In

the mean time, due to the increase of the mass transfer
resistance and the coupled effect of temperature,
JvDx/X` decreases. After the two flows pass the

smallest values in the initial period, they will increase
with the drying process. Then JvDx/X` becomes small-

er after X"0.0059 m while JSDx/X~ decreases after

X"0.0045 m.

Electric field strength

Effects on heat and mass transfer. Figure 5 illus-

trates the effect of electric field strength on fJ at

different sublimation front positions. It can be seen
that the curves are in the similar shape but fJ increases

with increasing electric field strength, E. As the elec-
tric field strength increases, the sublimation-conden-
sation region absorbs more energy and the average
temperature and temperature difference also increase.
Based on eq. (8), KS will increase exponentially with

the temperature in sublimation—condensation region,
resulting in the large vapor flow. There are significant
differences of fJ for different electric field strengths.

For example, the maximum fJ is 0.14 at E"100 V/cm

while 0.33 at E"175 V/cm except the initial period.
The sublimation will reduce the temperature differ-
ence in the sublimation—condensation region. This
means a more homogeneous heating in the sample
can be achieved and the probability of ice melting in
the frozen region of the material would be reduced at
higher electric field strength.

Due to the effect of electric field strength on vapor

transport, the sublimation phenomenon in sublima-
tion—condensation region is influenced by different

Sublimation—condensation study during freeze drying

3193

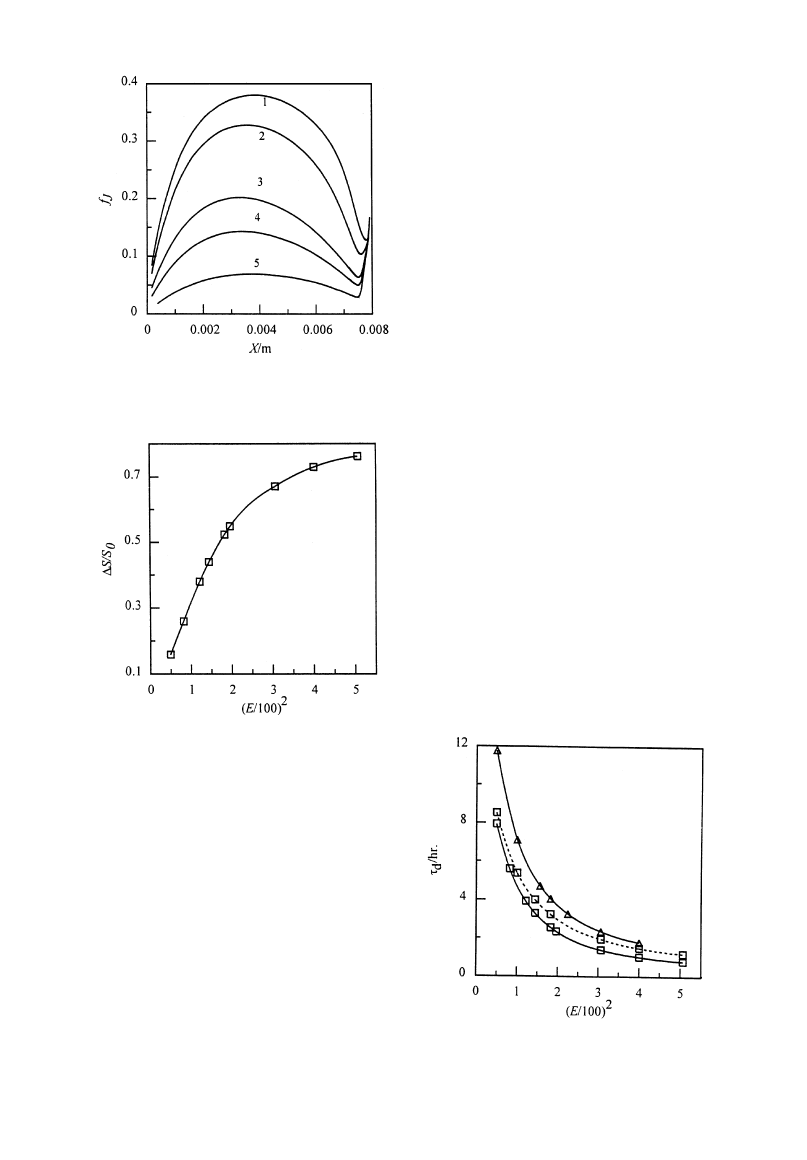
Fig. 5. Variation of fJ at different positions of sublimation

front E(V cm

~1); 1—225; 2—175; 3—120; 4—100; 5—70.

Fig. 6. Effects of E on sublimation—condensation region.

electric field strengths. Saturation change of sublima-
tion—condensation region for a complete drying pro-
cess is presented to illustrate the effect of electric field.
The calculation shows that the saturation distribution
in the sublimation—condensation region is a plateau
as shown in Fig. 3(c). Accordingly, the saturation of
sublimation front is applied to represent the satura-
tion variation of sublimation—condensation region
during the drying process. Figure 6 (in which,
*S"S0!S%/$) shows the relative difference of subli-

mation front saturation for the complete drying pro-
cess at different electric field strengths. The square of
electric field strength is used in abscissa axis of the
figure since the internal heat generation or the
strength of absorbed energy is in a square function of
electric field strength, E. The figure indicates that
a larger E value will cause a larger saturation change
of sublimation front. For example,

*S/S0 is about

44% for E"120 V/cm and 73% for E"200 V/cm. It
seems that increasing rate of

*S/S0 with (E/100)2 is

larger for lower electric field strength. The calculation
proves that melting phenomenon occurs ('!3°C)
when E*250 V/cm.

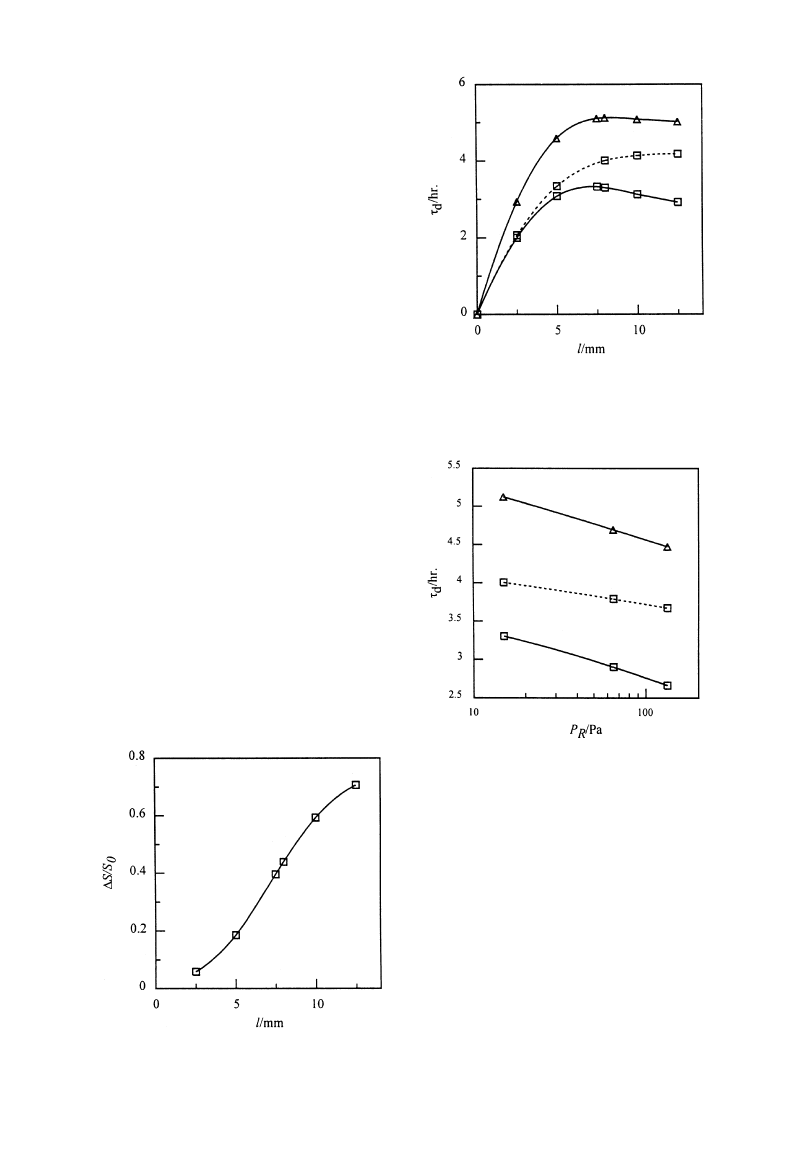
Effects on drying time. Figure 7 shows the drying

times at different electric field strengths under the
drying conditions of S0"0.7 and S0"1. In order to

study the effects of sublimation in sublimation—con-
densation region, the drying processes at S0"0.7 are

calculated by the sublimation interface model which
considers sublimation only at interface. The calcu-
lation results show that the difference of drying
time increases with E between the sublimation—
condensation and sublimation interface models. It
indicates that the influence of sublimation—condensa-
tion region on drying process is more significant for
larger E. This demonstrates that the sublimation—
condensation model is more applicable for practical
drying process.

Though no sublimation—condensation region exists

for saturated materials, the variation of drying time is
different from unsaturated materials. Simulation re-
sults show that drying time decreases with increasing
electric field strength for both initial saturation condi-
tions. However, the drying rates are different at differ-
ent S0. The drying times calculated from sublima-

tion—condensation model was used for S0"0.7. It

was observed that the ratio of the drying time at
S0"1 to that at S0"0.7 is about 1.48 for

E"70 V/cm and 2.0 for E"200 V/cm. As a result,
the advantage of using lower initial saturation is obvi-
ous for higher electric field strength. Unfortunately,
the melting phenomena occur at higher E value. The
calculation also shows that the critical E value of
melting is higher for lower S0. For example, the criti-

cal E value is about 225 V/cm for S0"1 while

Fig. 7. Effects of sublimation—condensation region on drying
time. (—) Sublimation—condensation model; (- - -) sublima-

tion interface model. S0: (K) 0.7; (n) 1.

3194

Z. H. Wang and M. H. Shi

250 V/cm for S0"0.7. Figure 7 also shows that de-

creasing rate of drying time becomes smaller when
electric field is strong, this means that the too large
electric field strength is not necessary for microwave
freeze drying.

Sample thickness

Effects on heat and mass transfer. The calculations

show that more energy is absorbed by thicker samples
at a given electric field strength. On the other hand,
mass transfer resistance is greater for thicker samples.
Figure 8 shows the variation of

*S/S0 with half

sample thickness. In case of large sample thickness,
the influence of vapor sublimated from the sublima-
tion—condensation region is obvious, therefore the
saturation change of the sublimation—condensation
region is large. The figure also shows that

*S/S0

changes linearly with sample thickness and the change
rate is the largest in the range of l from 5 to 10 mm.
Thus, the

*S/S0 vs l plot is an ‘S’-shaped curve.

Effects on drying time. In order to compare the

effects of sublimation—condensation region on drying
process at different sample thicknesses, the calculated
drying times at S0"0.7 are illustrated in Fig. 9 from

sublimation interface and sublimation—condensation
models, respectively. It can be seen that the influence
of sublimation—condensation region on drying time
becomes more significant when sample thickness in-
creases. This indicates that the sublimation—conden-
sation region cannot be neglected in microwave freeze
drying of unsaturated porous media, especially for
larger scale samples. The drying time of saturated
material is also calculated for different sample
thicknesses as shown in Fig. 9. It shows that drying
time increases dramatically with sample thickness
increasing at 0 mm for both initial saturation condi-
tions. The drying times are almost independent of
sample thickness in case of l'5 mm. This is because

Fig. 8. Effects of half sample thickness on sublimation—con-

densation region.

Fig. 9. Effects of sublimation—condensation region on dry-
ing time. (—) Sublimation—condensation model; (- - -) subli-

mation interface model. S0: (K) 0.7; (n) 1.

Fig. 10. Effects of sublimation—condensation region on dry-
ing time. (—) Sublimation—condensation model; (- - -) subli-

mation interface model. S0: (K) 0.7; (n) 1.

the surface effects are more significant for thinner
sample.

The

melting

phenomena

occur

when

l'12.5 mm for S0"1, while l'15 mm for S0"0.7.

»

acuum pressure

Effects on heat and mass transfer. The sublimation—

condensation phenomena of unsaturated porous me-
dia were numerically studied at three vacuum pres-
sures. The calculation shows that the maximum

fJ increases from 0.2 at PR"15 Pa to 0.31 at

PR"133 Pa. This is because high vacuum pressure

causes high wet bulb temperature and high vapor
transfer resistance in the dried region, so the temper-
ature and vapor flow in sublimation—condensation

Sublimation—condensation study during freeze drying

3195

region are high. The numerical results also indicate
that

*S/S0 increases from 0.44 at PR"15Pa to 0.64 at

133 Pa. This means that higher vacuum pressure
causes greater effect on sublimation—condensation re-
gion and will produce greater effect on drying time.

Effects on drying time. Figure 10 shows the vari-

ation of drying time with vacuum pressure calculated
from sublimation interface model and sublima-
tion—condensation model. It can be seen that the
difference between the two models becomes larger
with increasing PR. However, high vacuum pressure

should be avoided in practical microwave freeze-dry-
ing operations because of melting and gas discharge.
The figure also shows the drying times at different
vacuum pressures and S0"1. It shows that the dry-

ing times decrease with increasing vacuum pressure at
both S0"0.7 and S0"1. Nevertheless, the effects of

vacuum pressure on drying process is not very signifi-
cant since the variation range of PR discussed here is

in the same order of magnitude.

CONCLUSIONS

The numerical calculations show that the sublima-

tion—condensation region plays an important role
in microwave freeze drying of unsaturated porous
media and the effects of sublimation—condensation
phenomena on drying process depend on operation
parameters. For larger electric field strength, vapor
transfer in sublimation—condensation region is more
intensive and larger part of the vapor is sublimated
from this region, so the effect of sublimation—conden-
sation region on drying time is more significant.
Smaller initial saturation is beneficial at higher elec-
tric field strength. However, too large electric field
strength is not necessary for microwave freeze drying.
In case of larger sample thickness, the saturation
change of the sublimation—condensation region is
larger, and the effect of sublimation—condensation
region on drying time is more significant. So sublima-
tion—condensation region cannot be neglected in
microwave freeze drying of unsaturated porous me-
dia, especially for larger scale samples. Though the
effect of vacuum pressure on sublimation—condensa-
tion region is significant a little more for higher vac-
uum pressure, the effect of sublimation—condensation
region on drying time is not so significant in the
observed range.

NOTATION

c

specific heat of the material, J/(kg °C)

D

diffusivity, m

2/s

De

effective diffusivity, m

2/s

E

electric field peak strength, V/cm

fT

source conversion coefficient from heat to
mass, kg/J

fJ

ratio of the vapor flux sublimated from sub-
limation—condensation region to the vapor
flux in dried region

*H

latent heat of sublimation, J/kg

J

mass flux, kg/(m

2 s)

Jf

mass flux of vapor sublimated at sublima-
tion front, kg/(m

2 s)

JS

mass flux of vapor in sublimation—conden-
sation region, kg/(m

2 s)

Jv

mass flux of vapor in dried region, kg/(m

2 s)

k

dissipation coefficient defined by eq. (29),
J/(s m

3) (V/cm)~2

KD

permeability of the dry material, m

2

Kr

relative permeability

KS

effective coefficient of nonisothermal vapor
motion in sublimation—condensation re-
gion, kg/(m s °C)

l

sample half thickness, m

P

pressure, Pa

PR

vacuum pressure, Pa

q

density of microwave power absorbed,
J/(s m

3)

R

water vapor gas constant, m

2/(s2 °C)

S

saturation of ice in sublimation—condensa-
tion region

¹

temperature, °C

u4!5

moisture content of the saturated porous
medium, kg/m

3

x

space coordinate, m

X

position of sublimation front, m

Greek letters
a

heat transfer coefficient, J/(s m

2 °C)

e

porosity

j

thermal conductivity, J/(s m °C)

k

viscosity, kg/(m s)

o

density, kg/m

3

q

time, s

qd

drying time, hr

Subscripts
0

initial value

d

of dried sample

D

in the dried region

i

ice

s

solid body

S

in sublimation—condensation region

v

vapor

Superscript
0

previous time step

REFERENCES

Ang, T. K., Ford, J. D. and Pei, D. C. T. (1977)

Microwave freeze-drying of food: a theoretical in-
vestigation. Int. J. Heat Mass ¹ransfer 20, 517—526.

Dyer, D. F. and Sunderland, J. E. (1967) The transient

temperature distribution during sublimation dehy-
dration. ASME J. Heat ¹ransfer 89, 109—110.

Dyer, D. F. and Sunderland J. E. (1968) The role of

convection in drying. Chem. Engng Sci. 23, 965—970.

Fey, Y. C. and Boles, M. A. (1987a) An analytical

study of the effect of convection heat transfer on the
sublimation of a frozen semi-infinite porous me-
dium. Int. J. Heat Mass ¹ransfer 30, 771—779.

3196

Z. H. Wang and M. H. Shi

Fey, Y. C. and Boles, M. A. (1987b) An analytical

study of the effect of the Darcy and Fick laws on the
sublimation of a frozen porous medium. ASME J.
Heat ¹ransfer 109, 1045—1048.

Fey, Y. C. and Boles M. A. (1988) Analytical study of

vacuum-sublimation in an initially partially filled
frozen porous medium with recondensation. Int. J.
Heat Mass ¹ransfer 31, 1645—1653.

Fox, E. C. and Thomson, W. J. (1972) Coupled heat

and mass transport in unsteady sublimation drying.
A.I.Ch.E. J. 18, 792—797.

Harper, J. C. (1962) Transport properties of gases in

porous media at reduced pressure with reference of
freeze-drying. A.I.Ch.E. J. 8, 298—302.

King, C. J., Lam, W. K. and Sandall, O. C. (1968)

Physical properties important for freeze-drying
poultry meat. Food ¹echnol. 22, 1302—1308.

Lin, S. (1981) An exact solution of the sublimation

problem in a porous medium. ASME J. Heat
¹

ransfer 103, 165—168.

Lin, S. (1982) An exact solution of the sublimation

problem in a porous medium. Part II—with an
unknown temperature and vapor concentration at
the moving sublimation front. ASME J. Heat
¹

ransfer 104, 808—811.

Luikov, A. V. (1975) Systems of differential equations

of heat and mass transfer in capillary-porous bodies
(Review). Int. J. Heat Mass ¹ransfer 18, 1—14.

Lusk, G., Karel, M. and Goldblith, S. A. (1964) Ther-

mal conductivity of some freeze-dried fish. Food
¹

echnol. 18, 1625—1628.

Ma, Y. H. and Peltre, P. (1975) Freeze dehydration by

microwave energy: Part I. theoretical investigation.
A.I.Ch.E. J. 21, 335—344.

Massey, W. M. Jr and Sunderland, J. E. (1967)

Measurement of thermal conductivity during
freeze-drying of beef. Food ¹echnol. 21, 408—412.

Patankar, S. V. (1980) Numerical Heat ¹ransfer and

Fluid Flow. Hemisphere, New York, U.S.A.

Perry, H. R., Green, D. and Maloney, J. O. (1992)

Perry’s Chemical Engineering Handbook, 6th Edn.
McGraw-Hill, New York, U.S.A.

Whitaker, S. (1977) Simultaneous heat, mass, and

momentum transfer in porous media: A theory of
drying. In Advances in Heat ¹ransfer, Vol. 13, pp.
119—203. Academic Press, New York, U.S.A.

APPENDIX

Equations (2) and (11) are in the same form of nonlinear

heat conduction equation with internal heat generation.
They can be expressed in the following implicit finite-differ-
ence format:

aP¹P"aE¹E#aW¹W#b

(A1)

where aP, aE, aW, are the coefficient matrix and b is the

source term, which are determined as in Patankar (1980).

By applying implicit format, eq. (14) is discretized as

SP"S0P#

*q

um

GC

(KS)e

*x

(¹E!¹P)!

(KS)w

*x

(¹P!¹W)

D

1

*x

H

!

*q

um

G

( fT)P

C

(

je)e

*x

(¹E!¹P)!

(

je)w

*x

(¹P!¹W)

D

1

*x

#

( fT)PqP

H

(A2)

where S

0P represents the value of SP of previous time step, and

the transport properties are obtained by arithmetic mean

(KS)e"

2(KS)E(KS)P

(KS)E#(KS)P

.

(A3)

(KS)w, (je)e, and (je)w are approximated in similar expres-

sions. According to the previous work (Ma and Peltre, 1975;
Ang et al., 1977), the vapor concentration in the dried region
is approximately in linear distribution. Therefore, eq. (1) can
be written in the following form:

Jv"!Dea

ovDx/l!ovDx/X

l!X

(A4)

where Dea is determined as

Dea"

(De)n#(De)N

X

2

.

(A5)

Based on eqs (18) and (19), the following equation of

energy balance at sublimation front is obtained:

C

Jv!

A

!

KS

L¹

Lx

BK

x/X~

D

*H"

A

!

je

L¹

Lx

BK

x/X~

!

A

!

j

L¹

Lx

BK

x/X`

.

(A6)

After discretization, it is replaced by

C

Jv#(KS)N

X~1@2

¹N

X

!¹N

X~1

*x

D

*H"!(je)N

X~1@2

¹N

X

!¹N

X~1

*x

#

(

j)N

X`1@2

¹N

X~1

!¹N

X

*x

(A7)

where (KS)N

X~1@2

, (

je)N

X~1@2

, and (

je)N

X~1@2

are calculated using

a formula similar to eq. (A3).

The finite-difference expression of SN

X

can be got in explicit

form by replacing the temperature and physical properties in
eq. (A2) with the corresponding values of previous time step.

The boundary conditions, eqs (21)— (23), can be discre-

tized as

¹1!¹2"

0

(A8)

!

jn

~1@2

¹n!¹n~1

*x

"

a(¹n!¹R)

(A9)

ovn"

PR

R¹n

(A10)

where

jn

~1@2

"

2

jnjn~1

jn#jn~1

.

(A11)

Since the complexity of the sublimation front, of which

temperature and saturation are intensively nonlinear func-
tions of time during microwave freeze drying, an explicit
method is employed to determine the time step of each
iteration as follows:

*q"!

*xum(SN

X~1

)

0

(Jf)0

(A12)

where

(Jf)0"(Jv)0!(JS)0

(A13)

(JS)0"!(KS)(¹)0N

0X

~

Ç

@

È

(¹)

0N

0X

!

(¹)

0N

0X

~

Ç

*x

(A14)

N

0X"NX#1

(A15)

and (KS)0N

0X

~1@2

is obtained by arithmetic mean similar to eq.

(A3).

Sublimation—condensation study during freeze drying

3197