Spis treści

Interpolacja

 

 

 

PODSTAWY METOD NUMERYCZNYCH

 

 

Metody numeryczne jest to dział nauki zajmujący się rozwiązywaniem różnych zagadnień matematycznych za pomocą komputera. Podczas reprezentacji komputerowej dochodzi do wielu uproszczeń ponieważ nie każda liczba jest reprezentowana - nie istnieje pojęcie nieskończoności, dowolnie dużej dokładności, powstają luki („gaps”) w reprezentacji liczb rzeczywistych.

 

Źródła błędów w czasie obliczeń:

 

1. Błąd danych wejściowych - każdy pomiar jest zaokrąglony

2. Błędy zaokrągleń w czasie obliczeń

3. Błąd obcięcia błędy zaokrągleń w czasie obliczeń

 

Reprezentacja liczby e^x jako rozwinięcie w szereg:

 

 

 

 

Liczby w komputerze zapisujemy w reprezentacji zmiennopozycyjnej:

 

x - liczba rzeczywista, znormalizowana reprezentacja dziesiętna:

 

x=sთmთ2^C gdzie: |m|=0.1...1

 

Znormalizowana reprezentacja dwójkowa:

 

x=sთmთ2^C |m|=0.5...1

 

gdzie : s - znak, m - mantysa (część ułamkowa), c - cecha (część całkowita)

 

Na zapis liczby poświęcamy odpowiednią liczbę bitów, przy czym:

 

• -         za dokładność zapisu odpowiada mantysa - im większą pamięć jej poświęcimy dostaniemy dokładniejszą reprezentację

• -         za zakres zapisu odpowiada cecha - zwiększenie ilości bitów na cechę odpowiada zwiększenie zakresu reprezenatacj

 

Przyjmijmy, że przeznaczmy na zapis liczby d bitów pamięci. Na mantysę przeznaczamy t bitów, natomiast na zapis cechy d-t-1 bitów (jeden bit odejmujemy na znak)

 

Ponieważ maksymalna cecha c­_max­­­­ = -c _min= 2^d-t-1, a mantysa m_t należy do przedziału <1/2, 1)

reprezentowane są liczby spełniające warunek:

 

Wynika z tego, iż liczby będące poza tym zakresem nie mogą być zapisane w naszym systemie

Pojawia się problem niedoboru i nadmiaru:

• -         dla liczb, których cecha < c_min - niedobór

• -         dla liczb, których cecha c>c_max - nadmiar

 

Reprezentacja zmiennopozycyjna jest uniwersalna, natomiast gdy chcemy operować na liczbach całkowitych

możemy stosować reprezentację stałopozycyjną:

a - liczba całkowita, na zapis przeznaczamy d bitów pamięci

zakres liczb reprezentowanych a należy do przedziału <-2^d+1,2^d-1>

Przy reprezentacji stałopozycyjnej mamy pewność dokładności wykonywanych działań

 

 

 

 

 

Wstępne wiadomości

Strona główna

Aproksymacyjna

 

 

INTERPOLACJA

 

Zadaniem interpolacji jest utworzenie funkcji, która przebiega przez zadane punkty. Stosuje się różne klasy funkcji do interpolowania - wielomiany algebraiczne, funkcje sklejane, funkcje trygonometryczne.

 

Zadanie interpolacji możemy sformułować następująco:

W przedziale [a,b] mamy danych n+1 różnych punktów x₀,x₁,...,x_n (węzły interpolacji) oraz wartości funkcji y=f(x) w tych punktach f(x₀)=y₀,f(x₁)=y₁,...,f(x_n)=y_n . Znaleźć funkcję F(x), która w węzłach interpolacji ma te same wartości co f(x) i przybliża f(x) w punktach.

 

 

1. I.                Interpolacja wielomianowa:

 

Twierdzenie

Istnieje dokładnie jeden wielomian interpolacyjny stopnia co najwyżej n (nႳ0), który w punktach x₀, x₁,...,x_n przyjmuje wartości y₀,y₁,...,y_n

 

Wzór Lagrange'a

x₀, x₁,...,x_n - zadany zbiór punktów

y₀,y₁,...,y_n - zadane wartości funkcji w punktach

 

oznaczmy W_n+1=(x-x₀)(x-x₁)...(x-x_n)

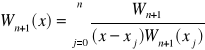
- jest to wzór interpolacyjny Lagrange'a, podstawiając do

niego zadane wartości otrzymujemy wzór wielomianu przechodzącego przez zadane punkty

 

 

 

 

2. II.             Interpolacja funkcjami sklejanymi

 

Interpolacja funkcjami sklejanymi polega na „łączeniu punktów”, w każdym odcinku przybliżamy funkcję wielomianem ustalonego (niskiego) stopnia, tak aby funkcja przybliżająca była ciągła wraz z pochodnymi na przedziale interpolacji [a,b]

 

Interpolacja funkcjami sklejanymi stopnia pierwszego

 

Załóżmy, że dysponujemy zbiorem n+1 węzłów interpolacji wraz z wartościami funkcji

(x₀,y₀), (x₁,y₁), ..., (x_n,y_n). W przypadku wielomianowych metod interpolacji może się zdarzyć,

że charakter interpolowanej funkcji uniemożliwia dobre odwzorowanie za pomocą

wielomianu interpolującego. Możemy w takich przypadkach spróbować zastosować liniową

interpolację pomiędzy poszczególnymi węzłami:

 

 

s_k(x)=y_k+d_k(x-x_k) gdzie

 

W ten sposób otrzymamy zestaw funkcji interpolujących przebieg pomiędzy węzłami

dzielącymi przedział interpolacji na podprzedziały. Sklejając te funkcje razem otrzymamy

funkcję interpolującą następującej postaci:

Można zwrócić uwagę na to, że pochodna funkcji s(x) jest nieciągła we wszystkich punktach

x_k dla k=1,...,n-1

 

 

 

 

Interpolacja

Strona główna

Równania różniczkowe

 

APROKSYMACJA

 

 

Zadaniem aproksymacji jest przybliżenie funkcji F(x) (albo tablicy charakteryzujących funkcję) funkcją f(x) tak aby była ona do niej najbardziej podobna.

 

F(x) - znana funkcja lub określona tablica

f(x) - funkcja aproksymująca

Przybliżenie obarczone jest błędem aproksymacji.

 

Aproksymacja liniowa

 

X - przestrzeń liniowa unormowana (skończenie lub nieskończenie wymiarowa)

F(x)჎ X - funkcja aproksymująca X_n - n wymiarowa podprzestrzeń przestrzeni X

 

Aproksymacja funkcji F(x) polega na wyznaczeniu takich współczynników a₀,a₁,...,a_n funkcji:

f(x)= a₀ၪ₀(x)+ a₁ၪ₁(x)+….+ a_nၪ_n(x)

gdzie: ၪ₀,ၪ₁,…,ၪ_n są funkcjami bazowymi n+1 wymiarowej podprzestrzeni liniowej X_n+1, aby f(x) spełniała pewne warunki np. minimalizowała normę różnicy | f(x) - F(x) |

 

Aproksymacja wymierna

 

gdzie ၪ_i(x), ၹ_i(x) są elementami tej samej bazy k-wymiarowej podprzestrzeni liniowej k=max(n,m), zaś a_i,b_i są stałymi współczynnikami, które należy wyznaczyć.

 

W aproksymacji liniowej należy określić:

- odpowiednią podprzestrzeń liniową X_n i związaną bazę

- odpowiednią miarę.

 

Wybór podprzestrzeni:

 

Jeśli funkcja F(x) jest ciągła na przedziale (a,b) (F(x)჎C(a,b)) to funkcje ၪ_k(x) będą elementami pewnej n+1 wymiarowej podprzestrzeni C(a,b).

 

1. Jeśli F(x) jest okresowa, to przydatna jest podprzestrzeń funkcji trygonometrycznych z bazą:

1, sinx, cosx, sin2x, cos2x, ..., sinkx, coskx

 

2. Podprzestrzeń wielomianów - stopnia co najwyżej n z bazą jednomianów :

1, x, x²,..., xⁿ lub bazą wielomianów Czebyszewa T₀(x),T₁(x), T₂(x),..., T_n(x)

- funkcje bazowe mało wrażliwe na błędy

3. Można też użyć bazy wielomianów Lagrange'a

 

 

 

Aproksymacja

Strona główna

Przykłady w Mathcadzie

 

RÓWNANIA RÓŻNICZKOWE

 

Równania rzędu pierwszego

 

Równanie różniczkowe rzędu pierwszego ma postać y'=f(x,y)

Równanie to posiada nieskończenie wiele rozwiązań różniących się stałą.

Rozwiązanie możemy ustalić mając dany warunek początkowy Cauchy'ego.

 

Metoda uzyskiwania rozwiązanie szczególnego

 

Dane:

warunek początkowy f₀=(x₀,y₀)

znając funkcję f(x,y) można obliczyć wartość pochodnej w punkcie początkowym

p₀=f(x₀,y₀)თdy/dx - współczynnik kierunkowy w punkcie A₀( prosta A₀T₀).

Przybliżamy na odcinku h krzywą przy pomocy prostej stycznej i wyznaczamy punkt N1 jako przybliżoną wartość y₁ (zamiast punktu M1);

y₁=y₀+၄y ၄y=p₀თh=hთf(x₀,y₀)

Startując z N1 obliczamy następną przybliżoną wartość y₂ w punkcie N2.

Stabilizujemy wartości y(x) w punktach x₀,x₁,...,x_n - jest to metoda Eulera - metoda stycznych.

 

Źródła błędów podczas rozwiązywania - błąd metody i błąd zaokrągleń.

 

II. Aproksymacja krzywej nie prostą lecz łukiem paraboli.

 

Wykorzystywane są 2 właściwości (słuszne dla paraboli)

1. Styczna do łuku M₀M₁ w punkcie p₀ odciętej będącej średnią arytmetyczną odciętych punktów M₀ i M₁ jest równoległa do odcinka M₀M₁.

 

Zmodyfikowana metoda Eulera

Gdyby znany był punkt P o odciętej (x₀+x₁)/2 to wystarczyłoby obliczyć styczną w P i poprowadzić równoległą M₀M₁ (M₁ punkt przecięcia równoległy z prostą x=x₀+h.

Punkt P aproksymujemy P` - współczynnik kierunkowy

P`={x`=x₀+h/2 y`=y<sub>0</sub>+h/2∙p<sub>0</sub>} p<sub>0</sub>=f`(x₀,y₀); x`,y` - nowe punkty

tg kąta nachylenia stycznej oraz odcinka M₀M₁

 

Współrzędne punktu M1 {x₁=x₀+h y₁=y₀+h∙p`}

 

Formuły te można zapisać:

k1=h∙f(x₀,y₀) k2=h∙f(x₀+h/2,y₀+k1/2)

y₁=y₀+k2, potem wyznacza się współrzędne M2 (x₀+2∙h) korzystając z M1 itd.

y_i+1=y_i+h∙f(x_i+1/2∙h,y_i+1/2∙h∙f(xi,y_i)

Metoda Rungego-Kutty

 

Szukamy współczynników: a,b,..., ၡ,ß,ၸ,.. oraz liczb R₁,R₂,.. takich aby wartość y określona przez ciąg równań była możliwie blisko dokładnej wartości

 

k1=hთf(x₀,y₀); k2=hთf(x₀+aთh,y₀+ၡთk1)

k3=hთf(x₀ + bთh, y₀+ßთk1+ၸთk2) itd.

y₁=y₀+R₁თk1+…+Rnთkn+…

 

Formuły drugiego rzędu:

k1=hთf(x₀,y₀) k2=hთf(x₀+aთh,y₀+ၡთk1)

y₁=y₀+R₁k1+R₂k2

 

To przybliżenie i przybliżenie wzorem Taylora powinno różnić się jak najmniej.

 

Wyprowadzenie: R₁,R₂,ၡ,a

 

y(x) spełnia y`(x)=f(x,y(x)), zróżniczkujmy względem x y``(x)=f`x+y`თf`y

 

 

 

 

Obszerniejszy material na temat równań różniczkowych mozna znalesc tutaj

---