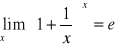WYKŁAD 2 GRANICA FUNKCJI I CIĄGŁOŚĆ FUNKCJI

POJĘCIA WSTĘPNE

Def. 3.1 (otoczenie punktu)

Otoczeniem o promieniu
punktu
nazywamy zbiór
.

Gdy X=R, to jako otoczenie punktu
o promieniu r przyjmujemy przedział
.

Def. 3.2 (sąsiedztwo punktu)

Sąsiedztwem o promieniu
punktu
nazywamy zbiór
.

Gdy X=R, to jako sąsiedztwo punktu
o promieniu r przyjmujemy sumę przedziałów
.

Def. 3.3 (punkt skupienia zbioru)

Punkt
nazywamy punktem skupienia zbioru
wtedy i tylko wtedy, gdy do każdego otoczenia
należy co najmniej jeden różny od
punkt
.

GRANICA FUNKCJI (GRANICA WŁAŚCIWA)

Niech będzie dana funkcja
,
oraz niech
będzie punktem skupienia dziedziny funkcji
.

Def. 3.4 (Heinego granicy właściwej funkcji w punkcie)

Liczbę g nazywamy granicą właściwą funkcji f w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

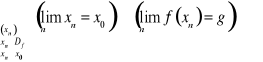
Def. 3.5 (Cauchy'ego granicy właściwej funkcji w punkcie)

Liczbę g nazywamy granicą właściwą funkcji f w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

GRANICE JEDNOSTRONNE FUNKCJI

Def. 3.6 (Heinego granicy lewostronnej właściwej funkcji w punkcie)

Niech będzie dana funkcja
,
oraz niech
będzie punktem skupienia zbioru
. Liczbę g nazywamy granicą właściwą lewostronną funkcji f w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

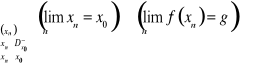
Uwaga. Definicja Heinego granicy prawostronnej funkcji w punkcie jest analogiczna. Oznaczamy ją symbolem
.

Def. 3.7 (Cauchy'ego granicy lewostronnej właściwej funkcji w punkcie)

Niech będzie dana funkcja
,
oraz niech
będzie punktem skupienia zbioru
. Liczbę g nazywamy granicą lewostronną właściwą funkcji f w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

Uwaga. Definicja Cauchy'ego granicy prawostronnej funkcji w punkcie jest analogiczna.

GRANICE NIEWŁAŚCIWE FUNKCJI

Def. 3.8 (Heinego granicy niewłaściwej funkcji w punkcie)

Niech będzie dana funkcja
,
oraz niech
będzie punktem skupienia zbioru
. Funkcja f ma granicę niewłaściwą w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

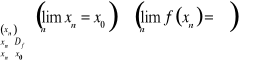
Uwaga. Definicja Heinego granicy niewłaściwej -∞ funkcji w punkcie jest analogiczna do definicji podanej powyżej.

Def. 3.9 (Cauchy'ego granicy niewłaściwej funkcji w punkcie)

Niech będzie dana funkcja
,
oraz niech
będzie punktem skupienia zbioru
. Funkcja f ma granicę niewłaściwą w punkcie x₀, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

Uwaga. Definicja Cauchy'ego granicy niewłaściwej -∞ funkcji w punkcie jest analogiczna do definicji podanej powyżej.

Tw. 3.10 (warunek konieczny i wystarczający istnienia granicy)

Funkcja f ma w punkcie x₀ granicę właściwą (lub niewłaściwą) wtedy i tylko wtedy, gdy

.

Wspólna wartość granic jednostronnych jest równa granicy funkcji.

GRANICE FUNKCJI W NIESKOŃCZONOŚCI

Def. 3.11 (Heinego granicy właściwej funkcji w nieskończoności)

Niech funkcja f będzie określona na przedziale (a,∞), -∞ ≤ a < ∞. Liczba g jest granicą właściwą funkcji f w ∞, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

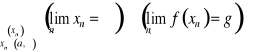
Uwaga. Definicja Heinego granicy właściwej funkcji w -∞ jest analogiczna do definicji podanej powyżej.

Def. 3.12 (Cauchy'ego granicy właściwej w nieskończoności)

Niech funkcja f będzie określona na przedziale (a,∞), -∞ ≤ a < ∞. Liczba g jest granicą właściwą funkcji f w ∞, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

Uwaga. Definicja Cauchy'ego granicy właściwej w -∞ jest analogiczna do definicji podanej powyżej.

Def. 3.13 (Heinego granicy niewłaściwej funkcji w nieskończoności)

Niech funkcja f będzie określona na przedziale (a,∞), -∞ ≤ a < ∞. Funkcja f ma w ∞ granicę niewłaściwą ∞, co zapisujemy

,

wtedy i tylko wtedy, gdy

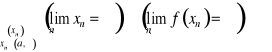
Def. 3.14 (Cauchy'ego granicy niewłaściwej funkcji w nieskończoności)

Niech funkcja f będzie określona na przedziale (a,∞), -∞ ≤ a < ∞. Funkcja f ma w ∞ granicę niewłaściwą ∞, co zapisujemy

,

wtedy i tylko wtedy, gdy

.

Tw. 3.15 (o równoważności definicji granic funkcji)

Odpowiadające sobie definicje Heinego i Cauchy'ego granic funkcji są równoważne.

TWIERDZENIA O GRANICACH FUNKCJI

Tw. 3.16 (o arytmetyce granic funkcji)

Jeżeli funkcje f i g mają granice właściwe w punkcie
, to

1. 
   

2. 
   

3. 
   

4. 
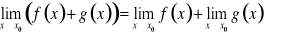
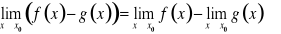
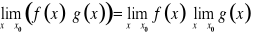
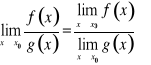
   , przy założeniu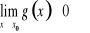
   

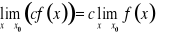
5. 
   , gdzie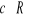
   

Uwaga. Powyższe twierdzenia o arytmetyce granic są prawdziwe także dla granic jednostronnych funkcji w punkcie x₀ oraz dla granic w -∞ lub ∞.

Tw. 3.17 (o granicy funkcji złożonej)

Jeżeli

,

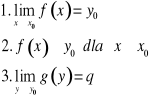
to

Fakt 3.18 (granice podstawowych wyrażeń nieoznaczonych)

ASYMPTOTY FUNKCJI

Def. 3.19 (asymptota pionowa lewostronna funkcji)

Prosta x = a jest asymptotą pionową prawostronną krzywej
, jeżeli

lub
.

Uwaga. Analogicznie definiuje się asymptotę pionową lewostronną. Prostą, która jest jednocześnie asymptotą pionową lewostronną i prawostronną funkcji nazywa się asymptotą pionową obustronną lub krótko asymptotą pionową. Funkcja elementarna może mieć asymptoty pionowe jedynie w skończonych krańcach swej dziedziny, które do niej nie należą.

Def. 3.20 (asymptota ukośna funkcji)

Prosta
jest asymptotą ukośną prawostronną (lub poziomą prawostronną, gdy a=0) krzywej
, wtedy i tylko wtedy, gdy

.

Uwaga. Analogicznie definiuje się asymptotę ukośną (poziomą) lewostronną funkcji (dla
). Prostą, która jest jednocześnie asymptotą ukośną (poziomą) lewostronną i prawostronną funkcji nazywamy asymptotą ukośną (poziomą) obustronną lub krótko asymptotą ukośną (poziomą).

Tw. 3.21 (warunek istnienia asymptoty ukośnej)

Prosta
jest asymptotą ukośną prawostronną krzywej
, wtedy i tylko wtedy, gdy

oraz
.

Uwaga. Prawdziwe jest także analogiczne twierdzenie o asymptotach ukośnych lewostronnych funkcji (dla
).

Fakt 3.22 (warunek istnienia asymptoty poziomej)

Prosta
jest asymptotą poziomą prawostronną krzywej
, wtedy i tylko wtedy, gdy

.

Uwaga. Analogicznie wygląda warunek istnienia asymptoty poziomej lewostronnej (dla
).

CIĄGŁOŚĆ FUNKCJI

Def. 3.23 (Heinego funkcji ciągłej w punkcie)

Niech będzie dana funkcja
,
oraz niech
. Funkcja f jest ciągła w punkcie x₀ wtedy i tylko wtedy, gdy dla każdego ciągu
o wyrazach ze zbioru
i zbieżnego do punktu
ciąg
jest zbieżny do punktu
, tj.

.

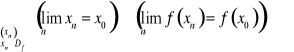
Uwaga Zauważmy, że w określeniu ciągłości funkcji f w punkcie
punkt
nie musi być punktem skupienia dziedziny
, jak w określeniu granicy funkcji. Konsekwencją tego jest ciągłość funkcji f w każdym punkcie izolowanym swej dziedziny. Granica funkcji f nie jest określona w żadnym takim punkcie. Jeżeli jednak funkcja f jest ciągła w punkcie
, który jest punktem
skupienia jej dziedziny
, to ma w tym punkcie granicę równą
,
i odwrotnie - jeżeli funkcja f ma w punkcie
granicę równą wartości funkcji w tym punkcie, to funkcja f jest ciągła w punkcie
. Zatem prawdziwe jest poniższe twierdzenie:

Tw. 3.24 (o funkcji ciągłej w punkcie będącym punktem skupienia dziedziny)

Funkcja f jest ciągła w punkcie x₀ będącym punktem skupienia dziedziny
wtedy i tylko wtedy, gdy

.

Def. 3.25 (Cauchy'ego funkcji ciągłej w punkcie)

Niech będzie dana funkcja
,
oraz niech
. Funkcja f jest ciągła w punkcie x₀ wtedy i tylko wtedy, gdy

.

Tw. 3.26 (o równoważności definicji ciągłości funkcji)

Definicje Heinego i Cauchy'ego ciągłości funkcji w punkcie są równoważne.

Def. 3.27 (funkcja lewostronnie ciągła w punkcie)

Niech funkcja f będzie określona przynajmniej na lewostronnym otoczeniu punktu x₀. Funkcja f jest lewostronnie ciągła w punkcie x₀ wtedy i tylko wtedy, gdy

.

Uwaga. Analogicznie definiuje się funkcję prawostronnie ciągłą w punkcie.

Tw. 3.28 (warunek konieczny i wystarczający ciągłości)

Funkcja f jest ciągła w punkcie x₀ wtedy i tylko wtedy, gdy jest lewostronnie i prawostronnie ciągła w tym punkcie, tj.

.

Def. 3.29 (funkcja ciągła na przedziale)

Funkcja f jest ciągła na przedziale, jeżeli jest ciągła w każdym punkcie tego przedziału.

NIECIĄGŁOŚĆ FUNKCJI

Def. 3.30 (nieciągłości pierwszego rodzaju)

Niech funkcja f będzie określona przynajmniej na otoczeniu punktu x₀. Funkcja f ma w punkcie x₀ nieciągłość pierwszego rodzaju, jeżeli istnieją granice skończone

oraz

lub
.

Uwaga. Mówimy, że funkcja f ma w punkcie x₀ nieciągłość pierwszego rodzaju typu „skok”, jeżeli spełnia warunek

.

Natomiast, jeżeli funkcja f spełnia warunek

,

to mówimy, że ma ona w punkcie x₀ nieciągłość pierwszego rodzaju typu „luka”.

Def. 3.31 (nieciągłość drugiego rodzaju)

Niech funkcja f będzie określona przynajmniej na otoczeniu punktu x₀. Funkcja f ma w punkcie x₀ nieciągłość drugiego rodzaju, jeżeli przynajmniej jedna z granic

nie istnieje lub jest niewłaściwa.

Uwaga. Nieciągłość funkcji można badać jedynie w punktach należących do jej dziedziny. Rozważa się także nieciągłości jednostronne funkcji.

TWIERDZENIA O FUNKCJACH CIĄGŁYCH

Tw. 3.32 (o ciągłości sumy, różnicy, iloczynu i ilorazu funkcji)

Jeżeli funkcje f i g są ciągłe w punkcie x₀, to:

1. funkcje f + g, f - g są ciągłe w punkcie x₀;

2. funkcja f⋅g jest ciągła w punkcie x₀;

3. funkcja
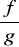
   jest ciągła w punkcie x₀, o ile g(x₀) ≠ 0.

Uwaga. Powyższe twierdzenie jest prawdziwe także dla funkcji ciągłych jednostronnie.

Tw. 3.33 (o ciągłości funkcji złożonej)

Jeżeli

1. funkcja f jest ciągła w punkcie x₀,

2. funkcja g jest ciągła w punkcie y₀ = f(x₀),

to funkcja złożona
jest ciągła w punkcie x₀.

Tw. 3.34 (o wprowadzeniu granicy do argumentu funkcji ciągłej)

Jeżeli istnieje granica właściwa
i funkcja h jest ciągła w punkcie
, to
.

Tw. 3.35 (o ciągłości funkcji odwrotnej)

Jeżeli funkcja
, gdzie A, B są dowolnymi przedziałami, jest ściśle monotoniczna i ciągła, to funkcja odwrotna
także jest ciągła.

Tw. 3.36 (o ciągłości funkcji elementarnych)

Funkcje elementarne są ciągłe w swoich dziedzinach.

Tw. 3.37 (o monotoniczności funkcji ciągłej i różnowartościowej)

Niech funkcja f będzie ciągła na przedziale [a,b]. Wówczas, funkcja f jest różnowartościowa na przedziale [a,b] wtedy i tylko wtedy, gdy jest malejąca albo rosnąca na tym przedziale.

49

---