Data	Wykonawcy	Temat ćwiczenia
29.10.1995	Grzegorz Stadryniak Andrzej Teuerle	Układy trójfazowe.

Schemat układu pomiarowego do badania obwodu trójfazowego z odbiornikiem połączonym w gwiazdę.

Schemat układu pomiarowego do badania obwodu trójfazowego z odbiornikiem połączonym w trójkąt.

Tabela pomiarowa do obwodu trójfazowego z odbiornikiem połączonym w gwiazdę.

Lp.	Stan pracy układu
		V	V	V	V	V	V	V	A	A	A	A	W	W	W
1.	Obciążenie symetryczne z przewodem zerowym	28	28	29	0	50	50	50	0.75	0.75	0.76	0.05	__	__	__
2.	Obciążenie symetryczne bez przewodu zerowego	28.1	28.1	29.1	0.3	50	50	50	0.76	0.76	0.80	0	33.7	35	68.7
3.	Przerwa w fazie B z przewodem zerowym	28	0	28	0	50	50	50	0.75	0	0.80	0.64	__	__	__
4.	Przerwa w fazie B bez przewodu zerowego	25	0	25	15.5	50	51	50	0.7	0	0.7	0	35	5	40
5.	Przerwa w fazie B i C z przewodem zerowym	27.1	0	0	0	50	29	27	0.7	0	0	0.65	__	__	__
6.	Obciążenie niesymetryczne z przewodem zerowym	27.5	27	29	0	50	50	50	1.09	0.93	0.8	0.23	__	__	__
7.	Obciążenie niesymetryczne bez przewodu zerowego	25	28	31	3	50	50	50	1	0.95	0.85	0	42.5	40	82.5

Tabela pomiarowa do obwodu trójfazowego z odbiornikiem połączonym w trójkąt

Lp	Stan pracy układu
		V	V	V	A	A	A	A	A	A	W	W	W
1.	Obciążenie symetryczne	48	50	50	2.03	2.05	2.1	1.1	1.7	1.2	87.5	92.3	179.8
2.	Obciążenie niesymetrycxzne	48	49	49	2.2	2.4	2.3	1.3	1.38	1.1	91	107.5	198.5
3.	Przerwa w obwodzie zasilania dla obciążenia symetrycznego	48	24	24	1.75	1.75	0	1.1	0.56	0.56	40	47.5	87.5
4.	Przerwa w jednej fazie odbiornika dla obciążenia symetrycznego	49	51	50	2.05	1.25	1.25	1.2	0	1.2	87.5	36	123.5

Uwagi i wnioski:

Moc czynna układu trójfazowego równa jest sumie poszczególnych mocy czynnych w każdej fazie. Moc czynną wyznaczliśmy metodą Arona - dwoma watomierzami. Można ją stosować w układach połączonych w trójkąt i połączonych w gwiazdę bez przewodu zerowego. Aby otrzymać moc całego układu dodaje się do siebie wskazania watomierzy. Moc można również wyliczyć w oparciu o zmierzone w ćwiczeniu wielkości. W układach połączonych w gwiazdę. Suma mocy czynnych w poszczególnych fazach równa jest całej mocy czynnej układu.

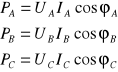
P = PA+PB+PC

Natomiast gdy układ trójfazowy połączony jest w trójkąt, moc czynną wyznaczamy sumując moce czynne poszczególnych faz.

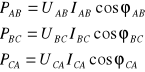
P = PAB+PBC+PCA

Ponieważ w badanym układzie obciążenie ma charakter rezystancyjny, kąty pomiędzy prądem fazowym a napięciem fazowym równe są zero, a cosinus jeden.

Występowanie w układzie trzech źródeł elektromotorycznych pozwala na różne połączenie tych sił - w gwiazdę lub trójkąt. Podobnie różne może być połączenie odbiorników. Chciałbym pokróce zająć się teraz każdym przypadkiem występującym w ćwiczeniach.

1. Układ trójfazowy symetryczny połączony w gwiazdę bez przewodu zerowego.

W układzie tym zarówno siły elektromotoryczne jak i odbiornik połączone są w gwiazdę. Występują w tym połączeniu dwa punkty zerowe. Odbiornik jest symetryczny.

Zespolone napięcia międzyfazowe równe są różnicy odpowiednich napięć fazowych :

UAB = UA-UB

UBC = UB-UC

UCA = UC-UA

Wykres wskazowy zamknięty jest w trójkącie. Dlatego napięcie pomiędzy punktami zerowymi wynosi zero. Moce czynne w poszczególnych fazach będą sobie równe, dlatego wystarczy wyliczyć moc w jednej fazie i pomnożyć przez trzy.

2. Układ symetryczny trójfazowy połączony w gwiazdę z przewodem zerowym.

Uzyskuje się to poprzez włączenie włącznika W0. Ponieważ w układzie bez przewodu zerowego napięcie pomiędzy punktami zerowymi wynosiło zero, połączenie ze sobą tych punktów nie wniosło żadnej zmiany w rozpływie prądów lub napięciach. Przez przewód nie płynie prąd. Wszystkie wartości pozostały takie same. Ponownie napięcia zamykają się w trójkącie co jest warunkiem, aby napięcie pomiędzy punktami zerowymi było równe zero. Również moce w układzie pozostają takie same.

3. Układ trójfazowy połączony w gwiazdę z przerwą w fazie B, bez przewodu zerowego.

Niesymetrię w układzie wprowadzimy poprzez wyłączenie fazy B. Spowoduje to, że z układu trójfazowego utworzy się układ jednofazowy, zawierający dwa źródła napięcia i dwa rezystory. Wyłączenie jednej fazy spowodowało spadek napięć fazowych oraz pojawienie się napięcia zerowego - - pomiędzy punktami zerowymi. Zmniejszyła się moc całego układu. Prąd IA równy jest co do wartości prądowi IC ale przeciwny w fazie.

4. Układ trójfazowy połączony w gwiazdę z przerwą w fazie B z przewodem zerowym.

Napięcie pomiędzy punktami zerowymi w poprzednim układzie spowodowało, że po połączeniu ich przewodem zerowym popłynął w nim prąd. Układ również zachowuje się jak układ jednofazowy, z dwoma źródłami napięcia i dwoma rezystorami. Jednak tym razem układ ma dwa oczka. W układzie moc po dołączeniu przewodu zerowego wzrosła.

5. Układ trójfazowy połączony w gwiazdę z przerwą w fazie B i C z przewodem zerowym.

Niesymetria układu pogłębiła się. Wyłączenie dwóch faz sprawiło, że układ stał się układem jednofazowym, zawierającym jedno tylko źródło napięcia i jeden rezystor. Prąd płynący w fazie A i płynący w przewodzie zerowym muszą być sobie równe. Ponownie znacznie spadła moc czynna w układzie.

6. Układ trójfazowy połączony w gwiazdę z obciążeniem niesymetrycznym, bez przewodu zerowego.

Innym sposobem wprowadzenia niesymetrii układu jest obciążenie rezystorami o różnej rezystancji. Pomiędzy punktami zerowymi pojawiło się napięcie. Napięcia międzyfazowe tworzą układ symetryczny jednak następuje przesunięcie punktu zerowego ze środka ciężkości trójkąta napięć zasilania o wektor U0.

7. Układ trójfazowy połączony w gwiazdę z obciążeniem niesymetrycznym z przewodem zerowym.

Jak można było przewidzieć na podstawie poprzednich rozważań po połączeniu ze sobą punktów zerowych układu w przewodzie popłynął prąd, będący na podstawie I prawa Kirchoffa sumą prądów fazowych.

Druga część ćwiczenia przeprowadzona była na odbiorniku połączonym w trójkąt. Nie ma już punktów zerowych układu, nie można ich połączyć przewodem zerowym. Zniknęły tym samym napięcia fazowe. Pojawiła się jednak nowa wielkość - prąd fazowy, płynący pomiędzy fazami.

1. Układ trójfazowy symetryczny połączony w trójkąt z obciążeniem symetrycznym.

Napięcia międzyfazowe tworzą regularny trójkąt, podobnie jak prądy przewodowe i fazowe. Moc wydzielana w tym układzie, w porównaniu z mocą w układzie połączonym w gwiazdę jest ponad dwukrotnie większa. Wartości poszczególnych prądów przewodowych wynoszą

IA = IAB - ICA

IB = IBC - IAB

IC = ICA - IBC

2. Układ trójfazowy połączony w trójkąt z obciążeniem niesymetrycznym

Do układu wprowadziliśmy niesymetrię poprzez nastawienie różnych wartości rezystancji w odbiorniku. Napięcia międzyfazowe nadal tworzą regularny trójkąt. Prądy też zamykają się w trójkącie zgodnie z I prawem Kirchoffa, jednak środek trójkąta nie pokrywa się z środkiem prądów fazowych. Moc układu bardzo wzrosła.

3. Układ trójfazowy połączony w trójkąt z przerwą w obwodzie zasilania i symetrycznym obciążeniem.

Wyłączyliśmy jedną fazę odbiornika, przez co układ trójfazowy zaczął zachowywać się jak układ jednofazowy z dwoma źródłami napięcia i włączonymi równolegle rezystorami. Na jednej gałęzi znajduje się jeden rezysor, na drugiej dwa rezystory. Z tego powodu prądy płynące przez rezystancje ZBC i ZAC są równe. Moc układu znacznie zmalała.

4. Układ trójfazowy połączony w trójkąt z przerwą w jednej fazie odbiornika i symetrycznym odbiornikiem.

Poprzez wyłączenie jednej fazy odbiornika otrzymaliśmy układ trójfazowy zachowujący się jak układ jednofazowy. Mamy trzy źródła napięcia i dwie oporności połączone w ten sposób, że tworzą dwa oczka. Napięcia fazowe tworzą trójkąt, natomiast prądy IAB i IC są sobie równe i w sumie dają prąd IA. Moc w układzie jest niewielka.

Na podstawie przeprowadzonych pomiarów możemy stwierdzić, że układy trójfazowe z odbiornikiem połaczonym w trójkąt są o wiele bardziej wydajne - można pobrać z nich większą moc

---