ANALIZA WSPÓŁZALEŻNOŚCI ZJAWISK

Przedmiotem analizy współzależności zjawisk jest badanie związków zachodzących pomiędzy różnymi cechami statystycznymi opisującymi zbiorowości statystyczne.

KORELACJA - wzajemne oddziaływanie lub współwystępowanie zjawisk lub cech tej samej zbiorowości.

REGRESJA - wpływ cechy traktowanej jako przyczyna (zmienna niezależna) na cechę traktowaną jako skutek (zmienna zależna) .

RODZAJE ZWIĄZKÓW:

FUNKCYJNY - gdy zmiana wartości jednej cechy (zmienna niezależna) powoduje ściśle określoną zmianę wartości drugiej cechy (zmienna zależna) np. pole koła jest funkcją jego promienia tzn. wszystkie koła o takim samym promieniu maja takie same pola.

STOCHASTYCZNY - gdy konkretnym wartościom jednej cechy (zmienna niezależna) odpowiadają różne wartości drugiej cechy (zmienna zależna) np. wśród rodzin o takim samym dochodzie na 1 osobę można zaobserwować różne wielkości spożycia artykułów nabiałowych.

KORELACYJNY - gdy określonym wartościom jednej cechy (zmienna niezależna) przyporządkowane są różne średnie warunkowe drugiej cechy (zmienna zależna).

Jest to szczególny przypadek związku stochastycznego.

Badanie związków ma sens jedynie wtedy, gdy pomiędzy cechami istnieje więź przyczynowo - skutkowa.

Może być ona jednostronna czyli

przyczyna®skutek

np. staż pracy a wydajność pracy;

lub dwustronna:

przyczyna®skutek i skutek®przyczyna

np. jednostkowy koszt produkcji i koszt produkcji.

FORMY OCENY ZWIĄZKU

1. TABELARYCZNA - szeregi, tablica korelacyjna

2. GRAFICZNA - diagram korelacyjny

3. PARAMETRYCZNA - charakterystyki liczbowe.

ZESTAWIENIE SZEREGÓW CECH ILOŚCIOWYCH:

Umożliwia określenie kierunku wzajemnych powiązań.

Przykład 1.

PRODUKT	NAKŁADY NA REKLAMĘ (W TYS)	WIELKOŚĆ SPRZEDAŻY	CENA JEDNOSTKOWA
A	1134	11254	35
B	1005	10896	38
C	2500	1985	26
D	674	702	54
E	334	475	63
F	980	1130	41

OCENA ZWIĄZKU:

Zmianom wartości jednej cechy towarzyszą zmiany wartości drugiej cechy, tzn. im wyższe nakłady na reklamę tym wyższe wielkości sprzedaży, natomiast im wyższa wielkość sprzedaży tym niższa cena jednostkowa produktu.

TABLICA KORELACYJNA - łączny rozkład zbiorowości według dwóch cech. Stosowana w przypadku licznej zbiorowości. Informuje nas o rodzaju związku oraz jego kierunku.

PRZYKŁAD 2

Zebrano informacje na temat grup kobiet, ich cech społecznych i demograficznych oraz wyniki badań psychologicznych.

liczba sztucznych poronień	Wiek w latach							razem
		17-22	22-27	27-32	32-37	37-42	42-47		47-52
1	1	1	5	3	4	6	3	23
2		1	1		1	2		5
3						1		1
4						1		1
razem	1	2	6	3	5	10	3	30

OCENA ZWIĄZKU:

ROZKŁADY BRZEGOWE - podają rozłożenie obserwacji oddzielnie dla każdej z obu cech.

ROZKŁADY WARUNKOWE - pokazują rozłożenie liczebności przy wartościach jednej cechy pod warunkiem, że druga przyjmie określoną wartość.

OBSERWACJA ROZKŁADÓW WARUNKOWYCH UMOŻLIWIA OCENĘ ZWIĄZKU POMIĘDZY ZMIENNYMI X I Y.

1. NIEZALEŻNOŚĆ STOCHASTYCZNA - zmieniającym się wartościom jednej cechy towarzyszą takie same rozkłady warunkowe drugiej cechy;

2. ZWIĄZEK STOCHASTYCZNY - zmieniającym się wartościom jednej cechy towarzyszą różne rozkłady warunkowe drugiej cechy;

3. ZWIĄZEK STATYSTYCZNY (KORELACYJNY) - ogranicza pole obserwacji do porównania średnich rozkładów warunkowych; zmieniającym się wartościom jednej cechy towarzyszą zmiany średnich warunkowych drugiej.

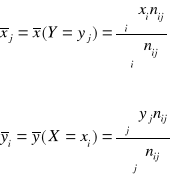
OBSERWACJA UŁOŻENIA DANYCH W TABLICY - położenie wzdłuż przekątnej;

DIAGRAM KORELACYJNY - umożliwia ocenę kształtu oraz kierunku badanego związku.

Y

X

Diagram (C) wykazuje, że pomiędzy cechami (x) i (y) nie zachodzi żadna korelacja.

Diagram (D) mówi, że pomiędzy cechami (x) i (y) zachodzi korelacja krzywoliniowa.

Diagramy (A) i (B) wskazują na istnienie korelacji liniowej. W przypadku diagramu (A) dodatniej a w diagramie (B) ujemnej.

FORMA PARAMETRYCZNA - polega na wyznaczeniu miary (współczynnika) odpowiedniej dla badanej cechy (ilościowej lub jakościowej).

Analiza współzależności zjawisk ekonomicznych polega na opisie:

*kształtu zależności (dzięki prezentacji graficznej badanych cech)

*kierunku zależności (kierunek zależności może być dodatni-wraz ze wzrostem wartości jednej cechy wzrasta wartość drugiej cechy lub ujemny-wraz ze wzrostem wartości jednej cechy maleją wartości drugiej cechy.)

*siły związku (badanie natężenia związku między cechami).

Prostymi metodami stwierdzania wzajemnych związków między cechami są:

a) gdy materiał jest w postaci szeregu:

*porównanie wartości liczbowych, które przyjmują

cechy w szeregu,

*konstrukcja diagramu korelacyjnego - rozkład

umieszczonych w prostokątnym układzie

współrzędnych punktów pozwala na wstępną

ocenę siły, kierunku i kształtu zależności;

b) gdy materiał jest w postaci tablicy korelacyjnej:

*ocena stopnia rozproszenia, bądź skupienia

liczebności warunkowych,

*konstrukcja empirycznych linii regresji- ich

graficzna prezentacja pozwala na wstępne

stwierdzenie siły, kierunku i kształtu zależności.

DO OCENY SIŁY ZWIĄZKU KORELACYJNEGO SŁUŻĄ M.IN.:

*współczynnik korelacji liniowej Pearsona

*współczynnik korelacji rang Spearmana

*współczynnik zbieżności Czuprowa

*stosunki korelacyjne

Korelację liniową mierzy się za pomocą współczynnika korelacji liniowej Pearsona, która ma postać:

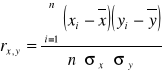
Właściwości współczynnika :

1. r_x,y = r_y,x korelacja pomiędzy (x) a (y) jest taka sama jak pomiędzy (y) a (x).

2. -1 ≤ r_x,y ≤ 1

Jeżeli r = ± 1 to mamy do czynienia z zależnością funkcyjną, matematyczną.

Jeżeli 0 < r < 1 to mamy do czynienia ze związkiem wprost proporcjonalnym.

Jeżeli - 1 < r < 0 to mamy do czynienia ze związkiem odwrotnie proporcjonalnym.

Jeżeli r jest nie większa niż 0,3 to mówimy, że korelacja jest niewyraźna, słaba;

Jeżeli r jest większa niż 0,3 a mniejsza niż 0.5 to mówimy, że korelacja jest średnia, umiarkowana.

Jeżeli r jest większa niż 0,5 to mówimy, że korelacja jest wyraźna, silna.

ZADANIE 3

W 20 losowo wybranych mieszkaniach zaobserwowano następujące relacje pomiędzy liczbą pokoi w mieszkaniu a liczbą zamieszkujących te pokoje osób.

Liczba pokoi (y)	7	1	5	4	2	3	6	5	4	3	2	2	1	3	5	4	5	3	4	1
Liczba osób (x)	6	1	6	4	2	2	5	4	3	3	3	1	3	4	4	4	5	4	5	1

1. Zbadać czy pomiędzy wymienionymi cechami zachodzi liniowy związek korelacyjny.

2. Oszacować wielkość mieszkania (liczbę pokoi) dla rodziny liczącej 4 osoby.

Z wykresu korelacyjnego wynika, że mamy do czynienia z istotnym, liniowym, dodatnim związkiem korelacyjnym. Oznacza to, że wraz ze wzrostem liczby osób w rodzinie rośnie ilość zajmowanych przez tę rodzinę pokoi (z układu punktów wynika, że współczynnik korelacji musi mieć znak dodatni (+), a wartość współczynnika musi być powyżej 0,6.

Ponieważ korelacja jest widoczna można przystąpić do oszacowania wielkości mieszkania dla 4 osobowej rodziny (szacujemy „y”).

Korzystamy w tym celu z linii regresji szacującej na podstawie której oszacujemy średnią wielkość (y) na podstawie (x = 4).

x	y	x -x	y -y	(x -x)⋅(y -y)	(x -x)^2	(y -y)^2
6	7	2,50	3,50	8,75	6,25	12,25
1	1	-2,50	-2,50	6,25	6,25	6,25
6	5	2,50	1,50	3,75	6,25	2,25
4	4	0,50	0,50	0,25	0,25	0,25
2	2	-1,50	-1,50	2,25	2,25	2,25
2	3	-1,50	-0,50	0,75	2,25	0,25
5	6	1,50	2,50	3,75	2,25	6,25
4	5	0,50	1,50	0,75	0,25	2,25
3	4	-0,50	0,50	-0,25	0,25	0,25
3	3	-0,50	-0,50	0,25	0,25	0,25
3	2	-0,50	-1,50	0,75	0,25	2,25
1	2	-2,50	-1,50	3,75	6,25	2,25
3	1	-0,50	-2,50	1,25	0,25	6,25
4	3	0,50	-0,50	-0,25	0,25	0,25
4	5	0,50	1,50	0,75	0,25	2,25
4	4	0,50	0,50	0,25	0,25	0,25
5	5	1,50	1,50	2,25	2,25	2,25
4	3	0,50	-0,50	-0,25	0,25	0,25
5	4	1,50	0,50	0,75	2,25	0,25
1	1	-2,50	-2,50	6,25	6,25	6,25
70	70	x	x	42,00	45,00	55,00

Średnia x x = 70 / 20 = 3,5

Średnia y y = 70 / 20 = 3,5

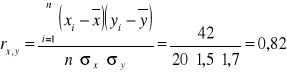
Obliczony współczynnik korelacji potwierdza istotną, liniową, dodatnia (wprost proporcjonalną) korelację pomiędzy wielkością rodziny i wielkością mieszkania. Logiczny związek pomiędzy tymi dwoma cechami oraz wysoki współczynnik korelacji sprawiają, że można przejść do oszacowania wielkości mieszkania dla 4 osobowej rodziny:

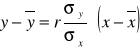
błąd oszacowania:

Wielkość mieszkania oszacowana przedziałowo z błędem (±1,02) pokoi wynosi (3,9 - 1,02 ; 3,9 + 1,02) czyli (3 ; 5)

Zadanie

Wyznaczyć linie regresji dla (x) i narysować wspólny wykres.

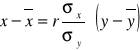
18

Korelacja krzywolinowa

r = 0

r < 0

r > 0

D

C

B

A

Błąd oszacowania

± Sy

pokoje

osoby

1

2

3

4

5

6

7

1

2

3

4

5

6

Współczynnik korelacji podajemy z dokładnością do 2 miejsc po przecinku

---