Tomasz Żmudziński

Wydział ETI.

Automatyka i Robotyka.

Studia inżynierskie.

Ćwiczenie nr 25.

Wyznaczanie rozmiarów szczelin i przeszkód za pomocą światła laserowego.

Dane stanowiska doświadczalnego:

Długość fali lasera λ=632.8 nm.

Odległość szczeliny od ekranu L [cm].

Odległość pomiędzy kolejnymi maksimami odpowiedniego rzędu X_n [cm].

Średnica krążka Airy'ego d [cm].

Wyniki pomiarów:

1.Szczelina z żyletki, badanie:

a) pierwsze: b) drugie:

L =96,0 L =97,9

X₁= 3,9 X₁= 1,4

X₂= 6,7 X₂= 2,4

X₃= 9,8 X₃= 3,8

2.Szczelina nastawna, badanie:

pierwsze: b) drugie: c) trzecie:

L =100,3 L= 91,1 L = 88,0

X₁= 1,1 X₁= 1,0 X₁= 1,0

X₃= 2,7 X₃= 2,4 X₃= 2,3

X₅= 4,0 X₅= 3,8 X₅= 3,7

3.Siatka dyfrakcyjna, badanie:

pierwsze: b) drugie: c) trzecie:

L = 89,9 L = 48,8 L= 23,5

X₁=23,0 X₁=12,6 X₁= 6,2

X₂=25,4 X₂=14,0

4.Otwór jawny, badanie:

pierwsze: b) drugie: c) trzecie:

L=99,8 L=83,2 L=71,0

d= 0,6 d= 0,5 d = 0,4

5.Otwór w postaci przesłony, badanie:

pierwsze: b) drugie: c) trzecie:

L=88,4 L=70,0 L=50,9

d=1,2 d=1,0 d=0,6

6.Drucik nr 6, badanie:

a) pierwsze: b) drugie: c) trzecie:

L= 101,9 L=83,2 L=73,0

X₁=2,0 X₁=5,1 X₁=4,4

X₂=10,0 X₃=11,8 X₃=10,4

X₄=18,2 X₅=18,5 X₅=16,6

7.Drucik nr 5, badanie:

pierwsze: b) drugie: c) trzecie:

L=98,6 L=85,5 L=74,5

X₁=3,8 X₁=3,2 X₁=2,9

X₃=8,8 X₃=7,6 X₃=6,6

X₅=14,2 X₆=14,1 X₆=12,4

Opis ćwiczenia nr 25.

Wyznaczanie rozmiarów szczelin i przeszkód za pomocą światła laserowego.

Do wyznaczenia rozmiarów szczelin i przeszkód wykorzystam zjawisko dyfrakcji i interferencji światła. Warunkiem uzyskania wyraźnego i niezakłóconego obrazu jest koherencja światła. Oznacza to zgodność między fazami w różnych punktach wiązki światła lub w różnych wiązkach światła. Rozróżniamy spójność światła czasową i przestrzenną. Spójność czasowa jest to zgodność fazowa pomiędzy wiązkami światła wychodzącego z jednego punktu źródła światła rozciągłego po przebyciu przez nie pewnej drogi optycznej, zwaną długością spójności .Wyrażamy ją wzorem:

gdzie c - prędkość światła,

v - szerokość widmowa.

Spójność przestrzenna światła to zgodność fazowa między wiązkami światła pochodzącymi z dwóch różnych punktów źródła rozciągłego. Wyrażamy ją wzorem:

τ

gdzie L_c - długość spójności

c - prędkość światła.

Wszystkie przeszkody znajdujące się na drodze fal świetlnych powodują zakłócenia kształtu powierzchni falowych, co prowadzi do zjawiska dyfrakcji światła. Twierdzenie Babineta pozwala traktować jednakowo przeszkody i otwory o tych samych rozmiarach. Oznacza to, że obraz interferencyjno-dyfrakcyjny przeszkody o średnicy D jest taki sam jak otworu o takiej samej średnicy.

W doświadczeniu wykorzystam laser He-Ne (helowo-neonowy), który poprzez wykorzystanie zjawiska wymuszonej emisji, zapewni wysoki stopień spójności i monochromatyczności światła.

Sposób ustawienia lasera, obiektów badanych i ekranu przedstawia poniższy schemat:

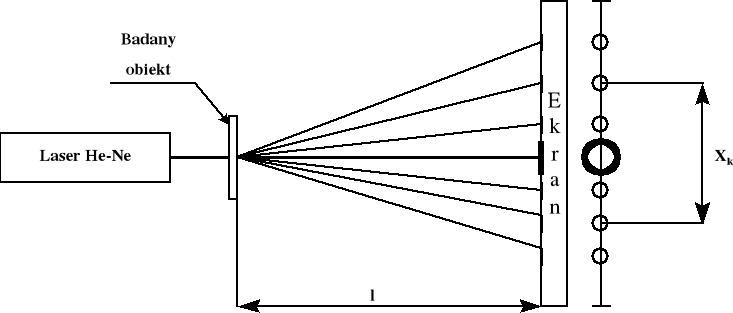
gdzie l - odległość pomiędzy obiektem badanym a ekranem,

X_k - odległość pomiędzy maksimami (jasnościami) odpowiedniego rzędu.

Wyznaczając:

1) Stałą siatki dyfrakcyjnej posłużę się wzorem:

gdzie: k - rząd maksimum,

λ - długość fali,

l - odległość ekranu od siatki,

x_k- odległość między środkami maksimów k- tego rzędu,

a - szukana stała siatki.

1) Wykonując obliczenia według wzorów otrzymujemy:

dla k=1 oraz l=89.9 cm otrzymaliśmy x=11,6 +11,4=23 cm, więc:

a={2*1*0,899*632,8*10^-9*[1-(0,23)²/4*(0,899)²]^1/2}/0,23=

= 1137,7744* 1,0080*10^-9/0,23=9,81*10^-3 [m]

|Da|/a=|Dl|/l+|Dx|/x=|1*10^-3|/0,899 +|2*10^-3|/0,23=9,81*10^-3

Tabela wyników (stała siatki):

l [m]	k	x [m]	a[m*10^-6]	|Da|/a [*10^-3]	Da [m*10^-8]
0,899	1	0,230	4,959	9,81	4,865
0,488	1	0,126	4,944	17,9	8,850
0,488	2	0,254	5,033	9,91	4,994
0,235	1	0,062	4,982	36,5	18,18
0,235	2	0,140	5,030	18,5	9,31

Średnio otrzymujemy więc: a=( 4,990 K 0,182)*10^-6 [m]

Szerokość szczelin i drutów posłużę się wzorem:

gdzie: k - rząd widma,

λ - długość fali,

l - odległość obiektu badanego od ekranu,

x_k- odległość między środkami maksimów k- tego rzędu,

d - szukana szerokość szczeliny lub przeszkody.

obliczając dla uzyskanych danych :

a) szczelina przestawna :

-dla l=100,3 cm , k=1, x=0,5+0,6=1.1 cm otrzymujemy według wzoru:

d=[(2*1+1)*1,003*632,8*10^-9]/0,011=1,904*10^-6/0,011= 1,731*10^-4 [m]

|Dd|/d=|Dl|/l+|Dx|/x=|0,001|/1,003+|0,002|/0,011=0,183

Tabela wyników dla szczeliny nastawnej:

l [m]	k	x [m]	d[m*10^-4]	|Dd|/d	Dd [m*10^-4]
1,003	1	0,011	1,731	0,183	0,316
1,003	3	0,027	1,777	0,081	0,144
1,003	5	0,040	1,745	0,051	0,089
0,911	1	0,010	1,729	0,201	0,348
0,911	3	0,024	1,681	0,168	0,282
0,911	5	0,038	1,669	0,054	0,090
0,880	1	0,010	1,671	0,201	0,336
0,880	3	0,023	1,695	0,088	0,149
0,880	5	0,037	1,656	0,055	0,091

Średnio otrzymujemy: d=(1,701 K 0,348) * 10^-4 m

Tabela wyników dla żyletek (dwa pomiary):

Szczelina	l [m]	k	x [m]	d[m*10^-4]	|Dd|/d	Dd [m*10^-4]
1	0,960	1	0,039	4,673	0,0523	0,245
1	0,960	2	0,067	4,533	0,0309	0,140
1	0,960	3	0,098	4,339	0,0214	0,093
2	0,979	1	0,014	13,28	0,1439	1,911
2	0,979	2	0,024	12,91	0,0844	1,090
2	0,979	3	0,038	11,41	0,0537	0,612

Średnio otrzymujemy:

- pomiar 1 : d=(4,515 K 0,245) * 10^-5 m

- pomiar 2 : d=(12,53 K 1,91) * 10^-4 m

Tabela wyników dla drutów (dwa druty):

Liczba porządkowa	Nr drutu	l [m]	k	x [m]	d[m*10^-5]	|Dd|/d	Dd [m*10^-5]
1	6	1,019	1	0,020	3,224	0,101	0,326
2	6	1,019	2	0,100	3,224	0,021	0,068
3	6	1,019	4	0,182	3,137	0,012	0,037
4	6	0,832	1	0,051	3,097	0,040	0,125
5	6	0,832	3	0,118	3,123	0,018	0,057
6	6	0,832	5	0,185	3,130	0,012	0,038
7	6	0,730	1	0,044	3,150	0,047	0,147
8	6	0,730	3	0,104	3,109	0,021	0,064
9	6	0,730	5	0,166	3,061	0,013	0,041
10	5	0,986	1	0,038	4,926	0,054	0,264
11	5	0,986	3	0,088	4,963	0,024	0,118
12	5	0,986	5	0,142	4,833	0,015	0,073
13	5	0,855	1	0,032	0,073	0,064	0,323
14	5	0,855	3	0,076	4,983	0,027	0,137
15	5	0,855	6	0,141	4,988	0,015	0,077
16	5	0,745	1	0,029	4,877	0,070	0,343
17	5	0,745	3	0,066	5,000	0,032	0,158
18	5	0,745	6	0,124	4,942	0,017	0,086

Średnio otrzymujemy:

- drut 6 : d=(3,140 K 0,326) * 10^-5 m

- drut 5 : d=(4,954 K 0,326) * 10^-5 m

Średnice otworów i przeszkód owalnych posłużę się wzorem:

gdzie: λ - długość fali,

l - odległość obiektu badanego od ekranu,

D - Średnica krążka Airy'ego,

d - szukana średnica otworu.

-dla l=0,884 m , d=0,012 m otrzymujemy według wzoru:

d=1,22*0,884*(632,8*10^-9 /0,012)=1,078*5,273*10^-5 =5,687*10^-4 [m]

|Dd|/d=|Dl|/l+|DD|/D=|0,001|/0,884+|0,002|/0,012=0,168

Tabela wyników dla dziury i przeszkody:

	l [m]	D [m]	d[m*10^-5]	|Dd|/d	Dd [m*10^-5]
przeszkoda	0,884	0,012	5,687	0,168	0,954
przeszkoda	0,700	0,010	5,404	0,201	1,086
przeszkoda	0,509	0,006	6,549	0,335	2,195
dziura	0,998	0,006	12,84	0,334	4,293
dziura	0,832	0,005	12,85	0,401	5,154
dziura	0,710	0,004	13,70	0,501	6,864

Średnio otrzymujemy:

- przeszkoda : d=(5,880 K 2,195) * 10^-5 m

- dziura : d=(13,13 K 6,864) * 10^-5 m

Błędy pomiarowe odległości wynoszą:

- 1 mm dla odległości l,D

- 2 mm dla odległości x.

Bibliografia:

-R.Resnick „Fizyka” PWN Warszawa 1996

-Praca zbiorowa:” I laboratorium z fizyki” .Wyd.PG. Gdańsk 1997

---