Współczynnik korelacji liniowej oraz funkcja regresji liniowej dwóch zmiennych

1. Poniższe dane ukazują liczbę studentów oraz liczbę pracowników naukowo - dydaktycznych w Akademii Ekonomicznej w latach od 1990 - 1999

lata	i	liczba studentów xi	liczba pracowników yi
1990	1	4780	417
1991	2	4975	463
1992	3	7732	433
1993	4	9701	487
1994	5	12154	506
1995	6	14300	518
1996	7	15766	554
1997	8	17516	563
1998	9	18355	575
1999	10	18633	594
xxx	suma	123912	5110

Na podstawie powyższych informacji ustalić siłę i kierunek współzależności obu zmiennych.




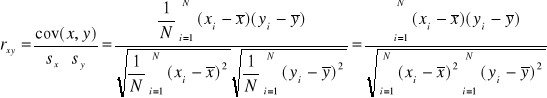
i	liczba studentów xi	liczba pracowników yi			( )* ( )
1	4780,00	417,00	-7611,20	-94,00	715452,80	57930365,44	8836,00
2	4975,00	463,00	-7416,20	-48,00	355977,60	55000022,44	2304,00
3	7732,00	433,00	-4659,20	-78,00	363417,60	21708144,64	6084,00
4	9701,00	487,00	-2690,20	-24,00	64564,80	7237176,04	576,00
5	12154,00	506,00	-237,20	-5,00	1186,00	56263,84	25,00
6	14300,00	518,00	1908,80	7,00	13361,60	3643517,44	49,00
7	15766,00	554,00	3374,80	43,00	145116,40	11389275,04	1849,00
8	17516,00	563,00	5124,80	52,00	266489,60	26263575,04	2704,00
9	18355,00	575,00	5963,80	64,00	381683,20	35566910,44	4096,00
10	18633,00	594,00	6241,80	83,00	518069,40	38960067,24	6889,00
sumy	123912,00	5110,00	0,00	0,00	2825319,00	257755317,60	33412,00








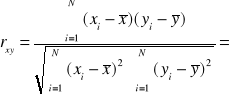
Współczynnik determinacji:




Współczynnik indeterminacji:




Zarówno współczynnik determinacji jak i indeterminacji po przemnożeniu przez 100 można wyrazić w procentach.

Wówczas współczynnik determinacji informuje nas, w jakim procencie zmienność jednej zmiennej (X lub Y) można wyjaśnić zmiennością drugiej zmiennej (Y lub X).

Obliczając współczynnik indeterminacji dowiemy się, w jakim procencie zmienność jednej ze zmiennych (X lub Y) nie zależy od zmienności drugiej (Y lub X), lecz od innych czynników losowych.

Aproksymacja funkcji liniowej postaci y = ax + b




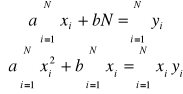
Parametry a i b:













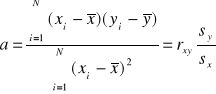
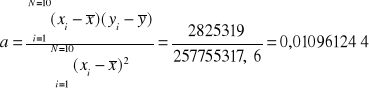
funkcja regresji:




i	liczba studentów xi	liczba pracowników yi
1	4780	417	427,5718	-10,5718	111,7625
2	4975	463	429,7092	33,29078	1108,276
3	7732	433	459,9294	-26,9294	725,191
4	9701	487	481,5121	5,487939	30,11748
5	12154	506	508,4	-2,39999	5,759966
6	14300	518	531,9228	-13,9228	193,845
7	15766	554	547,992	6,007993	36,09598
8	17516	563	567,1742	-4,17418	17,42382
9	18355	575	576,3707	-1,37067	1,878732
10	18633	594	579,4179	14,58211	212,6378
suma	123912	5110			2442,988

Współczynnik determinacji




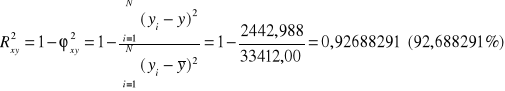
Współczynnik indeterminacji




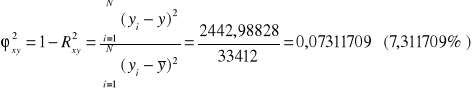
Wariancja resztowa




odchylenie standardowe składnika resztowego







Współczynnik korelacji dwuseryjnej

Jeżeli jedna ze zmiennych jest zmienną ciągłą (np. zmienna Y) a druga zmienna jestzmienną zero - jedynkową (np. zmienna X), to do określenia siły współzależności pomiędzy zmiennymi można wykorzystać tzw. współczynnik korelacji dwuseryjnej

(r_d.xy) postaci:


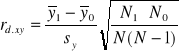
, (7)

gdzie:


- średnia arytmetyczna realizacji zmiennej Y, skojarzonych z realizacjami zmiennej X o wartości 0,


- średnia arytmetyczna realizacji zmiennej Y, skojarzonych z realizacjami zmiennej X o wartości 1,


- odchylenie standardowe zmiennej Y,

N₀ - liczebność podzbioru zer,

N₁ - liczebność podzbioru jedynek,

N = N₀ + N₁.

Przykład 2

W celu zbadania wpływu uczestnictwa na wykładzie na wyniki otrzymane ze sprawdzianu ze statystyki, poddano badaniu grupę 10 studentów. Pierwszą z cech oceniano na skali dwupunktowej w następujący sposób:




natomiast druga z cech była oceniana na skali punktowej od 0 do 25 punktów

Otrzymano następujące wyniki:

student i	obecność xi	liczba punktów yi
1	1	15,5
2	0	12
3	0	13
4	1	20
5	0	8
6	0	10
7	1	20,5
8	0	14
9	1	19
10	1	18

Źródło: badania własne

Czy istnieje współzależność pomiędzy wynikami ze sprawdzianu a obecnością podczas wykładu?

Średnia ilość punktów wyniosła:


Obliczania pomocnicze

student i	obecność xi	liczba punktów yi
1	1	15,5	0,5	0,25
2	0	12	-3	9
3	0	13	-2	4
4	1	20	5	25
5	0	8	-7	49
6	0	10	-5	25
7	1	20,5	5,5	30,25
8	0	14	-1	1
9	1	19	4	16
10	1	18	3	9
suma	5	150		168,5

Źródło: Obliczenia własne

Wariancja i odchylenie standardowe zmiennej Y wyniosły:


;


.

Wartości
i
, N, N₀ i N₁, obliczamy następująco:


,


.

N₀ = N₁ = 5 => N = 10.

Zatem współczynnik korelacji dwuseryjnej wyniesie:


.

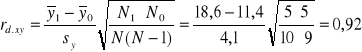
Uzyskany wynik świadczy o bardzo dużym związku pomiędzy obecnością podczas wykładu a ilością uzyskanych punktów podczas sprawdzianów kontrolnych.

Współczynnik skojarzenia

Zmienne X i Y, to zmienne zero - jedynkowe.

Rozkład wartości zmiennych oraz ich liczebności przedstawia poniższa tablica.

		Y		Σ
					0	1
	X	0	f(0;0)	f(0;1)	f(0;0) + f(0;1)
		1	f(1;0)	f(1;1)	f(1;0) + f(1;1)
Σ		f(0;0) + f(1;0)	f(0;1) + f(1;1)	N

W ostatniej kolumnie i w ostatnim wierszu tablicy zapisuje się liczebności brzegowe zmiennej X i zmiennej Y.

Współczynnik skojarzenia (Q_xy) oblicza się stosując wzór:


(8)

Przykład 3

60 studentów regularnie przygotowywało się do zajęć ze Statystyki, a 40 sporadycznie. w grupie pierwszej egzaminy poprawkowe zdarzyły się 10 razy w ciągu studiów, a w drugiej aż 30. Czy istnieje związek pomiędzy solidnością pracy i koniecznością poprawkowych egzaminów? Uzasadnić odpowiedź posługując się odpowiednim miernikiem

Przyjmijmy następujące oznaczenia:

X = 0, jeżeli student zdał egzamin w pierwszym terminie

X = 1, jeżeli student miał egzamin poprawkowy

Y = 0, jeżeli student uczył się regularnie

Y = 1, jeżeli student uczył się sporadycznie

Tablica korelacji ma postać:

		Y		Σ
					0	1
	X	0	50	10	60
		1	10	30	40
Σ		60	40	100




Otrzymany wynik świadczy o wysokiej dodatniej współzależności pomiędzy solidnością pracy a terminem zdania egzaminu.

Współczynnik korelacji rang Spearmana

Współczynnik korelacji rang stosuje się wówczas, gdy wartości cech mierzalnych opisanych przez odpowiednie zmienne (ciągłe lub skokowe) lub warianty cechy niemierzalnej, zostały zastąpione rangami, czyli kolejnymi liczbami.


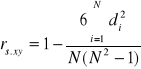
(8)

gdzie


oznacza różnicę pomiędzy rangami zmiennej X i Y,

N - ilość par obserwacji zmiennej X i Y.

Podobnie jak klasyczny współczynnik korelacji liniowej, współczynnik korelacji rang przyjmuje wartości z przedziału [-1; 1]. Jeżeli r_s.xy= -1, to oznacza to pełną przeciwstawność uporządkowań, gdy r_s.xy= 1, uporządkowania są w pełni zgodne, natomiast, gdy r_s.xy= o, to mówimy o całkowitym braku uporządkowań.

Współzależność wielu zmiennych, korelacja cząstkowa i wieloraka.

Funkcja regresji wielu zmiennych

Mając następujące dane dotyczące produkcji dwu różnych wyrobów w sztukach oraz zużycie energii na tę produkcję w sześciu kolejnych okresach:

okres	produkcja L x1i	produkcja K x2i	zużycie energii w kWh yi
1	2	3	12
2	4	2	14
3	3	1	11
4	5	3	15
5	2	2	14
6	2	1	6

1. oszacować za pomocą metody najmniejszych kwadratów parametry funkcji regresji typu y = a_o + a₁x₁ + a₂x₂, gdzie Y oznacza zużycie energii elektrycznej, X₁ - produkcję wyrobu L, X₂ produkcje wyrobu K,

2. zbadać dobroć dopasowania funkcji regresji,

3. obliczyć współczynniki korelacji cząstkowej.

Rozwiązanie







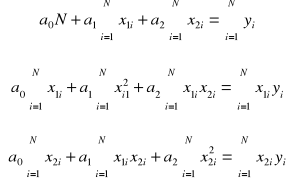
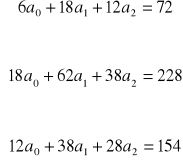
a₀ = 5; a₁ = 1; a₂ = 2

Równanie regresji liniowej będzie miało postać:




Wariancja resztowa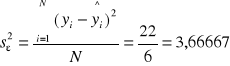


Odchylenie standardowe składnika resztowego


Współczynnik indeterminacji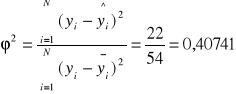


Współczynnik determinacji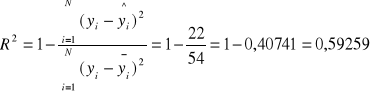


Współczynnik korelacji wielorakiej





okres	produkcja L x1i	produkcja K x2i	zużycie energii w kWh yi
1	2	3	12	4	6	9	24	36	0	13	1
2	4	2	14	16	8	4	56	28	4	13	1
3	3	1	11	9	3	1	33	11	1	10	1
4	5	3	15	25	15	9	75	45	9	16	1
5	2	2	14	4	4	4	28	28	4	11	9
6	2	1	6	4	2	1	12	6	36	9	9
suma	18	12	72	62	38	28	228	154	54		22
średnie	3	2	12

okres
1	0	0	-1	1	1	0
2	2	0	0	1	0	4
3	0	1	0	0	1	1
4	6	3	2	4	1	9
5	-2	0	0	1	0	4
6	6	6	1	1	1	36
suma	12	10	2	8	4	54

Przyjmiemy następujące założenia: Y - 0; X₁ - 1; X₂ - 2. Wówczas współczynniki korelacji r₀₁­ = 0,57735; r₀₂ = 0,68041 i r₁₂ = 0,35355




Macierz współczynników korelacji:


Wyznacznik macierzy |R| = 0,35648

Współczynniki korelacji cząstkowej.


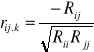
, gdzie R_ij, R_ii, R_jj są dopełnieniami algebraicznymi macierzy R.

R₀₀ = 0,875; R₁₁ = 0,53704;R₂₂ = 0,66667;

R₀₁ = -0,33679; R₀₂ = -0,47629; R₁₂ = 0,03928








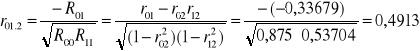
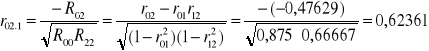
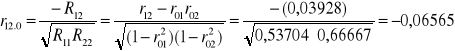
Korelacja wieloraka







---