1

Ile wynosi standardowa zmiana entalpii reakcji , której stała równowagi rośnie dwukrotnie, gdy temperatura zmienia się od 315 K do 347 K? Wynik podać w kJ/mol.

Odpowiedź: 19.685

Wzór: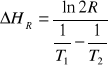

2

Mol jednoatomowego gazu doskonałego zamkniętego w cylindrze z ruchomym tłokiem podgrzano od 407 K do 594 K. Oblicz zmianę entalpii tego procesu. Wynik podać w J.

Odpowiedź: 3886.795

Wzór:

3

W pewnym procesie izochorycznym zależność energii swobodnej układu od temperatury wyraża równanie F = 63.7 + 71.8T [J]. Ile wynosi zmiana entropii układu w tym procesie? Wynik podaj w J•K-1.

Odpowiedź: -71.8

Wzór:
=> wystarczy przepisać z danych ale uwaga na znak!!

4

Substancje A i B tworzą roztwory doskonałe. W 30oC prężności par nasyconych tych związków wynoszą odpowiednio 293.1 kPa i 50 kPa. Roztwór o składzie molowym xA = 0.46 i temperaturze 30oC zamknięto w cylindrze z ruchomym tłokiem obciążonym ciśnieniem p. Obliczyć, jaki będzie stosunek liczby moli fazy ciekłej do gazowej, gdy ciśnienie będzie wynosiło 0.9 ciśnienia, w którym układ ten zaczyna wrzeć. (wynik podaj z dokładnością do 0.01)

Odpowiedź: 5

1. p wrzenia=xA*pA0 + (1-xA)*pB0

2. p=0,9 * p wrzenia

3. p=xA'*pA0+(1-xA')*pB0 => xA' = p-pB0/pA0-pB0

4. y=(xA'*pA0)/p

5. n cieczy/n pary = (y-xA)/(xA-xA')

5

Obliczyć średnie ciepło parowania złota, jeśli wiadomo, że temperatura wrzenia pod ciśnieniem 74533 Pa wynosi 3153 K a 2664 K pod ciśnieniem 6557 Pa. Wynik podać w J/mol.

Odpowiedź: 347130.109

Wzór: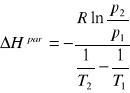

6

Standardowa entalpia tworzenia gazowego toluenu wynosi 50.00 kJ/mol w temperaturze T=298K. Znając standardowe entalpie tworzenia: Htw,CO2(g)(298K)=-393.77 kJ/mol i Htw,H2O(c)(298K)=-285,9 kJ/mol. obliczyć standardową entalpię spalania tego związku. Podać wynik w kJ/mol.

Piszemy reakcje i uzupełniamy współczynniki:

(delta H) = -(delta)
+7(delta)
+4(delta)

Odpowiedź: -3949.99

7

Molowa pojemność cieplna pary wodnej pod stałym ciśnieniem określa równanie: Cp=28.83+13,74*10do-3T -1.435*10do-6T2 J/molK. Ile ciepła wydzieli się podczas ochładzania 155g pary wodnej od temp 390°C do100°C pod ciśnieniem 1 atm. M h2o to 18g/mol. Podać wynik w kJ

Odpowiedź: -89.56

Cp=28,83+13.74*10^-3T-1.435*10^-6T^2
n=m/M=155/18=8,61
T1=390°C=663 K
T2=100°C=373 K

deltaH= n* całka od T1 do T2 z (28,83+13.74*10^-3T-1.435*10^-6T^2)
deltaH=8,61 [28,83*(373-663)+13.74*10^-3*(373^2-663^2)/2-1.435*10^-6*(373^3-663^3)/3]

8

Gdy 7.3 mole gazu spełniającego równanie stanu gazu doskonałego, zajmującego w temperaturze 340.5K 59dm3 poddano izotermicznemu rozprężaniu, jego entropia wzrosła o 6.6 J*K-1. Oblicz F tego procesu, wynik podaj w J.

Odpowiedź: -2247.3

Wzór:

9

Obliczyć entropię molową dwuatomowego gazu doskonałego w temperaturze 273 K, pod ciśnieniem 852630 Pa wiedząc, że molowa entropia standardowa Sº tego gazu w temperaturze 298 K wynosi 197.4 J·K-1.

Odpowiedź: 177.87

Wzór: S=S° + 5/2R ln(T/T0) - Rln p/p0

10

Gaz doskonały (liczba moli gazu wynosi 2.11) o temperaturze 308K rozprężano izotermicznie w sposób odwracalny. Jaką pracę wykonał gaz, jeśli jego ciśnienie zmalało 1.4-krotnie? Wynik podać w J.

Odpowiedź: -1817.99

Wzór: W = -nRT ln1.4

11

9.4 moli dwuatomowego gazu doskonałego znajdujących się w warunkach standardowych rozpręża się adiabatycznie przesuwając tłok obciążony ciśnieniem 53665 Pa do wyrównania ciśnień po obu stronach tłoka. Obliczyć zmianę entropii tego procesu. Wynik podać w J•K-1.

Odpowiedź: 10.19

pzew=p2

Wzór: T2 = {[pT1/p1] + [5/2T1]} / [7/2]

S = n7/2RlnT2/T1 - nRln p2/p1

12

W stalowym cylindrze o objętości 6 dm3 zamknięto 0.1 mola związku A3(g) i ogrzano do temperatury 691 K. Wiedząc, że w reakcji A3(g) = 3A(g) rozpadło się 36 % trimerów, obliczyć stałą równowagi reakcji Kp w tej temperaturze. Gazy A3 i A traktować jak gaz doskonały.

Odpowiedź: 1.8

Wzór:

A3 => 3A

początek 0,1<A3> ; 0<3A>

reakcja -ξ <A3> ; 3ξ<3A>

równowaga 0,1-ξ <A3> ; 3ξ<3A> n(tot)=0,1+2ξ=0,172

ξ=0,36*0,1=0,036

p(tot)=n(tot)RT/V=164689,25

X(A3)=n(A3)/n(tot)=0,1-0,036/0,172=0,372

X(3A)= n(3A)/n(tot)=3*0,036/0,172=0,628

Kp={[X(3A)•p(tot)/p°]^3}/{X(A3)•p(tot)/p°}=1,758

13

Reakcja 2A+B=3C+D przebiega w fazie gazowej. Gdy zmieszano 1 mol A, 2 mole B i 1 mol D, po ustaleniu się równowagi w temp. 301 k i pod ciśnieniem 2 atm, mieszanina zawierała 0.9 mola C. Oblicz ułamek molowy B w stanie równowagi.

Odpowiedź: 0.4

Wzór:

2A + B = 3C + D

n pocz 1 2 (-) 1

n reaguje -2x -x 3x x

n rowno. 1-2x 2-x 3x 1-x

ul molowe (1-2x)/(4+x) (2-x)/(4+x) 3x/(4+x) (1-x)/(4+x)

n całkowite=(1-2x)+(2-x)+3x+(1-x)= 4+x

podają nam liczność C= 3x=0.9

x=0.3

Xb=(2-x)/(4+x) Przeważnie wchodzi wynik 0.4 :P

14

Opierając się na danych z poniższej tabeli, obliczyć wartość lnKp reakcji 2A(g) + B(g) = 2C(g) w temperaturze 374 K, zakładając niezależność i od temperatury.

Odpowiedź: 6.1

...........So..........delta [H]tw

A(g)... 188 ......... 62.08

B(g) ...205.6........ 0

C(g)... 240.5........33.85

Wzór:

delta S=2C-2*A-B

delta H=2*C-2*A

A= -deltaH + TdeltaS

A=RTlnKp

lnKp=A/(R*T)

Tylko trzeba uważać na jednostki, bo przeważnie S podawane jest w [J/molK] a deltaH w [kJ/mol]!!

15

4.1 moli metanu znajdujących się w warunkach standardowych (T1=273.15, p=1,01325*105Pa) rozpręża się adiabatycznie przesuwając tłok obciążony ciśnieniem 50027Pa do wyrównania ciśnień po obu stronach tłoka. Obliczyć zmianę entropii tego procesu. Metan spełnia równanie sztywnych kul (b=42.8*10-6m3*mol-1)

Odpowiedź: 5.6

Nie bierzemy wartości temp. z nawiasu!! (standardowa to 298K); Cv metanu =>3R; Cp=>4R; pzew=p2

Wzór: T2 = {[pT1/p1] + [3T1]} / [4]

S = n4RlnT2/T1 - nRlnp2/p1

16

Oblicz zmianę energii swobodnej w kwazistatycznym procesie izotermicznego sprężania 7 moli gazu doskonałego, od ciśnienia p1 do ciśnienia p2 w temperaturze T. Wynik podaj w J. 

T= const. i proces kwazistatyczny 

(delta)G=-T(delta)S=-T(-nR [całka od p1 do p2]dp/p)=-T(-nRln[p2/p1])=nRT ln[p2/p1] 

17

1.15 moli 1-atomowego gazu doskonałego o początkowej temperaturze 327K podlega przemianie, której towarzyszy zmiana entalpii równa -1630J. Obliczyć końcową temperaturę gazu.

Odpowiedź: 258.81

Wzór: T2=[2H+n5RT1]/[n5R]

18

4.12 moli tlenu pod początkowym ciśnieniem 52 kPa i o początkowej temperaturze 269 K rozprężało się adiabatycznie, przesuwając tłok obciążony ciśnieniem 25.1 kPa aż do wyrównania się ciśnień po obu stronach tłoka. Obliczyć pracę wykonaną przez układ. Wynik podać w dżulach, ciepło właściwe oszacować na podstawie geometrii cząsteczki tlenu. Tlen opisać równaniem stanu gazu doskonałego.

Odpowiedź: -3404.82

Wzór: T2 = {[pT1/p1] + [5/2T1]} / [7/2]

W=n5/2R(T2-T1)

---