Omówić pojęcie: układ, otoczenie, parametry stanu układu:

Układ - przez układ rozumiemy pewną sztucznie wydzieloną część świata materialnego, która stanowi obiekt naszych badań.

Otoczenie - wszystko co znajduje się poza układem nazywamy otoczeniem.

Parametry stanu - są to wielkości fizyczne określające stan układu (np. m, V, T, p, stężenie C_i )

Co to jest energia wewnętrzna, co to są funkcje stanu?

Energia wewnętrzna - suma wszystkich rodzajów energii układu, w danych warunkach nazywamy energią wewnętrzną układu i oznaczamy małą literką „u”. Energie wewnętrzną 1mola substancji oznaczamy duża literką „U”. Na całkowitą energię układu, którą nazywać będziemy energią wewnętrzną układu (U) składają się: energia potencjalna i kinetyczna makroskopowych części układu, energia kinetyczna cząstek, energia potencjalna oddziaływań między cząsteczkowych i wewnątrz cząsteczkowych itp.

Funkcja stanu - są to funkcje parametrów stanu określających stan układu. Można nimi jednoznacznie opisać układ.

Omówić pierwszą zasadę termodynamiki.

Pierwsza zasada termodynamiki stwierdza, że energia nie może powstać z niczego, a jedynie może zmieniać się z jedne formy energii w inną. Jeżeli do układu doprowadzimy pewną ilość energii na sposób cieplny Q oraz wykonamy na korzyść układu pracę W (wszystkie pozostałe formy energii) to przyrost energii wewnętrznej układu ΔU wyniesie: ΔU= Q + W

Energia wewnętrzna jest funkcją parametrów stanu, natomiast energia przekazana na sposób ciepła oraz pracy nie są funkcjami stanu, ich wielkość zależy więc od sposobu dokonywania przemian. Ciepło Q doprowadzone do układu oraz pracę W wykonaną na korzyść układu (doprowadzoną do układu) przyjmujemy za dodatnią.

Omówić co to jest entalpia i podać odpowiednie zależności:

Entalpia - podobnie jak energia wewnętrzna, entalpia układu jest jednoznaczną funkcją zmiennych stanu układu.

H = U + pV

Po zróżniczkowaniu równania otrzymujemy:

dH = dU + pdV + Vdp

p=const

dH = dU + pdV

a więc: Q_p = ΔH = ΔU + pdV

Zmiana entalpii układu ΔH równa jest ilości wymienionej energii na sposób cieplny Q_p , gdy proces dokonuje się w stałej temperaturze i pod stałym ciśnieniem. Jeżeli w reakcji, obok ciał stałych i cieczy biorą udział gazy, wtedy zmianę objętości ciał stałych i cieczy można zwykle pominąć jako bardzo małe w stosunku do zmiany objętości gazów. Jeżeli ponadto przyjmuje się, że gazy stosują się do praw gazu doskonałego , to możemy założyć, że pod stałym ciśnieniem i w stałej temperaturze: pΔV = RTΔn_g

Wówczas molowa entalpia reakcji Δ_rH będzie równa: Δ_rH= Δ_rU + RTΔn_g

We wzorze tym Δn_g oznacza zmianę licz moli gazowych reagentów w wyniku reakcji: Δn_g = Σn” - Σn'

Σn” - suma ilości moli produktów gazowych

Σn' - suma ilości moli substratów gazowych

Jak definiuje się ciepło molowe w stałej objętości i pod stałym ciśnieniem ?

Jeżeli do układu o temperaturze T doprowadzimy pod stałym ciśnieniem niewielką ilość energii, to entalpia układu wzrośnie o ðh z temperaturą układu o ðT (jeżeli nie zachodzą w układzie przemiany fazowe). Stosunek przyrostu entalpii do przyrostu temperatury, gdy przyrost temperatury dąży do zera, nazywamy pojemnością cieplną układu C_p , pod stałym ciśnieniem w temperaturze T:

C_p = (ðH / ðT )_p = dQ_p / dT

Podobna zależność zachodzi dla układu w stałej objętości. Pochodną cząstkową energii wewnętrznej względem temperatury w stałej objętości, nazywamy pojemność cieplną układu w stałej objętości C_v :

C_v = (ðU / ðT )_v = dQ_v / dT

Pojemność cieplną 1kg substancji nazywamy ciepłem właściwym i oznaczamy małymi literami c_v i c_p. Jednostką jest dżul na kilogram i kelwin o symbolu [J kg^-1 K^-1]

Pojemność cieplną 1mola substancji nazywamy ciepłem molowym i oznaczamy dużymi literami C_v i C_p. Jednostką jest dżul na mol i kelwin o symbolu [J mol^-1 K^-1]

Wyprowadzić zależność między C_p a C_v dla gazu doskonałego:

dH / dT = dU / dT + d(pV) / dT

dla 1 mola pV = RT

dH / dT = dU / dT + d(RT) / dT = dU / dT + R

dH / dT = C_p dU / dT = C_v

stąd: C_p = C_v +R

R = C_p - C_v

Omówić energię i entalpię reakcji.

Z reakcją wiąże się zmiana energii wewnętrznej reakcji i entalpii

aA + bB cC + dD

Zmiana molowej wewnętrznej energii reakcji wynosi:

Δ_rU = d*U_D + c*U_c - b*U_b - a*U_a T = const

Δ_rU = U _produktów - U _substratów = Q_V,T

Zakładamy, że układ reakcyjny przereaguje całkowicie do końca. Stan końcowy - w równowadze niema substratów, przereagowały do końca.

Molowa entalpia reakcji:

Δ_rH = d*H_D + c*H_c - b*H_b - a*H_a

Δ_rH = H _produktów - H _substratów = Q_p,T

Wszystkie reakcje chemiczne związane są z efektami cieplnymi. Entalpia reakcji może być dodatnia albo ujemna.

Jeżeli Δ_rU < 0 lub Δ_rH < 0 oznacza to, że z układu zostało odprowadzone ciepło (wydziela się ciepło) zachodzi reakcja egzotermiczna.

Jeżeli Δ_rH < 0 lub Δ_rU < 0 oznacza to, że z układu pobiera ciepło z otoczenia (przyjmuje ciepło) zachodzi reakcja endotermiczna.

Podaj zależność między energią wewnętrzną a entalpią reakcji.

dH = dU + pdV + Vdp

gdy p = const,

Δ_rH = Δ_rU + pΔV

ΔV - jest to zmiana objętości układu towarzyszącym reakcji. Dla układów skondensowanych (ciekłych lub stałych) o małej objętości: Δ_rH=Δ_rU

Dla gazów zmian ilości moli gazowych reagentów to pΔV = RT Δn_g

Δ_rH = Δ_rU + RT Δn_g

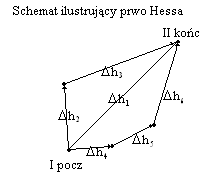
Podać treść i omówić prawo Hessa.

Prawo Hessa stwierdza , że wartości Δu i Δh danego procesu zależą jedynie od stanu początkowego i końcowego układu, a nie zależą od stanów pośrednich, przez które układ przechodzi w czasie trwania procesu.

Rozpatrując przebieg procesu na różnych drogach, raz jako bezpośredni, drugi raz poprzez stany pośrednie, to zgodnie z prawe Hessa wartość Δh (bądź Δu) w obu przypadkach są równe jeśli tylko stan koćowy i początkowy jest taki sam.

Jeżeli procesem jest reakcja chemiczna to wartości Δ_rH i Δ_rU nie zależą od sposobu przeprowadzenia reakcji, lecz jedynie od rodzaju substratów i produktów reakcji. Konsekwencją tego jest możliwość dodawania i odejmowania równań reakcji. Wartości Δ_rH i Δ_rU dodaje się i odejmuje w taki sam sposób, jak równania reakcji, których te funkcję dotyczą. Korzystając z prawa Hessa możemy obliczyć Δ_rh i Δ_ru wielu procesów dla których nie znamy tych wartości, a nawet takich, dla których nie można ich bezpośredni zmierzyć.

Δh₁ = Δh₂ + Δh₃ = Δh₄ + Δh₅ + Δh₆

Podać definicję molowej entalpii spalania, sposób jej wyznaczania i omówić warunki standardowe.

Molowa entalpia spalania jest równa zmianie entalpii układu reakcji całkowitego wpalania w tlenie, jednego mola badanej substancji w warunkach standardowych, przy czym jako produkty spalania powstają CO₂, SO₂, N₂ w stanie gazowym a H₂O w stanie ciekłym.

Entalpie spalania wyznacza się w bombach kalorymetrycznych ( naczynie stalowe o objętości 300 cm³). Do obliczeń termodynamicznych za stan standardowy przyjmuje się z reguły p = 1 atm = 101325 Pa, T = 298,15 K.

Omówić molowe entalpie tworzenia pierwiastków i związków chemicznych/

Molowa entalpia tworzeni pierwiastków. Zostało przyjęte, że dla pierwiastków w stanie czystym w podstawowej przemianie alotropowej wynosi zero, np. Δ_twH⁰_298(grafit) = 0, Δ_twH⁰_298(diament) = 1,895 kJ/mol i Δ_twH⁰_{298(S rombowa)} = 0,

Δ_twH⁰_{298(S jednoskośna)} = 0,297 kJ/mol

Standardowa entalpia tworzenia substancji ( związków chemicznych) - jest róan entalpii reakcji syntezy 1 mola danej substancji pod stałym ciśnieniem p⁰ w temp T = 298,15 substancji prostych w trwałych warunkach syntezy.

Podać definicję i omówić energię wiązania chemicznego.

Standardowa molowa energia wiązania chemicznego jest równa średniej zmianie energii układu podczas procesu w wyniku którego pod stałym ciśnieniem p⁰ w temperaturze 298,15 K w gazowych cząstkach danego związku zostaje zerwany jeden mol określonych wiązań i zostaną utworzone atomy lub rodniki. Jeżeli w cząsteczce zostaną rozerwane wszystkie wiązani powstaje gaz jednoatomowy. Na podstawie energii wiązań można obliczyć w sposób przybliżony entalpię tworzenia takich związków, dla których brak jest danych doświadczalnych. Możemy również na tej podstawie obliczyć entalpie praktycznie dowolnej reakcji.

Wyprowadzić i omówić prawo Kirchoffa.

Δ_rH = H _produktów - H _substratów

(ðΔ_rH / ðT)_p = (ðΔ_rH_prod / ðT)_p - (ðΔ_rH_subs / ðT)_p

(ðH / ðT)_p = C_p

(ðΔ_rH / ðT)_p = C_{p prod} - C_{p subs} = ΔC_{p (regentów)}

(ðΔ_rH / ðT)_p = ΔC_p Δ_rH_T2 = Δ_rH_T1 + _T1∫^T2 ΔC_pdT

(ðΔ_rH / ðT)_V = ΔC_V Δ_rH_T2 = Δ_rH_T1 + _T1∫^T2 ΔC_VdT

C_p - jest to różnica pomiędzy ciepłami molowymi produktów i substratów reakcji, obliczona według równania stechiometrycznego reakcji.

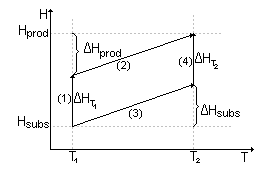
Przedstawić na wykresach zależność entalpii reakcji od temperatury dla reakcji endotermicznej i egzotermicznej.

Zależność entalpii reakcji od temperatury dla reakcji endotermicznej:

(1) + (2) = (3) + (4)

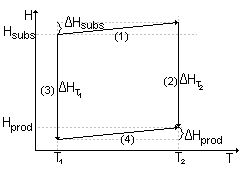
Zależność entalpii reakcji od temperatury dla reakcji endotermicznej

(1)+ (2) = (3) + (4)

Podać przykłady procesów odwracalnych i nieodwracalnych i omówić w jakich warunkach one przebiegają.

Proces odwracalne spełniają następujące warunki:

-układ przechodzi w nim poprzez te same stany pośrednie, co w procesie pierwotnym lecz w odwrotnej kolejności

-układ wymienia z tym procesie z otoczeniem ilości masy, ciepła i pracy różniące się jedyne znakiem od wymienionych w procesie pierwotnym. W ten sposób po zakończeniu proces odwracalnego nie pozostanie żaden ślad ani w układzie, ani w jego otoczeniu. Proces, który nie spełnia chociażby jednego z warunków nazywamy procesem nieodwracalnym. Proces nieodwracalne są to procesy samorzutne.

Dla przemiany odwracalnej zachodzi równość: ΔS = Q_odwr/T

Dla przemiany nieodwracalnej: ΔS > Q_odwr/T

Podać definicję entropii i kilka definicji II zasady termodynamiki.

Entropia jest to funkcja stanu tzn. zmiany jej wartości zależą tylko od początkowego i końcowego stanu układu, a nie od drogi procesu. Entropia służy do określania procesów odwracalnych i nieodwracalnych - jest miarą odwracalności procesów.

dS = dQ_odwrac / T

ΔS _{I , II} = _I∫^II dS = _I∫^II dQ_odwrac / T

Jeżeli T _układu = T _otoczenia to:

dS_układu = dQ_odwrac / T_układu

dS_otoczenia = - dQ_odwrac / T_otoczenia

Różne sformułowania II zasady termodynamiki:

1.Entropia jest funkcją stanu.

2.Łączny przyrost entropii układu i otoczenia może być tylko dodatni lub równy 0

3.Ciepło nie może przechodzić od ciała zimniejszego do cieplejszego

4.Zmiana pracy na ciepło w skutek tarci jest nieodwracalna

5.Czas jest wielkością jednokierunkową.

Podać podstawowe równania reprezentujące I i II zasadę termodynamiki.

II zasda termodynamiki:

Dla przemiany odwracalnej: ΔS = Q_odwr/T

Dla przemiany normalnej: ΔS >= Q_odwr/T

I zasada termodynamiki:

ΔU = Q + W ; dU = dQ + dW ; dU = dQ - pdV ; dQ = dU + pdV

dS >= (dU + pdV) / T ; TdS >= dU +pdV; dU - TdS =< -pdV

T = const to dT = 0

d(U-TS) =< -pdV

Omówić funkcją F zwaną energią swobodną.

Jest to funkcja termodynamiczna, która jest funkcją stanu:

def: F = U - TS

d(U - TS) =< -pdV ; dF =< dW ; ΔF =< W

W przemianie izotermicznej odwracalnej ΔF = W a w przemianie izotermicznej nieodwracalnej ΔF < W. W przemianie izotermiczno -izochorycznej gdy T = const i V = const ΔF =< 0, gdy przemiana jest odrwacalna to ΔF = 0, gdy przemian jest nieodwracalna to ΔF < 0.

Omówić funkcją G zwaną entalpią swobodną.

Entalpia swobodna układu ( zwana też energią swobodną Gibbsa lub potencjałem termodynamicznym)

def: G = H - TS

dU - TdS =< -pdV ; dU - TdS + pdV =< 0

w przemianie izotermiczno- izobarycznej (T,p=const)

d(U + pV - TS) =< 0 , d(H - TS) =< 0 ; dG =< 0

W przemianie izotermiczno - izobarycznej dal procesów odwracalnych ΔG = 0 a dla procesó nieodwracalnych < 0.

Podać i omówić warunki równowagi termodynamicznej.

Równowaga termodynamiczna - jest to taki stan układu w którym w danych warunkach nie zachodzą żadne procesy makroskopowe. Aby układ był w stanie równowagi termodynamicznej muszą być spełnione 3 warunki: Układ musi znajdować się w równowadze termicznej - układ i otoczenie mają taką samą temperaturę, niema różnicy temperatur. Układ znajduje się w stanie równowagi mechanicznej - nie występują w układzie żadne niezrównoważone siły . Układ musi znajdować się w stanie równowagi chemicznej tzn. że muszą być zakończone wszystkie reakcje chemiczne ( układ ma stały skład jakościowy i ilościowy)

Samorzutny: ΔS>0 i rośnie; ΔF < 0 i maleje ; ΔG < i rośnie.

Wyprowadzić wzory różniczkowe na dU i dF ( jako funkcje m.in. entropii S) i wnikające z nich wzory na pochodne cząstkowe.

a) dS = dQ / T ; dQ = TdS; dU = dQ - pdV ; dU = TdS - pdV

jeżeli V = const to (ðU / ðS)_V = T

jeżeli S = const to (ðU / ðV)_S = - p

b) F = U - TS ; dF = dU - TdS - SdT ; dF = TdS - pdV - TdS - SdT;

dF = - SdT - pdV

jeżeli V = const to (ðF / ðT)_V = - S

jeżeli T = const to (ðF / ðV)_T = - p

Wyprowadzić wzory różniczkowe na dH i dG ( jako funkcje m.in. entropii S) i wnikające z nich wzory na pochodne cząstkowe.

a) H = U +pV ; dH = dU + pdV + Vdp ; dH = TdS - pdV + pdV + Vdp

dH = TdS + Vdp

jeżeli p = const to (ðH / ðS)_p = T

jeżeli S = const to (ðH / ðp)_V = V

b) G = H - TS ; dG = dH - TdS - SdT ; dG = TdS + Vdp - TdS - SdT

dG = - SdT + Vdp

jeżeli p = const to (ðG / ðT)_p = - S

jeżeli T = const to (ðG / ðp)_T = V

Wyprowadzić i omówić równania Gibbsa-Helmholtza.

F = U - TS ; G = H - TS

(ðF / ðT)_V = - S ; (ðG / ðT)_p = - S

F = U + T(ðF / ðT)_V ; G = H + T(ðG / ðT)_p

ΔF = ΔU + T(ðΔF / ðT)_V ; ΔG = ΔH + T(ðΔG / ðT)_p

Równania Gibbsa-Helmholotza wyrażają zależność ΔF i ΔG od temperatury.

Podaj równanie entropii jako funkcji temperatury w stałej objętości i pod stałym ciśnieniem.

(ðS / ðT)_V = C_v / T (ðS / ðT)_p = C_p / T

Podać teoremat Nernsta i określić na jakiej podstawie został on sformułowany.

(ðS / ðT)_p = C_p / T jeżeli p=const to dS = (Cp/T)dT

_S0∫^S dS = _T=0∫^T (Cp/T)dT ; S = S₀ + ₀∫^T (Cp/T)dT

S₀ - entropia ciała w temp 0 bezwzględnego

ΔG i ΔH oraz ΔF i ΔU zbliżają się do siebie asymptotyczne gdy temperatura dąży do 0. W temperaturze zera bezwzględnego:

lim _T-0 (ðΔG / ðT)_p = lim _T-0 (ðΔH / ðT)_p = 0

lim _T-0 (ðΔF / ðT)_V = lim _T-0 (ðΔU / ðT)_V = 0

(ðΔG / ðT)_p = - ΔS (ðΔF / ðT)_V = - ΔS

stąd : lim _T-0 ΔS = 0

Teoremat Nernsta - ustala, że różnica entropii produktów i substratów w układach skondensowanych zdążą do zera gdy temperatura zdąża do zera.

Omówić III zasadę termodynamiki, wnioski z niej wypływające i podać przykłady substancji, które nie są ciałami planckowskimi.

Def: Entropia molowa czystych substancji krystalicznych równa jest zeru w temperaturze zera bezwzględnego.

Jeżeli S = 0 bezwzględnemu to ciała takie nazywamy ciałami planckowskimi. Substancjami krystalicznymi , które nie spełniają III zasady termodynamiki są: tlenek węgla CO i tlenek azotu NO.

Wniosek z III zasady termodynamiki:

lim _T-0 ΔC_p = 0

Ciepła molowe wszystkich substancji w zerze bezwzględnym mają wartość zero.

Porównać siły wzajemnego oddziaływania, odległości i stopień uporządkowania cząsteczek w gazach, cieczach i ciałach stałych.

Gazy - gazami nazywamy substancje, które nie wykazują własnego kształtu ani objętości i nie mają swobodnej powierzchni. Siły oddziaływania między cząsteczkowego są znikome, a odległości między cząsteczkami są znaczne. Cząstki poruszają się chaotycznie, zderzają się między sobą, cząstki wypełniają równomiernie całą przestrzeń naczynia w którym się znajdują.

Ciecze - w cieczach cząstki znajdują się bliżej siebie niż w gazach, więc siły oddziaływań między cząstki są większe niż w gazach. Cząstki mogą się swobodnie poruszać, łatwo przybierają kształt naczynia, nie wypełniają całej objętości, mają powierzchnie swobodną.

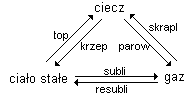
Ciała stałe - cząsteczki są blisko siebie, siły oddziaływania między cząsteczkami są dużo większe niż w cieczach, mają małą swobodę ruchu, cząstki wykonują drgania (tworzą kryształy, ta sama substancja może tworzyć kilka odmian krystalicznych, cząsteczki mają ograniczoną możliwość przesuwania się.

Wszystkie substancje mogą występować jako ciała stałe, gazy i ciecze:

Omówić model gazu doskonałego, prawo Boyle'a - Mariotte'a i prawo Gay - Lussaca.

Podstawowy model gazu doskonałego. Założenia: cząsteczki gazu są punktami materialnymi, cząsteczki nie oddziaływają na siebie wzajemnie, cząsteczki poruszają się ruchem liniowym (prostoliniowym) między zderzeniami, cząsteczki ulegają zderzeniom doskonale sprężystym.

Prawo Boyle'a - Maritte'a:

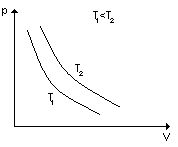
Przemiana izotermiczna. Założenie: nie zmienia się ilośc substancji n=const i T = const czyli pV = const

Wykres izoterm gazu doskonałego w różnych temperaturach

Prawo Gay - Lussaca:

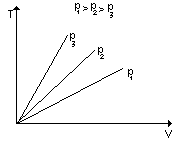
Przemian izobaryczna, założenie n= const i p = const czyli V / T = const

Omówić prawo Charlesa, kombinację praw gazowych i prawo Avogadro.

Przemiana izochoryczna:

Założenie n = const, V = const czyli p/T = const

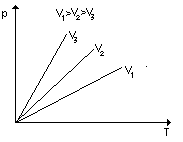
Wykres izochor gazu doskonałego przy różnych objętościach.

Kombinacja praw gazowych: założenie n=const to pV / T = const

Prawo Avogadra - jednakowe objętości różnych gazów w tych samych warunkach ciśnienia i temperatury zawierają jednakową liczbę cząstek. Stała Avogadro (liczba Avogadro) - jest to ilość materii, podaje ile sztuk cząstek odpowiada na 1 mol. Obowiązująca N_A = 6,0221367(36)*10²³ [1/mol] i korygowana (przez IUPAC) N_A = 6,02214199(47)*10²³

Objętość molowa w warunkach T=203,15 i p=p⁰ standardowych V₀ = 0,002241399(4) m³/mol

mol.

Podać i omówić prawo gazu doskonałego i prawo Daltona.

pV = nRT

R - stała gazowa, obowiązująca R = 8,314510(70) J/ (mol*K) i wyrównana R = 8,314472(15) J/ (mol*K), dla gazu doskonałego

R = C_p - C_v

Prawo Daltona - całkowite ciśnienie mieszaniny gazów równe jest sumie ciśnień cząstkowych poszczególnych składników.

p = p₁ + p₂ + p₃ + … = ∑p_i

Ciśnieniem cząstkowym - nazywamy ciśnienie jakie wywierałby dany składnik mieszaniny gdyby on sam wypełniał całą przestrzeń jaką zajmuje mieszanina w danej temperaturze:

p_i = n_i *[ (R*T) / V] p= n₁ *[ (RT) / V] + n₂ *[ (RT) / V] + …

p = (n₁ + n₂ + …) RT/V p = (∑n_i) RT/V

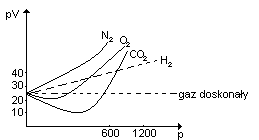
Omówić współczynnik ściśliwości i temperaturę Boyle'a.

Dla gazów rzeczywistych występują następujące oddziaływania.

Dla gazu doskonałego współczynnik ściśliwości z= pV / RT

Dla gazów rzeczywistych „z” jest różne dla różnych gazów i zależy do temperatury:

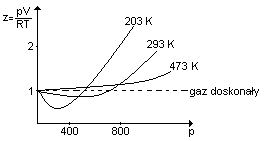
Przy niższych temperaturach maleje współczynnik ściśliwości. Jeżeli z<1 to gaz wykazuje ujemne odchylenie od prawa gazu doskonałego, z>1 to gaz wykazuje dodatnie odchylenie od prawa gazu doskonałego. Dla wszystkich gazów w niskich temperaturach „z” ma wartość <1. Najniższa temperatura powyżej której współczynnik ściśliwości przyjmuje wartość >= 1 nosi nazwę temperatury Boyle'a. Im temperatura Boyle'a jest wyższa tym gaz łatwiej się skrapla. Dla CO₂ temp. Boyle'a = 773 K (łatwo się skrapla), a dla H₂ temp. Bolye'a = 193K (bardzo trudno się skrapla).

Wykazać ile wynosi objętość wyłączona na 1 mol cząsteczek gazu o jednakowych średnicach.

pV = nRT

p(V - nb) = nRT gdzie b- to objętość niedostępna dla jednej cząstki gazu.

4/3 π(2r)³ = 8[4/3 π r³] - objętość wyłączona dla pary cząsteczek

½ *8 [4/3 π r³] = 4 [4/3 π r³] - średnia objętość wyłączona dla jednej cząstki. Jeżeli jest 1 mol cząstek gazu o jednakowych średnicach to objętość wyłączona równa jest : b = 4 [4/3* π r³]*N_A

Podać i omówić równanie wan der Walsa.

Równanie vdV służy do opisywania gazów rzeczywistych przy niskich temperaturach i wyższych ciśnieniach. Wprowadził dwie poprawki do modelu gazu doskonałego (równia stanu gazu doskonałego): uwzględnił objętość własną cząstek, uwzględnił siły przyciągania między cząstkami w gazie.

pV = nRT ; p(V - nb) = nRT ; (p_wew + p_cał)(V - nb) = nRT

p_{wew -} jest proporcjonalne do kwadratu gęstości gazów = a*(n²/V²),

a - stała proporcjonalna

( p + (an²)/V²) ( V - nb) = nRT

Pełne równanie van der Walsa dal gazów rzeczywistych; a, b - stałe zależą od rodzaju gazów ( są różne dla różnych gazów). W granicznych przypadkach kiedy n maleje a V rośnie sprowadza się do równania gazu doskonałego pV = nRT.

Czym różni się równie van der Walsa od równia gazu doskonałego

Wprowadził dwie poprawki do modelu gazu doskonałego (równia stanu gazu doskonałego): uwzględnił objętość własną cząstek, uwzględnił siły przyciągania między cząstkami w gazie.

Podać i omówić inne równania opisujące gazy rzeczywiste poza równaniem wan der Walsa.

Równanie Berthelota - jest to zmodyfikowane równanie wan der Walsa, siły przyciągania nie zleżą tylko od odległości i gęstości ale także od temperatury: ( p + (an²)/TV²) ( V - nb) = nRT

Równanie wirialne - w dowolnych warunkach z dowolną ilością stałych, najprostsza postać: pV = n(RT - Bp)

)

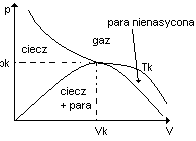
Na wykresie p = f(V) narysować izotermę krytyczną i zanaczyć obszary gazu, pary nienasyconej pary w równowadze z cieczą i cieczy. Podać definicję T_kr, p_kr, V_kr.

Temperatura krytyczna - nazywa się najniższą temperaturę w której gaz nie daje się skroplić lub najwyższej w której daje się skroplić .

Ciśnienie krytyczne - jest to ciśnienie, które jest potrzebne do skroplenia gazu w temperaturze krytycznej.

Objętość krytyczna - jest to objętość jaką zajmuje 1 mol gazu w temperaturze krytycznej i pod ciśnieniem krytycznym.

T_kr, p_kr, V_kr - są charakterystyczne dla każdego gazu ( są podawane w tablicach)

Podać na jakiej podstawie i przy jakich założeniach można powiązać stałe równania van der Walsa z parametrami krytycznymi. Podać takie zależności dla stałych „a” i „b” , bez wyprowadzania.

Izoterma van der Walsa ma tylko punk przegięcia i można ją przyrównać do izotermy krytycznej i stałe wyrazić za pomocą parametrów krytycznych.

( p + (an²)/V²) ( V - nb) = nRT dla n = 1 mol

( p + a/V²) ( V - b) = RT. Zapisujemy p jako funkcję V i przypisujemy ją do izotermy krytycznej i różniczkujemy .

p = RT / (V - b) - a / V²

dp / dv = 0 i następnie d²p / dv² = 0

Stale wyrażone za pomocą parametrów krytycznych:

a = 3 p_kr V_kr² ; b = 1/3 V_kr ; R = ( 8 p_kr V _kr) / 3T_kr

Podać równanie określające wielkość siły potrzebnej do przesunięcia jednej warstwy gazu względem drugiej. Podać jednostki i wymiar współczynnika lepkości dynamicznej.

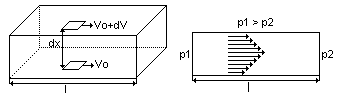
Siła F potrzebna do przesunięcia jednej warstwy gazu względem drugiej

F = η A dV/dx dV - gradient prędkości, dx - gradient powierzchni, η - współczynnik lepkości dynamicznej

F = [N] , η = [N*S / m²], dx = [m²], dV = [m/s]

Lepkość cieczy i gazów wyznacza się za pomocą centypauzów.

1P = 10^-1 N*S/m² ; 1 cP = 10^-3 N*S/m²

Napisz równanie pozwalające na doświadczalne wyznaczenie współczynnika lepkości dynamicznej i równanie pozwalające na jego wyznaczenie za pomocą wielkości charakteryzujących cząsteczkę danego gazu. Od czego zależy a od czego nie zależy lepkość gazów.

Równanie no objętościowy przepływ w rurze

p₁ - p₂ = Δp - różnica ciśnień podczas przepływu. L -długość rury, R - promień rury

V = [(π Δp R⁴ ) / (8 η l)]*t

Lepkość można bezpośredni wyznaczyć z wielkości charakterystycznej danego gazu.

η = 1 / (π δ²) √(mkT / 6) gdzie δ - efektywna średnica cząstek gazu , m - masa cząsteczki gazu k - stał Boltzmana = 1,320685(12)*10^-23 J/K

Ze wzrostem temperatury lepkość gazów rośnie, na odwrót jest przy cieczach, lepkość gazów nie zależy od gęstości ani od ciśnienia, zależy jednak od temperatury.

Podać i omówić praw Ficka.

Równanie na szybkość dyfuzji - I prawo Ficka

dn/dt = - DS dc/dx gdzie : dn/dt - szybkość dyfuzji [ mol/s] ; D - współczynnik dyfuzji [m²/s]; S - powierzchnia prze którą przechodzi dyfuzja [m²]; dc/dx - gradien stęzeń [mol/m⁴]

Równanie dyfuzji - II prawo Ficka

dc/dt = D d²c/dx²

Określić współczynnik dyfuzji za pomocą wielkości charakteryzujących dany gazy. Omówić zjawisko termodyfuzji.

Współczynnik dyfuzji na podstawie wielkości charakteryzujących dany gaz. D = 1/3 ^-u^- * l gdzie D - współczynnik dyfuzji [m²/s]; u - średnia prędkość cząsteczek gazu [m/s] (rośnie ze wzrostem temperatury) l - średnia droga swobodna gazu [m] ( maleje ze wzrostem ciśnienia)

Ze wzrostem temperatury wartość współczynnika dyfuzji rośnie, a ze wzrostem ciśnienia maleje.

Termodyfuzja - jest zjawiskiem zachodzącym po wytworzeniu stałej różnicy temperatur w naczyniu zawierającym dwóch lub więcej gazów. Prowadzi to do wytworzenia różnicy stężeń składników. Zjawisko to jest wykorzystywane do rozdzielania izotopów. .

W wyższej temperaturze następuje gromadzenie się cząsteczek lżejszych a w niższej cięższych .

Omówić zjawisko transfuzji i efuzji. Przedstawić prawo efuzji Grahama.

Transfuzja - przenikanie gazów przez porowate ścianki. Efuzja - przenikanie przez małe otworki.

Kryształ jest płynny jak zazwyczja cieczPrawo efuzji Grahama - w stałej temperaturze i przy stałej różnicy ciśnień, szybkość efuzji różnych gazów są proporcjonalne do pierwiastka kwadratu z gęstości gazów.

ρ = W / V ; W = M ; RT / p ρ=Mp / RT

u₁ / u₂ = √ (M₁p / RT) / (M₂p / RT) = √ M₁/ M₂

Przedstawić na wykresie energię przyciągania, odpychania i ogólnego oddziaływania między cząsteczkami cieczy w zależności od średniej odległości między cząsteczkami.

U₁ - siły przyciągania ; U₂ - siły odpychania ; U - średnia energia oddziaływania między cząsteczkami cieczy

U₁ = - C' / r^{n1 - 1}; U₂ = C” / r^{n2 - 1} ; r₀ - odległość między cząsteczkami jakiejś cieczy w danych warunkach.

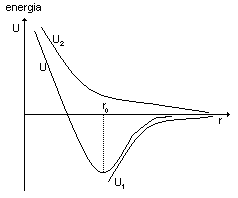
F = - C₁ / rⁿ¹ + C₂ / rⁿ² ; F * r = U

Najmniejsza odległość z jaką cząsteczki się nazywamy promieniem sfery oddziaływania między cząsteczkowego (1*10^-9 m)

Omówić składowe całkowitej energii wiązania van der Waalsa.

Na siły van der Waalsa oddziaływają następujące siły oddziaływania między cząsteczkowego: efekt orientacyjny, efekt indukcyjny, efekt dyspersyjny: U_vdW = U_or + U_ind + U_dys

Efekt orientacyjny - przyciąganie dipol-dipol: U_or = - 2/3 (μ⁴ / r⁶kT)

Efekt indukcyjny - dipol może działać na cząsteczkę sąsiednią i wytwarzać indukcyjny moment dipolowy: U_ind = -2αμ / r⁶

Efekty dyspersyjny (siły dyspersyjne) - wynikają z ruchu elektronów

U_dys = - ¾ (h V₀ α/ r⁶)

μ - trwały moment dipolowy cząsteczki ; k - stała Boltzmana ; r - odległość między cząsteczkami, T - temperatura, α - polaryzowalność cząsteczki, h - stała Plancka ; V₀ - częstotliwość drgań cząsteczek

Omówić wiązanie wodorowe.

Związane jest ze specyficzną budową cząsteczek. Występuje w kwasach, alkoholach, aminach, w związkach gdzie jest wodór i następuje przemieszczenie ładunku O-H, F-H, N-H

Omówić pojęcie lepkości cieczy i równanie Newtona.

F = η A dV/dx , η - współczynnik lepkości dynamicznej,

A - pole przesuwanej warstwy cieczy.

Podać definicję lepkości kinetycznej i wymiary współczynników lepkości dynamicznej i kinetycznej.

Lepkość kinetyczna - jest to stosunek lepkości dynamicznej do gęstości: V = η / ρ

Lepkość kinetyczna jest wyrażana w Stokesach:

Stokes [St] - 10^-4 [m²/s] ; centystokes [cSt] = 10^-6 [m²/s]

Lepkość dynamiczna jest wyrażana w pauzach:

Pauz [P] - 0,1 [Ns/m²] ; centpauz [cP] - 0,001 [Ns/m²]

Omówić równanie Poiseuille'a i równanie Stokes'a.

równanie Poiseuille'a - pozwala na wyznaczenie lepkości dynamicznej

F = 8 π η l V gdzie l - to przepływ kapilarny, V - szybkość przepływu

równanie Stokes'a - pozwala na obliczenie lepkości

F = 6 π η r V gdzie r - promień kulki, a η - lepkość dynamiczna

Wzór na przepływ cieczy prze rurę o długości l, promieniu R i różnicy ciśnień na końcu rury Δp.

V = [(π Δp R⁴ ) / (8 η l) ] *t

Gdy temperatura rośnie, lepkość cieczy maleje, odwrotnie niż w gazach. Lepkość cieczy maleje o 2%, gdy zmniejszymy temperaturę o 1K.

η = A* exp(B/RT)

Omówić napięcie powierzchniowe cieczy i pomiar napięcia powierzchniowego metodą wzniesienia w kapilarze.

Napięciem powierzchniowym nazywamy zjawisko sprężystości powierzchni cieczy, siły zmniejszające powierzchnie cieczy i działające wzdłuż powierzchni cieczy i działające w każdym punkcie (nie zależą od wielkości powierzchni, zależą tylko od rodzaju cieczy i cieczy i temperatury). Żeby zwiększyć powierzchnię cieczy należy wykonać pracę

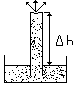
Metoda wzniesienia w kapilarze:

Im mniejsza średnica kapilary to mamy wyższy poziom cieczy Δh. Siła napięcia powierzchniowego działająca na obwodzie.

F = 2π r δ=πr²(h + r/3)g*ξ. Nie da się zmniejszyć promienia kapilary. Dla wody znamy ξ więc policzymy r.

Omówić napięcie powierzchniowe cieczy i pomiar napięcia powierzchniowego metodą stalagmometryczną.

Napięciem powierzchniowym nazywamy zjawisko sprężystości powierzchni cieczy, siły zmniejszające powierzchnie cieczy i działające wzdłuż powierzchni cieczy i działające w każdym punkcie (nie zależą od wielkości powierzchni, zależą tylko od rodzaju cieczy i temperatury). Żeby zwiększyć powierzchnię cieczy należy wykonać pracę.

Metoda stalagmometryczna - kropla odrywa się gdy F napięcia jest równe ciężarowi

Omówić różnice między stanem mezomorficznym a cieczą izotropową i podać jakie substancje wykazują tendencję do tworzenia stanów mezomorficznych.

Niektóre związki organiczne o cząsteczkach płaskich, wydłużonych i zawierających wiązania podwójne lub pierścienie aromatyczne, występują one w pewnym zakresie temperatur w szczególnym stanie fazowym, zwanymi stanem kryształu ciekłego lub fazą mezomorficzną. Ciekłe kryształy są to związki anizotropowe - tworzą mętną ciecz, podwójne załamanie światła. Przy podgrzewaniu tych związków o własnościach anizotropowych dochodzi się do temperatury gdzie ciecz przechodzi w klarowną - staje się cieczą izotropową. W stanie mezomorficznym cząsteczki grupują się w warstwy lub skupiska chociaż są niezależne względem siebie. Obecnie znanych jest ponad 7 tyś ciekłych kryształów. Tendencję wykazują związki organiczne o cząsteczkach płaskich wydłużonych i usztywnionych wiązaniami podwójnymi lub pierścieniem oraz zakończone -COOR , -COR. Najczęściej mają budowę taką:

X - grupa centralna - która decyduje o charakterze związku: -CH=CH- , -C=_C-, -CH=N-, -N=N- , grupa estrowa

estrowa

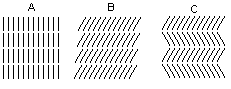
Omówić podział ciekłych kryształów pod względem struktury.

W zależności od uporządkowania cieczy krystalicznej można podzielić na pewne typy, które wykazują jeszcze kilka rodzajów substancji.

Nematyki - cząsteczki ułożone równolegle

Smektyki - kilkanaście rodzajów, najważniejsze a, b, c, uporządkowanie równoległe molekuł w warstwie, są prostopadłe do kolejnej warstwy.

Cholesteryki - mają specyficzne właściwości, są barwne i mają duży współczynnik skręcalności optycznej. Warstwy poziome - jedna jest skręcona względem drugiej o pewien kąt (warstwy są ułożone śrubowo)

Kolumnowy (dyskowy) - typ ten jeszcze nie omawiany w książkach, tworzą się molekuły benzenu z miękkimi podstawnikami.

Każdy z tych typów dzieli się nad podtypy. Mamy 3 rodzaje neomatyków, 2 rodzaje cholesteryków i kilkanaście smektyków.

Podać przykłady zastosowania ciekłych kryształów.

W medycynie do wykrywania raka, wskaźniki cyfrowe, kalkulatory, monitorach, chromatografia gazowa, jako rozpuszczalniki.

Podać równanie określające zmianę entalpii swobodnej ΔG dla dowolnego stadium reakcji gazowej aA + bB cC + dD jako funkcję parcjalnych ciśnień reagentów.

dG = Vdp - SdT T=const

(ðG/ðp)_T = V ; dG=Vdp dal 1 mola gazu doskonałego V = RT/p

dG = RT dp/p ; _G0∫^G dG = RT _p0∫^p p/dp

G - G⁰ = RT ln (p/p⁰)

aA + bB cC + dD

A: aG_A = aG_A⁰ + aRT ln (p_A/p⁰) ; B: bG_B = bG_B⁰ + bRT ln (p_B/p⁰)

C: cG_C = cG_C⁰ + cRT ln (p_C/p⁰) ; D: dG_D = dG_D⁰ + dRT ln (p_D/p⁰)

ΔG = G_prod - G_subs = cG_C + dG_D - aC_A - bC_B

ΔG = cG_C⁰ + dG_D⁰ - aG_A⁰ - bG_B + RT ln [(p_C/p⁰)^c (p_d/p⁰)^d / (p_a/p⁰)^a (p_b/p⁰)^b]

ΔG = ΔG⁰ + RT ln [(p_C/p⁰)^c (p_d/p⁰)^d / (p_a/p⁰)^a (p_b/p⁰)^b]

Podać warunek stanu równowagi reakcji (wartość ΔG) oraz związek pomiędzy stałą równowagi reakcji i standardową entalpią swobodną (izoterma van't Hoffa).

Jeżeli zachodzi równowaga to ΔG = 0

ΔG⁰ = - RT ln [(p_C/p⁰)^c (p_d/p⁰)^d / (p_a/p⁰)^a (p_b/p⁰)^b]

K = [(p_C/p⁰)^c (p_d/p⁰)^d / (p_a/p⁰)^a (p_b/p⁰)^b]

ΔG⁰ = - RT lnK - izoterma van't Hoffa wiążę nam statykę chemiczną z termodynamiką.

Podaj treść i ogólną postać prawa działania mas.

Prawo działania mas mówi, że substancje reagują tak długo, dopóki stosunek iloczynu stężeń molowych produktów do iloczynu stężeń molowych substratów ( które występują w potęgach wynikających z równania chemicznego) nie osiągnie w stałej temperaturze, stałej wartości K, zwanej stałą równowagi chemicznej.

K = [(p_C/p⁰)^c (p_d/p⁰)^d / (p_a/p⁰)^a (p_b/p⁰)^b]

Wyprowadzić zależność stałej równowagi reakcji od temperatury (izobara van't Hoffa).

dG = Vdp - SdT ; p=const

(ðG/ðT)_p = - S (ðΔG/ðT)_p = - ΔS

ΔG = ΔH - TΔS ; ΔS = (ΔH - ΔG)/T

(ðΔG/ðT)_p = (ΔG - ΔH)/T ; p=cons ; dΔG/dT - ΔG/T = - ΔH/T

dΔG/dT - ΔG/T = T d/dt(ΔG/T) ;

T d/dt ΔG T^-1 = T(T^-1 dΔG/dT - ΔG T^-2) = dΔG/dT - ΔG/T

T d/dt(ΔG⁰/T) = - ΔH⁰/T ; d/dt(ΔG⁰/T) = - ΔH⁰/T²

d/dt(-R lnK) = - ΔH⁰/T²

d lnK / dT = ΔH⁰/RT² - izobara van't Hoffa zależność stałej równowagi reakcji od entalpii reakcji w stanie standardowym

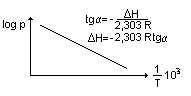
Podać różne postacie równań na zależność stałej równowagi reakcji od temperatury.

∫dlnK = ∫(ΔH⁰ /RT²)dT ; lnK = - (ΔH⁰ / RT) + const

lgK = - (ΔH⁰ / 2,303RT) + const

lg (K₂/K₁) = ΔH⁰ / 2,303R (1/T₁ - 1/T₂)

Podać treść zasady Le Chateliera-Brauna (reguła przekory, zasady przeciwdziałania) i przykłady jej zastosowania.

Jeżeli jest równowaga i zmieniamy warunki układu, to układ zostaje zakłócony. W układzie będzie zachodził proces do osiągnięcia nowej równowagi w nowych zmienionych warunkach równowagowych. Kierunek można określić na podstawie termodynamiki.

Reguła przekory:

Działania zewnętrzne naruszające stan równowagi układu, wywołują w nim takie zmiany, które zmieniają skutki(wyniki) tego działania.

Co to jest faza, liczba faz, niezależny składnik.

Fazą - nazywamy jednorodną pod względem chemicznym i fizycznym część układu oddzielonego od innych części układu wyraźną granicą zwaną granicą fazy.

Liczba faz - oznacza liczbę obecnych w układzie faz.

Składnikami niezależnymi fazy nazywa się te substancje chemiczne, których znajomość wystarcza do określenia składu fazy.

Co to są parametry intensywne, parametry ekstensywne? Podać przykłady.

Parametrami intensywnymi nazywa się wielkości opisujące skład fazy, które nie zależą od stanu fazy np. temperatura, cieśninie, ułamek molowy.

Parametrami ekstensywnymi nazywa się te wielkości zależne od ilości fazy np. objętość, masa.

Podać termodynamiczny warunek równowagi fazowej, ogólną formułę zilustrować dowolnym przykładem.

Równowaga termodynamiczna zostaje osiągnięta, gdy energia swobodna układu uzyska minimum lub gdy potencjały chemiczne składników we wszystkich fazach układu staną się sobie równe. Ustaje wówczas przepływ składników przez granice fazowe z jednej fazy do drugiej.

Podać regułę faz Gibbsa i zdefiniować występujące w niej parametry.

Liczba stopni swobody układu jest to liczba parametrów intensywnych, których wartość można zmienić w pewnych granicach, nie naruszając przy tym warunków równowagi:

S = α - β + 2

S - liczba stopni swobody, α - liczba składników niezależnych faz, β - liczba faz .

Zdefiniować pojecie potencjału chemicznego. Podać i omówić równanie Gibbsa-Duhema.

Potencjał chemiczny u_i jest równy zmianie energii układu podczas zwiększenia liczby moli tego składnika o 1 przy zachowaniu reszty jako stałe - wszystkie inne są niezmienione.

równanie Gibbsa-Duhema : SdT - Vdp + Σn_idu_i = 0

Równanie to wiąże jedną w jedną zależność wielkości intensywne znajdujące się w każdej fazie układu znajdującej się w równaniu.

Podać wzory określające potencjał chemiczny składnika w zależności od składu mieszanin gazowych i składu roztworu. Omówić pojęcie aktywności składnika oraz współczynnika aktywności.

Dla jednego mola gazu w stałej temperaturze:

G = G⁰ + RT ln (p/p⁰) potencjał chemiczny dal i-tego składnika w mieszaninie gazowej: u_i = u_i⁰ + RT ln (p_i/p⁰)

x_i - ułamek molowy i-tego składnika w mieszaninie/ w roztworze

u_i = u_i⁰ + RT lnx_i ; u_i - u_i⁰ = Δu_i = RT lnx_i

Δu_i - zmiana potencjału chemicznego przy przejściu 1 mola i-tego mola składnika ze stanu czystego do roztworu.

Aktywnością składnika a_i w roztworze niedoskonałym nazywamy taką wielkość, która wstawiona w miejsce stężenia w równaniu termodynamicznym , wprowadzony dla mieszanin doskonałych pozwala na obliczenie funkcji termodynamicznych tego składnika.

Współczynnik aktywności f_i - wielkość będąca miarą odstępstwa od doskonałości.

Określić rodzaj układów jednoskładnikowych wielofazowych, które mogą być w równowadze wzajemnej w świetle reguły faz Gibbsa.

para-ciecz, para-ciało stałe, ciecz-ciało stałe, para -ciecz-ciało stałe, ciało stałe (α)-ciało stałe (β), ciecz-ciało stałe(α)-ciało stałe (β),

para-ciało stałe(α)-ciało stałe (β), ciało stałe(α)-ciało stałe (β)- ciało stałe(γ)

Czym jest przemian fazowa a czym jest równowaga fazowa? Co towarzyszy zmianom fazowym?

Przemiana fazowa - to jest zanikanie jednych fazy i zwiększanie się ich kosztem masy innych, a są to np.: parowanie, przemian polimorficzna, rozpuszczanie, krystalizacja.

Stan równowagi fazowej - jest to stan w którym to poszczególne fazy będą współistnieć przez czas dowolnie długi, nie zmieniając swych mas. Zmiany fazowe w układach jednoskładnikowych występują przy zmianie p, T. Przemianom fazowym zawsze towarzyszy efekt cieplny i zmian objętości molowej składnika.

Na podstawie równania Gibbsa-Duhema wyprowadzić równanie Clausiusa-Clapeyrona w postaci ogólnej (poprawnej dla wszelkich przemian fazowych).

u' = u” du' = du”

(S'-S”)dT - (V'-V”)dp = 0 ; ΔSdT - ΔVdp = 0 ;

ΔSdT = ΔVdp ; ΔS = ΔH/T ; dT/dp = ΔV/ΔS

dT/dp = TΔV /ΔH lub dp/dT = ΔH/TΔV

Postać ogólna rówania Clausiusa-Clapyerona jest słuszna zawsze i dotyczy wszelki przemian fazowych

Na podstawie równania Clausiusa-Clapeyrona Gibbsa-Duhema wyprowadzić równanie Clausiusa-Clapeyrona poprawne dla przemian takich jak sublimacja lub parowanie.

V_gaz >> V_ciecz ; V_gaz >> V_{ciało stałe ;} ΔV ≈ V_gaz

ΔV = V_gaz = RT/p _; dp/dT = ΔH/TΔV

dp/dT = ΔHp/RT² ; dp/p = dlnp

dlnp/ dT = ΔH/RT²

Podać i omówić znane postacie równania Clausiusa-Clapeyrona

I postać: dp/dT = ΔH/TΔV

II postać: dlnp/ dT = ΔH/RT²

Zakładamy że ΔH = f(T)

ln p = - ΔH/RT + A

III postać: log p = - (ΔH / 2,303RT )+ A'

_p1∫^p1 dlnp = _T1∫^T1 ΔH/RT² dT

IV postać: ln (p₂/p₁) = ΔH/R (1/T₁ - 1/T₂)

Naszkicować wykres fazowy wody w układzie (p,T) oraz określić za jego pomocą charakterystyczne obszary, linie i punkty.

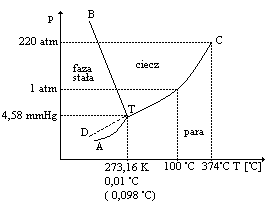
Na każdej krzywej jest tylko jedne stopień swobody. W punkcie potrójnym jest zero stopni swobody, bo ta równowaga zachodzi tylko przy takim ciśnieniu i przy takiej temperaturze. Punkt potrójny wody jest punktem odniesienia w termodynamicznej skali temperatury.

Podać ilość stopni swobody dla charakterystycznych obszarów, linii i punktów wykresu fazowego typowego układu jednoskładnikowego.

Zarówno parametr p i T można w pewnych granicach zmienić nie wywołując przejścia do drugiej fazy. Reguła faz istnieją wtedy 2 stopnie swobody. Zarówno p i T można zmieniać w pewnych granicach, gdy jednak jeden z tych parametrów jest określony, drugi musie mieć wartość wyznaczoną przez linie równowagi. Dla tego przypadku z reguły faz wynika jeden stopień swobody. Na końcu krzywej na wykresie fazowym jest tylko jeden stopień swobody. Wreszcie gdy trzy fazy znajdują się w stanie równowagi reguła faz nie przewiduje istnienia stopni swobody.

Naszkicować wykres fazowy CO₂ w układzie (p,T) oraz określić za jego pomocą charakterystyczne obszary, linie i punkty.

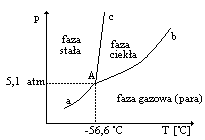
A - punkt potrójny, linia a - zależność prężności pary nasyconej na stałym CO₂ od temperatury, linia b - zależność prężności pary nasyconej nad ciekłym CO₂ , linia c - zależność temperatury topnienia od ciśnienia.

Nachylenie krzywej równowaga ciecz- ciało stałe jest dodatnie. Ciśnienie punktu potrójnego jest bardzo wysokie, konsekwencją tego jest, że pod normalnym ciśnieniem nie można CO₂ pozostać jako ciało bo sublimuje. Przy temperaturze -78,5 ⁰C jest równowaga ciało - stałe gaz.

Naszkicować wykres fazowy siarki w układzie (p,T) oraz określić za jego pomocą charakterystyczne obszary, linie i punkty.

Siarka tworzy 2 odmiany w stanie stałym, na diagramie są trzy punkty potrójne. Są 3 punkty równowagi i jeden neutralny.

1. p=1,4*10³ atm, T = 153,7 ⁰C , 2. p = 3,8*10^-5 atm, T = 119 ⁰C ,

3. 
   p = 1,1*10^-5 atm, T = 95,6 ⁰C, 4. p = 3,5*10^-5 atm, T = 112,8 ⁰C

Podać parametry punku potrójnego wody . Co oznacza on w termodynamicznej skali temperatury. Zdefiniuj zero w skali Celsjusza. Podaj zależność między punktami odniesienia w skali Kelvina i Celsjusza.

Punkt potrójny wody jest punktem odniesienia w termodynamicznej skali temperatury. W punkcie równowagi między trzema fazami zwanym punktem potrójnym występuje współistnienie zwykłego lodu, ciekłej wody i pary wodnej. Zachodzi to pod ciśnieniem 4,58 mmHg i w temperaturze 0,098 ⁰C (273,16K).

Kelwin jest jednostką temperatury termodynamicznej w skali w której temperatura punktu potrójnego wody wynosi 273,16 K. Zero w skali Celsjusza jest zdefiniowane jako temperatura równowagi ludu z wodą (woda nasycona powietrzem) pod ciśnieniem 1 atm. Woda bez rozpuszczonego powietrza krzepnie w temp. 0,0024 ⁰C. W skali Celsjusza zero bezwzględne wynosi - 273,15 ⁰C. Żeby przejść ze skali Celsjusza na skalę Kelvina to dodajemy 273,15.

W jakich przypadkach można rozpatrywać stan równowagi w układzie ciekłym? Podać i scharakteryzować rodzaje takich równowag dla dwóch lub trzech składników.

Układy dwu składnikowe ciekłe o ograniczonej rozpuszczalności (ponieważ nie wszystkie ciecze mieszając się dając układ jednofazowy). Stan równowagi ciecz-ciecz ustala się pod ciśnieniem wyższym niż prężność pary jednej i drugiej cieczy. Możemy rozróżnić 3 rodzaje takich równowag, o górnej temperaturze mieszalności, dolnej mieszalności krytycznej, o dolnej i górnej temperaturze mieszalności.

Przedstawić i omówić wykres fazowy układu dwuskładnikowego ciekłego o ograniczonej rozpuszczalności wzajemnej wykazującą górną temperaturę krytyczna

Zakładamy że ciśnienie jest wyższe od prężności pary nasyconej obu składników - niema pary jest tylko ciecz.

X₁ - punkt poza krzywą, w którym jeden ze związków tworzy roztwór o odpowiednim skaldzie. W punkcie X₂ mieszania nie będzie istnieć jako jedne roztwór ale się rozwarstwi na dwie fazy X₂' i X₂", gdzie X₂' to składnik A nasycony składnikiem B , a X₂" składnikiem B nasycony składnikiem A. Cząstkowe potencjały mają taka samą wartość.

Górna krytyczna temperatura mieszalności - jest to najniższa temperatura powyżej której dane dwie ciecze tworzą układ jednorodny w pełnym zakresie stężeń. np. H₂O - izobutanol

Przedstawić i omówić wykres fazowy układu dwuskładnikowego ciekłego o ograniczonej rozpuszczalności wzajemnej wykazującą dolną temperaturę krytyczną.

Dolna krytyczna temperatura mieszalności - jest to najwyższa temperatura poniżej której dane dwie ciecze tworzą układ jednorodny w pełnym zakresie stężeń. np. H₂O - trójetyloamina

Przedstawić i omówić wykres fazowy układu dwuskładnikowego ciekłego o ograniczonej rozpuszczalności wzajemnej wykazującą jednocześnie dolną i górną temperaturę krytyczną.

np. H₂O - nikotyna, H₂O - metyloetyloketon, pikolina - H₂O, gliceryna - toluidyna

Przedstawić i omówić równowagę ciecz- ciało stałe dwuskładnikowego układu eutektycznego prostego, co nazywamy eutektykiem ?

Eutektykiem nazywamy mieszaninę faz stałych o najniższej i stałej temp. topnienia. np. Cg i Bi, Pb i Ag, Si i Al , KCl i AgCl, benzen i naftalen. Układ eutektyczny dwuskładnikowy prosty - jest to taki układ, który charakteryzuje się całkowitą mieszalnością obu składników w formie ciekłej i całkowitą niemieszalnością w fazie stałej.

Przedstawić i omówić równowagę ciecz- ciało stałe dwuskładnikowego układu wykazującego całkowitą rozpuszczalność wzajemną w fazie ciekłej i stałej w pełnym zakresie stężeń.

Całkowitą rozpuszczalność wzajemna dwóch faz stałych występuje zwykle wówczas gdy stany składników są bardzo zbliżone wielkością i mogą się wzajemnie zastępować w sieci przestrzennej.

Górna krzywa (l z łac. likwidus) określa temperatury w których rozpoczyna się krzepnięcie roztworów o różnych składach. Krzywa dolna (s z łac. solidus) określa skład formy stałej wydzielający się w danej temperaturze krzepnięcia.

Przedstawić i omówić równowagę ciecz- ciało stałe dwuskładnikowego układu wykazującego całkowitą rozpuszczalność wzajemną w fazie ciekłej i stałej w pełnym zakresie stężeń wykazującego minimum temperatury krzepnięcia.

Skład roztworu stałego jest równy składowi cieczy w równowadze

Przedstawić i omówić równowagę ciecz- ciało stałe dwuskładnikowego układu wykazującego całkowitą rozpuszczalność wzajemną w fazie ciekłej i stałej w pełnym zakresie stężeń wykazującego trzy ekstrema temperatury krzepnięcia roztworów stałych.

Wykres dla przypadku A=CCl₄ i B=cykloheksanal,

skład roztworu = skład fazy stałej

Naszkicować i omówić krzywe schładzania (oziębiania) mieszaniny dwóch składników dających eutektyk prosty , dla kilku wybranych stężeń (przykład analizy termicznej).

a - oziębianie cieczy

b - krzepnięcie czystego składnika

c - oziębianie fazy stałej

Krzywe oziębiania przedstawiają nam zmiany temperatury w funkcji czasu.

a - temperatura spada (wydzielanie się składnika), b- krystalizacja składnika znajdującego się w nadmiarze c- krzepnięcie, d- oziębianie fazy stałej w mieszaninie eutektycznej

Analiza termiczna polega na tym że mamy dwa składniki A i B robimy różne mieszaniny i wyznaczamy dla mieszanin krzywe oziębienia - na podstawie czego można zrobić wykres fazowy.

X₄ - eutektyk

Na powierzchni trójkąta równobocznego obrać dowolny punkt i pokazać ja reprezentuje on skład mieszaniny trójskładnikowej.

Jeżeli dowolny punk P znajduje się w polu trójkąta równobocznego to sama jego odległość od boków trójkąta (P_a+P_b+P_c) jest równa wysokości tego trójkąta. Wg Gibbsa wysokość trójkąta równobocznego przedstawia 100% składnika. Procent zawartości składnika A można zmierzyć odległością punktu P, przedstawiającego skład układu, od boku przeciwległego wierzchołka reprezentującego 100% składnika A(R).

Przedstawić za pomocą trójkąta stężeń Gibbsa i omówić wykres fazowy trzech cieczy , których jedna para cieczy wykazuje ograniczoną rozpuszczalność wzajemną.

X_A - głównym składnikiem jest A, który jest wysycany składnikiem B i zawiera pewną ilość składnika C

X_B - głównym składnikiem jest B, który jest wysycany składnikiem A i zawiera pewną ilość składnika C

Układ rozwarstwia się na dwie fazy, te dwie fazy są we wzajemnej równowadze.

Przedstawić za pomocą trójkąta stężeń Gibbsa i omówić wykres fazowy trzech cieczy , których dwie pary cieczy wykazują ograniczoną rozpuszczalność wzajemną.

Dwie pary cieczy wykazują ograniczoną rozpuszczalność: A,C i A,B. Faza złożona ze składników B iC ma nieograniczoną rozpuszczalność wzajemną.

Przedstawić za pomocą trójkąta stężeń Gibbsa i omówić wykres fazowy trzech cieczy , których trzy pary cieczy wykazują ograniczoną rozpuszczalność wzajemną.

Omówić prawo podziału Nerrnsta i wskazać jego zastosowanie.

Mówi o tym że jeżeli mam dwie ciecze o ograniczonej rozpuszczalności to jedna ciecz będzie na dole, druga na górze (lżejsza). Następnie dodając do tego układu trzecią substancje, która rozpuszcza się w obu substancjach. Trzecia substancja rozdziela się między te dwie fazy ciekłe. O tym jak się rozdzieli mówi nam prawo podziału Nernsta.

np.CI₂(w CS₂)/ CI₂(w H₂O) = 625

CI₂(w CH₃Cl)/ CI₂(w H₂O)=120

Ta sama cząsteczka w innych rozpuszczalnikach może mieć inną masę cząsteczkową.

C₁/C₂ⁿ = K prawo podziału Nernsta

n - masa cząsteczkowa substancji rozpuszczonej w (1) rozpuszczalniku do masy cząsteczkowej substancji rozpuszczonej w (2) rozpuszczalniku. Gdy n=1 to stężenie możemy podawać w dowolnych jednostkach, gdy n≠ 1 to stężenie podajemy w mol/dm³ . Prawo to jest wykorzystywane do rozdzielania substancji, gdy w jednym rozpuszczalniku rozpuszcza się lepiej a w drugim gorzej. Ekstrakcja wykorzystuje to prawo.

Omówić prawo Raoulta, narysować i omówić wykres prężności cząstkowych par układu dwuskładnikowego doskonałego.

(2)p_A =x_Ap_A⁰ i (3)p_B =x_Bp_B⁰

Jeżeli para zachowuje się w sposób doskonały można zapisać (1) p=p_A+p_B. W podanych wzorach p_A i p_B prężność par składników A i B nad roztworem zawierającym ułamki molowe x_A i x_B tych składników, natomiast p_A⁰ i p_B⁰ oznaczają prężność par czystych składników. Roztwory spełniające prawo Raoulta określa się jako doskonałe. Zgodnie z bardzie ścisłą definicją mieszaniny składników roztworu doskonałego nie powinna towarzyszyć zmian objętości lub ujemny efekt cieplny.

Omówić równanie Gibbsa - Margulesa, narysować i omówić wykres prężności cząstkowych par układów dwuskładnikowych wykazujących odstępstwa od prawa Raoulta.

(ðlnp_A/ðx_A)_T - (ðlnp_B/ðx_B)_T = 0

Jeżeli znamy prężność par jednego ze składnika nad roztworem, to musimy obliczyć prężność pary drugiego składnika w takiej samej temperaturze. Jeżeli p_rzeczywiste > p_teoretyczne to układ wykazuje dodatnie odchylenie od prawa Raoulta.

Jeżeli p_rzeczywiste < p_teoretyczne to układ wykazuje ujemne odchylenie od prawa Raoulta.

(1) p=p_A+p_B , (2)p_A =x_Ap_A⁰ i (3)p_B =x_Bp_B⁰

Wykazać że jeżeli składnik A jest bardziej lotny niż składnik B to para zawiera więcej składnika A niż ciecz pozsotająća w równowadze z tą parą (dowód że jeżeli p⁰_A > p⁰_B to y_A > x_A)

Tw. Jeżeli składnik A jest bardziej lotny niż składnik B (p⁰_A > p⁰_B) to paraz zawiera więcej składnika A niż ciecz. p⁰_A > p⁰_B ==> y_A > x_A

Z założenia wynika p⁰_A > p⁰_B ==> p⁰_A / p⁰_B >1

y_A/ (1- y_A) = x_A/ (1- x_A) * p⁰_A / p⁰_B czyli

y_A - y_Ax_A > x_A - x_Ay_A

y_A > x_A

Przedstawić na wykresie, dla układu dwuskładnikowego zeotropwego, prężność pary jako funkcję składu roztworu w warunkach izotermicznych (T=cons) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary.

Jeżeli dla dowolnego składu cieczy prężność całkowita pary jest zawarta pomiędzy prężnościami czystych składników, to składniki te nie tworzą mieszani azeotropowych, tzn. są to układy zeotropowe. Mieszaniny zeotropowe - mieszaniny nie wykazujące ekstremum

Przedstawić na wykresie, dla układu dwuskładnikowego tworzącego azeotrop ujemny, prężność pary jako funkcję składu roztworu w warunkach izotermicznych (T=cons) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary.

Podać właściwości mieszanin azeotropowych.

Mieszaniny azeotropowe występują wtedy, gdy ciecze mają zbliżone temperatury wrzenia i wykazują duże odstępstwa od praw Raoulta.

x - para jest bardziej wzbogacona w składnik A niż ciecz

y - para jest bardziej wzbogacona w składnik B niż ciecz

z - dla składu azeotropowego skład pary jest dokładnie taki sam jak skład cieczy.

Przedstawić na wykresie, dla układu dwuskładnikowego tworzącego azeotrop dodatni, prężność pary jako funkcję składu roztworu w warunkach izotermicznych (T=cons) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary.

Podać właściwości mieszanin azeotropowych.

Przedstawić na wykresie, dla układu dwuskładnikowego zeotropwego, temperaturę wrzenia jako funkcję składu roztworu w warunkach izotermicznych (p=cons) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary

Przedstawić na wykresie, dla układu dwuskładnikowego tworzącego azeotrop ujemny, temperaturę wrzenia jako funkcję składu roztworu w warunkach izotermicznych (p=cons) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary.

Podać właściwości mieszanin azeotropowych.

Przedstawić na wykresie, dla układu dwuskładnikowego tworzącego azeotrop dodatni, temperature wrzenia jako funkcję składu roztworu w warunkach izotermicznych (p=const) , określić poszczególne obszary wykresu, podać nazwy linii równowagi i zaznaczyć dla wybranego składu cieczy równowagowy skład pary.

Podać właściwości mieszanin azeotropowych.

Podać warunki jakie spełniają ciecze, które tworzą mieszaniny azeotropowe . Podać właściwości mieszanin azeotropowych; narysować wykresy równowagi izotermicznej lub izobarycznej ciecz - para układów dwu składnikowych , ilustrujące azeotropy dodatnie i ujemne.(patrz pytania wyżej)

Omówić proces destylacji i na wykresie przedstawić przebieg destylacji układu zeotropowego w warunkach izobarycznych.

Destylacja - jest to metoda rozdzielania i czyszczenia ciekłych mieszanin, wykorzystujące różnice lotności składników mieszaniny. Destylacja polega na utrzymywaniu mieszaniny w stanie wrzenia, odparowaniu składników lotnych w danych warunkach ciśnienia i temperatury, ich skroplenia i zebrania w odbieralniku jako tzw. destylat.

Podczas destylacji układu zeotropowego najpierw destyluje składnik o niższej temperaturze wrzenia, a później składnik o wyższej temperaturze wrzenia.

Omówić proces rektyfikacji i na wykresie przedstawić przebieg destylacji układu zeotropowego w warunkach izobarycznych.

Rektyfikacja, destylacja frakcyjna, destylacja frakcjonowana - jest to metoda rozdzielania mieszanin ciekłych na wiele frakcji różniących się składem, przez wielokrotne odparowywanie i skraplanie składników. Rektyfikacja polega na wzbogaceniu par o składniki bardziej lotne dzięki wymianie masy między kierującą się ku górze parze a spływającej w dół cieczy.

Pokazać na wykresie p(T) zjawisko obniżenia temperatury krzepnięcia roztworu w stosunku do krzepnięcia czystego rozpuszczalnika i podać równanie określające wielkość tego efektu.

A - temperatura w której prężność pary nad ciałem stałym i fazą ciekłą jest taka sama. Jest to punkt równowagi ciało stałe-ciecz.

B - temperatura w której prężność pary nad ciałem stałym i rozpuszczalnikiem jest stała, to temperatura krzepnięcia roztwory.

x - ułamek molowy substancji czystej

ΔT = (RT₀² / ΔH_rozp)*x_B

T₀ - temperatura krzepnięcia roztworu, ΔT - obniżenie temperatury roztworu, x_B - ułamek molowy substancji rozpuszczonej, ΔH_rozp - entalpia topnienia rozpuszczalnika

Na podstawie równania Clausiusa - Clapeyrona opisującego proces sublimacji i parowania wyprowadzić zależność no obniżenie temperatury krzepnięcia roztworu od ułamka molowego substancji rozpuszczonej.

dlnp_S / dT = ΔH_sub / RT² ; dlnp⁰ / dT = ΔH_par / RT²

dln(p_s/p⁰) / dT = (ΔH_sub - ΔH_par )/ RT²

ΔH_sub = ΔH_rozp + ΔH_par ; ΔH_rozp = ΔH_sub - ΔH_par

dln(p_s/p⁰) / dT = ΔH_rozp / RT²

w punkcie B p_D=p⁰x ==> x= p_s/p⁰

dlnx/ dT = ΔH_rozp / RT²

_x=1∫^x dlnx = _T0∫^T ΔH_rozp / RT² dT ; gdy x=1 to T=T₀

lnx = - ΔH_rozp / R (1/T - 1/T₀)

zamieniamy x na ułamek molowy substancji rozpuszczonej x_B

ln x = ln (1-x_B) ≈ -x_B gdy x_B jest małe to można to założyć wynika to z ln(1-x) = - (x +x²/2 + x³/3 +…+ xⁿ/n ) -1<x<1

gdy x jest bardzo małe to ln(1-x) = - x

x_B = ΔH_rozp /R (T₀-T / T₀T)

T₀-T = ΔT a gdy T₀ jest małe to T₀T = T²

x_B = ΔH_rozp /R (ΔT / T²)

ΔT = (RT₀² / ΔH_rozp)*x_B

ΔT = (RT₀² / ΔH_rozp)*(n_B/n_A+n_B)

ΔT = (RT₀² / ΔH_rozp)*(b/M_B / aM_A+bM_B)

a>>b to ΔT = (RT₀²b / ΔH_rozp*a*M_B)

Podać równanie pozwalające obliczyć stałą krioskopową rozpuszczalnika i masę cząsteczkową substancji rozpuszczonej na podstawie pomiarów krioskopowych. Omówić wielkości krioskopowe.

K_K = RT₀²/Δh ; ΔT = K_K * (b /a*M_B) ; M_B = K_K*(m_B / m_A*ΔT)

przyjmujemy że b/M_b =n=m (molalność) gdy a=1kg

ΔT = K_K *m

Podać warunki jakie powinien spełniać rozpuszczalnik stosowany do pomiarów krioskopowych oraz równanie pozwalające obliczyć stałą krioskopową rozpuszczalnika.

dobry rozpuszczalnik, nie może wchodzić w reakcje chemiczne z substancjami rozpuszczonymi, powinien mieć małą prężność, dużą stałą krioskopową, nie powinien być toksyczny, przyzwoita temperatura krzepnięcia (-5 ⁰C do 60 ⁰C), nie powinien rozpuszczać jonów ani pary wodnej, nie powinien powodować dysocjacji i asocjacji: K_K = RT₀²/Δh

Pokazać na wykresie p(T) zjawisko (obniżenia prężności pary) podwyższenia temperatury wrzenia roztworu substancji nielotnej w stosunku do temperatury czystego rozpuszczalnika i podać równanie określające wielkość tego efektu .

a - zależność prężności pary nad rozpuszczalnikiem jako funkcja temperatury

b - prężność pary jako funkcja temperatury roztworu

ΔT = (RT₀² / ΔH_parow)*x_B

Wykazać że dla roztworów rozcieńczonych składnika nielotnego względne obniżenie prężności pary jest proporcjonalne do ułamka molowego substancji rozpuszczonej.

p_A=p_A⁰ * x_A ; p_A=p_A⁰ (1 - x_B) ; p_A=p_A⁰ - p_A⁰x_B ; p_A-p_A⁰ ₌ p_Ax_B

x_B =Δp/p

Na podstawie równania Calusius-Clapeyrona wyprowadzić zależność na podwyższenie temperatury wrzenia roztworu substancji nielotnej od ułamka molowego tej substancji.

dlnp / dT = ΔH / RT² ; dlnp = dp/p

dp / pdT = ΔH / RT² dla małych zmian można zastępować przyrostami skończonymi: Δp / pΔT = ΔH / RT² ; x_B =Δp/p

x_B = (ΔH / RT² )* ΔT

ΔT = (RT₀² / ΔH)*x_B

ΔT = (RT₀² / ΔH)*(n_B/n_A+n_B)

ΔT = (RT₀² / ΔH)*(b/M_B / aM_A+bM_B)

a>>b ; ΔH/A= Δh to ΔT = (RT₀²b / Δh*a*M_B)

Podać równanie pozwalające obliczyć stałą ebulioskopową rozpuszczalnika i masę cząsteczkową substancji rozpuszczonej na podstawie pomiarów ebuliskopowych. Omówić wielkość występujące w podanych wzorach.

K_e = RT₀² / Δh ; ΔT = K_e*b / a*M_B ; M_B = K_e*b / a* ΔT

przyjmujemy że b/M_b =n=m (molalność) gdy a=1kg

ΔT = K_e*m

Określić pojęcie krioskopia, ebulioskopia i wskazać zastosowania tych dziedzin.

Krioskopia - metoda bardzo dokładnego pomiaru temperatury krzepnięcia substancji w tzw. kriometrach, zwykle określa się temperaturę krzepnięcia roztworów rozcieńczonych i korzystając z prawa Raoulta wyznacza się masę cząsteczkową związków chemicznych. Stosuje się głownie do badania rozpuszczalności cieczy.

Ebulioskopia - metoda bardzo dokładnego pomiaru temperatury wrzenia w tzw. ebuliometriach. Najczęściej określa się temperaturę wrzenia roztworów rozcieńczonych i korzystając z prawa Raoulta wyznacza się masę cząsteczkową związków chemicznych. Stosuje się głownie do badania stopnia czystości cieczy, rozpuszczalności w azeotropoach.

Na czym polega zjawisko osmozy. Podać równanie na zależność, ciśnienia osmotycznego od ułamka molowego rozpuszczalnika i ułamka molowego substancji rozpuszczonej.

Osmoza - jest to zjawisko polegające na jednokierunkowym przenikaniu (dyfuzji) cząstek rozpuszczalnika prze błoną półprzepuszczalną z roztworu o mniejszy stężeniu do roztworu o większym stężeniu.

πV = - RT lnx₁

πV = - RT ln (1-x₂)

ln(1-x) = - (x +x²/2 + x³/3 +…+ xⁿ/n ) -1<x<1

gdy x jest bardzo małe to ln(1-x) = - x

czyli πV = RT ln x₂

π - ciśnienie osmotyczne ( dodatkowe ciśnienie jakie należy wywrzeć na roztwór oddzielony błoną półprzepuszczalną dla osiągnięcia stężenia równowagowego) V - objętość molowa rozpuszczalnika w roztworze

T - temperatura w której zachodzi równowaga ; x_{2 -} ułamek molowy substancji w roztworze x_{1 -} ułamek molowy rozpuszczalnika w roztworze.

---