Marzena Chmielecka 1

Biotechnologia numer studenta

Wydział Biotechnologii i Nauk o Żywności

Politechniki Łódzkiej

Ćwiczenie nr 15

Wyznaczanie ciepła spalania

Data wykonania ćwiczenia: 03. 10. 2007 r.

Data oddania sprawozdania: 10. 10. 2007 r.

1. Wstęp teoretyczny:

Molowe ciepło reakcji
(lub
) jest to ilość ciepła odniesiona do 1 mola reagenta (substratu lub produktu), wymieniona przez układ z otoczeniem podczas reakcji chemicznej przebiegajacej w następujacycg warunkach:

1. w izobaryczno - izotermicznych P,T = const. (lub izochoryczno - izotermicznych v,T = const),

2. przy całkowitej przemianie substratów w produkty,

3. gdy praca nieobjętościowa jest równa zero.

Prawo Hessa

Prawo Hessa jest podstawowym prawem termochemii:

Molowe ciepło reakcji zależy tylko od rodzaju substratów i produktów, a nie zależy od drogi procesu.

Prawo Hessa umożliwia obliczanie ciepła reakcji na podstawie znanych efektów cieplnych, innych odpowiednich reakcji. Mianowicie, równania termochemiczne można traktować jak równania matematyczne np. dodawać lub odejmować stronami, mnożyć lub dzielić przez dowolną liczbę różną od zera.

Zależność pomiędzy wielkościami
i
, wyraża równanie:

=
(1)

gdzie Δν = c + 1 - a - b jest różnicą sumy współczynników stechiometrycznych produktów i substratów (p. równanie (8.II))

Obliczając różnicę współczynników stechiometrycznych uwzględnia się tylko reagenty w fazie gazowej.

Prawo Kirchoffa

Prawo Kirchoffa podaje zależność molowego ciepła reakcji od temperatury.

dla P = const:
(2)

dla v = const:
(3)

gdzie:

Wielkości
oznaczają molowe pojemności cieplne reagentów. Są to ilości ciepła potrzebne do ogrzania 1 mola substancji o 1 K w warunkach v = const. lub P = const.

Rodzaje kalorymetrów

Podstawowym przyrządem do pomiaru ciepła jest kalorymetr. Jego konstrukcja może być różna. Zasadniczymi jego częściami są (rys.8.2): osłona kalorymetryczna, naczyńko kalorymetryczne z badaną próbką i czujnikiem termometrycznym np. z termometrem rtęciowym. Naczyńko z próbką i czujnikiem nazywa się wewnętrzną cześcią kalorymetru. Zadaniem osłony jest przeciwdziałanie wymianie cieplnej pomiędzy otoczeniem i naczyńkiem z próbką.

Rys. 1. Ogólny schemat kalorymetru. 1 - osłona, 2 - naczyńko kalorymetryczne,

3 - próbka, 4 - czujnik termometryczny T₀ i T_n - temperatury osłony i naczyńka

Brak jest ogólnie przyjętej klasyfikacji kalorymetrów. Często stosowanym jest podział na trzy grupy:

- kalorymetry izotermiczne, w których temperatury osłony T₀ i naczyńka T_n są stałe podczas pomiaru (T₀ = T_n = const., rys..1)

- kalorymetry adiabatyczne, w których temperatury osłony T₀ i naczyńka T_n są sobie równe, lecz zmieniają się podczas pomiaru (T₀ = T_n ≠ const.)

- kalorymetry nieizotermiczne - nieadiabatyczne, w których warunki prowadzenia pomiaru mogą być bardzo różne (T₀ ≠ T_n ≠ const).

W dwóch pierwszych grupach, ze względu na równość temperatur T₀ = T_n , nie ma wymiany ciepła wewnątrz kalorymetru. Nadają się one do pomiaru małych efektów cieplnych.

Przykładem kalorymetru nieizotermicznego - nieadiabatycznego jest bardzo rozpowszechniony kalorymetr diatermiczny (T₀ = const, T_n ≠ T₀). Jego schemat jest podany na rysunku 2.

Rys.2. Schemat kalorymetru diatermicznego dla procesów a) w fazie ciekłej i b) spalania.

A- osłona izolacyjna, B- ciecz kalorymetryczna, D- bagietka do rozbijania ampułek, C- ampułka z badaną substancją, E- mieszadło, F- termomet Beckmana

Służy on do oznaczania ciepła reakcji chemicznych przebiegających w fazie ciekłej, ciepła spalania itd. Osłonę zewnętrzną kalorymetru może stanowić naczynie Dewara, które ma na celu zmniejszyć wymianę ciepła między kalorymetrem a otoczeniem. Naczynie wypełnia się odpowiednią cieczą lub roztworem (cieczą kalorymetryczną). Układ jest wyposażony w mieszadło i czujnik termometryczny. Substraty badanej reakcji znajdują się początkowo: jeden w roztworze (B), a drugi w ampułce szklanej (C).

Rys.3. Schemat bomby kalorymetrycznej

Ciecz kalorymetryczna wraz z wszystkimi zanurzonymi w niej częściami jest odpowiednikiem naczyńka kalorymetrycznego. Zapoczątkowanie reakcji następuje po przebiciu w odpowiednim momencie dna ampułki (C) za pomocą szklanej bagietki (D) lub wrzuceniu kryształka itd. Mieszadło zapewnia zarówno szybkie wymieszanie reagentów jak i utrzymanie równomierności rozkładu temperatury w kalorymetrze. W przypadku pomiaru ciepła spalania zamiast naczynia Dewara stosowana jest osłona metalowa, wewnątrz ktorej umieszcza się bombę kalorymetryczną zamiast ampułki z badanym reagentem.

Schemat bomby został przedstawiony na rys.3. Główną jej częścią jest cylindryczne naczynie z nierdzewnej stali (a) zamykane w górnej części pokrywą (b) i dociskane za pomocą nagwintowanego pierścienia (c). W pokrywie umieszczone są dwa zawory: doprowadzający tlen (e) i odprowadzający gazy po spaleniu (g). Osadzone są także elektrody (d) doprowadzające prąd elektryczny do wnętrza cylindra. Zważoną próbkę badanej substancji w postaci sprasowanej pastylki z umieszczonym w jej środku drucikiem służącym do zapłonu próbki, umieszcza się w naczyńku (f) i podłącza się drucik do elektrod. Do stalowego cylindra wprowadza się tlen pod ciśnieniem około 0,6 MN/m². Przygotowaną w ten sposób do pomiaru bombę zanurza się w wodzie wypełniającej naczynie kalorymetryczne, zaopatrzone w mieszadło i termometr (rys.2b). Całość otoczona jest płaszczem izolacyjnym (osłoną).

2. Pomiary:

Lp.	Czas [s]	Temp. [K]	Czas [s]	Temp. [K]
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

3. Opis wykonywanego ćwiczenia:

Po otrzymaniu pastylki substancji wzorcowej, ważę ją na wadze analitycznej z dokładnością do 0,001 g (waga pastylki 0,952 g). Następnie przystępuję do zestawienia bomby kalorymetrycznej. Głowicę umieszczam w statywie, pastylkę montuję na statywie łącząc końce drucika z elektrodami. Po napełnieniu bomby tlenem naczynie kalorymetryczne napełniam wodą destylowaną, tak aby bomba była całkowicie zanurzona . Po włączeniu zasilania i mieszadła zaczynam mierzyć temperaturę . Spalam próbkę , temperaturę zapisuje co 30s. Po zakończeniu pomiarów wyłączam mieszadło i zasilanie. Wypuszczam gazy spalinowe. Płuczę dolną część bomby wodą destylowaną.

Następnie przystępuję do oznaczania ciepła spalania. W tym celu wykonuję pastylkę z naftalenu, ważę ją (0,882 g) na wadze analitycznej z dokładnością do 0,001 g. Dalsze czynności wykonuje identycznie jak w przypadku wyznaczania pojemności cieplnej bomby kalorymetrycznej .

Pojemność cieplną wyznaczam ze wzoru :

gdzie : K - pojemność cieplna bomby

c - gramowe ciepło spalania

m - masa substancji spalonej

( Δt + Σ ν ) - wyznaczony graficznie przyrost temperatury i poprawka na promieniowanie

Ciepło spalania substancji spalanej wyznaczam z tego samego wzoru po przekształceniu.

4. Obliczenia:

Lp.	Wyznaczanie pojemności cieplnej- temp. (^oC)	Oznaczanie ciepła spalania- temp. (^oC)	Czas (min.)
1.	21,41	23,01	0,0
2.	21,43	23,03	0,5
3.	21,43	23,04	1,0
4.	21,43	23,05	1,5
5.	21,44	23,06	2,0
6.	21,44	23,05	2,5
7.	21,43	23,04	3,0
8.	21,44	23,04	3,5
9.	21,44	23,04	4,0
10.	21,45	23,12	4,5
11.	21,52	23,22	5,0
12.	21,78	23,78	5,5
13.	22,72	24,25	6,0
14.	23,10	24,68	6,5
15.	23,17	24,97	7,0
16.	23,21	25,14	7,5
17.	23,22	25,20	8,0
18.	23,35	25,23	8,5
19.	23,27	25,24	9,0
20.	23,28	25,25	9,5
21.	23,29	25,26	10,0
22.	23,30	25,27	10,5
23.	23,31	25,28	11,0
24.	23,32	25,29	11,5
25.	23,31	25,30	12,0
26.	23,32	25,30	12,5
27.	23,33	25,29	13,0
28.	23,32	25,29	13,5
29.	23,34	25,28	14,0
30.	23,34	25,28	14,5
31.	23,34	25,29	15,0

Masa tabletki wzorcowej: 0,952 g

Masa tabletki z naftalenu: 0,882 g

4. Wyznaczanie pojemności cieplnej bomby kalometrycznej:

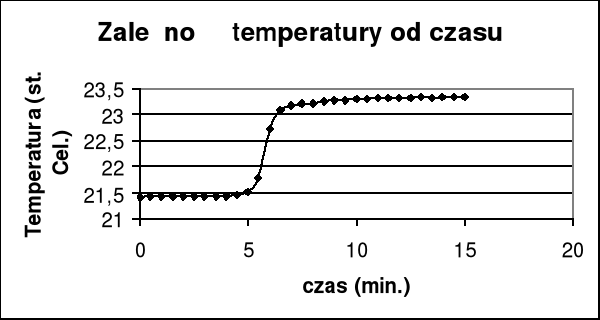
Z wykresu wyznaczam graficznie przyrost temperatury i poprawkę na promieniowanie Δt + Σ ν .

Pojemność cieplną wyznaczam ze wzoru :

Δt + Σ ν =(23,17 - 21,52)= 1,65

czyli pojemność cieplna wynosi :

K= (26,476*0,952)/1,65= 15,276

5. Oznaczanie ciepła spalania :

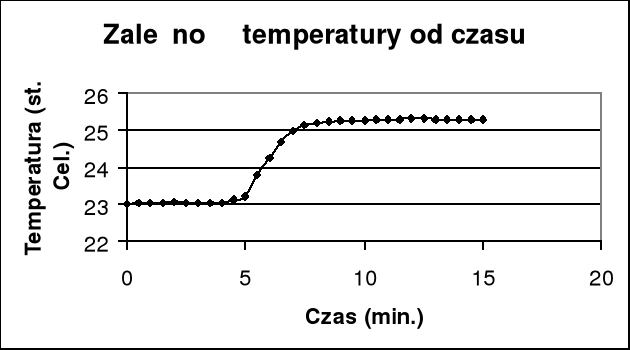
Z wykresu wyznaczam graficznie przyrost temperatury i poprawkę na promieniowanie Δt + Σ ν .

Ciepło spalania obliczam ze wzoru :

Q_sp=K(Δt + Σ ν)/m=(15,276*2,02)/0,882= -34,986 kJ/g

Δt + Σ ν = (25,14 - 23,12) = 2,02

6. Wnioski :

Ciepło spalania oznaczone dla tabletki o wadze 0,882 g ( masa tabletkowa została wzięta ze słoika nr 2 - naftalen ) wynosi -34,986 kJ/g . Jest to wynikiem zmiany energii wewnętrznej spalania ( zachowane warunki procesu w stałej objętości ). Ciepło spalanie ma ujemna wartość ponieważ jest to proces egzotermiczny ( ΔT > 0 ). Ciepło spalania w tablicach wynosi -5157 kJ/mol, zatem obliczone ciepło spalania naftalenu różni się od podanego w tablicach. Wynika to z niedokładności pomiarów, niedokładności wykonanych wykresów i odczytanych z nich wartości. Błąd pomiaru wynika z niedokładności aparatury oraz przenikania ciepła z zewnątrz. Można go wyeliminować stosując dokładniejsza aparaturę pomiarową i dokładniejsze wagi oraz używając lepiej izolowanego zbiornika kalorymetrycznego. W obliczeniach pominięte zostało masa molowa badanej substancji oraz ciepło spalania drucika ( jako mające małą wartość w porównaniu z ciepłem spalania pastylki ). Nachylenie prostych w zakresie okresu końcowego jest skierowane w kierunku liniowo wzrastających temperatur co jest wynikiem ciągłego wzrastania temperatury wody , spowodowanego przepływem ciepła z metalowej konstrukcji bomby kalorymetrycznej. Wartości pomiarów temperatury mogą być obarczone optycznym błędem odczytu.

8

---