Stałe pole elektryczne
Ciała występujące w przyrodzie obdarzone są takimi cechami statycznymi jak masa, objętość, ładunek elektryczny. Pierwsza z nich związana jest z występowaniem pola grawitacyjnego a ostatnia pola elektrostatycznego. W polu grawitacyjnym mieliśmy do czynienia z zasadą zachowania energii-masy. Podobnie w polu elektrostatycznym będziemy obowiązywać zasada zachowania ładunku elektrycznego. W najprostszej postaci mówi ona, że w układzie izolowanym suma skalarna ładunków elektrycznych zawartych w nim ciał jest stała. Oznacza to, że ładunki elektryczne (podobnie jak materia rozumiana jako suma masy i energii) nie mogą ani powstawać ani znikać samoistnie. Choć istnieje zjawisko kreacji par ładunków o przeciwnych znakach z fotonów elektrycznie obojętnych to i to zjawisko jest podporządkowane powyższej zasadzie zachowania ładunku elektrycznego.
Pole elektrostatyczne, podobnie jak pole grawitacyjne jest jednym z tzw. pól oddziaływań. Pole takie charakteryzuje się występowaniem pewnej własności. Cechą taką w przypadku pola grawitacyjnego jest występowanie siły, której wartość jest wprost proporcjonalna do wartości masy próbnika (ciała dostatecznie małego aby nie zakłócać pola wytworzonego przez źródło). W przypadku pola elektrostatycznego próbnik musi posiadać niezerowy ładunek wypadkowy, a siła występująca w tym polu jest wprost proporcjonalna do wartości tego ładunku i zmienia znak na przeciwny przy zmianie znaku ładunku próbnika. Można to symbolicznie zapisać:
1. ∼ q
2. q → -q ⇒ → - .
prawo Coulomba
Dla ładunków punktowych obowiązuje prawo Coulomba:
,
gdzie: oznacza wersor (wektor jednostkowy) skierowany od źródła pola Q do przedmiotu q.
Rys. 38 Siła elektrostatyczna działająca ze strony źródła Q+ na próbnik dodatni q+ w odległości r
zasada superpozycji pól
W przypadku, gdy źródło można podzielić na ładunki punktowe, wypadkowa siłę liczymy sumując wektorowo (!) siły działające na próbnik z ładunkiem i pochodzące od poszczególnych ładunków punktowych źródła Qi.
Siła ta jest ściśle uzależniona od ładunku przedmiotu umieszczonego w polu elektrycznym i będziemy ją traktować jako wektorową cechę tego przedmiotu.
opis skalarny i wektorowy pola elektrostatycznego
Aby wprowadzić wektorową cechę pola elektrostatycznego niezbędne jest określenie wielkości wektorowej niezależnej od q. W tym celu definiujemy „natężenie pola elektrostatycznego :
.
jest więc wielkością wektorową opisującą pole elektrostatyczne.
Jednostką natężenia pola elektrostatycznego jest 1N/1C.
[E] = 1N / 1C
Dla źródła punktowego odpowiedni wzór określający natężenie w odległości r od niego ma postać:
.
Podobnie jak w przypadku sił działających w tym polu stosujemy przy wielu źródłach zasadę superpozycji. Mówi ona, że wypadkowe natężenie pola elektrostatycznego (wypadkowa siła) jest równe wektorowej sumie natężeń (sił) pochodzących od poszczególnych źródeł.
praca w polu elektrostatycznym, potencjał
Podobnie jak w polu grawitacyjnym występuje w polu elektrostatycznym energia potencjalna i potencjał. Założymy, że różnica energii potencjalnej ładunku q przy przemieszczeniu go z odległości rA do odległości rB od źródła (jak na poniższym rysunku) jest równa pracy WA>B siły zewnętrznej równoważącej siłę pola () na tej drodze.
Umowa1: ΔEp = Ep,B - Ep,A = WA>B
Warunek kompensacji tych dwóch sił zabezpiecza nasze rozważania przed zmianą energii kinetycznej próbnika (=0 ⇒ =0 ⇒ =const ⇒ Ek =const ⇒ ΔEk = 0).
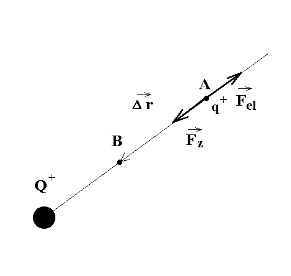
Rys 39 Oddziaływanie ładunków punktowych
Zakładając, że rA > rB i przesuwając próbnik dodatni w kierunku źródła otrzymujemy zgodne zwroty wektorów Δ i co pozwala przedstawić, wykonaną przez siłę zewnętrzną pracę, w postaci:
WA>B = Fz, śr Δr .
Δr jest tu równe (rA - rB) a Fz, śr jest równe średniej geometrycznej wartości początkowej i końcowej siły Fel (Fz = Fel) czyli:
.
Wstawiając do wzoru i przyjmując wartość energii potencjalnej z dokładnością do stałej C otrzymujemy:
Aby określić wartość stałej C wprowadzimy umowę 2.
Umowa2: Ep(∞) = 0
Zakładając, że przesuwamy próbnik z ∞ (rA → ∞) do punktu B otrzymujemy dla punktu A: Ep(∞) = = 0
a stąd wartość C = 0 oraz energię potencjalną próbnika w punkcie B:
.
Tak więc energia potencjalna ładunku w polu elektrostatycznym jest równa pracy jaką wykona siła zewnętrzna równoważąca siłę pola przy przemieszczeniu tego ciała (z ładunkiem) z nieskończoności do danego punktu pola. Z przeprowadzonych wyżej obliczeń wynika, że praca wykonywana przez siły zewnętrzne zależy od początkowej i końcowej odległości r od źródła pola. Wartość pracy przy przesunięciach prostopadłych do kierunku promienia jest równa 0 (cos 90o = 0).
Otrzymaliśmy wielkość skalarną opisującą przedmiot umieszczony w polu elektrostatycznym. Aby otrzymać wielkość skalarną opisującą to pole zdefiniujemy potencjał V:
![]()
.
Potencjałem będziemy więc nazywać wielkość skalarną, której wartość jest równa wartości energii potencjalnej przypadającej na jednostkę ładunku.
Dla źródła punktowego, lub źródła o punktowo symetrycznym rozkładzie gęstości ładunku:
.
Jednostką potencjału elektrycznego jest 1 wolt.
[V] = 1V
Potencjał, analogicznie jak energia potencjalna dla źródła punktowego (ew. źródła o punktowo symetrycznym rozkładzie masy), zależy od różnicy odległości punktu początkowego i końcowego od środka źródła. z tego powodu punkty leżące na sferze kulistej, której środek pokrywa się ze środkiem źródła pola mają ten sam potencjał, a sferę taką nazywamy powierzchnią ekwipotencjalną.
W przypadku wielu źródeł obliczamy potencjał wypadkowy stosując również zasadę superpozycji z tym, że w tym przypadku poszczególne przyczynki sumujemy skalarnie.
Vwyp = ∑ Vi
Z powyższych wzorów można otrzymać związki:
WA>B = q VB - q VA = qU ,
gdzie różnicę potencjałów VB - VA nazywamy napięciem elektrycznym między punktami A i B.
U = VB - VA
Jednostką napięcia elektrycznego jest także 1 wolt.
[U] = 1V
Poniżej przedstawiono w tabeli zestawienie wielkości skalarnych i wektorowych będących cechami przedmiotu i pola elektrostatycznego.
cecha \ wielkość |
skalarna |
wektorowa |
przedmiotu |
Ep - energia potencjalna |
- siła Coulombowska |
pola |
V - potencjał |
- natężenie pola elektrostatycznego |
pojemność elektryczna
Pojemnością elektryczną nazywamy zdolność ciała lub układu ciał do gromadzenia ładunku elektrycznego. Niech ciałem tym będzie przewodnik, na którym zgromadzono ładunek q. Jeśli dzięki temu uzyskał on potencjał V to mówimy, że przewodnik ten posiada pojemność (przewodnika odosobnionego) C:
Codosobnionego = ![]()
(1 farad).
Oprócz pojemności przewodnika odosobnionego występuje pojemność wzajemna przewodników. Jej wartość C obliczamy dzieląc ładunek przeniesiony z jednego przewodnika na drugi przez różnicę potencjałów jaka powstaje wtedy między tymi przewodnikami.
C wzajemna =
Dla kondensatora płaskiego pojemność wzajemną obliczamy z wzoru:
C = ε εo ,
gdzie: εo - przenikalność elektryczna próżni, ε - względna przenikalność elektryczna, S - powierzchnia okładek kondensatora, d - odległość między nimi. Względna przenikalność elektryczna informuje nas ile razy zwiększy się pojemność kondensatora próżniowego po wsunięciu między jego okładki dielektryka (patrz rozdział - przewodniki, izolatory).
Rys. 40 Kondensator płaski
Energię E zmagazynowaną w polu elektrycznym kondensatora obliczamy według poniższego wzoru.
Pojemność elektryczną układu możemy zmieniać, oprócz stosowania dielektryków, przez zmianę odległości jego okładek, zmianę ich powierzchni czynnej (kondensator obrotowy) lub przez łączenie kondensatorów w baterie. Realizujemy to przez połączenia szeregowe lub równoległe.
Rys. 41 Połączenie szeregowe i równoległe kondensatorów
Przy połączeniu szeregowym, zgodnie z zasadą zachowania ładunku elektrycznego sąsiednie, połączone za sobą okładki kondensatorów muszą posiadać ładunki o tej samej wartości i o przeciwnych znakach. Różne wartości pojemności elektrycznej tych kondensatorów powodują istnienie różnych napięć na okładkach tych kondensatorów. Chcąc zastąpić taki układ kondensatorem zastępczym o pojemności CZ musimy uzyskać ten sam ładunek q na jego okładkach i całkowite napięcie C równe sumie napięć U1, U2 i U3.
U = U1 + U2 + U3
Wykorzystując wzór na pojemność elektryczną otrzymujemy:
i po podzieleniu obustronnie przez q :
.
Tak więc odwrotność pojemności elektrycznej baterii kondensatorów połączonych szeregowo jest równa sumie odwrotności pojemności poszczególnych kondensatorów.
W połączeniu równoległym napięcia na wszystkich kondensatorach mają jednakową wartość. Występują różnice ładunków i pojemności. Dla kondensatora zastępczego całkowity ładunek q powinien być równy sumie ładunków q1, q2, q3.
q = q1 + q2 + q3
Wykorzystując wzór e24 otrzymujemy:
C U = C1 U + C2 U + C3 U
i dzieląc ostatnie równanie obustronnie przez U:
C = C1 + C2 + C3 .
Tak więc pojemność zastępcza kondensatorów połączonych równolegle jest równa sumie pojemności poszczególnych kondensatorów.
ruch ładunku w stałym polu elektrycznym
Przeanalizujemy teraz ruch ładunku elektrycznego, np. elektronu w stałym polu elektrycznym. Przybliżeniem takiego pola może być pole elektryczne między okładkami kondensatora płaskiego o dużej wartości pola powierzchni okładek i małej odległości między nimi. Jeśli przyłożymy do niego napięcie U to natężenie pola elektrycznego E między okładkami wyniesie:
Rys. 42 Ruch ładunku w stałym polu elektrycznym
Przedstawiony na powyższym rysunku elektron porusza się wewnątrz kondensatora po parabolicznym torze podobnie jak ciało w rzucie poziomym w polu grawitacyjnym. I podobnie jak w tamtym przypadku można jego ruch rozłożyć na dwa ruchy. Ponieważ w kierunku poziomym nie działają żadne siły dlatego mamy w tym kierunku do czynienia z ruchem jednostajnym prostoliniowym, w którym droga y wyraża się wzorem:
y = v ⋅ t
Jeśli zamiast y wstawimy długość okładek l (drogę w ruchu poziomym w kondensatorze) to wyliczymy z ostatniego wzoru czas t ruchu elektronu między okładkami kondensatora.
Czas ten wykorzystamy do obliczenia odchylenia x toru tego elektronu od kierunku poziomego przy jego wychodzeniu z kondensatora. Ponieważ w kierunku pionowym występuje stałe pole elektryczne E dlatego na elektron będzie działać stała siła o wartości F równej:
F = e E .
Zgodnie z drugą zasadą dynamiki dla ruchu postępowego elektron uzyska przyspieszenie a:
,
oraz:
.
Wykorzystując wzór na drogę w ruchu jednostajnie przyspieszonym:
,
otrzymamy ostatecznie:
.
Widzimy więc, że składowa pionowa x rośnie z kwadratem współrzędnej poziomej l. Oznacza to, że tor jest fragmentem paraboli.
Możemy też wyznaczyć kąt α między kierunkiem wektora prędkości końcowej (wylotu) a poziomem. W tym celu musimy wyznaczyć wartość składowej pionowej wektora prędkości końcowej vy. Skorzystamy z wzoru na prędkość w ruchu jednostajnie zmiennym:
vy = a ⋅ t .
Stąd:
.
Tangens poszukiwanego kąta α jest równy:
,
i ostatecznie:
.
Widzimy więc, że zarówno odchylenie jak i tgα rosną ze wzrostem wartości przyłożonego napięcia U i długości płytek l oraz maleją ze wzrostem odległości płytek d i prędkości v.
Wyszukiwarka
Podobne podstrony:
fiza, rozdz.12-Fale elektromagnetyczne, 12
sccciaga fiza, POLE ELEKTRYCZNE: − Jest polem wektorowym,
fiza, rozdz.9-Prąd elektryczny, 9
fiza, rozdz.9-Prąd elektryczny, 9
Pole elektryczne, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
09 Pole elektryczneid 7817 (2)
1 Pole elektrostatyczne
pole elektromagnetyczne
Pole elektryczne, SZKOŁA
A15 Pole elektryczne w dielektrykach (01 08)
fizyka 7 POLE ELEKTRYCZNE
Pole elektrostatyczne jest to przestrzeń
Pole elektryczne, 8
diatermia, Diatermia kondensatorowa wykorzystuje do nagrzania tkanek pole elektryczne
,fizyka2,pole elektryczne ładunku
Biofizyka moje notatki pole elektromagnetyczne
Pole elektryczne
POLE ELEKTRYCZNE 3(1)
Fizyka Uzupełniająca Pole elektrostatyczne
więcej podobnych podstron