Porządkowanie ciągu elementów, czyli sortowanie
Algorytmy sortujące służą do:
Porządkowania danych,
Umożliwienia stosowania innych algorytmów, np. wyszukiwania,
Lepszej (czytelniejszej dla człowieka) prezentacji danych.
Klasyfikacja algorytmów sortujących
Ze wzglądu na złożoność algorytmy można podzielić na
•proste - wykazują złożoność O(n2) ,
•złożone - logarytmiczne charakteryzuje O(n log n) ~ O(n),
gdzie O( ) oznacza złożoność algorytmu w notacji O.
Zachodzi relacja
O(n2) > O(n log n) > O(n)
Złożoność algorytmu
Określony problem można rozwiązać stosując różne algorytmy. Różnice między algorytmami rozwiązującymi ten sam problem pojawiają się, gdy rośnie liczba przetwarzanych danych. Porównanie algorytmów polega na porównaniu ich złożoności obliczeniowej. Złożoność ogólnie można określić jako ilość pracy potrzebnej do wykonania określonego zadania. Mniejsza ilość pracy oznacza większa wydajność. Wydajność można ocenić na podstawie czasu wykonania i potrzebnej pamięci. Zazwyczaj dla użytkownika istotny jest czas wykonania. Czas zależy od sprzętu, rodzaju programu i struktury algorytmu. Programy kompilowane np. napisane w C++ działają szybciej od interpretowanych, napisanych np. w języku BASIC. Wyznaczenie dokładnej zależności czasu wykonania od ilości danych jest trudne. Dlatego do oceny czasu w zależności od ilości przetwarzanych danych stosuje się miarę zwaną złożonością asymptotyczną, podającą oszacowanie tempa wzrostu czasu wykonania obliczeń. Najpopularniejsza jest notacja Ο (omikron) podana przez Bachmanna w 1894 roku. Spotyka się następujące klasy złożoności:
O(n) W algorytmie występuje liniowa zależność czasu obliczeń od ilości użytych danych. Z każdą daną jest związana stała liczba działań a w związku z tym zwiększenie liczby danych 10 razy wykonania od ilości danych prowadzi do 10 krotnego wzrostu czasu działania.
O(n2) W takim algorytmie wzrost danych 10 razy powoduje wzrost czasu 100 razy. Zjawisko takie występuje, gdy ilość działań wykonanych przez program jest proporcjonalna do ilości danych.
O(n log2 n) Złożoność algorytmu takiej klasy jest uważana za dobrą. Przy 10 danych czas działania jest proporcjonalny do 10log210=33.2. Przy wzroście ilości danych do 100 czas wykonania wzrósł 102 log2102/10log210=20 razy
O(n3), O(2n) Algorytmy o takiej złożoności nie są zalecane.
2. Ze względu na złożoność pamięciową algorytmy dzieli się na:
•sortujące w miejscu
•nie sortujące w miejscu (potrzebna dodatkowa pamięć)
Chodzi tutaj o zapotrzebowanie algorytmu na pamięć. Zapotrzebowanie to określa się przez liczbę koniecznych do działania jednostek pamięci.
Podział ze względu na stabilność
Stabilność polega na utrzymywanie kolejności elementów o tym samym kluczu.
Przykładowe algorytmy sortujące:
Stabilne
Sortowanie bąbelkowe (bubblesort), O(n2),
Sortowanie przez wstawianie (insertion sort), O(n2),
Sortowanie przez scalanie (merge sort), O(n log n),
Sortowanie przez zliczanie (counting sort), O(n + k),
Sortowanie kubełkowe (bucket sort), O(n),
Sortowanie pozycyjne (radix sort) O(n),
Niestabilne
•Sortowanie przez wybór (selection sort) O(n²),
•Sortowanie Shella (shellsort), złożoność nieznana,
•Sortowanie grzebieniowe (combsort), złożoność nieznana,
•Sortowanie szybkie (quicksort), O(n log n),
•Sortowanie introspektywne (introsort), O(n log n),
•Sortowanie przez kopcowanie (heapsort) O(n log n).
Sortowanie bąbelkowe
Sortowanie bąbelkowe to prosty algorytm sortowania o złożoności O(n2).
Algorytm jest mało wydajny i nie stosuje się go do dużych tablic (np. powyżej 1000 elementów).
Sortowanie bąbelkowe polega na porównywaniu dwóch sąsiednich elementów. Jeśli ich kolejność jest niepoprawna to są zamieniane miejscami.
Kod funkcji sortującej
void bubbleSort(int *tablica, int rozmiar)
{
for(int i=1; i<rozmiar ;++i)
for(int j=rozmiar-1; j>=i ;--j)
if(tablica[j] < tablica[j-1])
{
int tmp = tablica[j];
tablica[j]=tablica[j-1];
tablica[j-1]=tmp;
}
}
Schemat blokowy
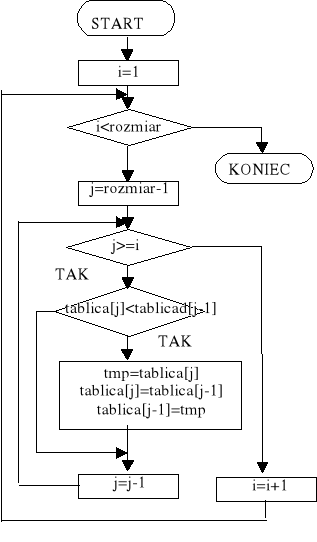
Sortowanie wykonywane jest w dwóch zagnieżdżonych pętlach. Pętla zewnętrzna nr 1 kontrolowana jest przez zmienną j. Wykonuje się ona n - 1 razy. Wewnątrz pętli nr 1 umieszczona jest pętla nr 2 sterowana przez zmienną i. Wykonuje się również n - 1 razy. W efekcie algorytm wykonuje w sumie:
T1(n) = (n - 1)2 = n2 - 2n + 1
obiegów pętli wewnętrznej, po których zakończeniu zbiór zostanie posortowany.
Sortowanie odbywa się wewnątrz pętli nr 2. Kolejno porównywany jest i-ty element z elementem następnym. Jeśli elementy te są w złej kolejności, to zostają zamienione miejscami. W tym miejscu jest najważniejsza różnica pomiędzy algorytmem sortowania bąbelkowego a algorytmem sortowania głupiego. Ten drugi w momencie napotkania elementów o złej kolejności zamienia je miejscami i rozpoczyna cały proces sortowania od początku. Algorytm sortowania bąbelkowego wymienia miejscami źle ułożone elementy sortowanego zbioru i przechodzi do następnej pary zwiększając indeks i o 1. Dzięki takiemu podejściu rośnie efektywność, co odzwierciedla klasa czasowej złożoności obliczeniowej:
Sortowanie głupie - O(n3); Sortowanie bąbelkowe - O(n2)
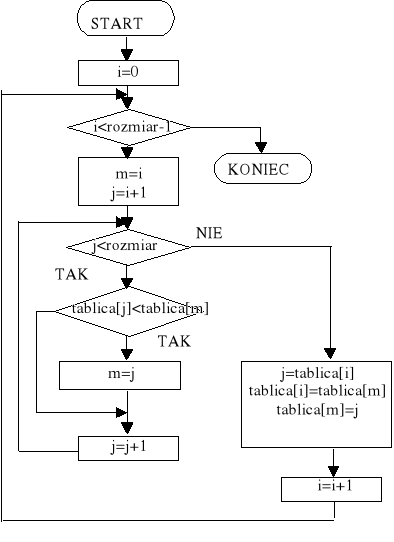
Sortowanie przez wybieranie
Jednym z najprostszych algorytmów sortowania jest sortowanie przez wybieranie (selekcję). Polega ono na wyszukaniu najmniejszego elementu spośród nieposortowanych elementów i ustawieniu go na pierwszej pozycji. Następnie znowu wyszukujemy najmniejszy element i ustawiamy go na drugiej pozycji, itd...
Złożoność obliczeniowa O(n2).
Kod funkcji sortującej
void selectionSort(int *tablica, int rozmiar)
{ int i,j,m;
for(i=0; i<rozmiar-1 ;++i) //od pierwszego elementu do przedostatniego...
{ m = i; //i-ty element przyjmujemy jako najmniejszy
for(j=i+1; j<rozmiar ;++j) //od następnego do ostatniego elementu
if(tablica[j] < tablica[m]) m=j; //jeżeli j-ty jest mniejszy to ...
j = tablica[i]; //ustawiamy element najmniejszy na i-tej pozycji
tablica[i] = tablica[m];
tablica[m] = j;
}
}
Sortowanie przez wstawianie
Sortowanie przez wstawianie należy do prostych algorytmów sortowania o złożoności O(n2).
Polega ono na tym, że bierzemy kolejne elementy do posortowania i wstawiamy je pomiędzy posortowane już elementy na odpowiedniej pozycji.
Weźmy przykładową tablicę o elementach [3,9,5,2,4].
Zaczynamy od drugiego elementu tablicy i sprawdzamy czy jest on mniejszy od elemetu po lewej stronie. Jeśli tak to zamieniamy je miejscami i sprawdzamy następny, aż napotkany element będzie miał wartość mniejszą od obecnie wstawianego.
Po pierwszym kroku 9-tka pozostanie na swojej pozycji, ponieważ nie jest mniejsza od swojego lewego sąsiada.
Teraz bierzemy 5-tke i sprawdzamy czy jest mniejsza od poprzedniego elementu. Ponieważ jest to zamieniamy miejscami te elementy. Następnie sprawdzamy czy znowu 5-tka jest mniejsza od poprzednika - nie jest a więc zostaje na tej pozycji (tablica wygląda tak [3,5,9,2,4]).
Następnie bierzemy kolejny element (2) i dopóki poprzednie elementy są większe od 2 to zamieniamy je miejscami. Tablica zmieni się następująco:
[3,5,9,2,4] -> [3,5,2,9,4] -> [3,2,5,9,4] -> [2,3,5,9,4]
Ostatni element podobnie zamieniamy miejscami z poprzednikami, aż ich wartość będzie niewiększa od wstawianego elementu.
Kod funkcji sortującej
void insertionSort(int *tablica, int rozmiar)
{ for(int i=1; i<rozmiar ;++i)
//od drugiego elementu do ostatniego
{ int tmp = tablica[i];
//zapamietaj wartość elementu
int j=i-1;
//indeks poprzednika
while((j>=0) && (tablica[j]>tmp))
//dopóki istnieje poprzednik
{ //i jego wartość jest większa
tablica[j+1] = tablica[j];
//przesuń poprzedni element w prawo
--j; }
tablica[j+1] = tmp;
//wstaw i-ty element w odpowiednim miejscu
}
}
SZYBKIE SORTOWANIE
Szybkie sortowanie polega na tym, że brany jest pierwszy (w niektórych implementacjach może być inny) element tablicy a następnie jest ustawiany na ostatecznej pozycji. Osiąga się to przerzucając wszystkie mniejsze elementy tablicy na jego lewą stronę, a większe na prawą. Następnie rekurencyjnie sortuje się lewą część tablicy do danego elementu, potem prawą część od danego elementu.
void posortuj(int *tablica, int lewa, int prawa)
{
if (lewa<prawa)
{
int a,m=lewa;
for (int i=lewa+1; i<=prawa; i++)
{
if (tablica[i]<tablica[lewa])
{
m++;
a=tablica[m];
tablica[m]=tablica[i];
tablica[i]=a;
};
};
a=tablica[lewa];
tablica[lewa]=tablica[m];
tablica[m]=a;
posortuj(tablica, lewa, m-1);
posortuj(tablica, m+1, prawa);
}
}
[1] Drozdek A.: C++, Algorytmy i struktury danych. Helion, Gliwice 2004
Wyszukiwarka
Podobne podstrony:
4 sortowanie
Sortowanie cz 2 ppt
cpp 2
cpp z ccfd, pocpp lab7
dane w pigulce 2 cpp
Sortowanie listów
algorytmy sortowanie
5 sortowanie log
Lab3 Cpp GPS opis
4 Sterowanie sortowaniem RSS 2013
borland cpp builder cw10
Ściaga sortowania, algorytmy i struktury danych
Sortowanie kilku kolumn jednocześnie, excel
3 Wyklad Sortowanie
linia sortownicza A1
borland cpp builder cw13
Lab cpp 12
borland cpp builder cw9
więcej podobnych podstron