1

Wykład 5

Sortowanie

w czasie liniowo-

logarytmicznym

2

Sortowanie - zadanie

Definicja (dla liczb):

wejście: ciąg

n

liczb

A

= (

a

1

,

a

2

, …,

a

n

)

wyjście: permutacja (

a

1

,…,

a’

n

) taka, że

a’

1

≤

…

≤ a’

n

3

Zestawienie czasów działania

Ø

 

Przez wybór:

O(N

2

) zawsze

Ø

 

Bąbelkowe:

O(N

2

) najgorszy przypadek; O(N) najlepszy przyp.

Ø

 

Wstawianie:

O(N

2

) średnio; O(N) najlepszy przypadek

Ø

 

Shellsort:

O(N

3/2

)

Ø

 

Heapsort:

O(NlogN) zawsze

Ø

 

Mergesort:

O(NlogN) zawsze

Ø

 

Quicksort:

O(NlogN) średnio; O(N

2

) najgorszy przypadek

Ø

 

Zliczanie:

O(N) zawsze

Ø

 

Radix sort:

O(N) zawsze

Ø

 

zewnętrzne:

O(b logb)) dla pliku o

b

„stronach”.

4

Plan:

Ø

 

Trzy algorytmy sortowania:

Ø

  Mergesort

Ø

  Quicksort

–

 

Bardzo popularny algorytm

,

bardzo szybki w

średnim przypadku

Ø

  Heapsort

–

 

Wykorzystuje strukturę

kopca

(h

eap

)

5

Mergesort – pomysł

Ø

 

Dzielimy ciąg na podciągi, sortujemy te podciągi, a następnie
łączymy zachowując porządek.

–

 

Przykład algorytmu typu „dziel i zwyciężaj”.

–

 

Potrzeba dodatkowego miejsca dla tych podciągów – nie jest to

sortowanie „w miejscu”.

•

 

Można realizować ten proces „w miejscu”, ale rośnie stopień
komplikacji.

–

 

Często realizowany jako metoda zewnętrzna

6

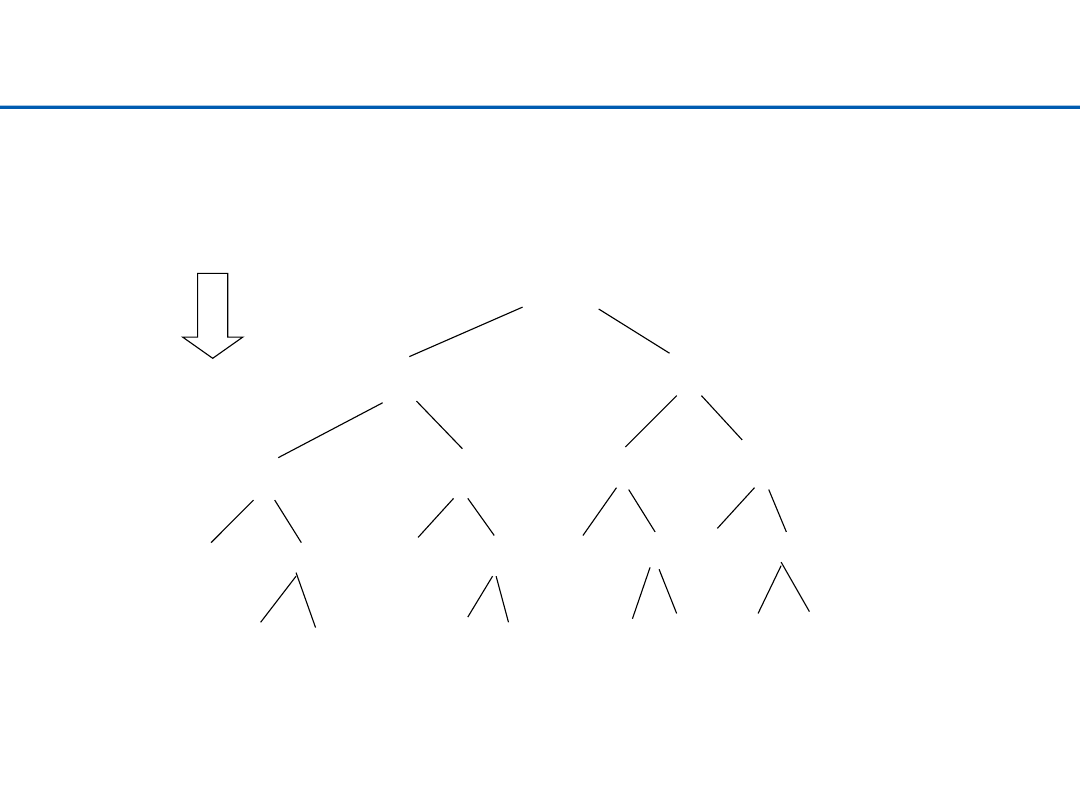
Mergesort – przykład

ciąg: EASYQUESTION (12 znaków)

EASYQUESTION

EASYQU

ESTION

EAS

YQU

EST

ION

E

AS

Y

QU

E ST I ON

A S

Q U

S T

O N

podział

7

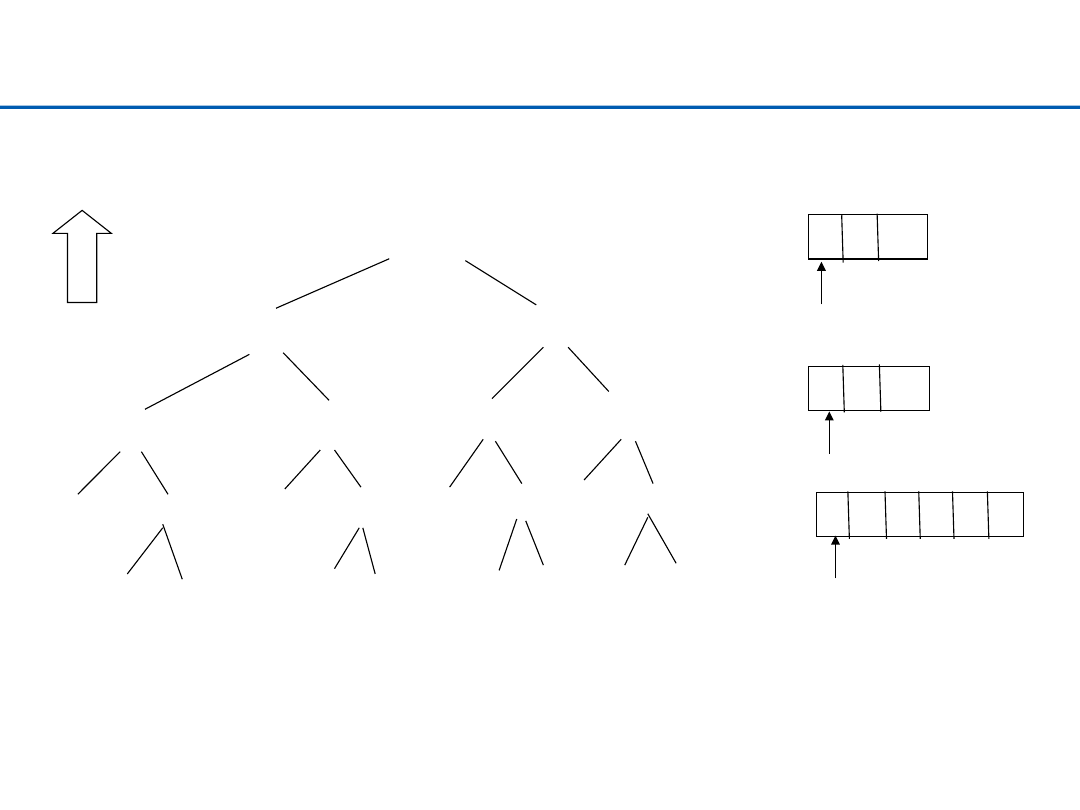
Mergesort – przykład

AEEINOQSSTUY

AEQSUY

EINOST

AES

QUY

EST

INO

E

AS

Y

QU

E

ST

I

NO

A S

Q U

S T

O N

łaczenie

A E S

Q U Y

C1

C2

C3

8

Mergesort - pseudokod

MERGE-SORT(A, p, r)
1 if p < r

2

then q ← ⌊(p + r)/2⌋

3

MERGE-SORT(A, p, q)

4

MERGE-SORT(A, q + 1, r)

5

MERGE(A, p, q, r)

9

Mergesort - pseudokod

MERGE(A, p, q, r)
1 n1 ← q - p + 1
2 n2 ← r - q
3 create arrays L[1 ..n1 + 1] and R[1 ..n2 + 1]
4 for i ← 1 to n1
5 do L[i] ← A[p + i - 1]
6 for j ← 1 to n2
7 do R[j] ← A[q + j]
8 L[n1 + 1] ← ∞
9 R[n2 + 1] ← ∞
10 i ← 1
11 j ← 1
12 for k ← p to r
13 do if L[i] ≤ R[j]
14

then A[k] ← L[i]

15

i ← i + 1

16 else A[k] ← R[j]
17 j ← j + 1

10

Sortowanie szybkie (Quick Sort) - pomysł

Ø

 

Jest to najszybszy w praktyce algorytm sortowania, pozwala na
efektywne implementacje.

–

 

średnio: O(NlogN)

–

 

najgorzej O(N

2

), przypadek bardzo mało prawdopodobny.

Ø

 

Procedura:

–

 

Wybieramy element

osiowy

(

pivot

)

.

–

 

Dzielimy ciąg na dwa podciągi: elementów mniejszych lub równych

od osiowego oraz elementów większych od osiowego. Powtarzamy
takie postępowanie, aż osiągniemy ciąg o długości 1.

–

 

Algorytm typu – „dziel i zwyciężaj”.

–

 

Jest to metoda sortowania w miejscu (podobnie jak I

nsert

-

sort,

przeciwnie do np.

M

erge

-

sort

)

,

czyli nie wymaga dodatkowej

pamięci

11

Quicksort – algorytm

QUICKSORT(A, p, r)
1 if p < r
2 then q ← PARTITION(A, p, r)
3 QUICKSORT(A, p, q - 1)
4 QUICKSORT(A, q + 1, r)

Problemy:

1.

 

Wybór elementu osiowego

;

2.

 

Podział (partition)

.

12

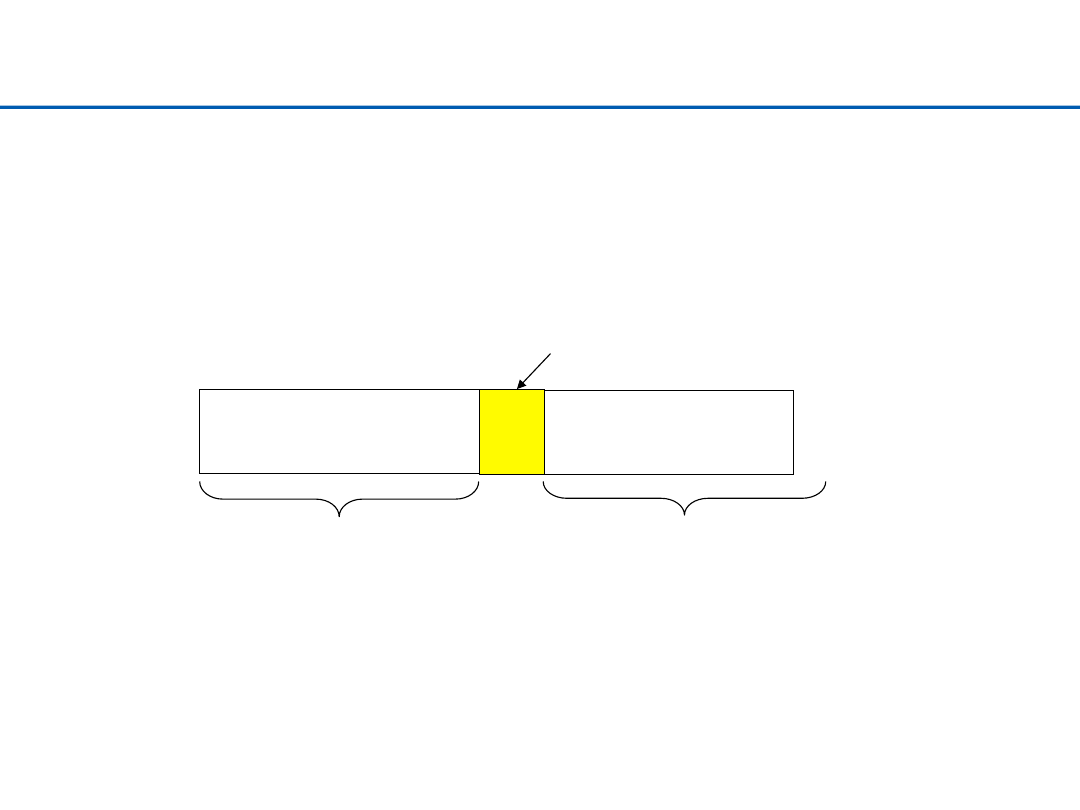
Quicksort – podział

Ø

 

Funkcja

partition

dzieli ciąg na dwa podciągi: elementów

mniejszych (bądź równych) od osiowego i większych od niego

{a[j] | a[j] <= a[i]
dla j ∈[left, i-1]}

{a[k] | a[k] > a[i]
dla k ∈[i+1,right]}

a[i]

wynik

quicksort(a, left, i-1)

wynik

quicksort(a, i+1, right)

Po podziale:

El. osiowy

13

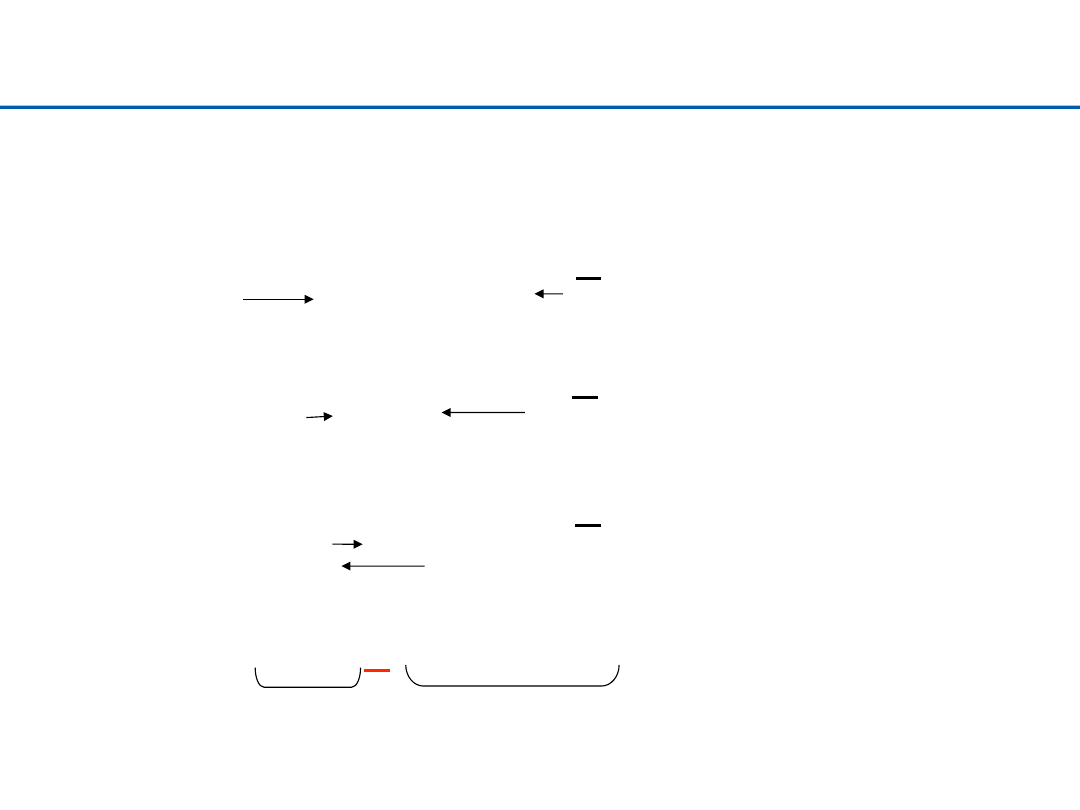
Quicksort – przykład podziału

ciąg: EASYQUESTION (12 znaków).

El. osiowy

: N

E A S Y Q U E S T I O N

Przeglądaj aż: a[i] > a[right]

Przeglądaj aż:

a[j] <= a[right]

i

j

Swap(a[i], a[j])

E A

I

Y Q U E S T

S

O N

i

j

Swap(a[i], a[j])

E A

I

E

Q U

Y

S T

S

O N

i

j

Swap(a[i], a[right])

(indeksy i oraz j „minęły” się)

E A

I

E

N

U

Y

S T

S

O

Q

Lewy podciąg Prawy podciąg

14

Quicksort – wybór elementu osiowego

Ø

 

opcja 1: zawsze wybierać skrajny element (pierwszy lub ostatni).

–

 

Zalety: szybkość;

–

 

Wady: jeśli trafimy na najmniejszy (największy) element podział nie

redukuje istotnie problemu.

Ø

 

opcja 2: wybieramy losowo.

–

 

Zalety: średnio powinno działać dobrze (podział na podciągi o

zbliżonej długości);

–

 

Wady: czasochłonne i nie gwarantuje sukcesu.

Ø

 

opcja 3: wybieramy medianę z pierwszych/ostatnich/środkowych 3/5/7
elementów

.

–

 

gwarantuje, że nie będzie zdegenerowanych podciągów (pustych).

–

 

kompromis pomiędzy opcją 1 i 2

15

Podział – pseudokod (opcja 1)

Partition(A, Left, Right)

1.  Pivot ß A[Right]

2.  i ß Left – 1

3.  for j ß Left to Right–1

4.  do if (A[j] ≤ Pivot)

5.  then i ß i + 1

6.  Exchange(A[i], A[j])

7.  Exchange (A[i+1], A[Right])

8.  return i +1

16

Randomizowany Quicksort (opcja 2)

Ø

 

Zakładamy że nie ma powtórzeń

Ø

 

Jako element osiowy wybieramy losowy element ciągu (opcja 2)

Ø

 

Powtarzamy procedurę, wszystkie podziały są równie prawdopodobne
(1:n-1, 2:n-2, ..., n-1:1), z prawdopodobieństwem 1/n

Ø

 

Randomizacja jest drogą do unikania najgorszego przypadku

17

Randomizowany Quicksort

Randomized-Partition(A,p,r)

01 i←Random(p,r)
02 exchange A[r] ↔A[i]
03 return Partition(A,p,r)

Randomized-Quicksort(A,p,r)

01 if p<r then
02 q←Randomized-Partition(A,p,r)
03 Randomized-Quicksort(A,p,q)
04 Randomized-Quicksort(A,q+1,r)

18

Quicksort – czas działania

Ø

 

Najgorszy przypadek: O(N

2

)

–

 

Podciągi zawsze mają długości 0 i N-1 (el. Osiowy jest zawsze

najmniejszy/największy). Np. dla posortowanego ciągu i pierwszej
opcji wyboru el. osiowego.

Ø

 

Najlepszy przypadek: O(NlogN)

–

 

Podział jest zawsze najlepszy (N/2). El. osiowy zawsze jest

medianą.

Ø

 

Średnio: O(NlogN)

19

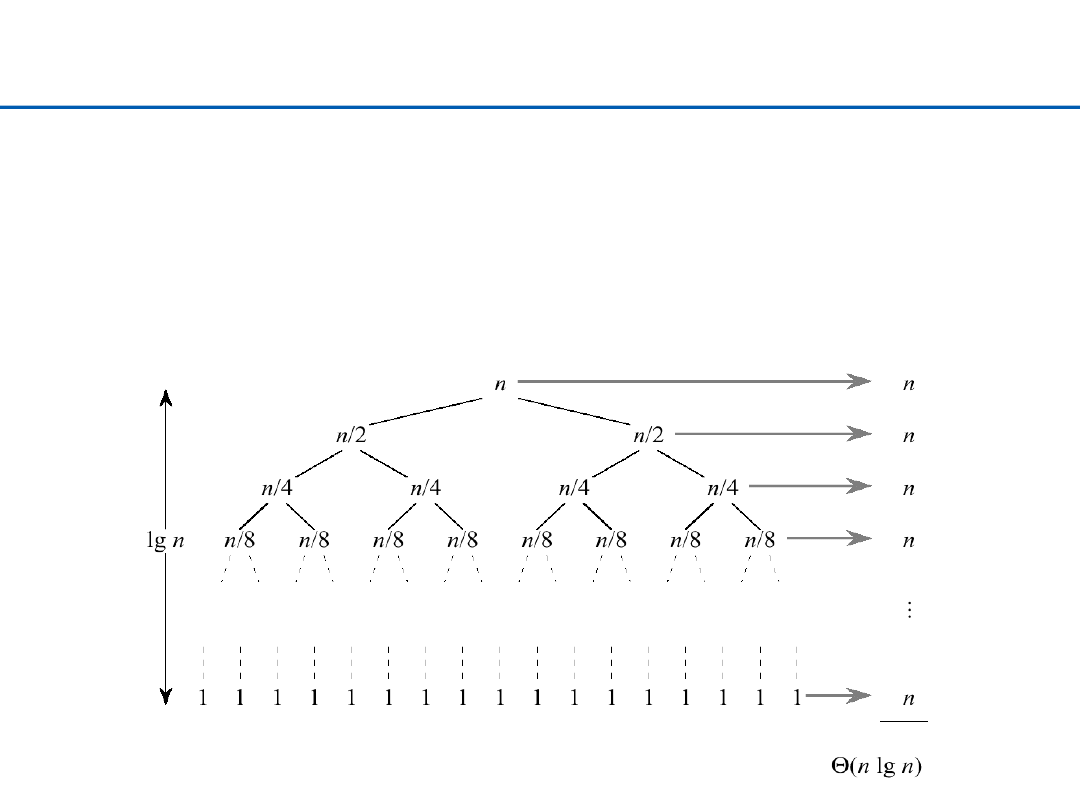
Quicksort – najlepszy przypadek

Ø

 

Podciągi otrzymane w wyniku podziału są równe

( ) 2 ( / 2)

( )

T n

T n

n

=

+ Θ

20

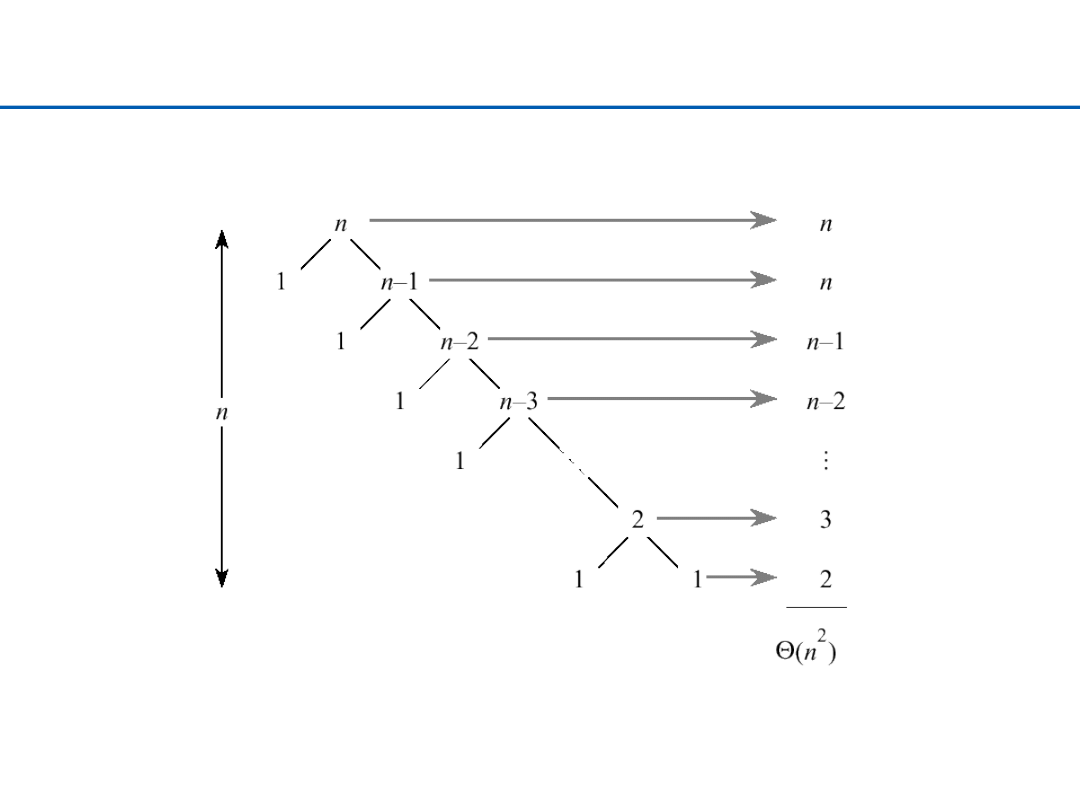
Quicksort – najgorszy przypadek

21

Quicksort- czas działania

Ø

 

T(N) = T(i) + T(N-i-1) + N for N > 1

T(0) = T(1) = 1

–

 

T(i) i T(N-i-1) dla podziału i/N-i-1.

–

 

N dla podziału 1/N-1(liniowe – przeglądamy wszystkie elementy).

22

Quicksort – czas działania

Ø

 

najgorzej: T(N) = T(0) + T(N-1) + N = T(N-1) + N = O(N

2

)

Ø

 

najlepiej: T(N) = 2T(N/2) + N = O(NlogN)

Ø

 

„średnio”:

T(N) = (1/N)

∑

i=0

N-1

T(i) + (1/N)

∑

i=0

N-1

T(N-i-1) + N

= (2/N) ∑

j=0

N-1

T(j) + N = O(NlogN)

23

Quicksort - uwagi

Ø

 

Małe ciągi

–

 

Quicksort zachowuje się źle dla krótkich ciągów.

–

 

Poprawa – jeśli podciąg jest mały zastosować sortowanie przez

wstawianie (zwykle dla ciągów o długości 5 ~ 20)

Ø

 

Porównanie z mergesort:

–

 

Oba zbudowane na zasadzie „dziel i zwyciężaj”.

–

 

Mergesort wykonuje sortowanie w fazie łączenia.

–

 

Quicksort wykonuje prace w fazie podziału.

24

Heap Sort – pojęcie kopca

Ø

 

Struktura kopca binarnego

–

 

Drzewo binarne (bliskie zrównoważenia)

•

 

Wszystkie poziomy, z wyjątkiem co najwyżej ostatniego, kompletnie
zapełnione

–

 

Wartość klucza w węźle jest większa lub równa od wartości kluczy

wszystkich dzieci; własność taka jest zachowana dla lewego i prawego
poddrzewa (zawsze)

25

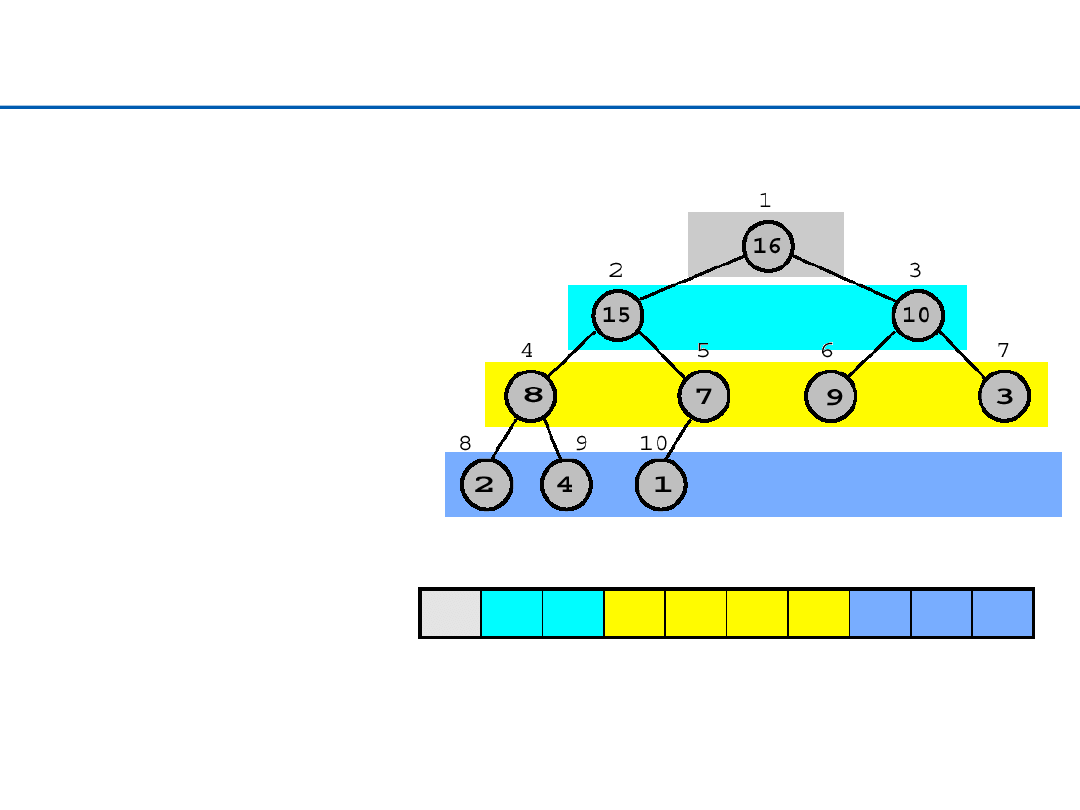
Heap Sort – reprezentacja tablicowa kopca

1

2

3

4

5

6

7

8

9

10

16

15

10

8

7

9

3

2

4

1

Parent (

i

)

return ⎣

i

/2⎦

Left (

i

)

return 2

i

Right (

i

)

return 2

i

+1

Własność kopca:

A

[Parent(

i

)] ≥

A

[

i

]

poziomy: 3

2

1

0

26

Heap Sort – reprezentacja kopca w tablicy

Ø

 

Zauważmy połączenia w drzewie – dzieci węzła

i

występują na pozycjach

2

i

oraz 2

i

+1

Ø

 

Czemu to jest wygodne?

–

 

Dla reprezentacji binarnej

,

dzieleniu/mnożeniu przez 2 odpowiada

przesuwanie (szybka operacja)

–

 

Dodawanie jedynki oznacza zmianę najmłodszego bitu (po przesunięciu)

27

Kopcowanie (Heapify)

Ø

 

Niech

i

będzie indeksem w tablicy

A

Ø

 

Niech drzewa binarne Left(

i

) i Right(

i

) będą kopcami

Ø

 

Ale,

A

[

i

] może być mniejsze od swoich dzieci – co powoduje złamanie

własności kopca

Ø

 

Metoda Kopcowania (

Heapify

) przywraca własności kopca dla

A

poprzez

przesuwanie

A

[

i

] w dół kopca aż do momentu, kiedy własność kopca jest

już spełniona

28

Kopcowanie (Heapify)

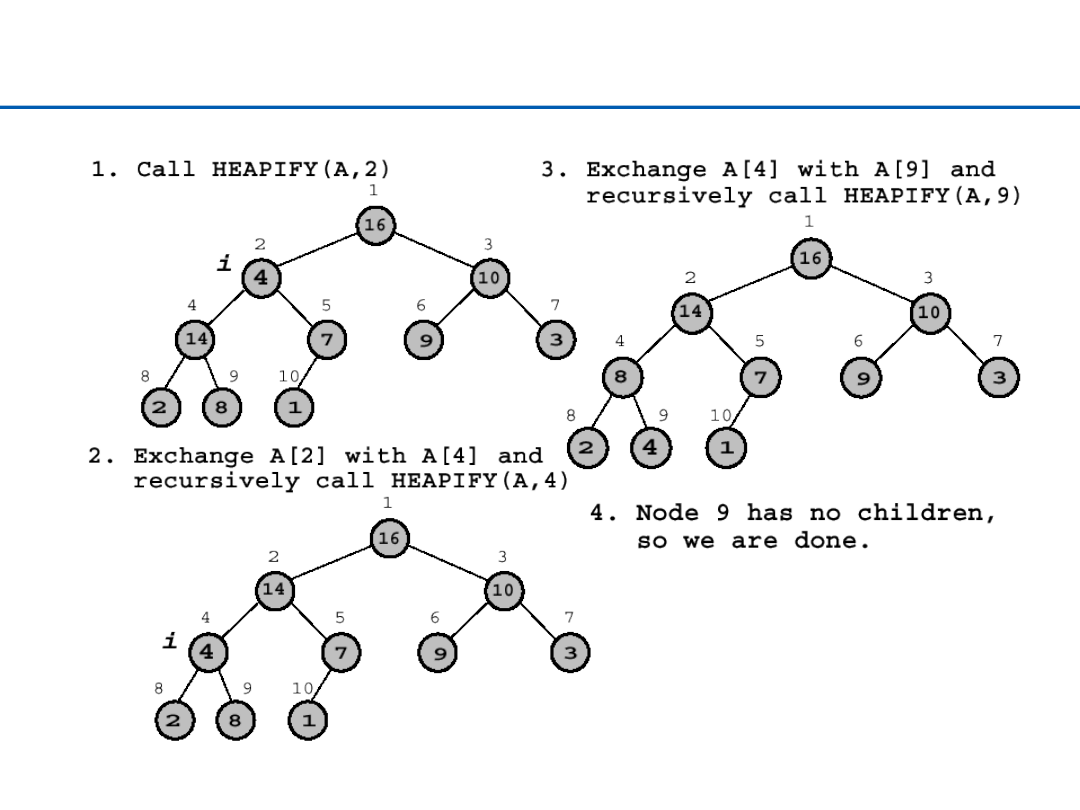
29

Kopcowanie (Heapify) – przykład

30

Kopcowanie – czas działania

Ø

 

Czas działania procedury Heapify dla poddrzewa o

n

węzłach i korzeniu

w

i:

–

 

Ustalenie relacji pomiędzy elementami

: Θ(1)

–

 

dodajemy

czas działania

Heapify

dla poddrzewa o korzeniu w jednym z

potomków

i,

gdzie rozmiar tego poddrzewa

2n/3

jest najgorszym

przypadkiem

.

–

 

Inaczej mówiąc

•

 

Czas działania dla drzewa o wysokości

h: O(h)

( )

(2 /3)

(1)

( )

(log )

T n

T n

T n

O

n

≤

+ Θ

⇒

=

31

Budowa kopca

Ø

 

Konwertujemy tablicę

A

[1...

n

], gdzie

n

= length[

A

], na kopiec

Ø

 

Zauważmy, że elementy w

A

[(

⎣

n/2

⎦

+ 1)...

n

] są już zbiorem kopców -

jednoelementowych!

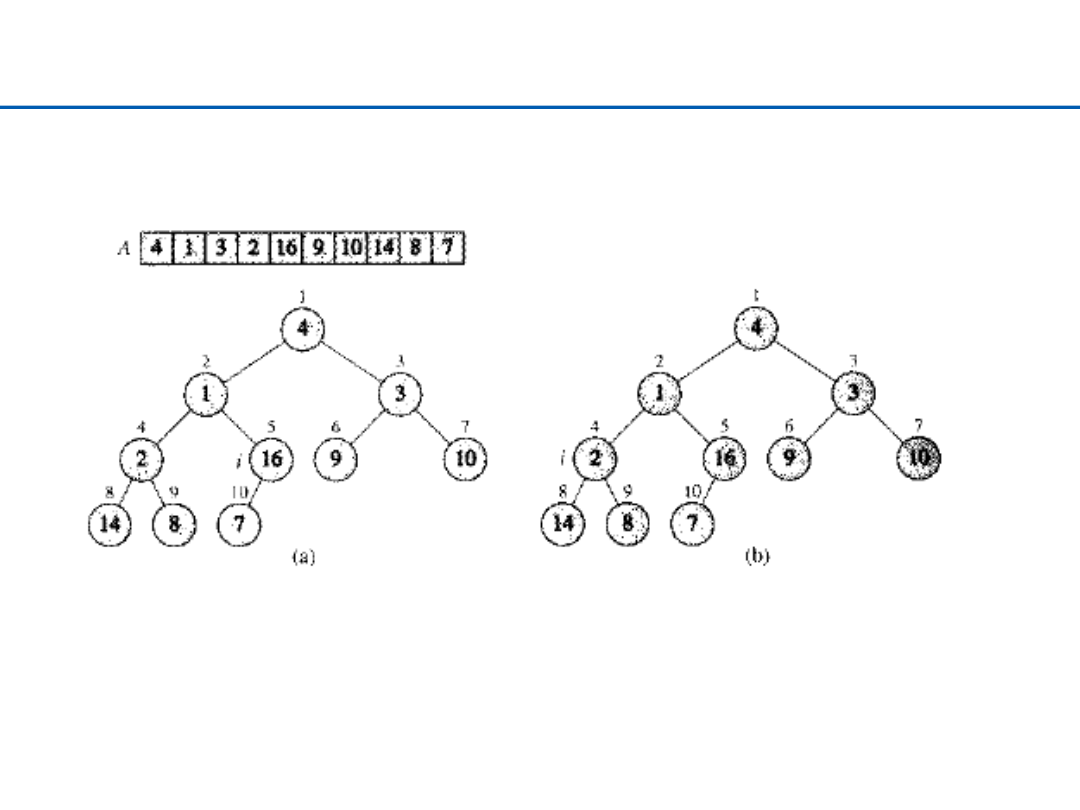
32

Budowanie kopca – 1

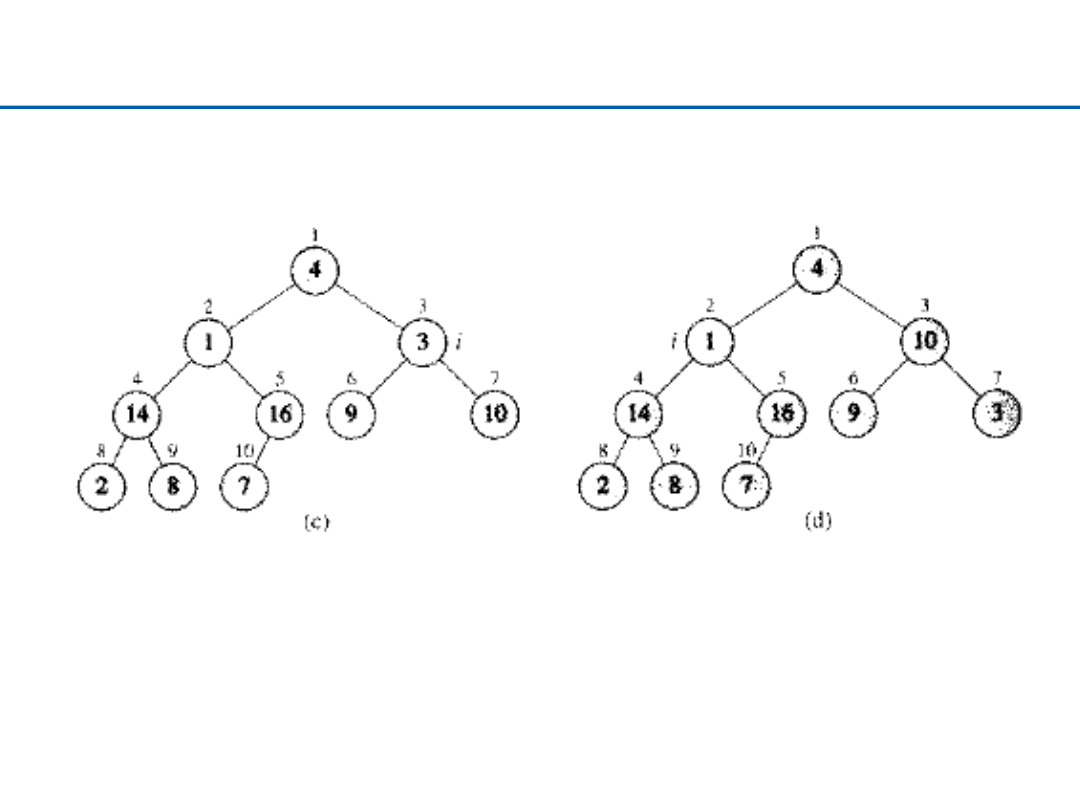
33

Budowanie kopca – 2

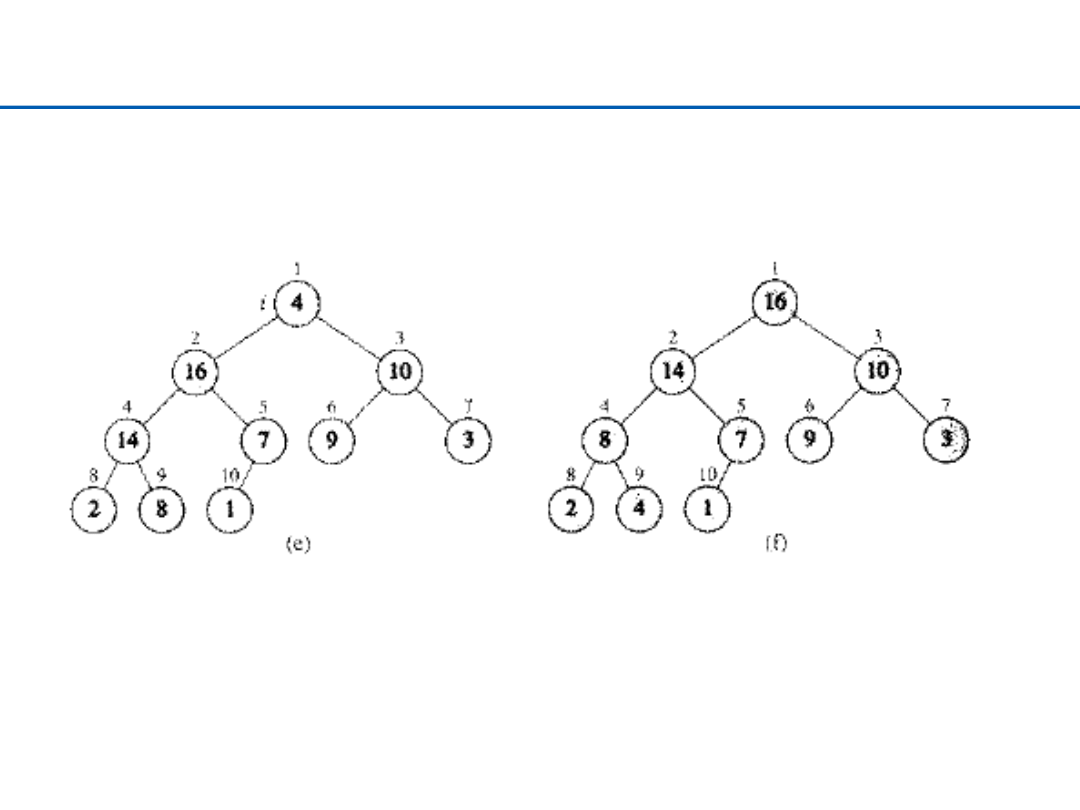
34

Budowanie kopca – 3

35

Budowa kopca – analiza

Ø

 

Poprawność: indukcja po

i

, (wszystkie drzewa o korzeniach

m

>

i

są

kopcami)

Ø

 

Czas działania:

n

wywołań kopcowania (Heapify) =

n O(lg n) = O(n lg n)

Ø

 

Wystarczająco dobre ograniczenie –

O(n lg n)

dla zadania sortowanie

(Heapsort), ale czasem kopiec budujemy dla innych celów

36

Sortowanie za pomocą kopca – Heap Sort

Ø

 

Czas działania

O(n lg n)

+ czas budowy kopca (

O(n))

O( )

n

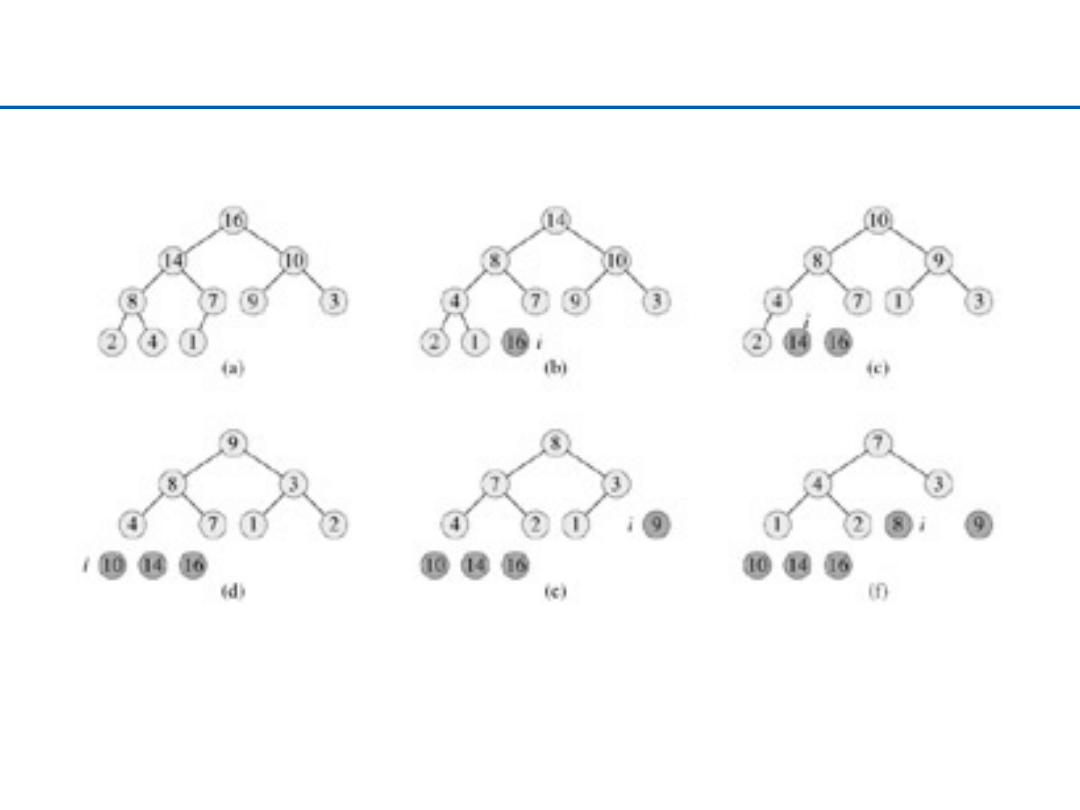
37

Heap Sort – 1

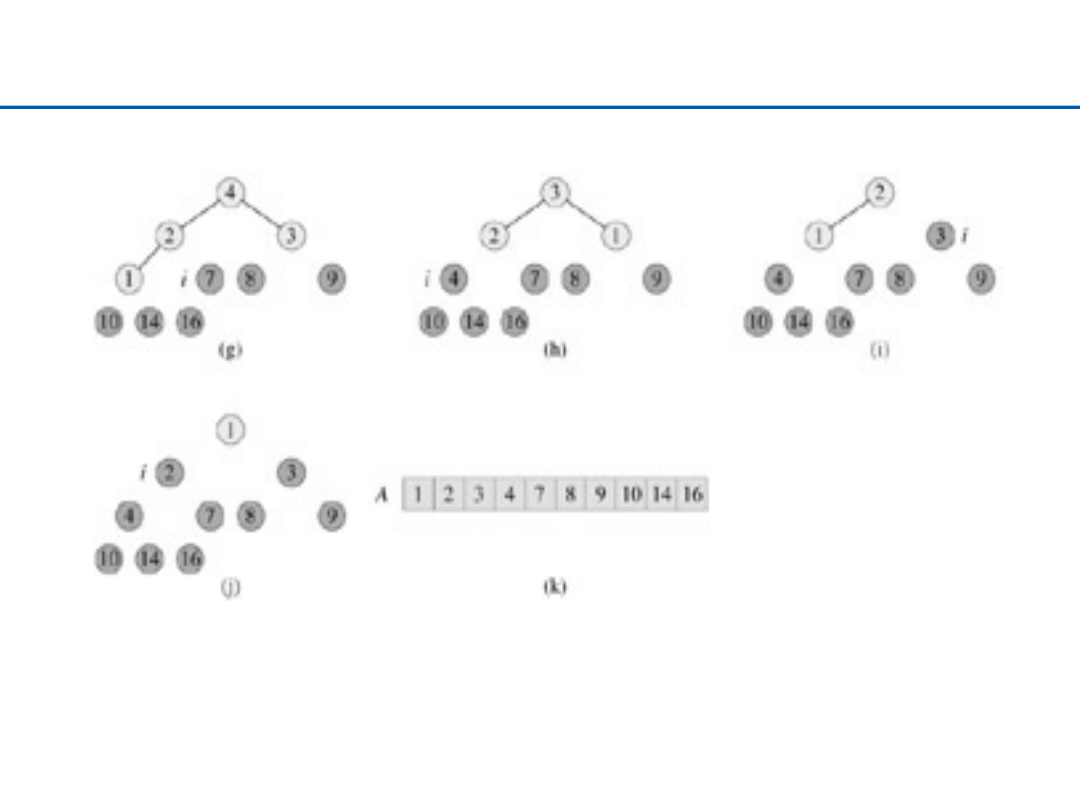
38

Heap Sort – 2

39

Heap Sort – podsumowanie

Ø

 

Heap sort wykorzystuje strukturę kopca przez co dostajemy
asymptotycznie optymalny czas sortowania

Ø

 

Czas działania

O(n log n)

– podobnie do merge sort, i lepiej niż wybór,

wstawianie czy bąbelkowe

Ø

 

Sortowanie w miejscu – podobnie do sortowania przez wybór, wstawianie
czy bąbelkowego