Paweł Grzegrzółka AiR 1

Grzegorz Barnik

Identyfikacja obiektów dynamicznych

1. Układ inercyjny pierwszego rzędu:

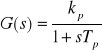
Wartości pomierzone na podstawie odpowiedzi skokowej to:

k_p = 0.75

T­­­­_p­­­ = 0.72 ms

Wartości pomierzone na podstawie charakterystyk częstotliwościowych to:

Optymalne wartości wyznaczone przez MATLABową funkcje fmins:

k_p = 0.7407

T­­­­_p­­­ = 0.7302 ms

Charakterystyki Bodego wraz z modelami optymalnymi:

Charakterystyka Nyquista:

2. Układ inercyjny pierwszego rzędu z opóźnieniem transportowym

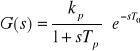
Wartości pomierzone na podstawie odpowiedzi skokowej to:

k_p = 0.72

T­­­­_p­­­ = 0.72 ms

T₀ = 0.2 ms

Wartości pomierzone na podstawie charakterystyk częstotliwościowych to:

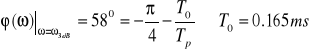
Optymalne wartości wyznaczone przez MATLABową funkcje fmins:

k_p = 0.7132

T­­­­_p­­­ = 0.7065 ms

T₀ = 0.1808 ms

Charakterystyki Bodego wraz z modelami optymalnymi:

Charakterystyka Nyquista:

3. Układ całkujący (mierzonego w zamkniętej pętli sprzężenia zwrotnego)

został on pomierzony w ujemnym sprzężeniu zwrotnym

Wartości pomierzone na podstawie odpowiedzi skokowej to:

k_p = 2.36

T­­­­_p­­­ = 0.4 ms

Wartości pomierzone na podstawie charakterystyk częstotliwościowych to:

Optymalne wartości wyznaczone przez MATLABową funkcje fmins:

k_p = 2.3561

T­­­­_p­­­ = 0.377 ms => T_i = 0.377 ms

Charakterystyki Bodego wraz z modelami optymalnymi:

Charakterystyka Nyquista:

4. Układ drugiego rzędu

Wartości pomierzone na podstawie odpowiedzi skokowej i charakterystyki amplitudowej to:

h_max = 2.76 V

h(
) = 2.44 V

T_k = 1.4 ms

z których to obliczyliśmy w dwóch różnych metodach identyfikacji:

1)
2)

i na ich podstawie ze wzorów umieszczonych w tabeli 1.1:

ζ = 0.8992 ζ = 0.5885

τ =
τ =

więc:

a₁ =
a₁ =

a₂ =
a₂ =

Wartości pomierzone na podstawie charakterystyk częstotliwościowych to:

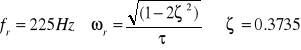
a₁ =

a₂ =

Optymalne wartości wyznaczone przez MATLABową funkcje fmins:

a₁ =

a₂ =

Charakterystyki Bodego wraz z modelami optymalnymi:

Charakterystyka Nyquista:

5. Układ nieminimalnofazowy

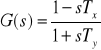
Wartości pomierzone na podstawie odpowiedzi skokowej to:

t₀ = 0.36 ms

x = 3.26

Na podstawie czego obliczyliśmy:

= 0.2484 ms

T_x = x T_y = 0.8098 ms

Wartości pomierzone na podstawie charakterystyk częstotliwościowych to:

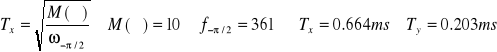
Optymalne wartości wyznaczone przez MATLABową funkcje fmins:

T­­­­_­­x = 0.7731 ms

T_y = 0.2403 ms

Charakterystyki Bodego wraz z modelami optymalnymi:

Charakterystyka Nyquista:

Porównanie różnych metod identyfikacji:

Układ:	Odp skokowa	Odp. częstotliwość	MATLAB
A	kp = 0.75 T­­­­p­­­ = 0.72 ms	kp = 0.79	kp = 0.7407 T­­­­p­­­ = 0.7302ms
	1.2% 1.4%	6.2% 0.8%
B	kp = 0.72 T­­­­p­­­ = 0.72 ms T0 = 0.2 ms	kp = 0.8	kp = 0.7132 T­­­­p­­­ = 0.7065 ms T0 = 0.1808 ms
	0.9% 1.9% 10.6%	12.2% 2.8% 9.6%
C	kp = 2.36 T­­­­p­­­ = 0.4 ms	kp = 2.41 T­­­­p­­­ = 0.394 ms	kp = 2.356 Ti = 0.377 ms
	0.2% 6.1%	2.3% 4.5%
D	a1 = a2 = a2 =	a1 = a2 =	a1 = a2 =
	157% 28.4%	6.2% 153%
E	Tx = 0.8098 ms 0.2484 ms		T­­­­­­x = 0.7731 ms Ty = 0.2403 ms
	4.7% 3.4%	16.4% 18.4%

W tabeli zostały zamieszczone wyniki parametrów poszczególnych układach, wyliczonych różnymi metodami. Oczywiście metoda wykorzystująca matlabową funkcje fmins, która uwzględnia wszystkie punkty pomiarowe, a nie tylko poszczególne charakterystyczne punkty na wykresie, jest metodą najdokładniejszą. I to względem niej zostało przeprowadzone porównanie. Pomijając układ drugiego rzędu metoda bazująca na charakterystyce odpowiedzi skokowej ma średni błąd ok. 3% i tym samym okazuje się dokładniejszą od opierającej się na charakterystykach Bodego, która dokładność jest nieznacznie mniejsza, bo ok. 8%.

1

---