POLITECHNIKA WARSZAWSKA

Laboratorium z przedmiotu: PODSTAWY TECHNIKI POMIAROWEJ Ćwiczenie nr 1. Temat : Ocena błędów wyników pomiarów. STUDIA ZAOCZNE sem. VI Grupa LTK Zespół nr 6 : 1. BYSZKO MIROSŁAW 2. SZKÓŁKA HENRYK 3. KUCHARSKI JERZY 4. ZARZYCKI PIOTR Data wykonania ćwiczenia : 22.02.2002r.

1. CEL ĆWICZENIA

Celem ćwiczenia jest sprawdzenie błędów pomiarowych przyrządów oraz oceny błędów wyników pomiarów.

W teorii błędów, ze względu na przyczyny ich powstawania, możemy dokonać podziału na:

1. Błędy przypadkowe, które wynikają z nieuchwytnych drobnych wpływów i które sprawiają, że żądane wymiary poszczególnych detali lub wyniki pomiarów różnią się między sobą.

2. Błędy systematyczne, które występują przede wszystkim w sposób regularny i wynikają z przyczyn określonych.

3. Błędy grube, które są spowodowane najczęściej awarią, złym zamocowaniem przedmiotu mierzonego lub złym ustawieniem, względnie brakiem kwalifikacji osoby dokonującej pomiar.

Szacowanie błędów pomiarowych odpowiadających rozkładowi normalnemu przy liczbie pomiarów n ≥ 15

Metoda Trzysigmowa

Wynik pomiaru X jest zmienną losową, po wykonaniu n pomiarów tej samej wielkości tą samą metodą otrzymuje się ciąg realizacji zmiennej losowej

Naszym celem jest oszacowanie nie znanej wartości oczekiwanej μ = Ex. Najczęściej tym oszacowaniem jest wartość średnia wyników (wartość średnia z próbki n-elementowej)

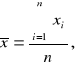
gdzie:

x - jest określane jako estymator wartości oczekiwanej.

Miarą rozproszenia wyników pomiarów dookoła μ jest średnie odchylenie kwadratowe σ.

Dla zbioru {x_i} dyskretnego wyników pomiarów przy założeniu, że n jest duże σ opisuje się:

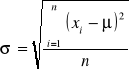
Szacowanie błędów pomiarów odpowiadających rozkładowi normalnemu przy liczbie pomiarów n < 15

Rozkład t Studenta

Nie można przeprowadzić oceny błędu metodą klasyczną (trzysigmową) przy małej ilości pomiarów (mniejszej niż 15), gdyż wyniki tego typu obarczone są dużym błędem.

Przy założeniu, że wyniki pomiarów mają rozkład normalny, można dowieść, że zmienna losowa unormowana

podlega rozkładowi t Studenta T(t, k), gdzie:

k = n - 1 - liczba stopni swobody.

Poza tym T(t, k) nie zależy od nie znanego σ, a tylko od k (k = 1, 2, 3,...,), tak więc n ≥ 2.

2. OPIS STANOWISKA

Do pomiarów zastosowano klasyczne przyrządy służące do sprawdzenia wielkości geometrycznych tj. suwmiarkę i mikrometr.

1. suwmiarka

Rys.1. Noniusz suwmiarki o dokładności 0,05 mm

2. mikrometr

Rys.2. Mikrometr : 1 - wrzeciono, 2 - kabłąk, 3 - kowadełko, 4 - podziałka wzdłużna,

5 - bęben z podziałką obrotową, 6 - sprzęgło, 7 - zacisk

3. PRZEBIEG ĆWICZENIA

Dokonaliśmy 16 - krotnych pomiarów grubości pierścienia metalowego. Pomiary wykonywaliśmy dwukrotnie tj. najpierw dokonaliśmy 16 pomiarów mikrometrem, a następnie dokonaliśmy 16 pomiarów suwmiarką.

Wyniki tych pomiarów zestawiono w poniższej tabeli :

Lp.	Pomiary suwmiarką [mm]	Pomiary mikrometrem [mm]
1	2	3
1	34,80	34,82
2	34,60	34,86
3	34,70	34,79
4	34,80	34,78
5	34,70	34,78
6	34,60	34,95
7	34,75	34,79
8	34,60	34,79
9	34,55	34,86
10	34,75	34,77
11	34,65	34,78
12	34,70	34,76
13	34,80	34,78
14	34,75	34,77
15	34,60	34,76
16	34,65	34,79

Następnie otrzymane wyniki pomiarów wprowadziliśmy do komputera i korzystając z programu LPM1 dokonaliśmy obliczeń.

4. ZESTAWIENIE WYNIKÓW OBLICZEŃ

Przedziały ufności

• suwmiarka

Test trzysigmowy	34,623334 ± 0,347305
Test t Studenta	34,615000 ± 0,349819

• mikrometr

Test trzysigmowy	34,801872 ± 0,027006
Test t Studenta	34,801701 ± 0,021853

Średnie błędy pomiarów

• suwmiarka

Test trzysigmowy	0,115768
Test t Studenta	0,154650

• mikrometr

Test trzysigmowy	0,009002
Test t Studenta	0,009661

5. PRZYKŁADOWE PRZELICZENIE

1. Ocena błędu metodą t - Studenta dla liczby pomiarów mniejszej od 15.

Procedura obliczania granic przedziału obejmującego wartość X :

1. obliczamy wartość n - elementowej próbki ze wzoru :

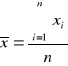
wynik ten przyjmujemy jako oszacowanie poprawnej wartości wielkości mierzonej,

2. obliczamy średnie odchylenie skorygowane s ze wzoru :

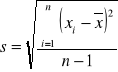
3. dla liczby pomiarów n=10 (czyli k=n-1=9) i poziomu ufności 0,99 (czyli α=0,01) znajdujemy parametr t₁ rozkładu t Studenta ; t₁=3,250

4. obliczamy dodatkowe oszacowanie wartości średniej wg. wzoru :

jest to błąd średni średniej arytmetycznej,

5. wynik pomiaru zapisujemy jako :

2. Metoda trzysigmowa - liczba pomiarów n=16

1. obliczenie wartości średniej wg. wzoru :

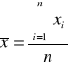
wzór przykładowego obliczenia pokazano w pkt. 1 dla 10 pomiarów

2. obliczamy oszacowanie odchylenia średniego kwadratowego; dla liczby pomiarów n=30 można obliczać
   wg. wzoru :

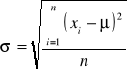
przyjmując

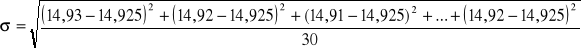
jest to błąd średni pomiaru.

3. obliczamy oszacowanie S odchylenia średniego kwadratowego wartości średniej wg. wzoru :

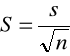
korzystając z założenia, że dla liczby pomiarów

jest to błąd średni średniej arytmetycznej,

4. obliczenie błędu trzysigmowego :

5. wynik pomiaru wynosi :

3,5066<X<3,5623

6. WNIOSKI

Wykonaliśmy pomiar jednego elementu za pomocą mikrometru i suwmiarki. Za pomocą rozkładu normalnego t Studenta i rozkładu trzysigmowego uzyskaliśmy - dzięki programowi komputerowemu LPM1:

• Wartość średnią pomiaru;

• Błąd średni pomiaru;

• Błąd średni średniej arytmetycznej;

• Przedział ufności dla poszczególnych wyników

W wyniku tego ustaliliśmy, że mikrometr jest przyrządem o większej dokładności i pomiary nim dokonane obarczone są mniejszym błędem - dowodem na to są wartości wyników bliskie zeru

• mikrometr 0,009002 i 0,009661

• suwmiarka 0,115768 i 0,154650

Należy dodać, że metoda rozkładu normalnego trzysigmowego jest dokładniejsza od metody t Studenta.

Ponadto ćwiczenie dowiodło, iż im większa ilość pomiarów, tym wynik jest dokładniejszy i bliższy wymiarowi rzeczywistemu. Dowodzi to, że chcąc mieć pomiar odpowiadający rzeczywistości należy wykonać około trzydziestu pomiarów.

Obie metody dowiodły, że dokładność pomiaru zależy od ilości pomiaru tego samego elementu w tym samym miejscu.

1

4

---