Politechnika Śląska 24.luty 2001r.
Wydział Elektryczny
WZG. Sem 6
Rok akad. 2000/2001
Temat ćwiczenia: Regulacja nadążna.
Sekcja 6
Paweł Florian
Arkadiusz Kępa
Grzegorz Wawręty
WPROWADZENIE.
Układy regulacji nadążnej mają podstawową strukturę typową dla wszystkich zamkniętych układów regulacji z głównymi blokami: węzeł sumacyjny , regulator, element wykonawczy, sterowany obiekt oraz układ pomiarowy wielkości wyjściowej w torze ujemnego sprzężenia zwrotnego. Często stosowaną modyfikacją podstawowej struktury, szczególnie w układach mechanicznych, jest wprowadzenie dodatkowego sprzężenia zwrotnego, przez co uzyskuje się tzw. układ regulacji kaskadowej. Rozwiązanie takie pozwala na znaczne polepszenie jakości regulacji, szczególnie w przypadkach, gdy elementy wykonawcze lub obiekt wykazują znaczną nieliniowość, niejednoznaczność (histerezę) lub opóźnienie.
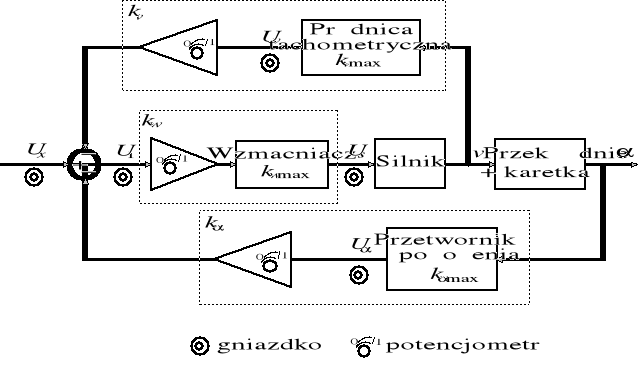
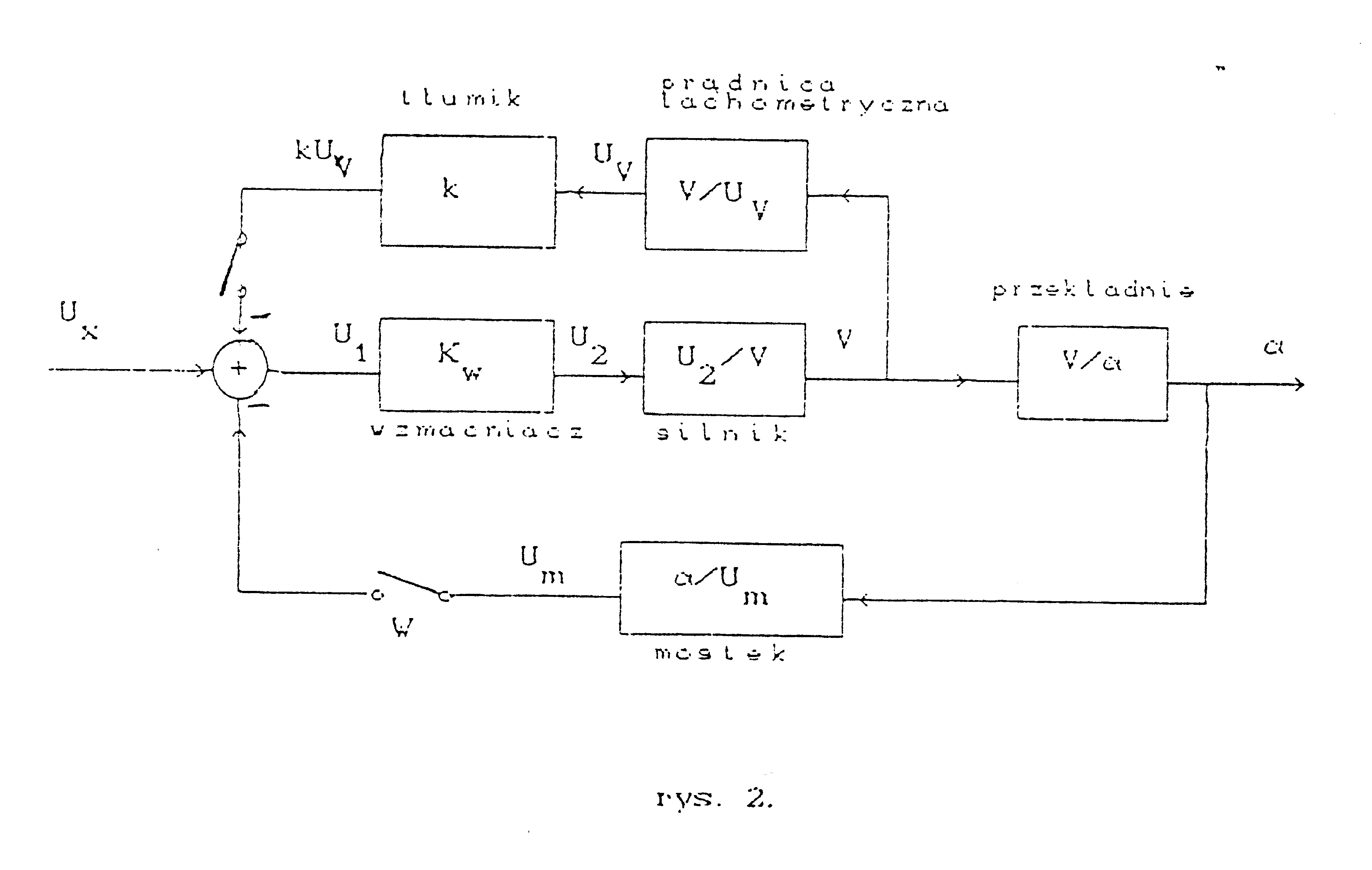
Schemat badanego układu regulacji nadążnej.
MODELE ELEMENTÓW UKŁADU
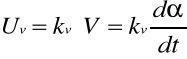
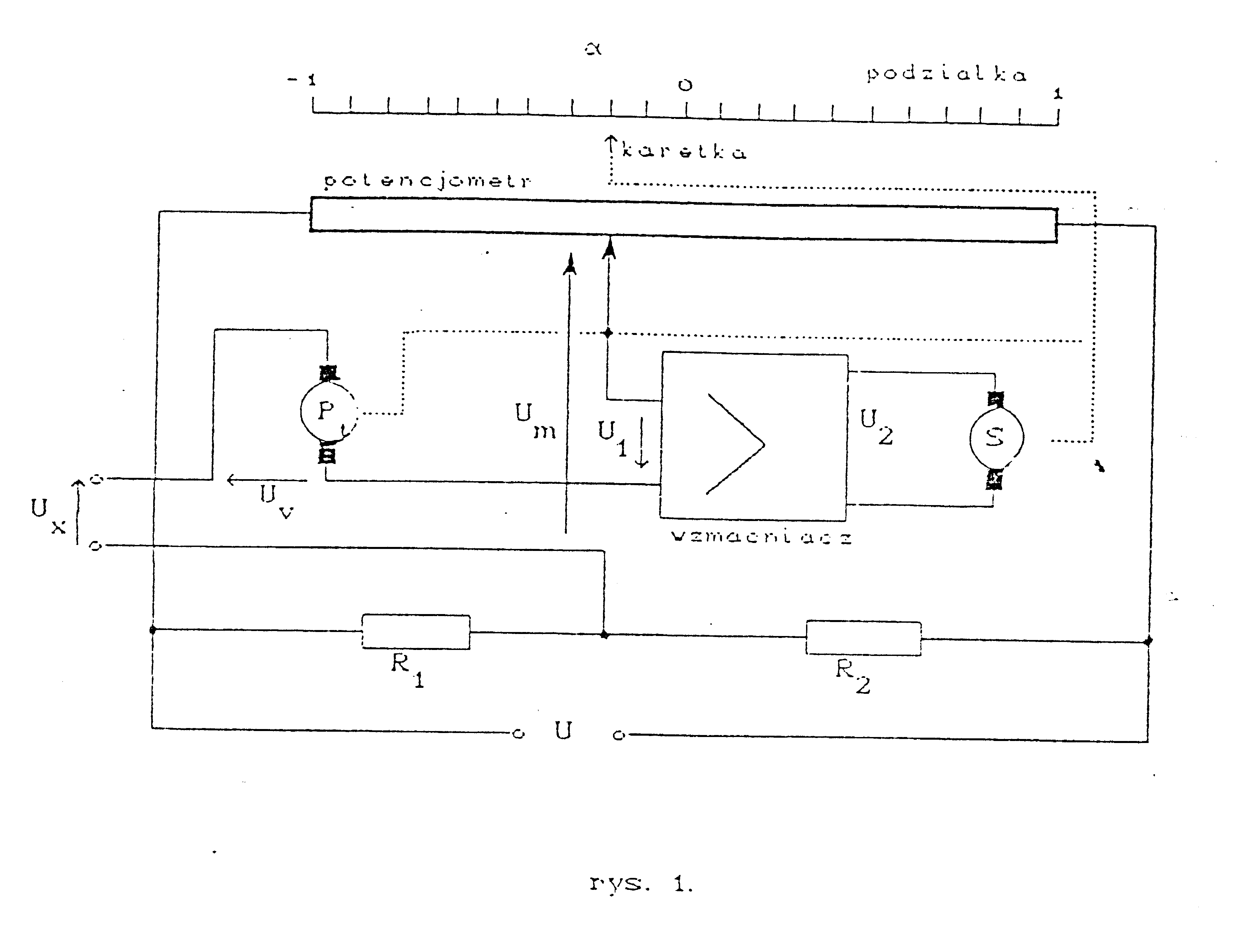
Prędkość ruchu karetki V przetwarzana jest na napięcie Uv za pomocą prądnicy tachometrycznej sprzężonej z karetką przekładniami mechanicznymi. Prądnicę z dobrym przybliżeniem można traktować jak przetwornik śledzący dla prędkości (zerowego rzędu) i opisać modelem w postaci:
Napięcie wyjściowe przetwornika prędkości jest tłumione w układzie tłumika zgodnie z równaniem:
![]()
Położenie karetki przetwarzane jest na napięcie Um za pomocą układu mostkowego z rezystancyjnym przetwornikiem położenia. Układ realizuje zależność:
![]()
![]()
Wzmacniacz sygnału błędu jest elementem zerowego rzędu o równaniu:
Silnik napędzający karetkę poprzez zespół sprzężonych z nim przekładni mechanicznych można traktować jak element inercyjny pierwszego rzędu, ze względu na bezwładność masy wirującej oraz przesuwanej. Można zatem przyjąć model:
![]()
T - stała czasowa silnika; k - współczynnik wzm. statycznego
Przekładnie mechaniczne przenoszą napęd z silnika na przesunięcie karetki. Stała prędkość obrotowa silnika przetworzona jest na stałą prędkość liniową karetki, a to oznacza liniowo zmieniające się położenie karetki. Przekładnie można zatem traktować jak układ całkujący i opisać modelem:
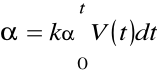
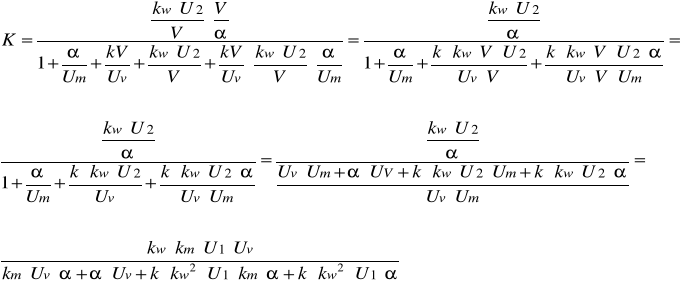
Na podstawie tej struktury, uwzględniając modele poszczególnych elementów, można wyprowadzić transmitancję zastępczą układu. Transmitancja ta ma postać:
5) SCHEMAT IDEOWY I BLOKOWY
WYZNACZENIE PARAMETRÓW UKŁADU.
Wyznaczenie wzmocnienia mostkowego układu pomiaru położenia:
Najpierw odłączyliśmy napięcie wejściowe, aby uzyskać Us=0,
Następnie zmierzyliśmy napięcia U i U na wyjściu układu odpowiadające znanym położeniom karetki 1 i 2 uzyskanym przez ręczne przesuwanie karetki,
Wyznaczyliśmy wzmocnienie wg zależności:
![]()
gdzie: Uα1=4.2 [V] α1=5.5 [cm]
Uα2=6.5 [V] α2=8.5 [cm]
Po wstawieniu danych liczbowych:
![]()
Wyznaczenie wzmocnienia wzmacniacza:
Wyłączyliśmy sprzężenia zwrotne i potencjometr na wejściu wzmacniacza ustawiliśmy w położeniu 1
2) Następnie doprowadziliśmy do wejścia układu napięcie znanej amplitudzie( i zmierzyliśmy odpowiadającą mu amplitudę napięcia wyjściowego
Wzmocnienie kwmax jest to stosunek wartości napięcia wyjściowego do wejściowego.
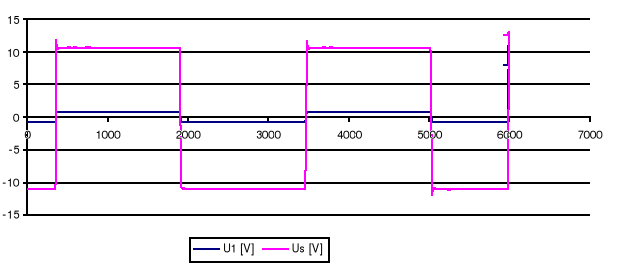
![]()
W ćwiczeniu dokonywaliśmy obserwacji działania układu regulacji dla różnych wartości
współczynników k .
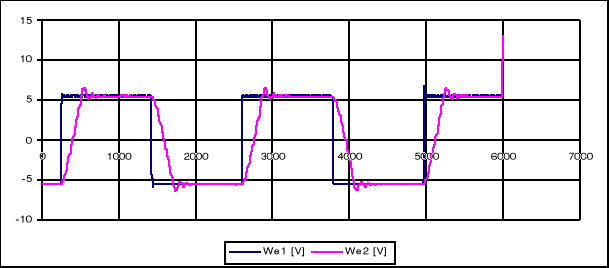
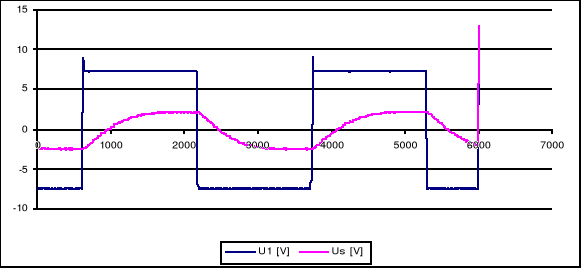
Dla kv=0,6 kw=0,1 km=1
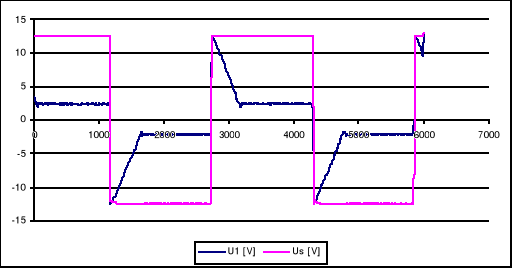
Dla kv=0,5 kw=0,5 km=0,5
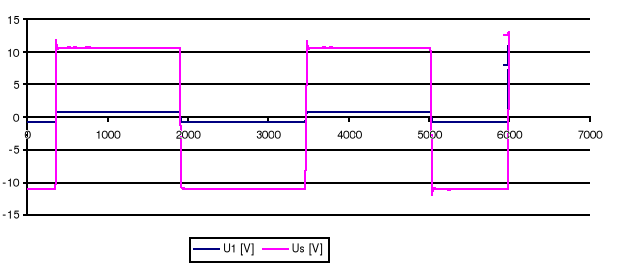
Dla kv=0,6 kw=0,5 km=0
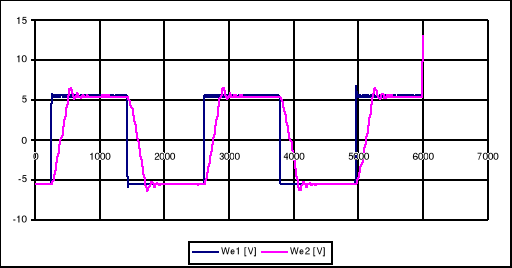
KOMENTARZ DO WYKRESÓW.
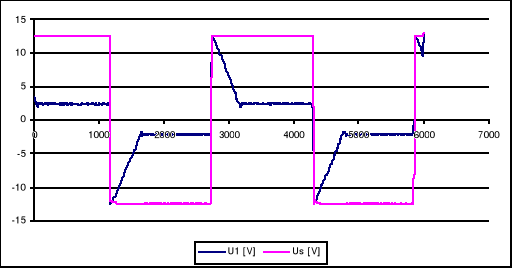
Otwarta pętla sprzężenia zwrotnego od prądnicy tachometrycznej, Km=0,6; K=1; Ux=const; zmiana Km wpływa na amplitudę, jednak nie wpływa na pojawiające się oscylacje.
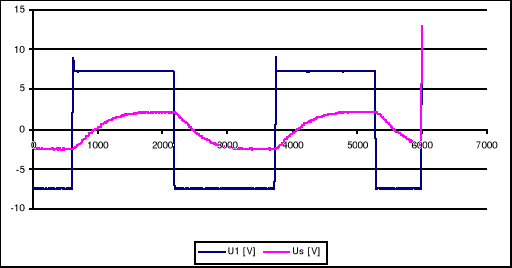
Wyłączone pętle sprzężenia zwrotnego, Kw=0,5 uzyskujemy przebieg trójkątny; zauważamy jego lekkie opadanie, nie pozwala to nam dokładnie ocenić jego amplitudy ( przebieg „nie mieści się” na kartce ), prawdopodobnie w dalszej części ustali się na danym poziomie, jednak nie możemy tego stwierdzić dokładnie.
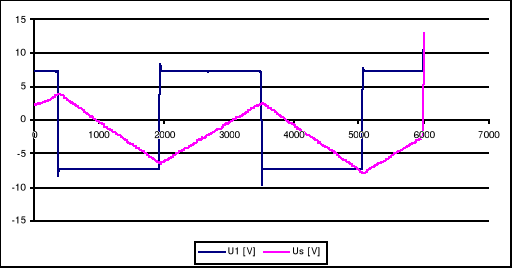
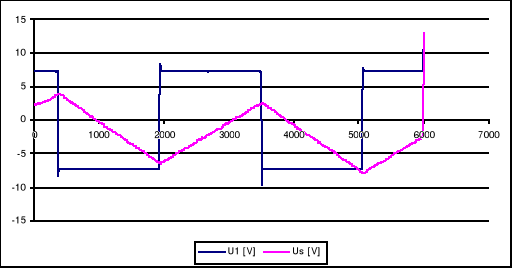
Otwarta pętla sprzężenia zwrotnego z Kv przy Km=0,7 i K=1 powoduje, że przebieg jest prostokątny, jednak maksymalne wartości oscylują, zauwazamy iż zmiana Km ( Km<0,7 ) powoduje powolny zanik oscylacji, aż do uzyskania przebiegu prostokątnego.
Przebieg badany w układzie jak powyżej, przy Km=0,4 przebieg już nie oscyluje ( pojawiają się „małe” delty Diracka w czasie narastania ), zauważamy, że zmniejszenie K powoduje zmniejszenie amplitudy, aż do całkowitego zatrzymania karetki.
Otwarta pętla sprzężenia zwrotnego od prądnicy tachometrycznej, Km=0,6; K=1; Ux=const; zmiana Km wpływa na amplitudę, jednak nie wpływa na pojawiające się oscylacje.
8) WNIOSKI KOŃCOWE
W ćwiczeniu badaliśmy układ regulacji nadążnej czyli wartość zmienna zadana, regulowana jest odwzorowywana jak najdokładniej na wyjściu.
Podczas badań doszliśmy do wniosków ( w większości opisanych w powyższych punktach ), że istotne są wartości wzmocnienia K;Kv;Km, również na „jakość” przebiegu znacząco wpływają poszczególne pętle sprzężenia zwrotnego.
Bardzo ważna jest także stabilność układu, gdyż układ niestabilny nie nadaje się
do zastosowań praktycznych, nie jest w stanie zrealizować celu ( zadania ) sterowania. W ogólności stabilność układu zależy od wszystkich jego parametrów, a więc nie tylko od wzmocnienia.
Układ znajdujący się na granicy stabilności może generować drgania, których amplituda ani się nie zwiększ , ani nie maleje, przekroczenie granicy może powodować generowanie sygnałów o narastającej amplitudzie.
wzm. K>Kkr - układ niestabilny
wzm. K<Kkr - układ stabilny
wzm. K=Kkr - układ na granicy stabilności
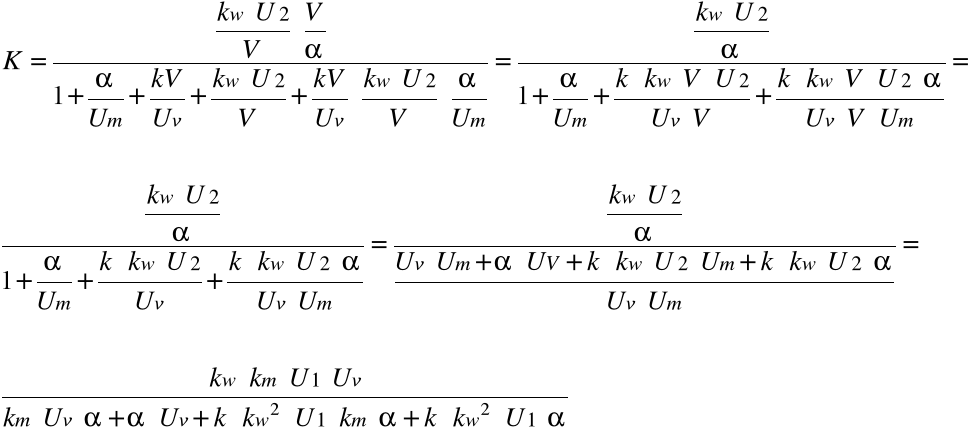
![]()
![]()
![]()
![]()
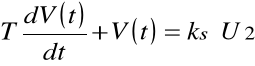
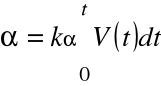
Wyszukiwarka
Podobne podstrony:
KARTA INSTRUKCYJNA OBROBKI2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
17 listopada, Politechnika Śląska semestr I GiG, Górnictwo
wzory Finanase przedsiebiorstw, Politechnika Śląska ZiIP i inne, Finanse
czystakartainstrukcyjnaobrobki, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL,
Rozk ad labów, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Inżynierskie, Se
Politechnika Śląska sprawko moje (Naprawiony)
Politechnika śląska w gliwicach sprawko na dziekana
podstawowe informacje o ochronie prawnej wzorów przemysłowych, Studia - Politechnika Śląska, Zarządz
Projekt (chemia), Uczelnia - Politechnika Slaska, Chemia, Chemia
Testy 5 ekonomika podatkowa, Politechnika Śląska ZiIP i inne, Ekonomika podatkowa
ściąga ciocia, Uczelnia - Politechnika Slaska, Petro Węgla
odp zestaw e, Politechnika Śląska MT MiBM, Semestr III, Bazy danych
ZARZĄDZANIE ŚRODOWISKIEM, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Inżyn
Pstrona MO., POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 2, StudiaI
PKM sciaga, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Inżynierskie, Semes
więcej podobnych podstron