1

Ciągi liczbowe

Definicja

Ciągiem liczbowym nazywamy dowolną funkcję odwzoro-

wującą zbiór liczb naturalnych w zbiór liczb rzeczywistych, tj.

f : N → R

f (n) = a

n

Oznaczenie:

•

a

n - n-ty wyraz ciągu

•

{a

n

}

- ciąg

Sposoby określania ciągu:

•

wzorem:

a

n

= cos(nπ)

•

rekurencyjnie:

a

1

= 1,

a

2

= 3,

a

n+2

= 2a

n

+ a

n+1

2

• opisowo:

a

n - n-ta cyfra po przecinku w rozwinięciu dziesiętnym

liczby

π = 3, 14159265358979323846264338327950288419716939937 . . .

Znane ciągi:

• Ciąg arytmetyczny:

∃

r∈R

∀

n∈N

a

n+1

− a

n

= r

• Ciąg geometryczny:

∃

q∈Rr{0}

∀

n∈N

a

n+1

a

n

= q

3

Definicja

Ciąg

{a

n

}

nazywamy ciągiem ograniczonym, jeżeli

∃

m,M ∈R

∀

n∈N

m 6 a

n

6 M.

Przykład

Zbadaj ograniczoność ciągów

•

a

n

=

1

n+1

+

1

n+2

+ · · · +

1

n+n

•

a

n

= (−2)

n

Definicja

Ciąg

{a

n

}

nazywamy ciągiem

rosnącym

malejącym

nierosnącym

niemalejącym







































































































jeżeli







































































































a

n

< a

n+1

a

n

> a

n+1

a

n

> a

n+1

a

n

6 a

n+1

4

Praktyczne sposoby badania monotoniczności ciągu:

a

n+1

− a

n

a

n+1

a

n

, a

n

> 0 ciąg jest ...

> 0

> 1

rosnący

> 0

> 1

niemalejący

6 0

6 1

nierosnący

< 0

< 1

malejący

Przykład

Zbadaj monotoniczność ciągów

•

a

n

=

1

n+1

+

1

n+2

+ · · · +

1

n+n

•

a

n

=

4

n

(2n)!

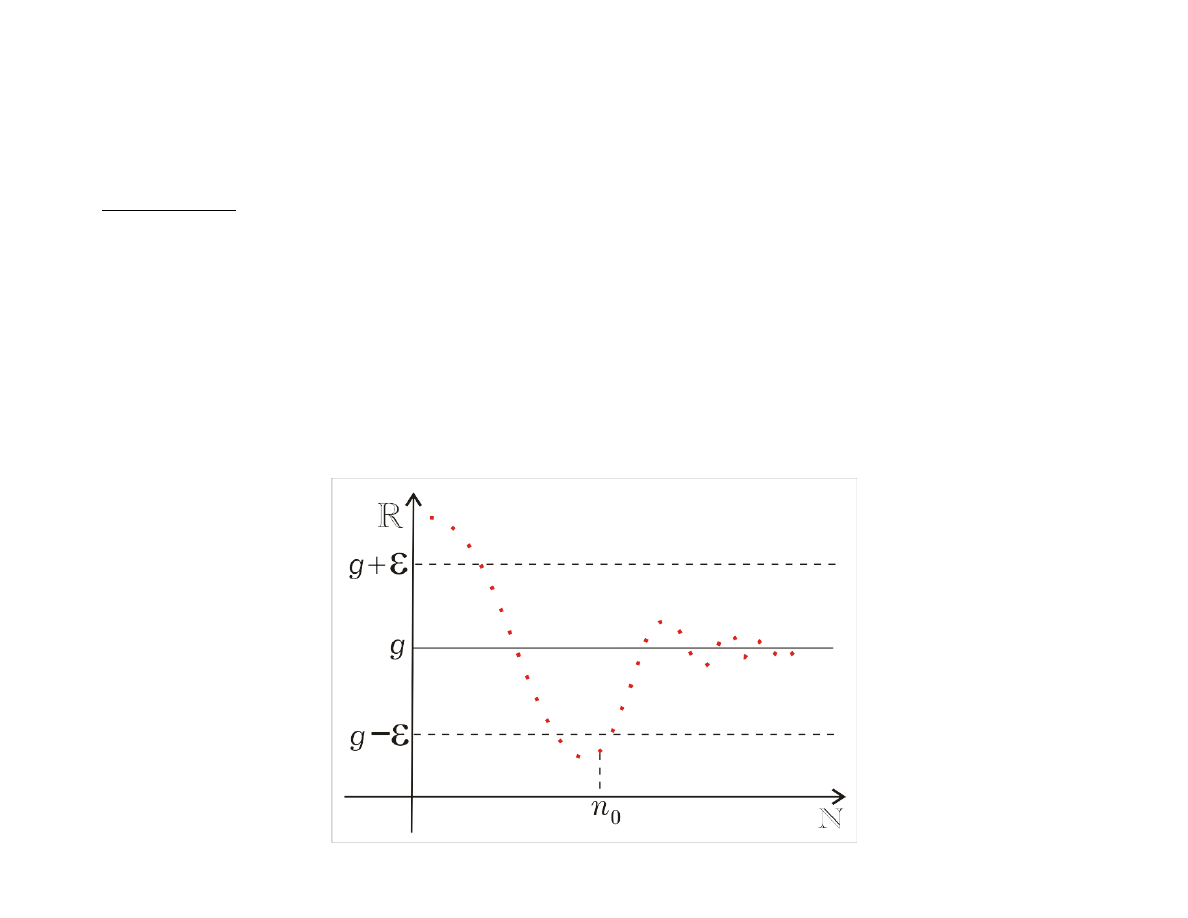
5

Granica ciągu

Definicja

Ciąg

{a

n

}

jest zbieżny do granicy właściwej

g ∈ R

,

co zapisujemy

lim

n→∞

a

n

= g

, wtedy i tylko wtedy, gdy

∀

ε>0

∃

n

0

∈N

∀

n>n

0

| a

n

− g | < ε.

Ciąg, który ma granicę właściwą nazywamy ciągiem zbieżnym.

6

Twierdzenie

Jeżeli ciąg

{a

n

}

jest zbieżny, to posiada on jedną

granicę.

Przykład

Wykaż z definicji, że

lim

n→∞

1

n

= 0

.

Twierdzenie

Jeżeli ciąg

{a

n

}

jest zbieżny, to jest ograniczony.

Uwaga

Twierdzenie odwrotne nie jest prawdziwe, co widać na

przykładzie ciągu

{a

n

}

, dla którego

a

n

= (−1)

n .

Twierdzenie

Jeżeli ciąg

{a

n

}

jest monotoniczny i ograniczony,

to jest zbieżny.

7

Przykład

Rozważmy ciąg

{e

n

}

o wyrazie ogólnym:

e

n

=








1 +

1

n








n

.

Można wykazać, korzystając z nierówności Bernoulliego, że ciąg ten

jest rosnący. Ponadto jest to ciąg ograniczony.

Twierdzenie

Ciąg

{e

n

}

jest zbieżny. Granicę tego ciągu oznacza-

my:

e

, tj.

lim

n→∞








1 +

1

n








n

= e.

8

Arytmetyka granic ciągu

Twierdzenie

Jeżeli ciągi

{a

n

}

i

{b

n

}

są zbieżne, to

•

lim

n→∞

( a

n

± b

n

) =

lim

n→∞

a

n

±

lim

n→∞

b

n

•

lim

n→∞

( c · a

n

) = c · lim

n→∞

a

n ,

gdzie

c ∈ R

•

lim

n→∞

( a

n

· b

n

) =

lim

n→∞

a

n

·

lim

n→∞

b

n

•

lim

n→∞

a

n

b

n

=

lim

n→∞

a

n

lim

n→∞

b

n

,

o ile

lim

n→∞

b

n

6= 0

•

lim

n→∞

( a

n

)

p

=





lim

n→∞

a

n





p

,

gdzie

p ∈ Z r {0}

•

lim

n→∞

k

√

a

n

=

k

s

lim

n→∞

a

n ,

gdzie

k ∈ N r {1}

9

Fakt

• Jeżeli

a > 0

, to

lim

n→∞

n

√

a = 1

.

•

lim

n→∞

n

√

n = 1

Przykład

Oblicz granicę ciągu o wyrazie ogólnym:

a)

a

n

=

n

3

+3n

2

−9n

4n

3

−n+8

b)

a

n

=





2n+3

2n−7





2011

c)

a

n

=

n

4

+n

2

−9·

n

√

n

n

√

2·n

4

−5n

d)

a

n

=

3

v
u
u
u
t

8n

2

+5n−9

n

2

−2n+4

e)

a

n

=

√

n

2

+ 6n + 1 −

√

n

2

+ 3n

10

f )

a

n

=

1+2+...+n

2n

2

+1

g)

a

n

=

1+4+7+...+(3n−2)

n

2

h)

a

n

=

(n+2)!+(n+1)!

(n+3)!

i)

a

n

= 2

n−1

n+3

· arctg

n

4

n

4

+1

11

Ciągi zbieżne do zera

Twierdzenie

lim

n→∞

a

n

=

0

wtedy i tylko wtedy, gdy

lim

n→∞

| a

n

| = 0

.

Twierdzenie

Jeżeli

lim

n→∞

a

n

= 0

oraz ciąg

{b

n

}

jest

ciągiem ograniczonym, to

lim

n→∞

a

n

· b

n

= 0

.

Przykład

Oblicz granicę ciągu o wyrazie ogólnym:

a)

a

n

=

n · (−1)

n

n

2

+1

b)

a

n

=

2n+3

2n

3

−7

· (−1)

n

c)

a

n

=

√

4+(−1)

n

3

√

n+2

d)

a

n

=

1

3

√

n

2

−2n+4

· sin

nπ

3

!

e)

a

n

= (−1)

n





n −

√

n

2

+ 1





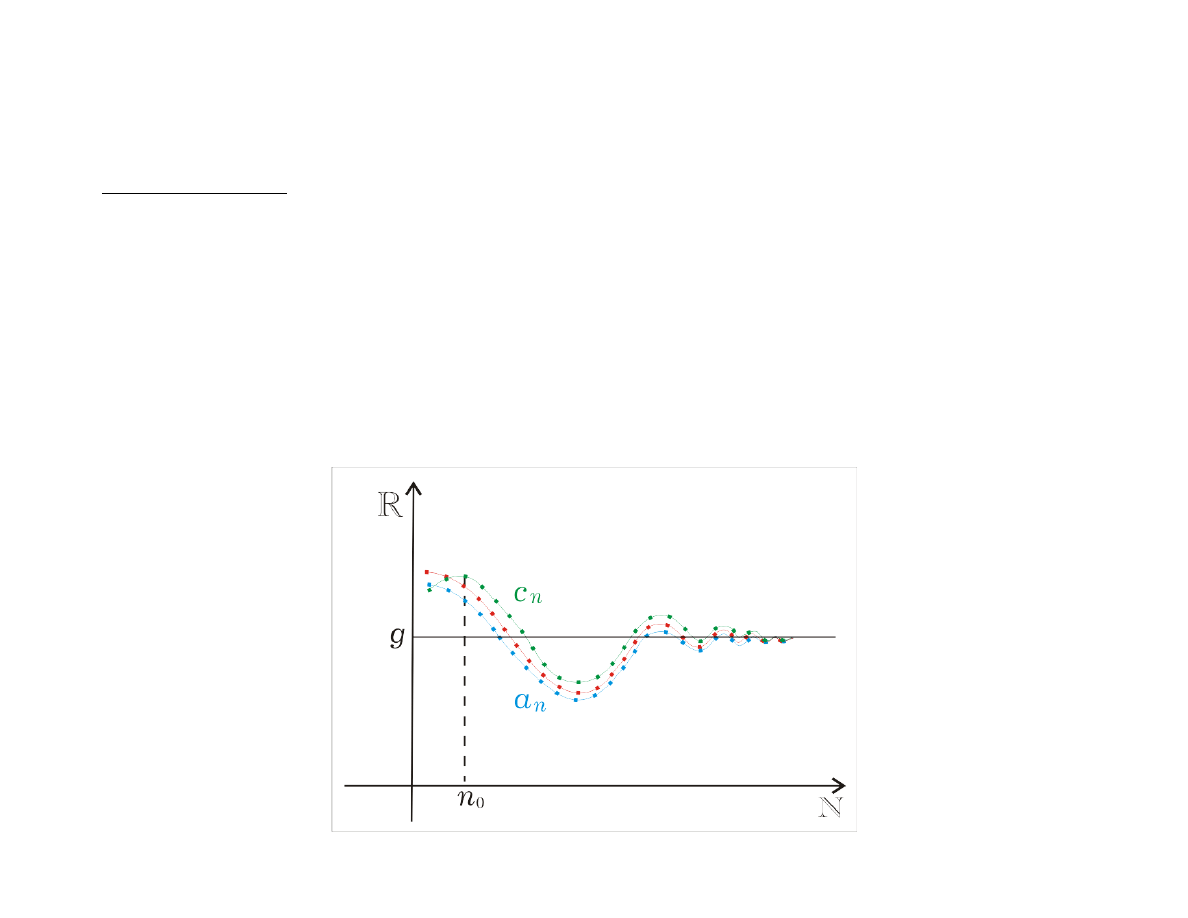
12

Twierdzenie o trzech ciągach

Twierdzenie

Jeżeli ciągi

{a

n

}

,

{b

n

}

i

{c

n

}

spełniają warunki:

•

∃

n

0

∈N

∀

n>n

0

a

n

6 b

n

6 c

n

•

lim

n→∞

a

n

=

lim

n→∞

c

n

= g

,

to ciąg

{b

n

}

jest zbieżny i

lim

n→∞

b

n

= g

.

13

Przykład

Oblicz granicę ciągu o wyrazie ogólnym:

a)

a

n

=

n

√

n

4

+ 64

b)

a

n

=

n

√

e

n

+ 3

n

+ π

n

c)

a

n

=

n

√

n

4

+ 2

n

d)

a

n

=

n! + sin(n!)

n! + 3

e)

a

n

=

1

√

n

2

+1

+

1

√

n

2

+2

+ . . . +

1

√

n

2

+n

Ciągi zbieżne do nieskończoności

Definicja

Ciąg

{a

n

}

jest zbieżny do

+∞

, co zapisujemy

lim

n→∞

a

n

= +∞

, wtedy i tylko wtedy, gdy

∀

M >0

∃

n

0

∈N

∀

n>n

0

a

n

> M.

Ćwiczenie

Napisz definicję ciągu zbieżnego do

−∞

.

14

Definicja

Ciąg, który nie posiada granicy (właściwej lub niewłaściwej)

nazywamy ciągiem rozbieżnym.

Twierdzenie

Jeżeli ciąg

{a

n

}

jest zbieżny do

+∞

lub

−∞

,

to

lim

n→∞








1 +

1

a

n








a

n

= e .

Przykład

Oblicz granicę ciągu o wyrazie ogólnym:

a)

a

n

=





1 −

5

n





2n

b)

a

n

=





2n+3

2n−7





n

c)

a

n

=





1 +

4

n!





n!+1

d)

a

n

=






n

3

−8

n

3

+8






2n

3

+2011

15

Fakt

(granice ciągu geometrycznego)

lim

n→∞

q

n







































































































= 0

dla

|q| < 1

= 1

dla

q = 1

= +∞

dla

q > 1

nie istnieje

dla

q 6 −1

Przykład

Oblicz granicę ciągu o wyrazie ogólnym:

a)

a

n

=

2·3

2n

+ 1

9

n

+ 9

b)

a

n

=

(−2)

n

+ 4·5

n

3·7

n

+ 2

2n

c)

a

n

=

1 +

1
2

+

1

2

2

+ . . . +

1

2

n

1 +

1

e

+

1

e

2

+ . . . +

1

e

n

16

Twierdzenie

(o granicach niewłaściwych ciągów)

•

a + ∞ = ∞

dla

−∞ < a 6 ∞

•

a · ∞ = ∞

dla

0 < a

6 ∞

•

a

∞

= 0

dla

−∞ < a < ∞

•

a

0

+

= ∞

dla

0 < a

6 ∞

Definicja

Następujące symbole nazywamy wyrażeniami nieozna-

czonymi

∞ − ∞,

0 · ∞,

0

0

,

∞
∞

,

1

∞

,

∞

0

,

0

0

.