Przegląd metod całkowania równań różniczkowych
zwyczajnych

Spis treści

[

schowaj

]

•

1 Przegląd metod całkowania równań różniczkowych zwyczajnych

•

2 Równanie różniczkowe o zmiennych rozdzielonych

•

3 Równanie różniczkowe jednorodne

•

4 Równanie różniczkowe liniowe rzędu pierwszego

•

5 Równanie Bernoullego

•

6 Równanie różniczkowe zupełne

•

7 Równanie różniczkowe liniowe rzędu o stałych współczynnikach

Przegląd metod całkowania równań różniczkowych zwyczajnych

Ten wykład prezentuje metody rozwiązywania wybranych typów równań różniczkowych. Pokazujemy,
jak otrzymać rozwiązanie ogólne dla równań rzędu pierwszego: równania o zmiennych rozdzielonych,
równania jednorodnego, równania liniowego, równania Bernoullego i równania różniczkowego
zupełnego. Z równań wyższych rzędów zajmujemy się tylko równaniem liniowym (jednorodnym i
niejednorodnym) o stałych współczynnikach.

Uwaga 14.1.

Przez rozwiązanie równania rozumiemy w tym wykładzie zarówno podanie rozwiązania w postaci
jawnej, to znaczy podanie wzoru na szukaną funkcję

jak też podanie rozwiązania w postaci

uwikłanej, czyli

gdzie jest stałą dowolną. Aby zapewnić istnienie i jednoznaczność

rozwiązań, zakładamy, że wszystkie występujące w naszym wykładzie funkcje są klasy

w pewnym

przedziale

, względnie w kostce

Na wykładzie pokazujemy tylko, jak

dostać rozwiązanie ogólne równania, przykłady rozwiązań problemów Cauchy'ego zostawiamy na
ćwiczenia.

Równanie różniczkowe o zmiennych rozdzielonych

D

EFINICJA

14.2.

Równanie różniczkowe

czyli

lub równoważnie

nazywamy równaniem różniczkowym o zmiennych rozdzielonych (rrzr).

Równanie to rozwiązujemy, "rozdzielając zmienne", czyli grupując wyrażenia z po jednej stronie, a
wyrażenia z po drugiej stronie znaku równości. Otrzymujemy:

skąd rozwiązanie ogólne równania (rrzr) dostajemy w postaci

gdzie przez zapis

i

rozumiemy dowolną pierwotną z funkcji podcałkowej i gdzie

jest stałą dowolną.

Uwaga 14.3.

Postępując jak powyżej, mogliśmy "zgubić" pewne rozwiązania równania (rrzr). Dokładniej, skoro
dzielimy (rrzr) przez

stronami, to nasze rozwiązanie nie uwzględnia rozwiązań postaci

gdzie jest takie, że

Te rozwiązania (o ile istnieją) musimy dołączyć do rozwiązania

ogólnego równania (rrzr).

Z problemem "gubienia" pewnych rozwiązań spotkamy się na tym wykładzie jeszcze niejednokrotnie.
Dla zaznaczenia, że musimy osobno rozważać pewne rozwiązania, będziemy pisać obok równania na
przykład:

zaznaczając w ten sposób, że należy rozważyć, czy rozwiązania postaci

dla

są

rozwiązaniami naszego równania.

A zatem rozwiązania (rrzr) są postaci

lub

dla

P

RZYKŁAD

14.4.

Rozwiązać równanie

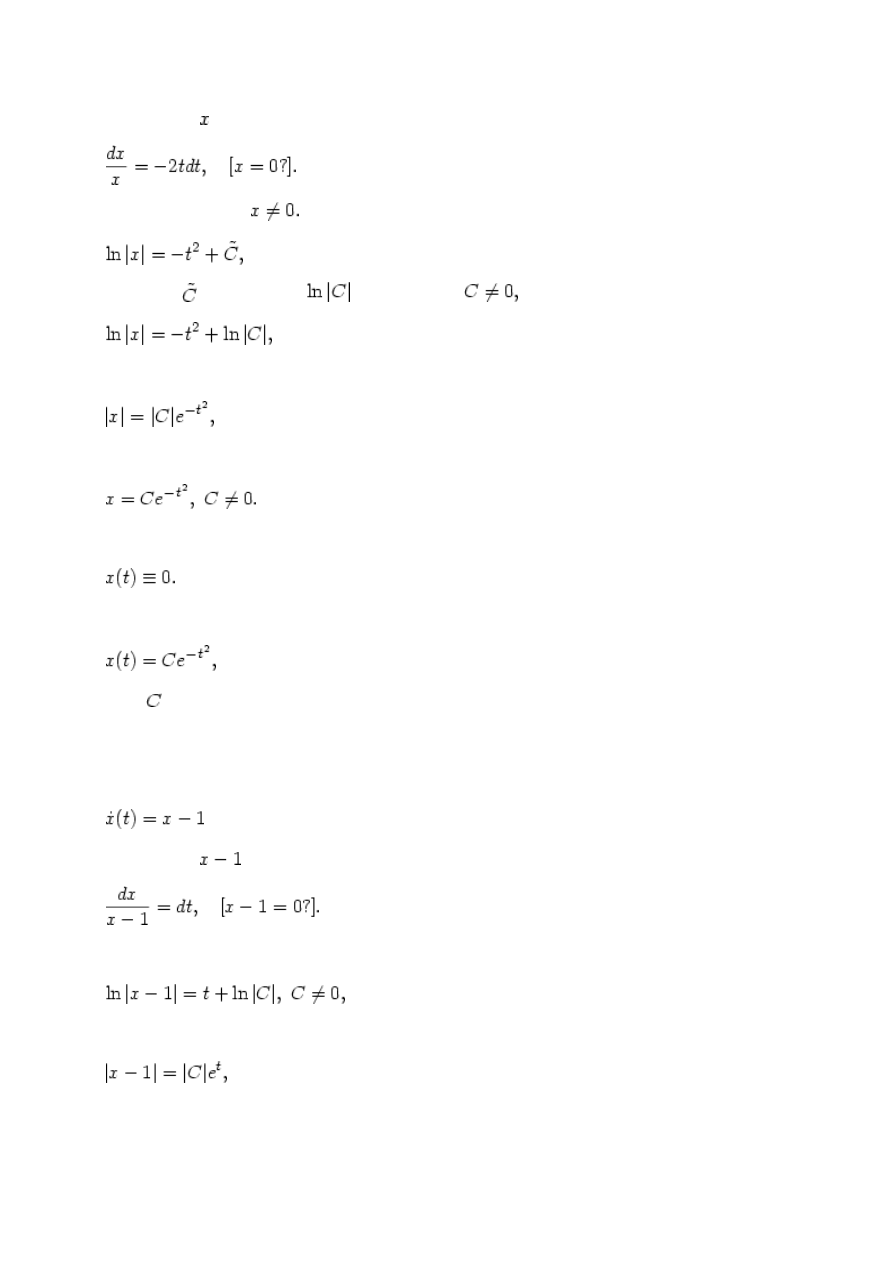
Dzieląc przez , dostajemy

Odtąd zakładamy, że

Całkując, mamy

gdzie stałą zapisujemy jako

dla pewnej stałej

a zatem

czyli

a więc

Oprócz tego, jak od razu widać, rozwiązaniem jest funkcja

Reasumując, możemy napisać, że wszystkie rozwiązania naszego równania są postaci

gdzie jest stałą dowolną.

P

RZYKŁAD

14.5.

Rozwiązać równanie

Dzieląc przez

, dostajemy

Całkując, mamy

czyli

a więc

Dodatkowo

także jest rozwiązaniem naszego równania.

A zatem wszystkie rozwiązania naszego równania są postaci

gdzie jest stałą dowolną.

Równanie różniczkowe jednorodne

D

EFINICJA

14.6.

Funkcja

jest funkcją jednorodną stopnia (gdzie

), jeśli dla każdego

i

wszystkich

z dziedziny funkcji,

też należy do dziedziny oraz zachodzi

P

RZYKŁAD

14.7.

(1) Funkcja

jest funkcją jednorodną stopnia

(2) Funkcja

jest funkcją jednorodną stopnia

(3) Funkcja

nie jest funkcją jednorodną.

D

EFINICJA

14.8.

Równanie różniczkowe

gdzie i są funkcjami jednorodnymi tego samego stopnia , nazywamy równaniem
różniczkowym jednorodnym (rrj).

Uwaga 14.9.

Równanie różniczkowe jednorodne możemy zawsze sprowadzić do postaci (rrj'):

Faktycznie, dzieląc (rrj) przez

, a następnie dzieląc licznik i mianownik

przez

,

dostajemy postać (rrj').

Równanie (rrj') rozwiązujemy, podstawiając

Mamy zatem

a więc podstawiając do (rrj'), dostajemy równanie

różniczkowe o zmiennych rozdzielonych

To równanie rozwiązujemy znaną już metodą i dostajemy:

P

RZYKŁAD

14.10.

Rozwiązać równanie

To jest równanie jednorodne. (Funkcje są jednorodne stopnia ). Dzielimy stronami przez i
dostajemy:

Podstawiając

, otrzymujemy równanie:

zatem

Rozwiązaniem tego równania jest

gdzie jest dowolną stałą. Skoro

, to

Równanie różniczkowe liniowe rzędu pierwszego

D

EFINICJA

14.11.

Równanie różniczkowe

nazywamy równaniem różniczkowym liniowym rzędu pierwszego (rrl-1).

Jeśli funkcja

, to równanie

nazywamy równaniem różniczkowym liniowym jednorodnym rzędu pierwszego (rrlj-1).

Jeśli funkcja

nie jest tożsamościowo równa zero, to równanie

nazywamy równaniem różniczkowym liniowym niejednorodnym rzędu pierwszego (rrlnj-1).

Najpierw pokażemy, jak znaleźć rozwiązania równania różniczkowego liniowego jednorodnego (rrlj-1)

Widać, że jest to równanie o zmiennych rozdzielonych,

czyli

Całkując, dostajemy:

gdzie jest stałą dowolną. (Uwzględniliśmy już, że

jest rozwiązaniem naszego równania

(rrlj-1)).

Przypuśćmy teraz, że mamy rozwiązać równanie różniczkowe liniowe rzędu pierwszego,
niejednorodne,

Zachodzi następujące stwierdzenie (dowód pomijamy).

S

TWIERDZENIE

14.12.

Rozwiązanie ogólne równania różniczkowego liniowego niejednorodnego rzędu pierwszego jest sumą
rozwiązania ogólnego odpowiadającego równania różniczkowego jednorodnego i szczególnego
rozwiązania równania (rrlnj-1).

A zatem rozwiązujemy równanie (rrlnj-1), znajdując najpierw rozwiązanie odpowiadającego mu
równania różniczkowego liniowego jednorodnego,

czyli funkcję

Następnie musimy znaleźć rozwiązanie ogólne równania niejednorodnego. Zgodnie ze

stwierdzeniem

14.12

, wystarczy znaleźć szczególne rozwiązanie (rrlnj-1). Może nam się udać takie rozwiązanie

szczególne zgadnąć (patrz

przykład 14.15.

) i wtedy wystarczy je dodać do rozwiązania ogólnego

równania jednorodnego. Istnieją także metody szukania rozwiązań szczególnych, tu poznamy jedną z
nich. Jest to tak zwana metoda uzmienniania stałej. Aby zastosować tę metodę, załóżmy, że
rozwiązanie ogólne (rrlnj-1) można zapisać w postaci

gdzie

jest pewną funkcją klasy

którą musimy znaleźć. By wyznaczyć

, podstawmy nasze

do równania

Dostaniemy:

czyli po uproszczeniu

Stąd

czyli

gdzie, jak wcześniej,

oznacza dowolną pierwotną z funkcji podcałkowej, a jest

stałą.

Podstawiając otrzymane

do wzoru na rozwiązanie, dostajemy:

czyli, zapisując zgodnie ze

stwierdzeniem 14.12

, dostajemy następujące stwierdzenie.

S

TWIERDZENIE

14.13.

jest rozwiązaniem ogólnym (rrlnj-1).

Łatwo sprawdzić, że

jest szczególnym rozwiązaniem (rrlnj-1).

P

RZYKŁAD

14.14.

Rozwiązać równanie liniowe niejednorodne:

Zgodnie z wyżej wprowadzonymi oznaczeniami mamy tu

oraz

Rozwiązując

równanie jednorodne, dostajemy

Stosując metodę uzmienniania stałej (lub od razu wstawiając do wzoru na rozwiązanie ogólne), mamy:

jest rozwiązaniem ogólnym naszego równania niejednorodnego.

P

RZYKŁAD

14.15.

Znaleźć rozwiązanie równania

Równanie jednorodne

ma rozwiązanie ogólne

Rozwiązanie szczególne naszego równania niejednorodnego

łatwo zgadnąć, otóż jest to

Tak więc rozwiązanie ogólne równania

, to

zgodnie ze

stwierdzeniem 14.12

,

Równanie Bernoullego

Jakob Bernoulli (1654-1705)

Zobacz biografię

D

EFINICJA

14.16.

Równanie różniczkowe

gdzie

nazywamy równaniem różniczkowym Bernoullego

(rrB).

Zauważmy, że dla

lub

powyższe równanie staje się równaniem różniczkowym liniowym

(jednorodnym lub nie).

ernoullego rozwiązujemy za pomocą podstawienia

Równanie różniczkowe B

, to

i sprowadzenia równania do równania liniowego. Faktycznie, skoro
Mnożąc (rrB) obustronnie przez

, dostajemy równanie

i podstawiając, mamy:

czyli równanie liniowe rzędu pierwszego z niewiadomą funkcją Takie równanie umiemy już
rozwiązać.

ż, że jeśli

Zauważmy te

, czyli

, to zawsze "gubimy" rozwiązanie

.

ie

P

RZYKŁAD

14.17.

Rozwiązać równan

Zapiszmy to równanie jako

Zatem

Nasze równanie, po pomnożeniu obustronnie przez

, zamienia się w równanie

czyli po podstaw

iu

ien

dostajemy równan liniowe niejednorodne

ie

Zgodnie ze

ązanie ogólne równania liniowego podanym w

stwierdzeniem 14.13

mamy

wzorem na rozwi

czyli

a zatem rozwiązanie naszego równania Bernoullego to

Równanie różniczkowe zupełne

dane dwie funkcje

D

EFINICJA

14.18.

Załóżmy, że mamy

klasy

gdzie jest obszarem

jednospójnym w

Równanie różniczkowe

nazywamy równaniem różniczkowym zupełnym (rrz), jeśli w zachodzi

Często definiuje się też równanie różniczkowe zupełne jako takie równanie, że pole wektorowe

jest polem potencjalnym. Jak wiemy, w obszarach jednospójnych te

a, jak metoda szukania

potencjału dla pola potencjalnego (patrz

ćwiczenie 12.4.

). Aby rozwiązać (rrz), wystarczy znaleźć taką

warunki są równoważne (patrz

uwaga 12.17.

oraz

stwierdzeniem 12.19.

).

Metoda rozwiązywania równań różniczkowych zupełnych jest dokładnie tak

funkcję

, by

i

Jeśli znajdziemy takie

, to rozwiązaniem ogólnym (rrz) będzie

ze stałą dowo ą

ln

(Dowód powyższego faktu pomijamy, wymaga bowiem wprowadzenia pojęcia różniczki zupełnej).

Aby znaleźć

całkujemy funkcję

po zmiennej Dostajemy wtedy

gdzie jest pewną, na razie niezna

, funkcją klasy

ną

Aby wyznaczyć , liczymy pochodną po z

obu stron powyższego równania. Dostajemy:

Porównując te strony tego równania, wyznaczamy

a całkując, dostajemy

a zatem także

P

RZYKŁAD

14.19.

ie różniczkowe

Rozwiązać równan

Mamy

Zachodzi

a więc równanie jest zupełne. Wyznaczmy

Mamy

i porówn ąc z

uj

Licząc pochodną po

, dostaniemy:

skąd

a więc

czyli

Równanie różniczkowe liniowe rzędu o stałych współczynnikach

y

erwszego.

Zajmiemy się teraz pewnym szczególnym przypadkiem równań wyższego rzędu, czyli równaniami
liniowymi rzędu

Wszystkie rozpatrywane do tej pory równania był równaniami różniczkowymi rzędu pi

o stałych współczynnikach, dla których to równań możemy opisać metodę

prowadzącą do znalezienia rozwiązań. Należy bowiem zdawać sobie sprawę, że nie ma metod
umożliwiających dokładne rozwiązanie dowolnego równania różniczkowego. W praktyce często
zadowalamy się ozwiązaniami przybliżonymi. Szukaniem rozwiązań przybliżonych zajmuje si
matematyki zwany metodami numerycznymi.

D

EFINICJA

14.20.

r

ę dział

Równanie różniczkowe

gdzie

s

liniowym jednorodnym, r

ą ustalonymi liczbami rzeczywistymi nazywamy równaniem różniczkowym

zędu o stałych wspó zynnikach (rrlj-n).

Równanie różniczkowe

łc

ą ustalonymi liczbami rzeczywistymi, a funkcja

gdzie

s

nie jest tożsamościowo równa

zero, nazywamy równaniem różniczkowym liniowym niejednorodnym, rzędu o stałych
współczynnikach (rrlnj-n).

dowodu).

Rozwiązanie ogólne równania różniczkowego liniowego jednorodnego rzędu

Aby znaleźć rozwiązanie równania liniowego jednorodnego (rrlj-n), oprzemy się na poniższym
stwierdzeniu (podamy go bez

S

TWIERDZENIE

14.21.

o stałych

ombinacja liniową

współczynnikach jest k

rozwiązań szczególnych tego równania ze stałymi dowolnymi

Musimy zatem mieć liniowo niezależnych rozwiązań równania (rrlj-n), gdzie przez liniową
n

jest równa kombinacji liniowej

pozostałych. Aby znaleźć te rozwiązania, przypuśćmy, że funkcja

iezależność funkcji rozumiemy fakt, że żadna z tych funkcji nie

jest szczególnym rozwiązaniem naszego równania. Wstawiając tę funkcję do równania, dostajemy:

czyli

D

EFINICJA

14.22.

Równanie

nazywamy równaniem charakterystycznym dla równania (rrlj-n).

Aby znaleźć rozwiązania szczególne

równania różniczkowego (rrlj-n), musimy najpierw

rozwiązać równanie charakterystyczne dla tego równania. Rozwiązując, należy znaleźć wszystkie
pierwiastków tego równania

(mogą być zespolone!). To jak wyglądają rozwiązania

, zależy od postaci

czyli od tego czy są rzeczywiste, czy zespolone, czy

pojedyncze, czy wielokrotne.

I. Wszystkie pierwia

ia charakterystycznego są różne.

Przypadek I.A.

Przypadek

stki równan

są liczbami rzeczywistymi. Wówczas mamy rozwiązanie szczególne

i rozwiązanie ogólne naszego (rrlj-n) ma postać

liczby zespolone. Przyjmijmy, że

Przypadek I.B. Wśród

są

Zauważmy, że skoro

jest pierwiastkiem równania charakterystycznego, to jest nim także

(bo

są rzecz

naszego równania pierwiastków zesp

parzysta ilość). Niech

ywiste; dla

olonych jest zatem zawsze

Wówczas dostajemy dwa liniowo niezależne rozwiązania

ólne

szczeg

postaci

Niech zatem

będą pierwiastkami zespolonymi, a

rzeczywistymi (może nie być żadnego). Wtedy rozwiązanie ogólne naszego (rrlj-n) ma

postać

Przypadek II. Wśród pierwiastków równania charakterystycznego są pierwiastki wielokrotne.
Przypadek II.A Niech pierwiastek będzie -krotnym rzeczywistym pierwiastkiem równania
charakterystycznego. Odpowiada mu wtedy liniowo niezależnych rozwiązań szczególnych:

Przypadek II.B Niech pierwiastek

będzie -krotnym pierwiastkiem zespolonym równania

harakterystycznego. Wtedy

c

także jest -krotnym pierwiastkiem równania

charakterystycznego i odpowiada im

liniowo niezależnych rozwiązań szczególnych:

rozwiązań

Zauważmy, że za każdym razem dostajemy w sumie

- bo suma ilości

wszystkich pierwiastków równania stopnia liczonych wraz z krotnościami wynosi Rozwiązanie
ogólne (rrlj-n) znajdujemy zatem, biorąc kombinację liniową

P

RZYKŁAD

14.23.

Rozwiązać równanie:

Wypisujemy równanie charakterystyczne:

Równanie to ma dwa różne rozwiązania rzeczywiste

Rozwiązania szczególne to

zatem rozwiązanie ogólne to

P

RZYKŁAD

14.24.

Rozwiązać równanie:

Wypisujemy równanie charakterystyczne:

Równanie to ma jeden pierwiastek podwójny (

)

Zatem rozwiązania szczególne to

a rozwiązanie ogólne to

P

RZYKŁAD

14.25.

Rozwiązać równanie:

Wypisujemy równanie charakterystyczne:

Równanie to ma (dwa sprzężone) pierwiastki zespolone

tak więc tu

Zatem rozwiązania szczególne to

a rozwiązanie ogólne to

Powiemy teraz, jak znaleźć rozwiązania niektórych równań różniczkowych liniowych niejednorodnych
rzędu (rrlnj-m). Ograniczymy się do tych sytuacji, kiedy można zastosować tak zwaną metodę
przewi

ń.

4.26.

ednorodnego rzędu

dywa

Bez dowodu podamy następujące stwierdzenie:

S

TWIERDZENIE

1

Rozwiązanie ogólne równania różniczkowego niej

o stałych współczynnikach:

jest sumą rozwiązania ogólnego równania jednorodnego

i rozwiązania szczególnego równania niejednorodnego.

To właśnie do znalezienia tego szczególnego rozw zania będziemy stosować metodę przewidywań.
Okazuje się, że dla pewnych funkcji

ią

można przewidzieć postać rozwiązania szczególnego.

Przypadek 1. Funkcja

gdzie

jest wielomianem zmiennej oraz liczba nie jest pierwiastkiem równania

charakterystycznego.

Wtedy rozwiązanie szczególne jest postaci

gdzie (którego współczynniki musimy wyznaczyć) jest wielomianem tego samego stopnia co
Przypadek 2. Funkcja

gdzie

jest wielomianem zmiennej oraz liczba jest pierwiastkiem -krotnym równania

charakterystycznego.

Wtedy rozwiązani szczególne jest postaci

e

gdzie jest wielomianem tego samego stopnia co
Przypadek 3. Funkcja

gdzie

i

są wielomianami zmiennej oraz liczba

nie jest pierwiastkiem równania

Wtedy rozwiązanie szczególne jest posta

charakterystycznego.

ci

gdzie

i

są wielomianami stopnia równego

Przypadek 4. Funkcja

gdzie

i

są wielomianami zmiennej oraz liczba

jest pierwiastkiem -krotnym

znego.

Wtedy rozwiązanie szczególne jest posta

równania charakterystyc

ci

gdzie znowu

i

są wielomianami stopnia równego

W każdym z powyższych przypadków współczynniki nieznanych wielomianów wyliczymy, wstawiając

do naszego równania niejednorodnego.

Uwaga 14.27.

W przypadku, gdy funkcja

w równaniu niejednorodnym jest sumą funkcji opisanych w

adkach

przyp

powiedzmy

to szukamy najpierw rozwiązań

szczególnych dla równań niejednorodnych z prawymi stronami równymi

Znajdujemy

funkcji

Szukane rozwiązanie szczególne to

co wynika z liniowości naszego równania.

P

RZYKŁAD

14.28.

Rozwiązać równanie

Rozwiązujemy najpierw równanie jednorodne

Równanie charakterystyc e to

zn

z rozwiązaniami

Tak więc rozwiązanie ogólne równania jednorodnego to

Szukamy tera

związań szczególnych, najpierw dla równania

z ro

Tu

zatem

nie jest pierwiastkiem równania charakterystycznego.

Przewidujemy zatem rozwiązanie szczególne w postaci:

To

wstawiamy do równania

Dostajemy:

skąd dostajemy układ równań

czyli

Tak więc

Rozwiążemy teraz równanie

jest (jednokrotnym) pierwiastkiem równania charakterystycznego. Wielomian

Tu

i liczba

ma stopień Rozwiązania szczególnego szukamy zatem w postaci

do równania

Współczynniki i wyznaczymy, wstawiając

Dostaniemy

skąd

zatem

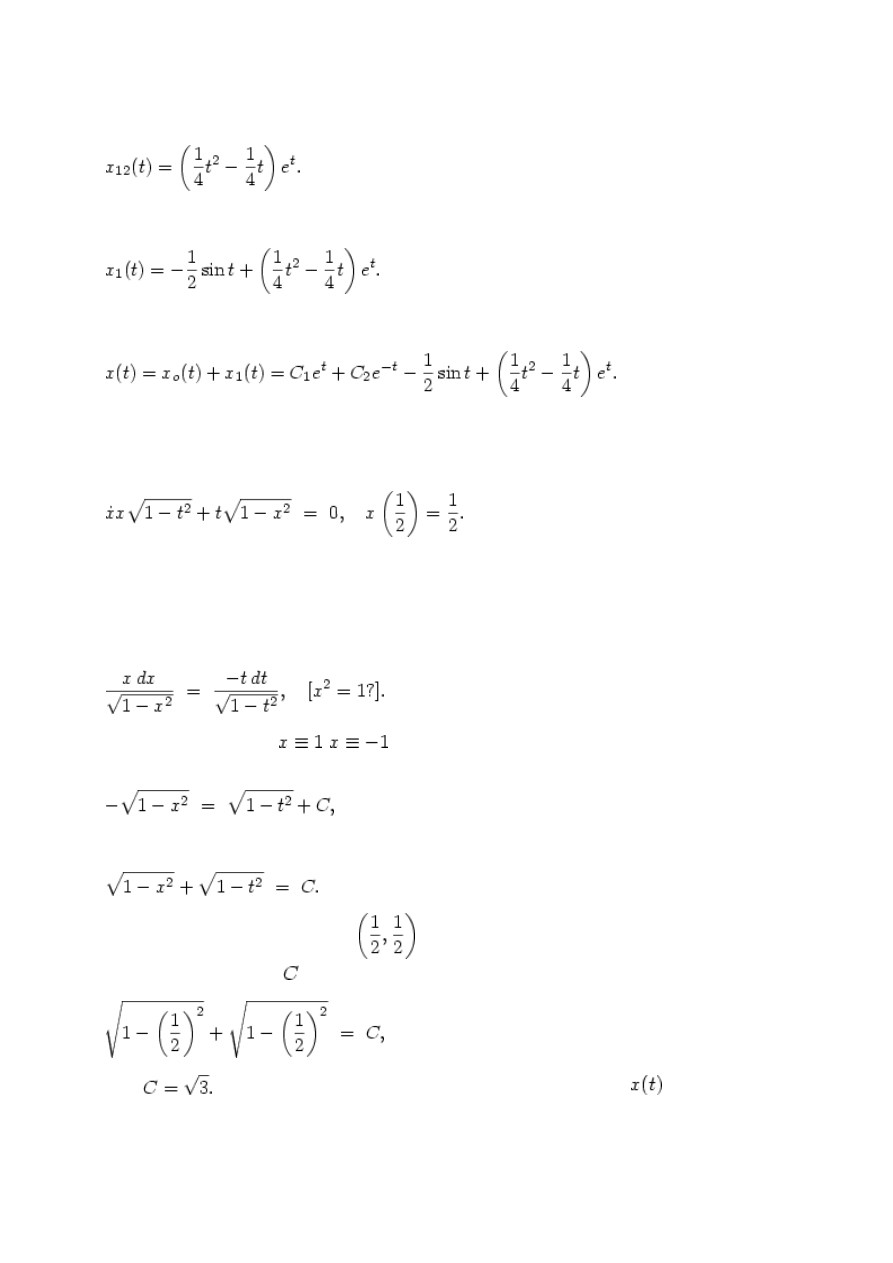
czyli

Sumując, dostajemy rozwi

zczególne wyjściowego równania niejednorodnego:

ązanie s

Tak więc rozwiązanie ogólne naszego równania to:

Ć

WICZENIE

14.1.

Rozwiązać problem Cauchy'ego:

W

SKAZÓWKA

[

POKAŻ

]

Rozdzielamy zmienne w powyższym równaniu i dostajemy

R

OZWIĄZANIE

[

SCHOWAJ

]

(Zauważmy od razu, że

i

są rozwiązaniami naszego równania). Całkując

powyższą równość, mamy

zatem rozwiązanie ogólne równania (w postaci uwikłanej) jest dane jako

Krzywą przechodzącą przez punkt

wyznaczamy, wstawiając ten punkt do powyższego

równania i wyznaczając :

skąd

A zatem rozwiązanie

lemu Cauchy'ego jest funkcja

m prob

dana przez

równanie

Ć

WICZENIE

14.2.

iązać pro

Rozw

blem Cauchy'ego:

W

SKAZÓWKA

Ż

]

R

OZWIĄZANIE

[

SCHOWAJ

]

Rozdzielamy zmienne w naszym równaniu i dostajemy

[

POKA

(Zauważmy też, że

jest rozwiązaniem wyjściowego równania). Całkując, mamy

(dla wygody stałą dowolną zapisaliśmy, podobnie jak na wykładzie, jako

; możemy tak

zrobić, bo funkcja jest suriekcją na ). Z powyższego równania dostajemy zatem

Nasz warunek początkowy to

zatem wstawiamy do rozwiązania ogólnego punkt

i wyznaczamy :

skąd

i szukane rozwiązanie to

Ć

WICZENIE

14.3

Znaleźć krzywe, dla których odcinek stycznej zawarty między osiami współrzędnych jest

ności.

W

SKAZÓWKA

[

OKAŻ

]

HOWAJ

]

podzielony na połowy w punkcie stycz

P

R

OZWIĄZANIE

[

SC

<flash>file=am2.m14.c.r01.swf|width=375|height=375</flash>

Odcinek styczny do wykresu krzywej

Równanie stycznej w punkcie

to

Odcinek styczny do wykresu krzywej

to punkt

Punkt przecięcia stycznej z osią

gdzie

Podobnie, przecięcia stycznej z osią

to punkt

gdzie

Z warunków zadania wynika, że współrzędne punktu

mają być średnimi arytmetycznymi współrzędnyc

t

h punk ów

i

Tak więc

my

dostaje

Stąd dostajemy, że

Zapiszmy to równanie różniczkowe, mnożąc przez i

iennych na

zmieniając nazwy zm

i Dostaniemy równanie

To jest równanie o zmiennych rozdzielonych; rozwiązujemy je

(Zauważmy tu, że choć

jest rozwiązaniem powyższego

równania, to nie jest rozwiązaniem naszego zadania, trudno bowiem w tym przypadku mówić
o "odcinku stycznej między osiami"). Całkując, dostajemy

zatem

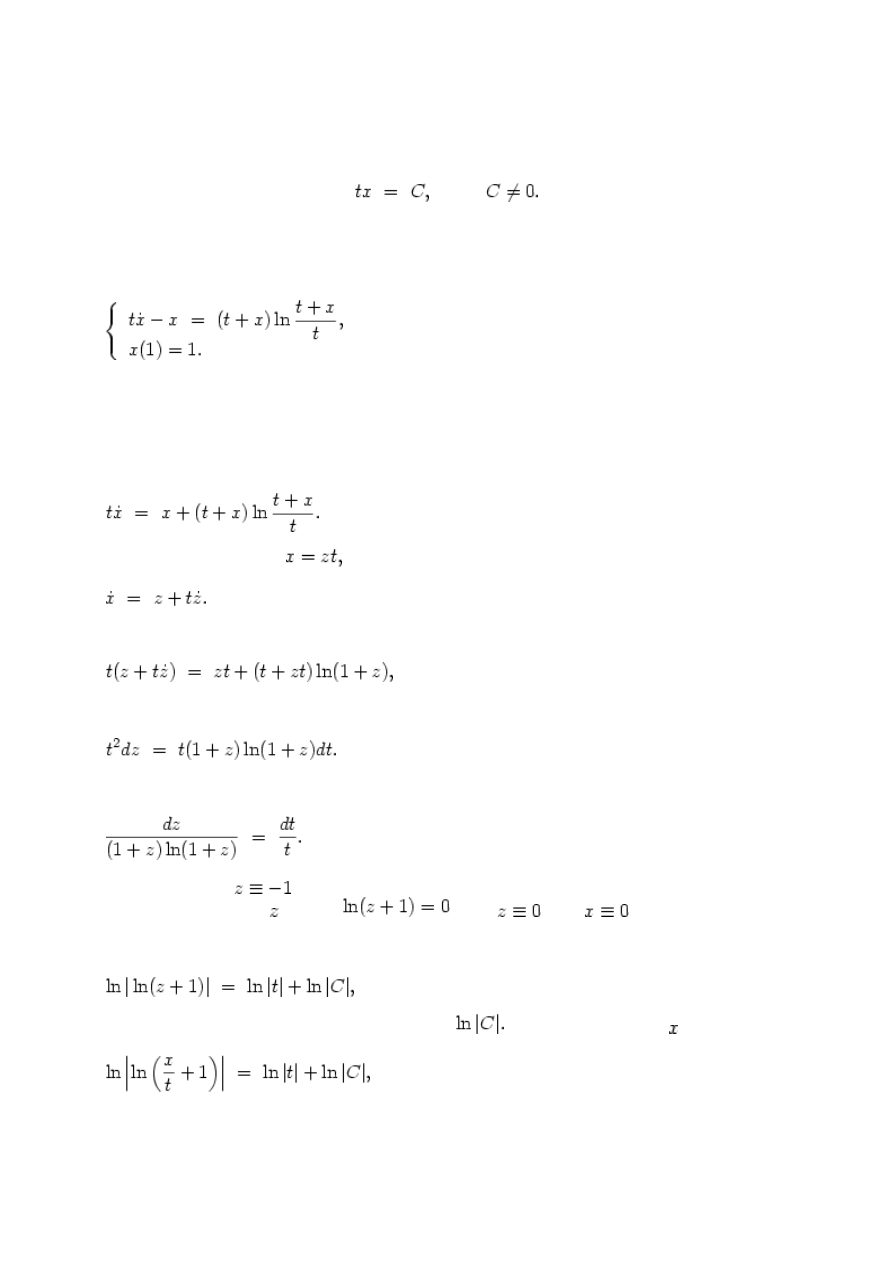
skąd dostajemy, że rozwiązaniem naszego zadania jest dowolna

krzywa spełniająca

ze stałą

Ć

WICZENIE

14.4.

Rozwiązać problem Cauchy'ego:

W

SKAZÓWKA

[

POKAŻ

]

Nasze równanie możemy zapisać w postaci

R

OZWIĄZANIE

[

SCHOWAJ

]

Stosujemy podstawienie

różniczkując, mamy

Podstawiając do naszego równania, mamy

skąd

Z powyższego równania dostajemy:

Zauważmy tu, że

nie jest rozwiązaniem tego równania (ze względu na dziedzinę

logarytmu), natomiast takie, że

, czyli

(czyli

) jest rozwiązaniem.

y

Całkując powyższą równość, dostajem

gdzie znów stałą d

zapisujemy w postaci

owolną

Wracając do zmiennej , mamy

czyli nasze rozwiązanie dane jest równaniem uwikłanym

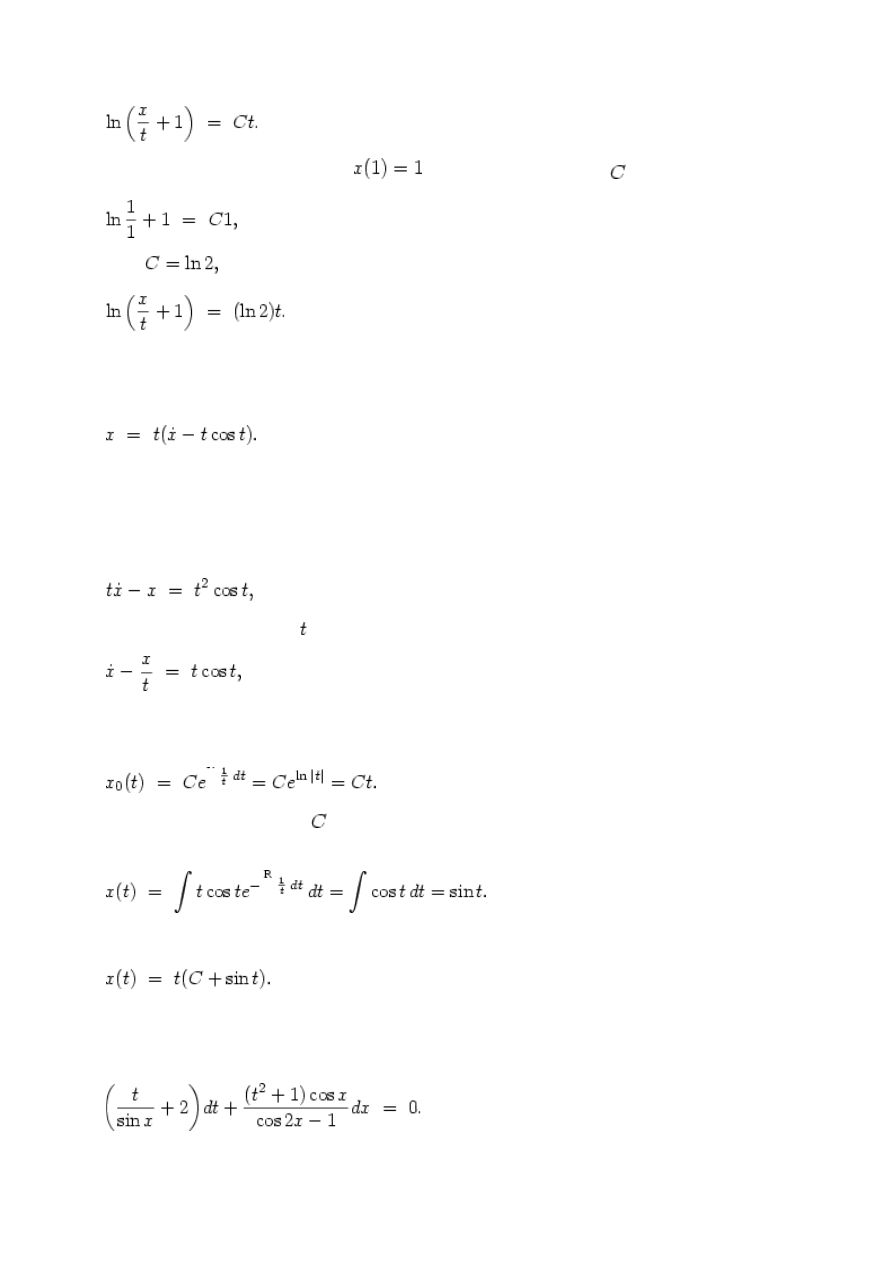
Rozwiązanie spełniające warunek

znajdujemy, wyznaczając z równania

czyli

zatem

ązanie to

szukane rozwi

Ć

WICZENIE

14.5.

ązać rów

Rozwi

nanie:

W

SKAZÓWKA

Ż

]

R

OZWIĄZANIE

[

SCHOWAJ

]

Nasze równanie po przekształceniu możemy zapisać jako

[

POKA

czyli po podzieleniu przez

a zatem faktycznie, mamy równanie liniowe niejednorodne. Rozwiązanie ogólne równania
jednorodnego ma postać

Moduł możemy opuścić, bo jest stałą dowolną. Rozwiązanie szczególne równania
niejednorodnego to w naszym przypadku

A zatem rozwiązaniem ogólnym naszego równania niejednorodnego jest

Ć

WICZENIE

14.6.

Znaleźć rozwiązanie ogólne równania:

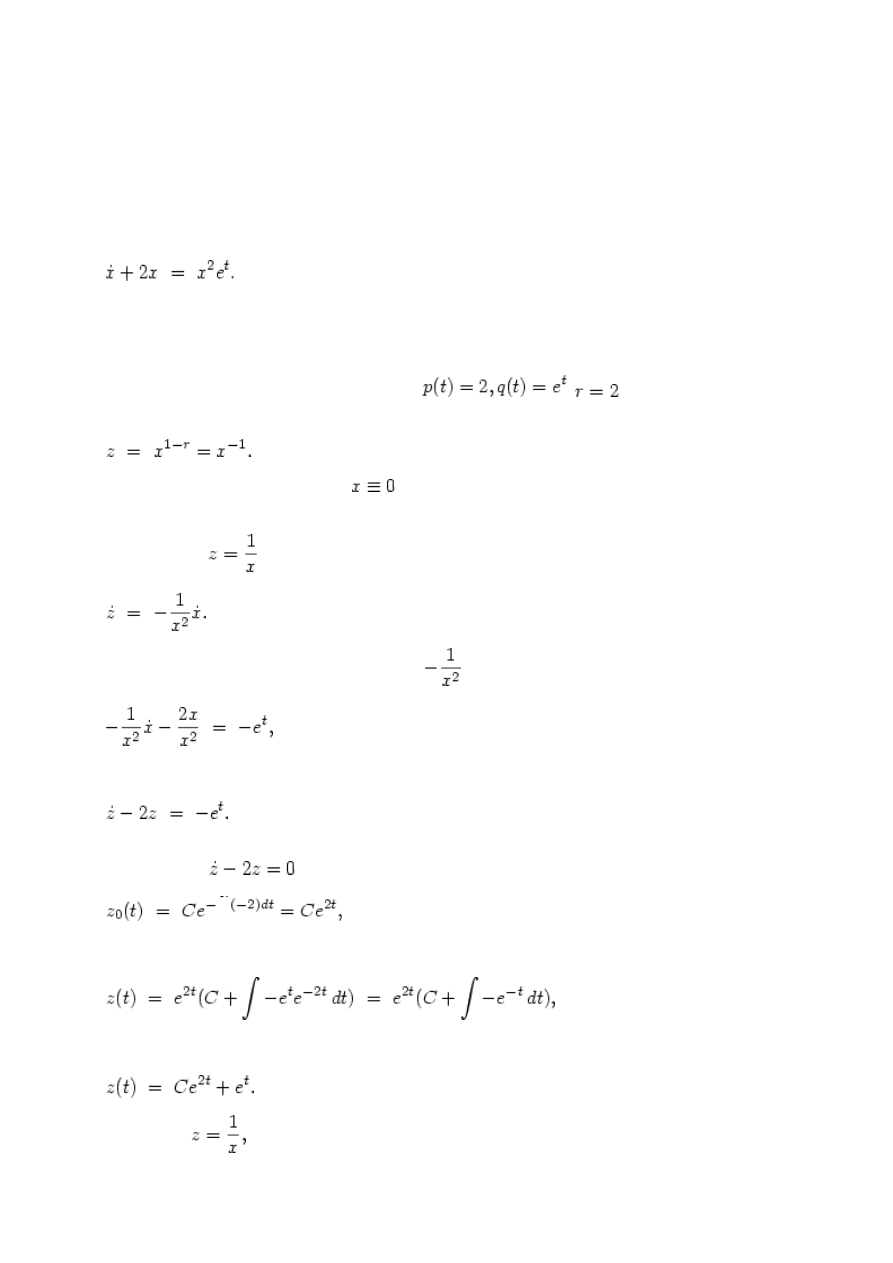
W

SKAZÓWKA

[

POKAŻ

]

R

OZWIĄZANIE

[

POKAŻ

]

Ć

WICZENIE

14.7.

Znaleźć rozwiązanie ogólne równania:

W

SKAZÓWKA

[

POKAŻ

]

R

OZWIĄZANIE

[

SCHOWAJ

]

Nasze równanie to równanie Bernoullego z

i

(oznaczenia jak na

wykładzie). Równanie rozwiązujemy, robiąc podstawienie

Osobno trzeba rozważyć sytuację

; widać, że ta funkcja jest rozwiązaniem naszego

równania.

Różniczkując

, dostajemy

Mnożymy nasze wyjściowe równanie przez

i dostajemy

czyli podstaw jąc

ia

To jest równanie liniowe niejednorodne rzędu pierwszego. Rozwiązanie ogólne równania
jednorodnego

to

zatem rozwiązanie ogólne równania niejednorodnego to

czyli

Stąd, skoro

rozwiązane możemy napisać jako

Ć

WICZENIE

14.8.

Znaleźć rozwiązanie równania:

które przech

rzez punkt

odzi p

i którego pochodna także

przechodzi przez punkt

W

SKAZÓWKA

[

POKAŻ

]

R

OZWIĄZANIE

[

POKAŻ

]

Ć

WICZENIE

14.9.

Znaleźć rozwiązanie równania:

W

SKAZÓWKA

[

POKAŻ

]

R

OZWIĄZANIE

[

SCHOWAJ

]

jemy równanie ogólne

Najpierw rozwiązu

Równanie charakterystyczne to

czyli

Rozwiązania tego równania to

A zatem, skoro mamy jeden rzeczywisty pierwiastek podwójny i dwa pierwiastki zespolone,
sprzężone, rozwiązanie ogólne równania jednorodnego to

Teraz szukamy rozwiązania szczególnego naszego równania. Ponieważ prawa strona
równania jest równa

a , jest podwójnym pierwiastkiem równania

charakterystycznego, rozwiązania szczególnego szukamy w postaci

Różniczkując, mamy

Wstawiając do równania, dostajemy

skąd

czyli

A więc rozwiązanie szczególne to

Rozwiązaniem ogólnym naszego równania jest zatem funkcja

Źródło:
"

http://osilek.mimuw.edu.pl/index.php?title=Analiza_matematyczna_2/%C4%86wiczenia_14:_Przegl%

r%C3%B3wna%C5%84_r%C3%B3%C5%BCniczkowych_zwyc

C4%85d_metod_ca%C5%82kowania_
zajnych

"