.
Kinematyka - jest dzia³em fizyki zajmuj¹cym siê opisem ruchu cia³
Ruch postêpowy
Ruch obrotowy
Zmiana kszta³tu cia³a
Uk³ad odniesienia
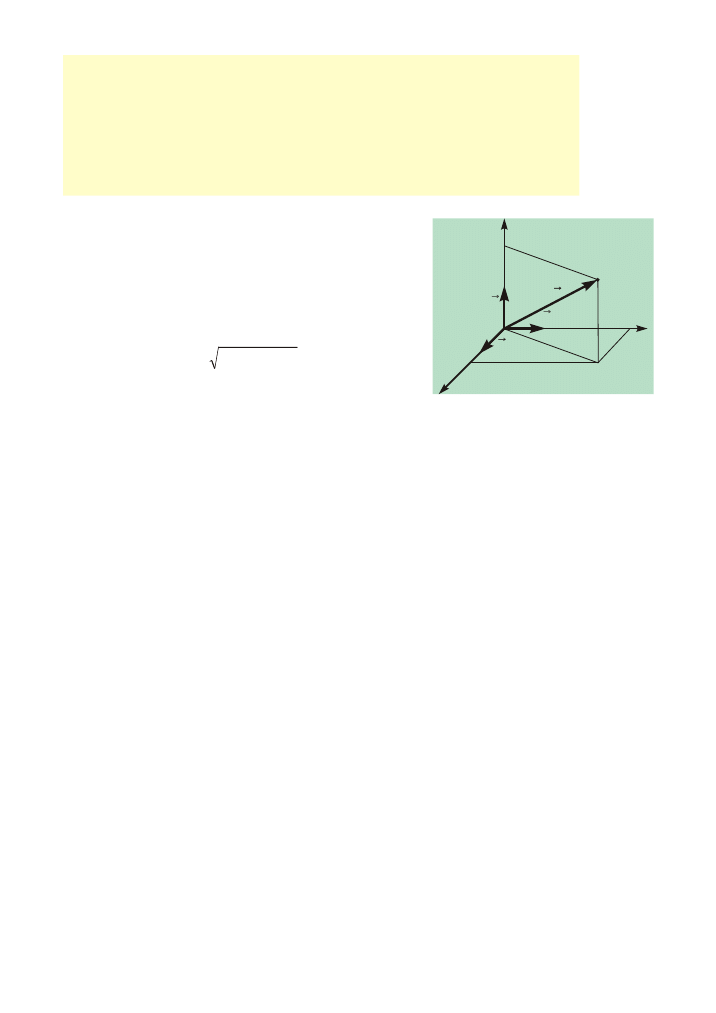
Wektor po³o¿enia lub promieñ wodz¹cy
Wektor po³o¿enia w uk³adzie kartezjañskim
r
r i
r j
r k
x i
y j
zk
®
®
®
®
®
®
®
=
+
+
=
+
+
x
y
z
r
r
x
y
z
=
=
+
+
®
| |
2
2
2
.
Z
X
Y
z
x
y
O
P(x,y,z)
i
k
r
j
Tor;
równanie toru
(
)
F x y z
, ,
= 0,
Np. x
y
R
2
2
2
+
=
,czyli
(
)
F x y z
x
y
R
, ,
=
+
-
=
2
2
2
0
Droga
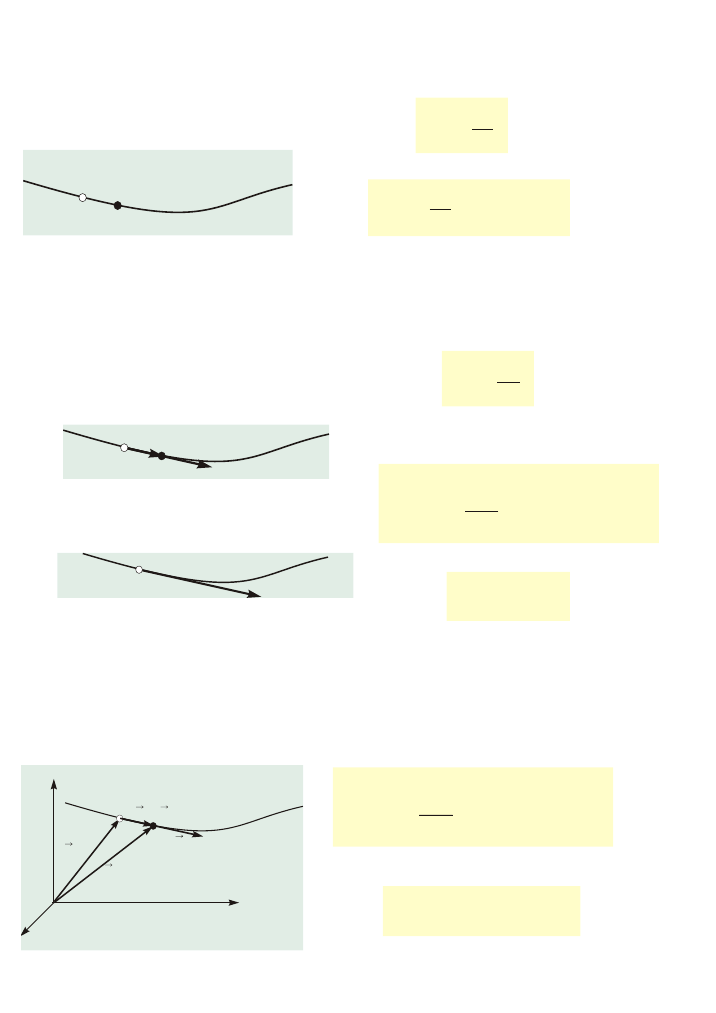
Wartoœæ prêdkoœci (prêdkoœæ)
Przemieszczenie
Prêdkoœæ (wektor prêdkoœci)
Wektor prêdkoœci w kartezjañskim uk³adzie wspó³rzêdnych
Ds
®
$s
v
v
®
=
( )
( ) $
t
t s
v
®
( )
t
Z
X
Y
O
r(t)
r(t+
Dt)
v
Ds.=Dr
v( )
t
s
t
=
D
D
, gdy Dt ® 0
Prêdkoœæ œrednia
v
œr
=
D
D
s
t
v
®
=
®
D
D
r
t
, gdy
Dt ® 0
v
®
=
®
D
D
s
t
, gdy
Dt ® 0
}
Ds
v
v
v
v
x
y
z
®
®
®
®
=
+
+
i
j
k
r
r
v
œr
=
D
D
s
t
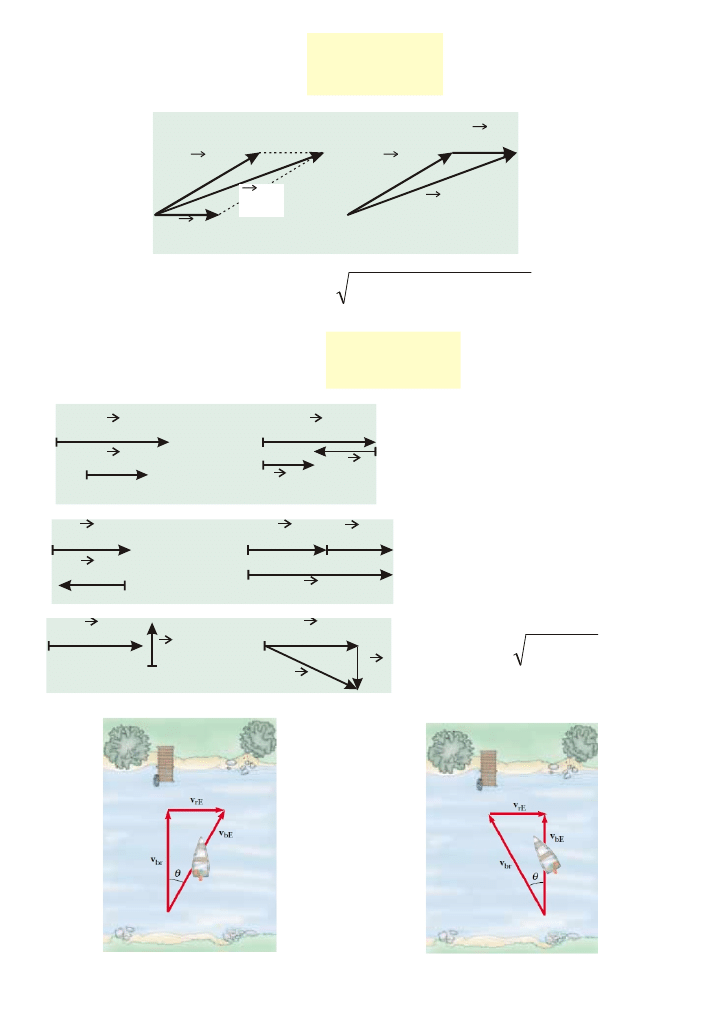
Dodawanie prêdkoœci
v
v
v
1
2
wyp
®
®
®
+
=
v
1
v
2
v
wyp
v
1
v
2
v
wyp
Prêdkoœæ wzglêdna
v
A
v
B
v
A
-v
B
v
A B
v
A
v
B
v
A
-v
B
v
A B
v
A
-v
B
v
A B
v
A
v
B
v
v
v
AB
A
B
=
-
v
v
v
AB
A
B
=
+
v
v
v
AB
A
2
B
2
=
+
v
v
v
AB
A
B
®
®
®
=
-
v
v
v
v v
wyp
=
+
-
1
2
2
2
1 2
2
cos a
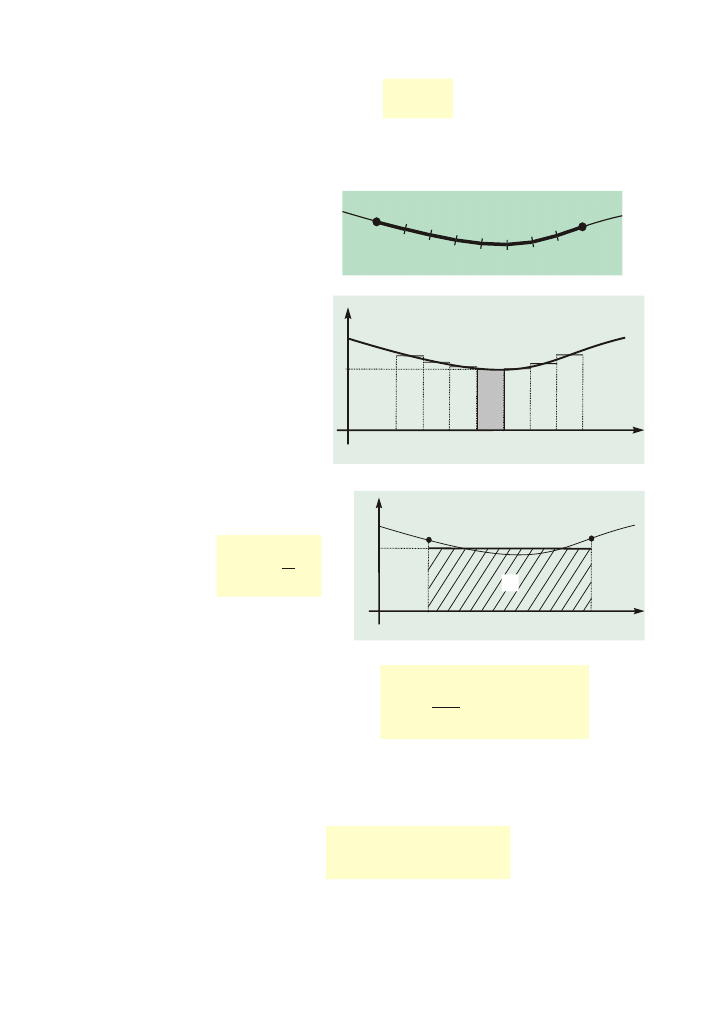
s
s
t
i
i
@
=
=
=
å
å
D
D
i
N
i
i
N
v
1
1
s
t
t
t
i
t
t
=
=
®
=
å
ò
lim
D
D
i
A
B
v
v d
i
i
N
0
1
Przyspieszenie w kartezjañskim uk³adzie wspó³rzêdnych
Droga
A
B
Ds
1
Ds
2
Ds
3
Ds
i
Ds
N
t
v(t)
t
A
t
B
Ds
1
Dt
2
v
i
Ds
N
Ds
2
Ds
i
Dt
1
Dt
i
Dt
N
Ruch jednostajny
Ruch niejednostajny
v=v(t)
v
œr
t
v(t)
t
A
t
B
s
Prêdkoœæ œrednia
v
œr
=
s
t
Przyspieszenie
a
t
®
®
=
D
D
v
,
gdy Dt ® 0
s=vt
a
a i
a
j
a k
®
®
®
®
=
+
+
x
y
z

Opis ruchu prostoliniowego w uk³adzie wspó³rzêdnych.
r
x
®
= [ , , ]
0 0 v
v
x
®
= [
, , ]
0 0 a
a
®
= [
, , ]
x
0 0
lub
v
v
®
= [ , , ]
0 0
a
a
®
= [ , , ]
0 0
Opis ruchu prostoliniowego bez uk³adu wspó³rzêdnych
– ruch jednostajny prostoliniowy: s
t
= v (v > 0, sta³a wartoœæ prêdkoœci),
– ruch jednostajnie przyspieszony prostoliniowy:
– ruch jednostajnie opóŸniony prostoliniowy:
Ruch prostoliniowy
i
X
a
0
x
v
r
v
v
®
®
=
i v > 0, gdy kierunki wektora v
®
i osi 0X zgodne
v < 0, gdy kierunki wektora v
®
i osi 0X przeciwne
a
a i
®
®
=
a > 0, gdy kierunki wektora a
®
i osi 0X zgodne
a < 0, gdy kierunki wektora a
®
i osi 0X przeciwne
v =
D
D
x
t
, gdy Dt ® 0
a
t
=
D
D
v
,
gdy Dt ® 0
Ruch jednostajny prostoliniowy
a = 0
v
const
=
x x
t
=
+
0
v
a = const v v
=
+
0
at
x x
t
at
=
+
+
0
0
2
2
v
Ruch jednostajnie zmienny
prostoliniowy
v
v
+ v
=
-
=
-
0
0
0
2
2
a
t
s
s
t
a
t
op
op
v
v
+ v
=
+
=
+
0
0
0
2
2
at
s
s
t
at
(a > 0, sta³e przyspieszenie cia³a)
(a
op
> 0, sta³e opóŸnienie cia³a).
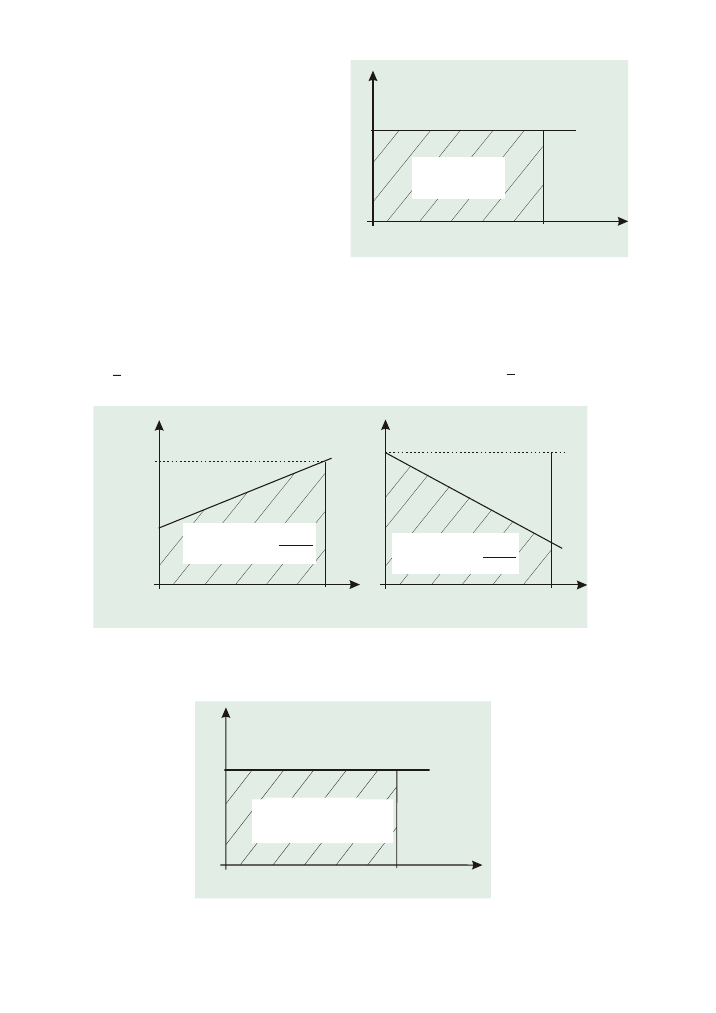
Graficzne wyznaczanie drogi
v
t
t
1
v
1
s = v t
1
1
0
Ruch jednostajny
Ruch jednostajnie zmienny
j
ednostajnie przyspieszony
jednostajnie opóŸniony
v +at
0
1
t
t
1
v
v
0
t
t
1
v
0
v
v = v
- a
t
0
op
s = v t -
1
0 1
a t
op 1
2
2
s = v t +
1
0 1
a t
1
2
2
v =
v +
a t
0
0
0
s
t
a t
t
1
0 1
0
1
0
1
1
2
=
+
+
-
v
v
v
[(
)
]
s
t
a
t
t
1
0 1
0
0
1
1
1
2
=
-
-
-
v
v
v
op
[
(
)]
a
t
t
1
1
0
a
v
v
=
+
0
1 1
a t
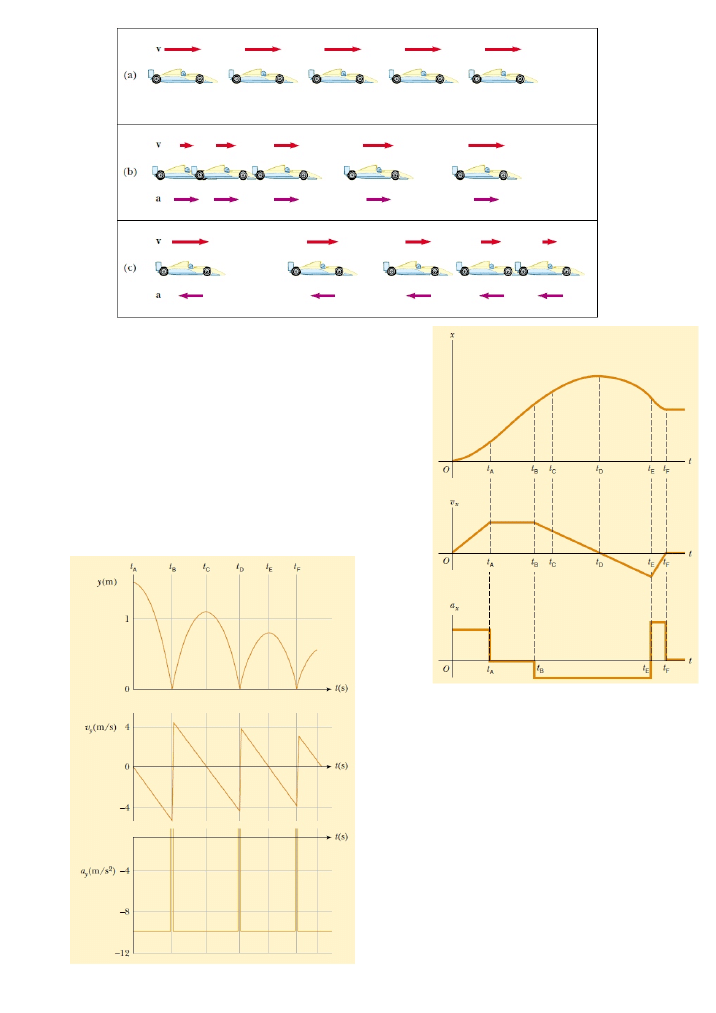
Zwi¹zek miêdzy po³o¿eniem prêdkoœci¹ i
przyspieszeniem w
ruchu prostoliniowym
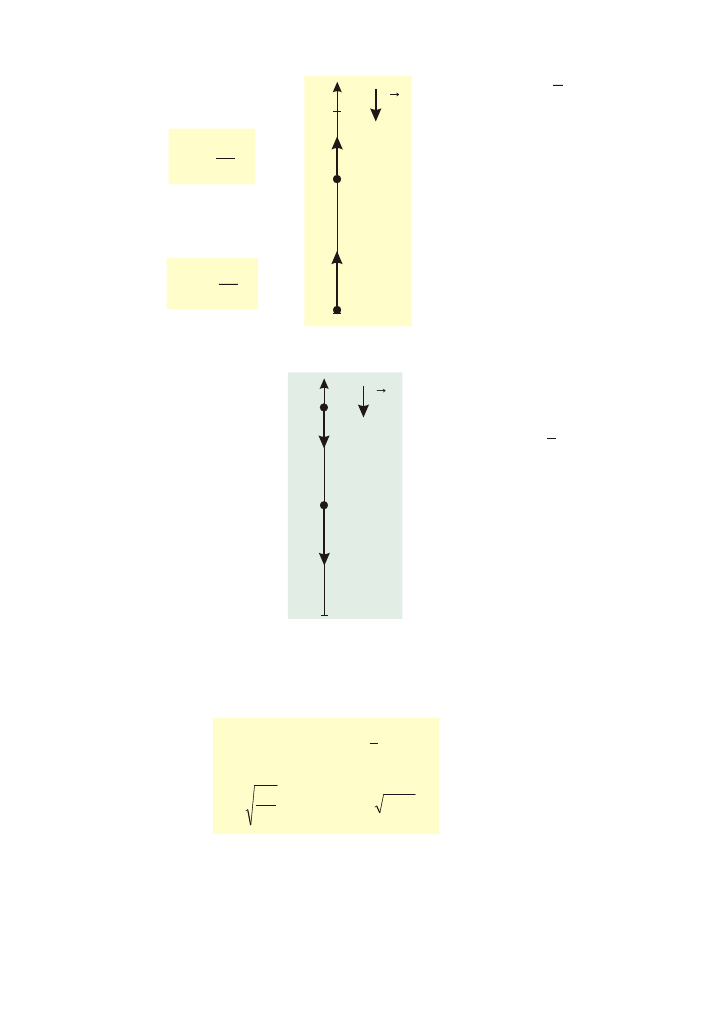
Rzuty
Rzut pionowy
Rzut pionowy w górê
Y
v
0
v
y
g
H
0
y
P(y)
y
t
g t
=
-
v
0
1
2
2
v
v
0
y
g t
=
-
H
g
=
v
0
2
2
t
g
H
0
v
=
Y
v
0
v
y
g
h
0
y
P(y)
y
h
t
g t
= -
-
v
0
1
2
2
v
v
0
y
g t
= -
-
Rzut pionowy w dó³
Spadek swobodny
v
k
k
= g t oraz H
g t
=
1
2
2
k
.
t
H
g
k
=
2
oraz v
k
= 2g H .
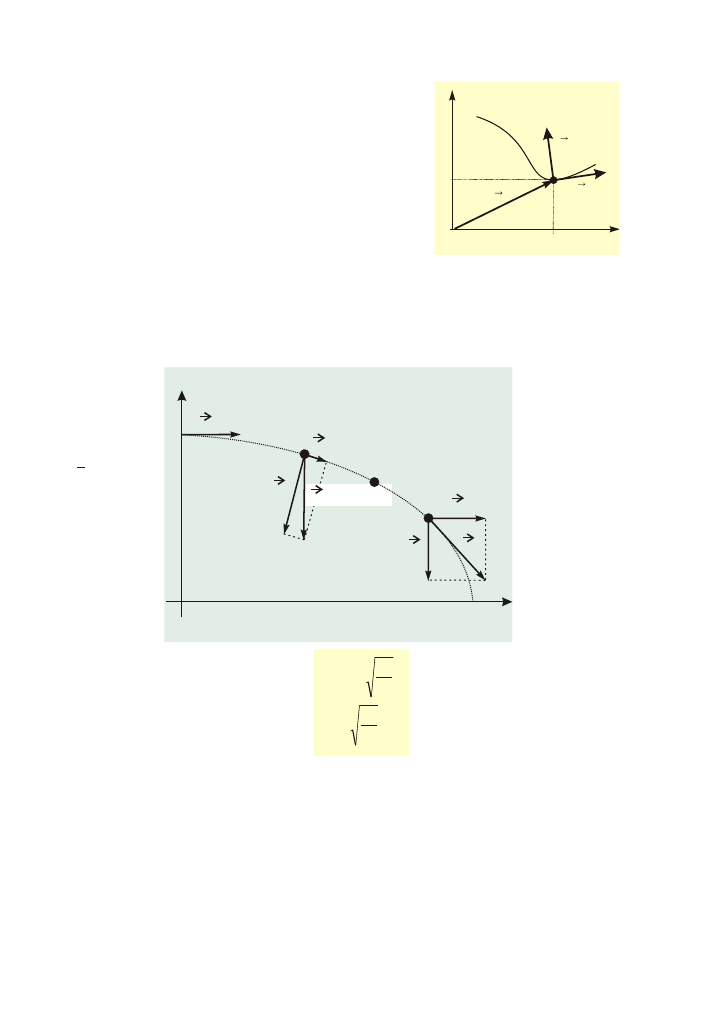
X
Y
x
y
O
r
a
v
Ruch p³aski
r
x y
®
= [ , , ]
0
v
v
v
x
y
®
= [
,
, ]
0
a
a
a
®
= [
,
, ]
x
y
0
Rzut poziomy
x
t
y
h
g t
=
=
-
v
0
1
2
2
X
Y
v
0
v
y
h
g
v
x
v
A
a
s
a
n
0
P(x,y)
OA
h
g
t
h
g
OA
=
=
v
0
2
2
v
v
v
0
x
y
g t
=
= -
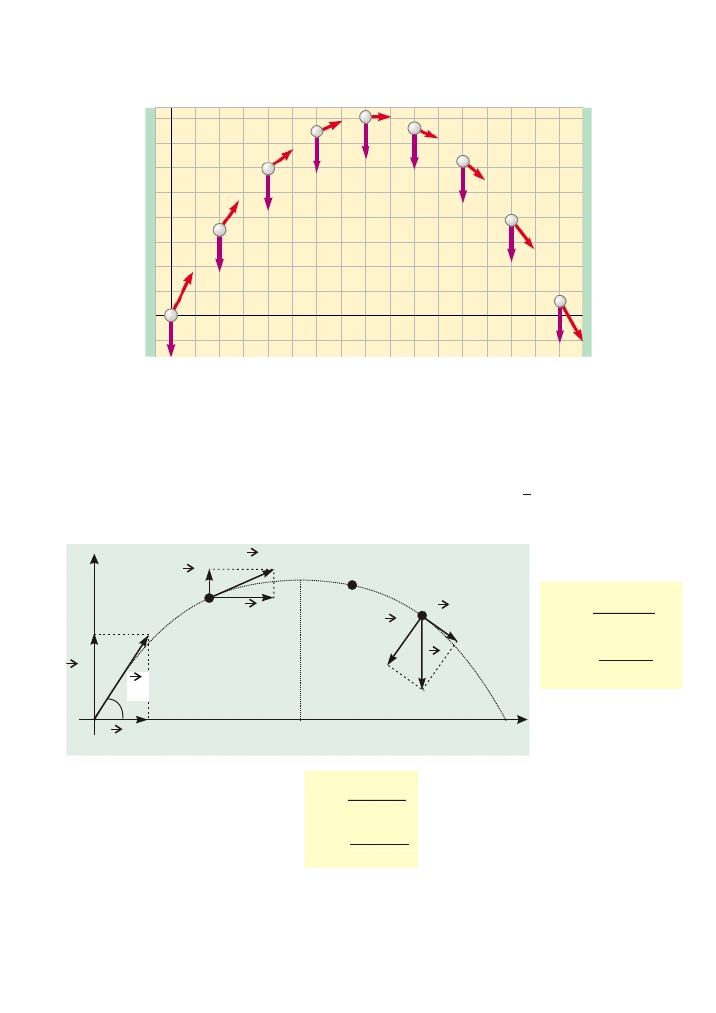
Rzut ukoœny
v
v
v
v
0
0
x
y
g t
=
=
-
cos
sin
a
a
x
t
y
t
g t
=
=
-
v
v
0
0
cos
sin
a
a
1
2
2
v
y
g
v
x
v
a
s
a
n
P(x,y)
X
Y
v
0
h
A
0
v
0x
v
0y
a
OA
g
t
g
OA
=
=
v
2v
0
2
sin
sin
2
0
a
a
h
g
t
g
=
=
v
v
0
2
h
sin
sin
2
0
2
a
a
v
v
v
v
0x
0
0y
0
=
=
cos
sin
a
a
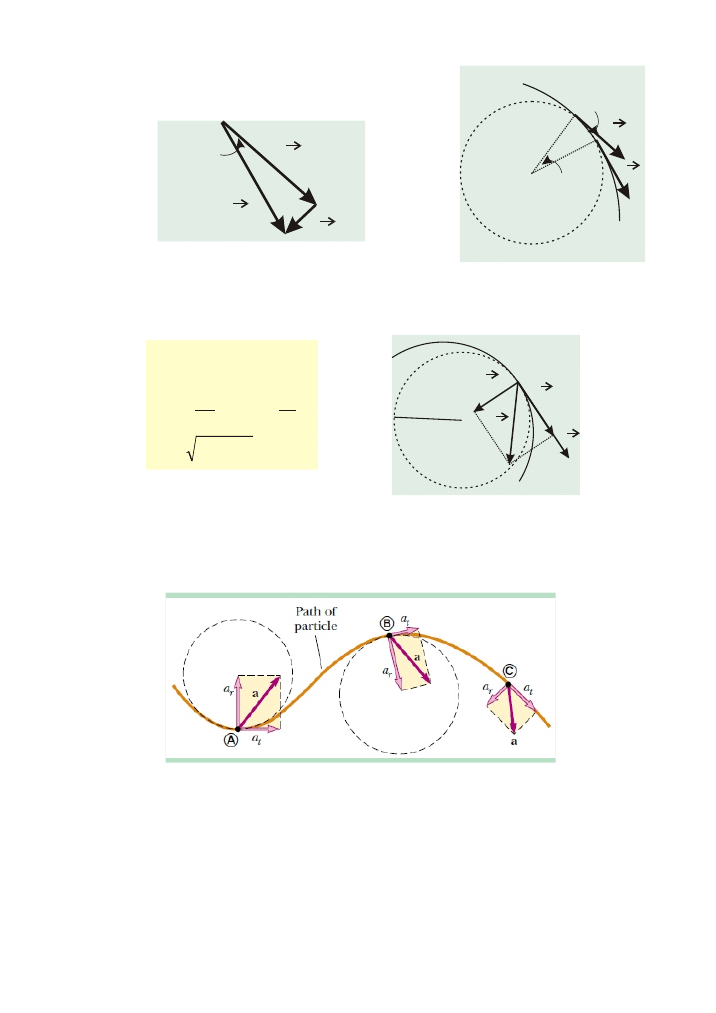
P
rzyspieszenie normalne i styczne
a
s
R
v
a
a
n
a
a
a
a
R
a
t
a
a
a
®
=
=
=
+
[
,
]
n
s
n
2
s
n
2
s
2
v
dv
d
=
R
v
1
Ds
v
2
Dj
Dj
v
1
v
2
Dv
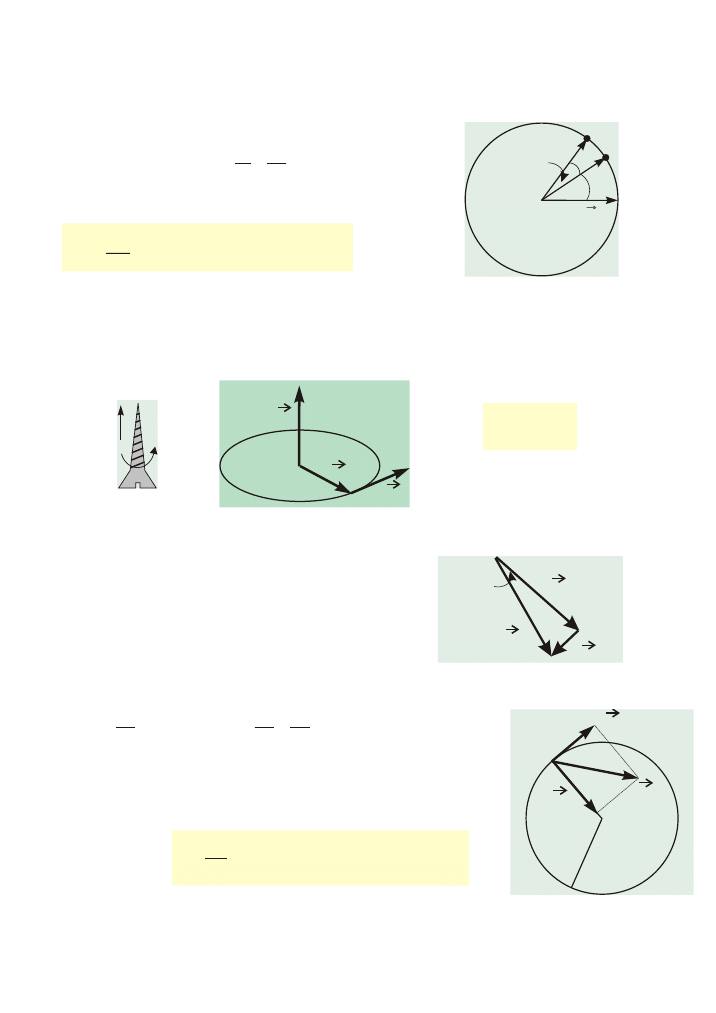
s
r
= j
D
D
D
D
s
t
t
r
=
j
Ruch po okrêgu
Prêdkoœæ k¹towa
w
j
=
D
Dt
,
gdy Dt ® 0
v = w r
r
j
Dj
O
Wektor prêdkoœci k¹towej
v
®
®
®
=
´
w r
O
r
v
w
e
w
=
D
Dt
,
gdy Dt ® 0 a
r
s
= e
Przyspieszenie i przyspieszenie k¹towe
a
a
r
r
n
d
v
=
=
=
2
2
w a
t
t
r
s
=
=
D
D
D
D
v
w
,
gdy Dt ® 0
a
a
s
a
d
O
r
Dj
v
1
v
2
Dv
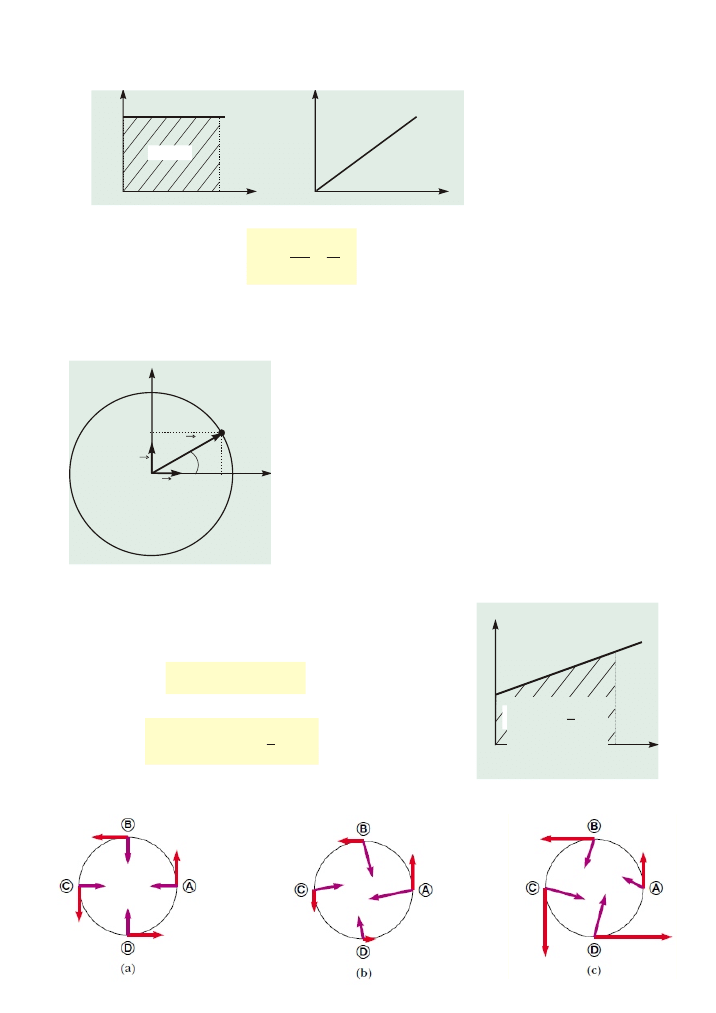
Okres ruchu
Ruch jednostajny po okrêgu w uk³adzie wspó³rzêdnych kartezjañskich
O
X
Y
r
j
y
x
j
i
wektor po³o¿enia kr¹¿¹cego cia³a,
r
x i
y j
®
®
®
=
+
x
r
t
= cos(
)
w
y
r
t
= sin(
)
w
Ruch jednostajnie zmienny po okrêgu
w w
e
=
+
0
t
j
j
w
e
0
=
+
+
0
2
1
2
t
t
O
t
w
j
w
e
=
+
0
2
1
2
t
t
w w
e
=
+
0
t
O
t
w
w = const
O
t
j
j =
w
t
j = w t
Ruch jednostajny po okrêgu
j
w
= t
T
f
=
=
2p
w
1
Wyszukiwarka
Podobne podstrony:
fizyka 2 KINEMATYKA PUNKTU MATERIALNEGO
FIZYKA KINEMATYKA(1)
Fizyka Kinematyka
Fizyka kinematyka i dynamika
Fizyka Kinematyka ) marca
Fizyka I Kinematyka 1
fizyka - kinematyka, budownictow, fizyka
fizyka kinematyka pr klucz
pawlikowski, fizyka, kinematyka
fizyka 2 KINEMATYKA PUNKTU MATERIALNEGO
,fizyka 1, Kinematyka układu materialnego
Sciaga - Fizyka Kompletne Wzory 2, KINEMATYKA
więcej podobnych podstron