
50. Reprezentacja liczb w pozycyjnym systemie liczbowym. Systemy
dwójkowy i szesnastkowy oraz ich zastosowania.
System dwójkowy
System dwójkowy (czyli binarny) to pozycyjny system liczbowy, którego podstawą są kolejne potęgi
dwójki. Został spopularyzowany przez
przedstawiane są jako suma potęg bazy (2) z odpowiednimi wagam
w tym przypadku tylko dwie: 0 i 1. Każda liczba naturalna dodatnia ma zatem reprezentację postaci:
, gdzie
Powszechnie używany w elektronice cyfrowej
na prostą implementację sprzętową odpowiadającą zazwyczaj stanom
zminimalizowanie przekłamań danych. Co za tym idzie, przyjął się też w
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako
jest mnożnikiem kolejnej potęgi podstawy systemu.
Np. liczba zapisana w dziesiętnym systemie liczbowym
postać 1010, gdyż:
Liczby w systemach niedziesiętnych
dziesiętnym, a oznaczającym podstawę danego systemu. W celu podkreślenia, że liczba jest
dziesiętna można również napisać obok niej indeks. Np.
W systemie dwójkowym można przedstawiać również
dziesiętne o podstawie 2 można zapisać j
Ułamek zwykły zapisujemy:
50. Reprezentacja liczb w pozycyjnym systemie liczbowym. Systemy
dwójkowy i szesnastkowy oraz ich zastosowania.
System dwójkowy (czyli binarny) to pozycyjny system liczbowy, którego podstawą są kolejne potęgi
dwójki. Został spopularyzowany przez Wilhelma Gotfrieda Leibniza w wieku XVII.
przedstawiane są jako suma potęg bazy (2) z odpowiednimi wagami reprezentowanymi przez cyfry
w tym przypadku tylko dwie: 0 i 1. Każda liczba naturalna dodatnia ma zatem reprezentację postaci:
elektronice cyfrowej, gdzie minimalizacja liczby stanów (do dwóch) pozwala
mentację sprzętową odpowiadającą zazwyczaj stanom wyłączony
zminimalizowanie przekłamań danych. Co za tym idzie, przyjął się też w informatyce
Jak w każdym pozycyjnym systemie liczbowym, liczby zapisuje się tu jako ciągi cyfr
jest mnożnikiem kolejnej potęgi podstawy systemu.
dziesiętnym systemie liczbowym jako 10, w systemie dwójkowym przybiera
Liczby w systemach niedziesiętnych oznacza się czasami indeksem dolnym zapisanym w systemie
dziesiętnym, a oznaczającym podstawę danego systemu. W celu podkreślenia, że liczba jest
dziesiętna można również napisać obok niej indeks. Np.
W systemie dwójkowym można przedstawiać również liczby rzeczywiste. Na przykład
o podstawie 2 można zapisać jako:
50. Reprezentacja liczb w pozycyjnym systemie liczbowym. Systemy
System dwójkowy (czyli binarny) to pozycyjny system liczbowy, którego podstawą są kolejne potęgi
Wilhelma Gotfrieda Leibniza w wieku XVII. Liczby naturalne
i reprezentowanymi przez cyfry –
w tym przypadku tylko dwie: 0 i 1. Każda liczba naturalna dodatnia ma zatem reprezentację postaci:
, gdzie minimalizacja liczby stanów (do dwóch) pozwala
wyłączony i włączony oraz
informatyce.
cyfr, z których każda
, w systemie dwójkowym przybiera
oznacza się czasami indeksem dolnym zapisanym w systemie
dziesiętnym, a oznaczającym podstawę danego systemu. W celu podkreślenia, że liczba jest
. Na przykład liczby
Jak w prosty sposób znajdować reprezentacje dwójkowe liczb naturalnych? Są dwie proste metody.
Załóżmy, że chodzi nam o przedstawienie dwójkowe liczby
Znajdujemy największą liczbę
od
wartość , a następnie kolejno dla wszystkich mniejszych potęg dwójki sprawdzamy, czy
mieszczą się one w tym, co zostało z
zero, a jeśli mieści się, to dopisujemy jedynkę i
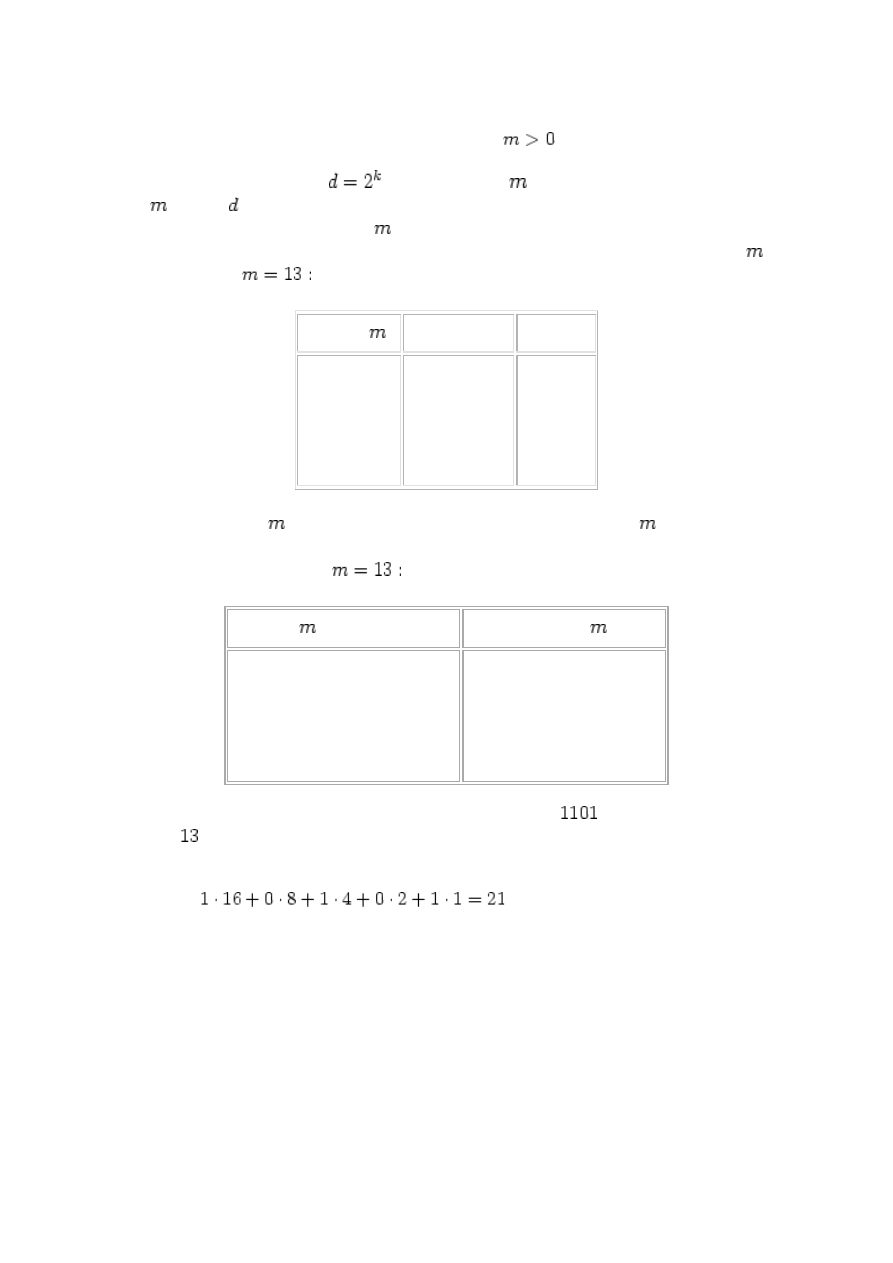
Przykładowo dla
zostało z
Zaczynamy od liczby
, a następnie dopóki m jest większe od zera dzielimy
kolejno otrzymywane reszty. Ciąg reszt odczytany od końca da nam poszukiwaną reprezentację.
Przykładowo dla tego samego
zostało z
po dzieleniu przez 2
Ciąg reszt z ostatniej kolumny czytany od dołu do góry
dwójkową
.
W odwrotną stronę trudno podać lepszą metodę niż proste dodanie kolejnych potęg dwójki, zatem
np. 10101, to
System szesnastkowy
System szesnastkowy to system różny od tego, którego używamy na co dzień.
bazuje na liczbie 16, a więc potrzebuje 16 znaków za pomocą, których można zapisać dowolną liczbę.
Szesnastkowy system liczbowy jest właściwy komputerom, ponieważ pozwala na zapis większych
liczb w mniejszych przestrzeniach pamięci.
Jak w prosty sposób znajdować reprezentacje dwójkowe liczb naturalnych? Są dwie proste metody.
Załóżmy, że chodzi nam o przedstawienie dwójkowe liczby
.
Znajdujemy największą liczbę
nieprzekraczającą
. Piszemy jedynkę, odejmujemy
, a następnie kolejno dla wszystkich mniejszych potęg dwójki sprawdzamy, czy
mieszczą się one w tym, co zostało z
. Jeśli dana potęga dwójki nie mieści się, to dopisujemy
zero, a jeśli mieści się, to dopisujemy jedynkę i odejmujemy tę wartość od tego, co zostało z
zostało z
potega dwójki wypisano
13
5
1
1
0
8
4
2
1
1
11
110
1101
, a następnie dopóki m jest większe od zera dzielimy
otrzymywane reszty. Ciąg reszt odczytany od końca da nam poszukiwaną reprezentację.
Przykładowo dla tego samego
po dzieleniu przez 2 reszta z dzielenia
przez 2
13
6
3
1
0
Ciąg reszt z ostatniej kolumny czytany od dołu do góry daje właśnie
, czyli reprezentację
W odwrotną stronę trudno podać lepszą metodę niż proste dodanie kolejnych potęg dwójki, zatem
System szesnastkowy to system różny od tego, którego używamy na co dzień. Różni się o tyle, że
bazuje na liczbie 16, a więc potrzebuje 16 znaków za pomocą, których można zapisać dowolną liczbę.
Szesnastkowy system liczbowy jest właściwy komputerom, ponieważ pozwala na zapis większych
liczb w mniejszych przestrzeniach pamięci.
Jak w prosty sposób znajdować reprezentacje dwójkowe liczb naturalnych? Są dwie proste metody.
jedynkę, odejmujemy
, a następnie kolejno dla wszystkich mniejszych potęg dwójki sprawdzamy, czy
. Jeśli dana potęga dwójki nie mieści się, to dopisujemy
odejmujemy tę wartość od tego, co zostało z
.
przez 2, zapisując
otrzymywane reszty. Ciąg reszt odczytany od końca da nam poszukiwaną reprezentację.
przez 2
1
0
1
1
, czyli reprezentację
W odwrotną stronę trudno podać lepszą metodę niż proste dodanie kolejnych potęg dwójki, zatem
Różni się o tyle, że
bazuje na liczbie 16, a więc potrzebuje 16 znaków za pomocą, których można zapisać dowolną liczbę.
Szesnastkowy system liczbowy jest właściwy komputerom, ponieważ pozwala na zapis większych
W systemie szesnastkowym wyróżniamy 16 cyfr:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Cyfry 0-9 mają te same wartości co w systemie dziesiętnym, natomiast litery odpowiadają
następującym wartościom: A = 10, B = 11, C = 12, D = 13, E = 14 oraz F = 15.
Zapis liczby całkowitej w systemie heksadecymalnym ma postać:
a
i-1
a
i-2
... a
2
a
1
a
0
= a
i-1
· 16
i-1
+ a
i-2
· 16
i-2
+ ... + a
2
· 16
2
+ a
1
· 16
1
+ a
0
· 16
0
Konwersji (zamiany) liczby w systemie dziesiętnym na system heksadecymalny można dokonać
poprzez wielokrotne dzielenie przez 16 i spisywanie reszt z dzielenia. Przy ilorazie równym zero
należy spisać ostatnią resztę i odczytać ciąg utworzony z reszt zaczynając od ostatniej, kończąc na
pierwszej. Utworzony w ten sposób ciąg jest reprezentacją szesnastkową liczby dziesiętnej.
Np. liczba zapisana w dziesiętnym systemie liczbowym jako 1000, w systemie szesnastkowym
przybiera postać 3E8, gdyż:
Szesnastkowy system liczbowy stosuje się w informatyce, w przypadku programowania
niskopoziomowego, sterowania hardwarem, wyboru adresów.
Adresy IP np. w wersji 6 są podawane w pozycyjnym systemie szesnastkowym np.:
3ffe:0902:0012:0000:0000:0000:0000:0000/48.
W języku składu stron internetowych i/lub programach edycji stron WWW system szesnastkowy
stosowany jest do oznaczania kolorów.
51. Podstawowe prawa algebry Boole'a.
Algebra Boole'a – struktura algebraiczna stosowana w matematyce, informatyce teoretycznej oraz
elektronice cyfrowej. Jej nazwa pochodzi od nazwiska angielskiego matematyka, filozofa i logika
George'a Boole'a.
Typowymi przykładami algebr Boole'a są: rodzina wszystkich podzbiorów ustalonego zbioru wraz
działaniami na zbiorach jako operacjami algebry oraz dwuelementowa algebra wartości logicznych
{0, 1} z działaniami koniunkcji, alternatywy i negacji.
Algebra Boole'a to struktura algebraiczna , w której i są działaniami dwuargumentowymi, ˜ jest
operacją jednoargumentową, a 0 i 1 są wyróżnionymi różnymi elementami zbioru , spełniająca
następujące warunki dla wszystkich :
łączność
rozdzielność
przemienność
absorpcja
pochłanianie
Algebra Boole'a jest to struktura matematyczna złożona z trzech działań binarnych:
- ∨ (lub, or, alternatywa)
- ∧ (i, and, koniunkcja)
- ~ (nie, not, przeczenie logiczne, negacja
oraz wyróżnionych elementów 0 (fałsz), 1 (prawda)
Negacja
To zdanie mające postać nieprawda, że p
jest jako:
(lub
). Negację można zdefiniować ściślej jako
określone w zbiorze zdań, które każdemu zdaniu p przyporządkowuje zdanie
Negację zdania p uważa się za prawdziwą, gdy zdanie
zdanie p jest prawdziwe.
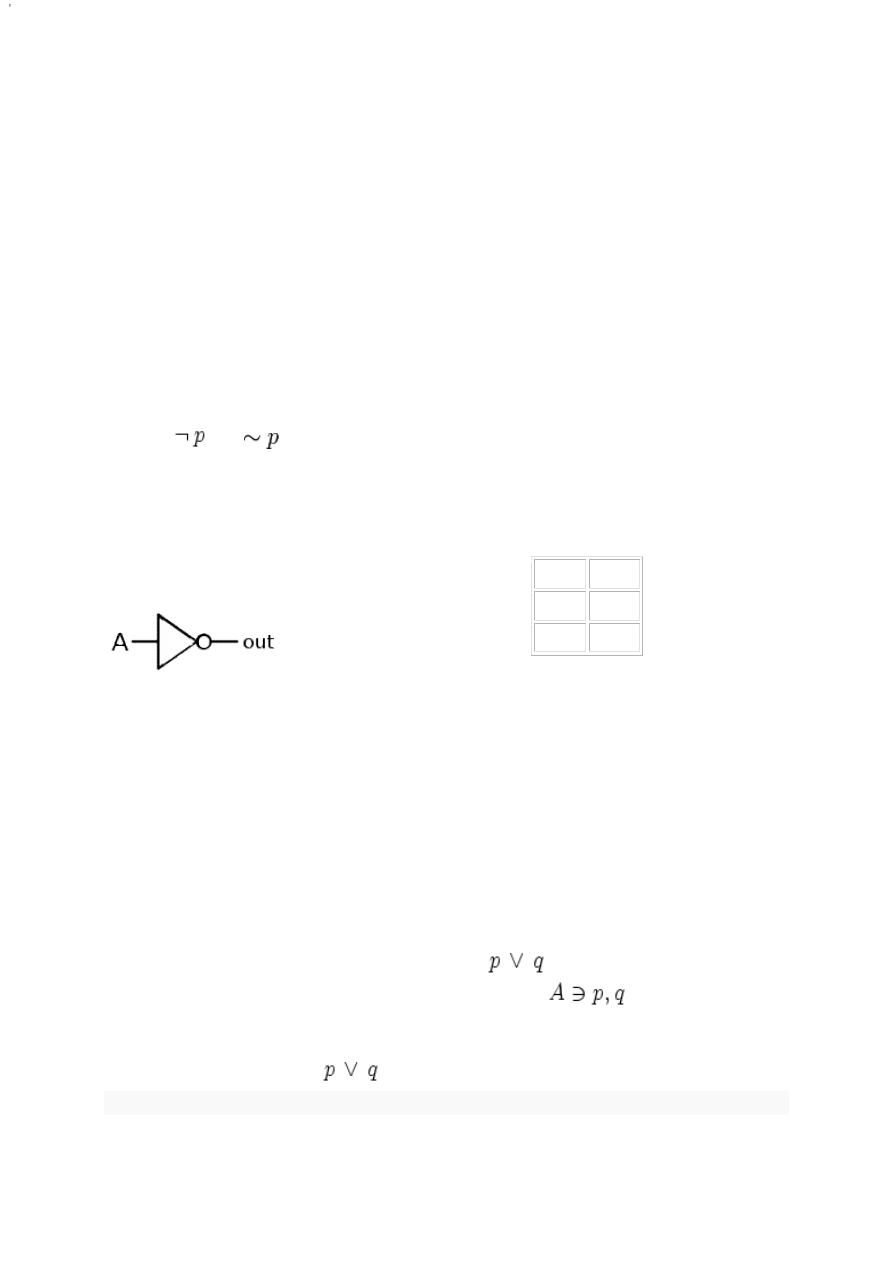
Symbol negacji jako bramki logicznej
Alternatywa lub suma logiczna
To w logice matematycznej:
1. Działanie dwuargumentowe
zdaniowych, które zdaniom (funkcjom zdaniowym)
prawdziwe wtedy i tylko wtedy gdy prawdziwe jest przynajmniej jedno ze zdań (funkcji)
2. Dwuargumentowy spójnik zdaniowy, oznaczany
wyżej zdefiniowanemu działaniu określonemu w zbiorze
definicji różni się tym, że jest definiowany na poziomie syntaktycznym, dzięki czemu unika
się określania jego dziedziny.
3. Zdanie logiczne postaci
Algebra Boole'a jest to struktura matematyczna złożona z trzech działań binarnych:
, negacja)
ionych elementów 0 (fałsz), 1 (prawda).
nieprawda, że p, gdzie p jest zdaniem. W rachunku zdań
). Negację można zdefiniować ściślej jako jednoargumentowe działanie
określone w zbiorze zdań, które każdemu zdaniu p przyporządkowuje zdanie nieprawda, że p
uważa się za prawdziwą, gdy zdanie p jest fałszywe, zaś za fałszywą, gdy
bramki logicznej:
suma logiczna
Działanie dwuargumentowe określone w dowolnym zbiorze zdań bądź w zbiorze funkcji
zdaniowych, które zdaniom (funkcjom zdaniowym) p i q przypisuje zdanie (funkcję zdaniową)
prawdziwe wtedy i tylko wtedy gdy prawdziwe jest przynajmniej jedno ze zdań (funkcji)
Dwuargumentowy spójnik zdaniowy, oznaczany
o znaczeniu odpowiadającemu
yżej zdefiniowanemu działaniu określonemu w zbiorze
. Od poprzedniej
definicji różni się tym, że jest definiowany na poziomie syntaktycznym, dzięki czemu unika
się określania jego dziedziny.
, gdzie p i q są zdaniami.
p
¬ p
0
1
1
0
Algebra Boole'a jest to struktura matematyczna złożona z trzech działań binarnych:
rachunku zdań negacja zapisywana
jednoargumentowe działanie
nieprawda, że p.
jest fałszywe, zaś za fałszywą, gdy
rze zdań bądź w zbiorze funkcji
rzypisuje zdanie (funkcję zdaniową)
prawdziwe wtedy i tylko wtedy gdy prawdziwe jest przynajmniej jedno ze zdań (funkcji) p i q
o znaczeniu odpowiadającemu
. Od poprzedniej
definicji różni się tym, że jest definiowany na poziomie syntaktycznym, dzięki czemu unika
Alternatywa pozostaje w ścisłym związku z
zdanie utworzone z innych zdań przy użyciu alternatywy jest też nazywane
Alternatywa jest prawdziwa, jeżeli którekolwiek z jej zdań składowych jest prawdziwe. W przeciwnym
razie alternatywa zdań jest fałszywa
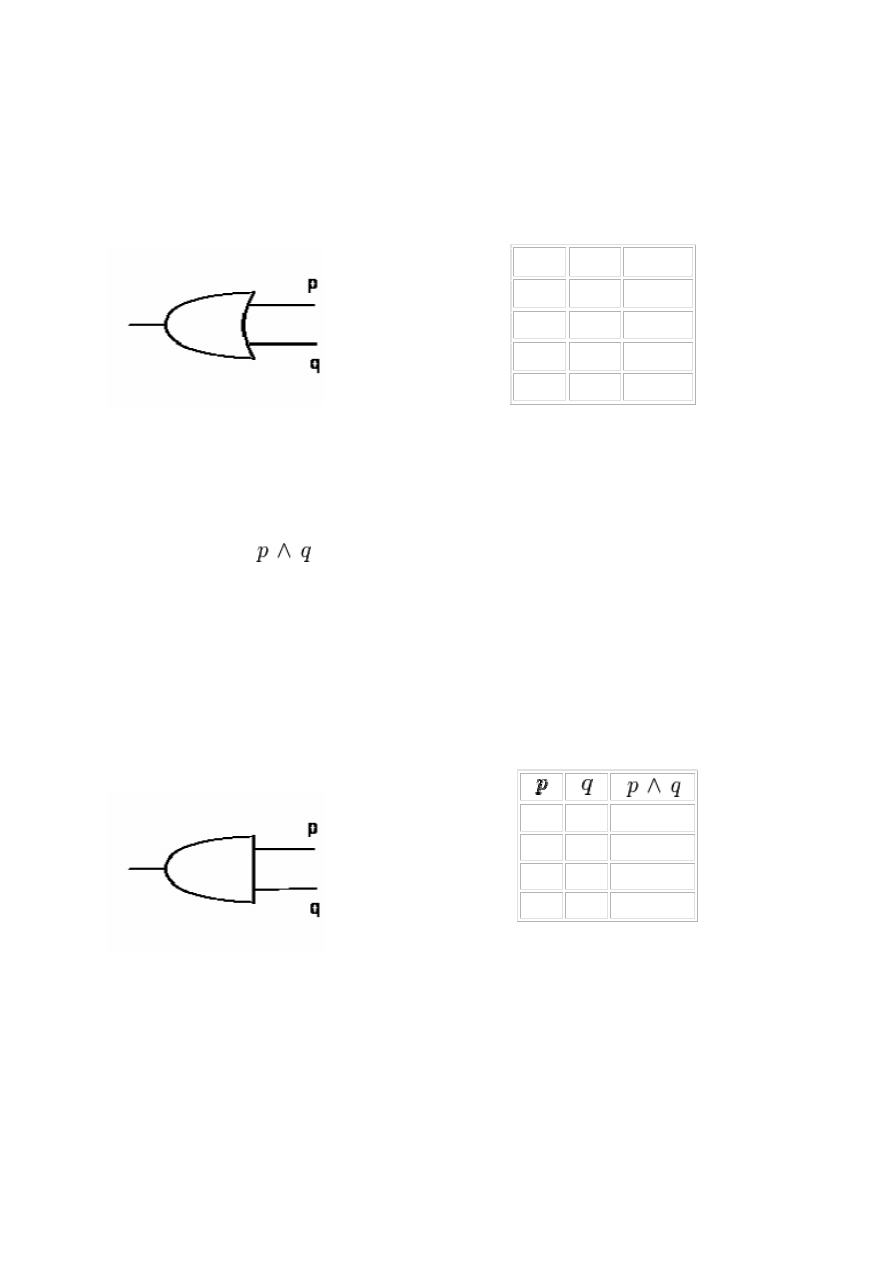
Symbol alternatywy jako bramki logicznej
Koniunkcja
To zdanie złożone mające postać
się symbolicznie jako:
. Przez koniunkcję rozumie się też zdanie mające postać
Koniunkcję można zdefiniować precyzyjniej jako dwuargumentowe działanie określone w zbiorze
zdań, które zdaniom p, q przyporządkowuje zdanie
Działanie to pozostaje w ścisłym związku z działaniem
Dlatego zdanie utworzone z innych zdań za pomocą koniunkcji jest też nazywane
logicznym. Koniunkcję zdań uznaje się za prawdziwą wtedy i tylko wtedy, gdy oba zdania
prawdziwe.
Symbol koniunkcji jako bramki logicznej
52. Reprezentacja w pamięci danych typów prostych i złożonych.
Typem prostym nazywamy wartość, która nie może być
jest to typ, który przyjmuje wartości proste
Alternatywa pozostaje w ścisłym związku z dodawaniem zbiorów (patrz algebra zbiorów
zdanie utworzone z innych zdań przy użyciu alternatywy jest też nazywane sumą logiczną
, jeżeli którekolwiek z jej zdań składowych jest prawdziwe. W przeciwnym
fałszywa.
bramki logicznej:
złożone mające postać p i q , gdzie p, q są zdaniami. W rachunku zdań koniunkcję zapisuje
. Przez koniunkcję rozumie się też zdanie mające postać
Koniunkcję można zdefiniować precyzyjniej jako dwuargumentowe działanie określone w zbiorze
przyporządkowuje zdanie p i .
Działanie to pozostaje w ścisłym związku z działaniem przekroju zbiorów (patrz algebra zbiorów
Dlatego zdanie utworzone z innych zdań za pomocą koniunkcji jest też nazywane
. Koniunkcję zdań uznaje się za prawdziwą wtedy i tylko wtedy, gdy oba zdania
bramki logicznej:
52. Reprezentacja w pamięci danych typów prostych i złożonych.
nazywamy wartość, która nie może być rozłożona na prostsze wartości.
jest to typ, który przyjmuje wartości proste.
p
q
p
0
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
algebra zbiorów). Dlatego
sumą logiczną.
, jeżeli którekolwiek z jej zdań składowych jest prawdziwe. W przeciwnym
koniunkcję zapisuje
. Przez koniunkcję rozumie się też zdanie mające postać p(1) i ... i p(n).
Koniunkcję można zdefiniować precyzyjniej jako dwuargumentowe działanie określone w zbiorze
algebra zbiorów).
Dlatego zdanie utworzone z innych zdań za pomocą koniunkcji jest też nazywane iloczynem
. Koniunkcję zdań uznaje się za prawdziwą wtedy i tylko wtedy, gdy oba zdania p, q są
52. Reprezentacja w pamięci danych typów prostych i złożonych.
rozłożona na prostsze wartości. Typ prosty
p ∨ q
0
1
1
1
0
0
0
1
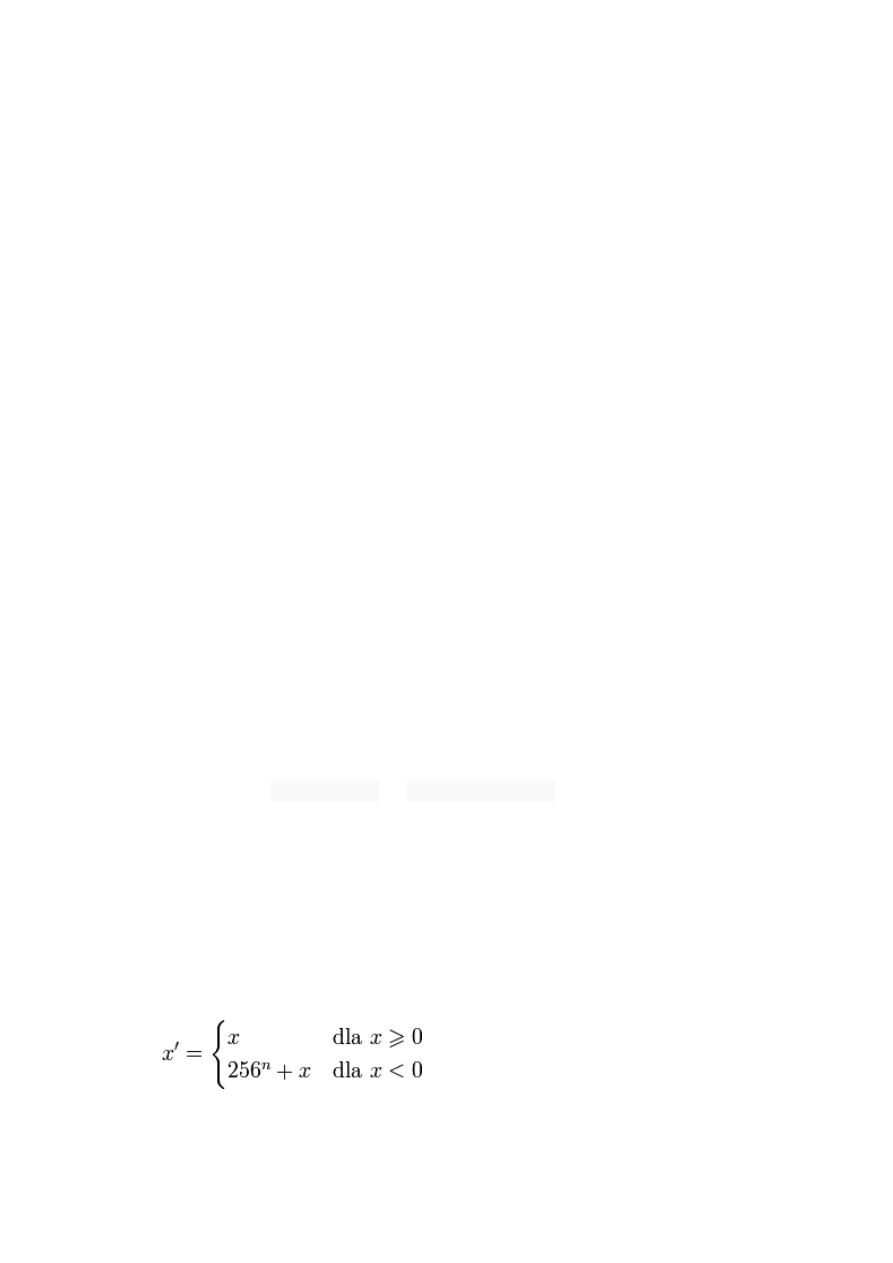
Wartością złożoną nazywamy wartość, która może być rozłożona na prostsze wartości. Typ złożony
jest to typ, który przyjmuje wartości złożone.
Dane w pamięci komputera czy też w plikach zapisane są w postaci ciągu tzw. bajtów. Każdy bajt
składa się z ośmiu cyfr systemu dwójkowego (0 lub 1), zwanych bitami. Pojedynczy bajt może
przyjmować jeden z 2
8
= 256 stanów. Powstaje konieczność zakodowania liczb w postaci ciągu
bajtów, tak aby komputery mogły je przetwarzać. Można to zrobić na wiele sposobów, jednak w
praktyce używanych jest kilka standardów:
Liczby naturalne
Typ obejmujący przedział liczb naturalnych z zerem zwany jest w informatyce liczbami bez
znaku (ang. unsigned integers).
Liczby naturalne z przedziału 0-255 można po prostu zakodować jako wartość jednego bajta.
Na dwóch bajtach można już zapisać liczby naturalne z przedziału 0-65535 (mamy do
dyspozycji 65536 = 256
2
stanów). Każdą taką liczbę można zapisać w postaci x = 256h + l,
gdzie horaz l to wartości tzw. starszego bajta i młodszego bajta, z przedziału od 0 do 255 każda.
Wartości te można zapisać w pamięci na dwa sposoby: albo pierwszy jest starszy bajt, a drugi
młodszy (tzw. notacja big endian), albo odwrotnie (little endian).
Na czterech bajtach można zapisać liczby z przedziału 0 – 4 294 967 295. Analogicznie jak poprzednio,
przedstawienie danej liczby w systemie 256-kowym pozycyjnym jakox = 256
3
a
3
+ 256
2
a
2
+
256a
1
+ a
0
uzyskuje się cztery bajty a
3
,a
2
,a
1
,a
0
. Kolejność ich zapisu w pamięci, tak jak poprzednio,
zależy od procesora – w przypadku little endian od bajta a
0
do a
3
, w przypadku big endian –
odwrotnie.
Do niektórych zastosowań konieczne są jeszcze większe liczby naturalne, np. zapisywane na 8 bajtach
(w rodzinie C oznaczane unsigned _int64 lub unsigned long long int).
Liczby całkowite
Typ obejmujący przedział liczb całkowitych zwany jest w informatyce liczbami ze
znakiem (ang. signed integers).
Stosuje się tzw. kod uzupełnień do dwóch (U2). Liczba x, która ma zostać zapisana w postaci n bajtów
jest przekształcana w następujący sposób:
Następnie liczba x' jest zapisywana jako liczba naturalna. W ten sposób na jednym bajcie można
zapisywać liczby z przedziału od − 128
liczby od − 2
8n − 1
do 2
8n − 1
− 1 włącznie.
Liczby rzeczywiste
Liczby rzeczywiste mogą być zapisywane jako:
liczby stałoprzecinkowe, kiedy liczba mnożona jest przez pewną ustaloną z góry stałą, po
czym zaokrąglana do najbliższej liczby całkowitej i jako taka zapisywana;
liczby zmiennoprzecinkowe, gdy stała dobierana jest w zależności od kodowanej liczby, co czyni
tę metodę uniwersalniejszą.
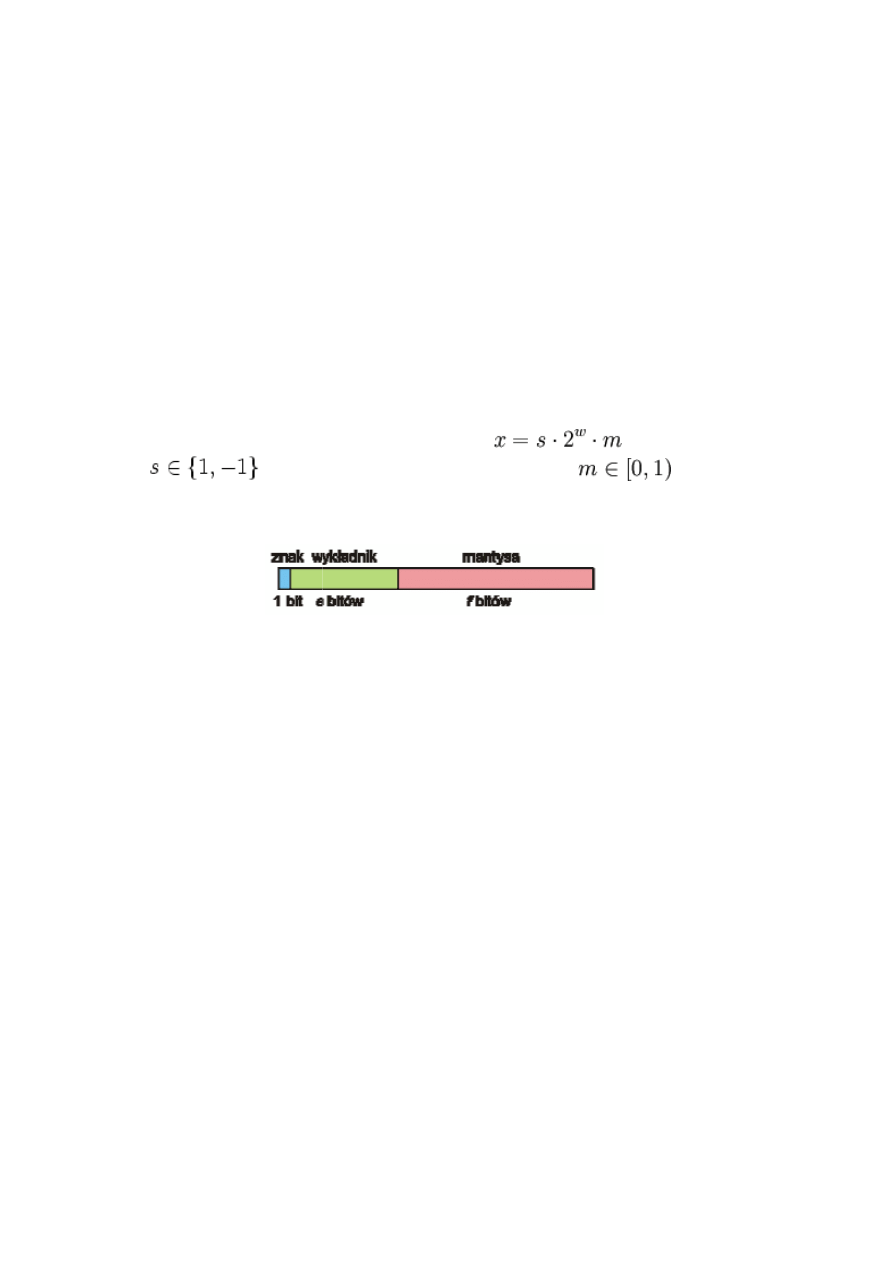
Powszechnie stosuje się zmiennoprzecinkowy zapis liczby rzeczywistej w standardzie
Przybliżenie liczby rzeczywistej jest zapisywane w postaci
gdzie
jest nazywany
Zero, które można by zakodować na wiele sposobów jest kodowane jako
Znak jest zapisywany jako jeden bit, równy 0 dla
każda inna liczba całkowita w kodzie uzupełnień do dwóch. Mantysa jest mnożona przez
liczba bitów przeznaczona na nią i zapisywana jako liczba naturalna.
Całość zajmuje kolejnych 4, 8 albo 16 bajtów (w zależno
umieszczenia w pamięci jest zależna od procesora, identycznie jak w przypadku liczb naturalnych i
całkowitych.
Znaki
Typ znakowy – jeden z podstawowych
celu przechowywanie pojedynczego
W językach C i C++ typ ten jest po prostu
przypadku signed char; lub bez znaku, dla
kwalifikatora signed/unsigned rodzaj liczby zależy od implementacji)
Typ string jest często reprezentowany w postaci tablicy char
jest zapisywana jako liczba naturalna. W ten sposób na jednym bajcie można
− 128 do 127, na dwóch od − 32768 do 32767, i ogólnie na
włącznie.
Liczby rzeczywiste mogą być zapisywane jako:
, kiedy liczba mnożona jest przez pewną ustaloną z góry stałą, po
do najbliższej liczby całkowitej i jako taka zapisywana;
, gdy stała dobierana jest w zależności od kodowanej liczby, co czyni
Powszechnie stosuje się zmiennoprzecinkowy zapis liczby rzeczywistej w standardzie
Przybliżenie liczby rzeczywistej jest zapisywane w postaci
,
jest nazywany znakiem, w – wykładnikiem, a
Zero, które można by zakodować na wiele sposobów jest kodowane jako s = + 1,w
Znak jest zapisywany jako jeden bit, równy 0 dla s = + 1 i 1 dla s = − 1. Wykładnik jest zapisywany jak
każda inna liczba całkowita w kodzie uzupełnień do dwóch. Mantysa jest mnożona przez
liczba bitów przeznaczona na nią i zapisywana jako liczba naturalna.
Całość zajmuje kolejnych 4, 8 albo 16 bajtów (w zależności od wymaganej precyzji). Ich kolejność
umieszczenia w pamięci jest zależna od procesora, identycznie jak w przypadku liczb naturalnych i
jeden z podstawowych typów danych w wielu językach programowania
pojedynczego znaku tekstu.
typ ten jest po prostu jednobajtową liczbą całkowitą (może być ona ze
; lub bez znaku, dla unsigned char; w przypadku nie podania
rodzaj liczby zależy od implementacji)
ntowany w postaci tablicy char’ów.
jest zapisywana jako liczba naturalna. W ten sposób na jednym bajcie można
, i ogólnie nan bajtach
, kiedy liczba mnożona jest przez pewną ustaloną z góry stałą, po
, gdy stała dobierana jest w zależności od kodowanej liczby, co czyni
Powszechnie stosuje się zmiennoprzecinkowy zapis liczby rzeczywistej w standardzie IEEE 754.
– mantysą.
w = 0,m = 0.
. Wykładnik jest zapisywany jak
każda inna liczba całkowita w kodzie uzupełnień do dwóch. Mantysa jest mnożona przez 2
f
, gdzie f to
ści od wymaganej precyzji). Ich kolejność
umieszczenia w pamięci jest zależna od procesora, identycznie jak w przypadku liczb naturalnych i
językach programowania, mający na
(może być ona ze znakiem, w
; w przypadku nie podania
Wyszukiwarka
Podobne podstrony:
48 49 50 51 52 53 54 55 56 57
11 2003 51 52
10 1995 51 52
50 51
51 52 (2)
fiszki 01 51 i 52
51 52
50 51
ei 04 2002 s 50 51
51 52
49,50,51
50 51 307 POL ED02 2001
50, 51
51 52
50 51
50-51, Uczelnia, Administracja publiczna, Jan Boć 'Administracja publiczna'
50 51 307-POL-ED02-2001
więcej podobnych podstron