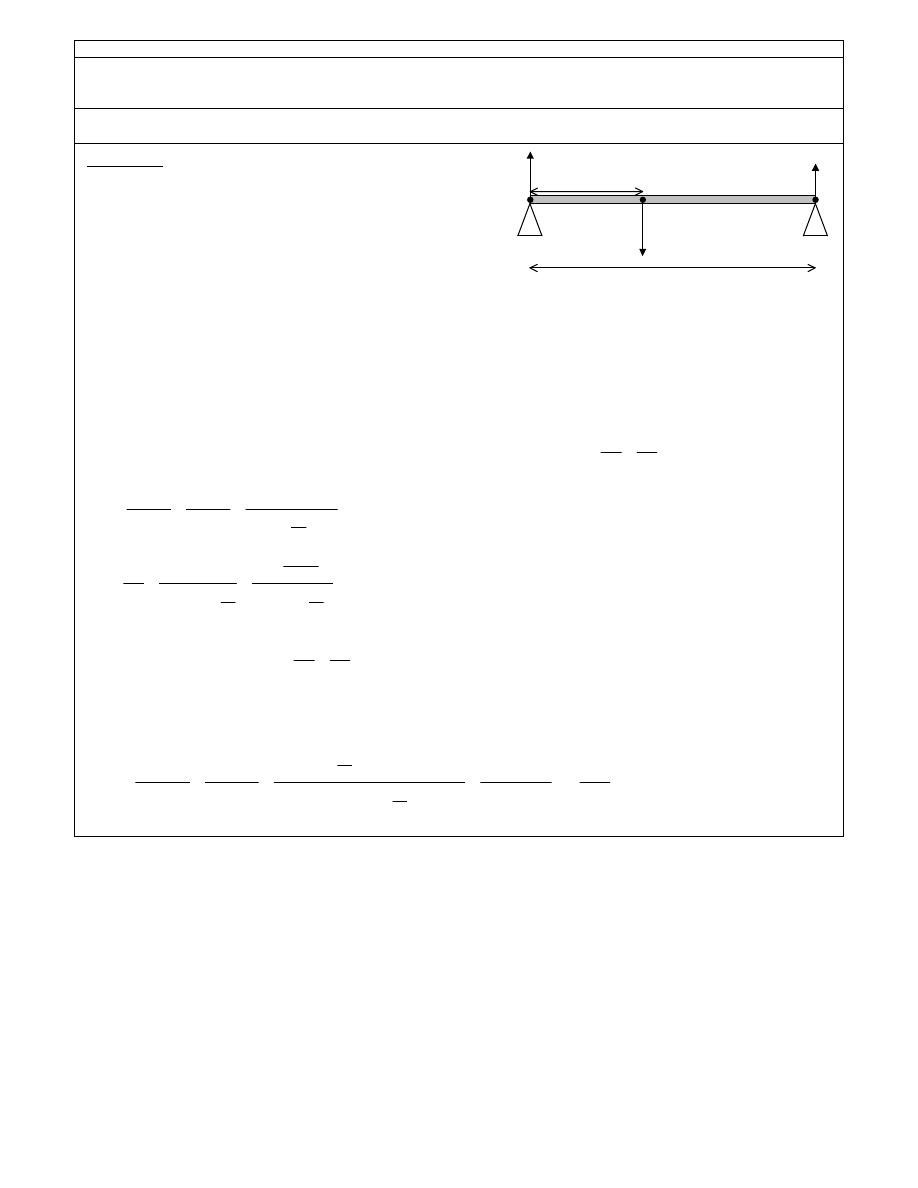
ZAD. 48
Gdzie znajduje si rodek ci ko ci niejednorodnej belki o długo ci l = 2 m, je li podpory na jej ko cach s obci one siłami F
1
=
1200 N i F
2
= 800 N? Oblicz mas m belki.
Odp.: x = 0,8 m , m = 200 kg
Rozwi zanie:
Na belk działaj trzy siły: ci ar Q przyło ony w rodku ci ko ci
odległym o x od lewego ko ca belki oraz siły reakcji podpór R
1
oraz R
2
przyło one do ko ców belki. Warto ci sił R
1
oraz R
2
s odpowiednio
R
1
= F
1
, R
2
= F
2
, a ich zwroty przeciwne do zwrotów sił F
1,
F
2
(zasada akcji i reakcji).
Belka jest nieruchoma, wi c (zgodnie z pierwszym prawem statyki)
wypadkowa wszystkich sił działaj cych na belk musi by równa zeru.
Napiszemy:
mg
R
R
Q
R
R
=
+
=
+
2
1
2
1
(1)
Belka nie obraca si , wi c (zgodnie z drugim prawem statyki), wypadkowy moment siły wzgl dem dowolnej osi musi by równy
zeru. O obrotu mo na na wybra w dowolnym miejscu.
a) Niech o obrotu przechodzi przez rodek ci ko ci belki. Wtedy
( )
−
=
=
+
)
2
(
)
1
(
2
1
2
1
x
l
R
x
R
mg
R
R
Z (1) obliczamy R
1
i wstawiamy do (2)
(
)
( )
mg
l
F
mg
l
R
x
x
R
l
R
x
R
mgx
x
l
R
x
R
mg
R
mg
R
2
2
2
2
2
2
2
2
1
=
=
−
−
−
=
−
−
=
Mas belki obliczmy natychmiast z (1)
kg
200
10
800
1200
2
2
1
2
1
=
+
=
+
=
+
=
s
m
N
N
g
R
R
g
R
R
m
m
0,8
s
m
kg
2000
m
s
m
kg
1600
s
m
10
kg
200
m
2
N
800
2
2
2
=
⋅
=
⋅
⋅
=
=
mg
l
F
x
2
b) Niech o obrotu przechodzi przez lewy koniec belki. Wtedy
m
8
,
0
)
2
(
)
1
(
2
2
2
2
1
=
=
=
=
=
+
mg
l
F
mg
l
R
x
l
R
mgx
mg
R
R
c) Niech o obrotu przechodzi przez prawy koniec belki. Wtedy
( )
m
0,8
m
m
2000
2400
4000
s
m
10
kg
200
m
2
N
1200
m
2
s
m
10
kg
200
2
2
=
=
−
=
⋅
⋅
−
⋅
⋅
=
−
=
−
=
−
=
−
=
−
=
=
+
2000
1600
)
2
(
)
1
(
1
1
1
1
1
2
1
mg
l
F
mgl
mg
l
R
mgl
x
l
R
mgl
mgx
mgx
mgl
l
R
x
l
mg
l
R
mg
R
R
Q = mg
R
2
R
1
x
l
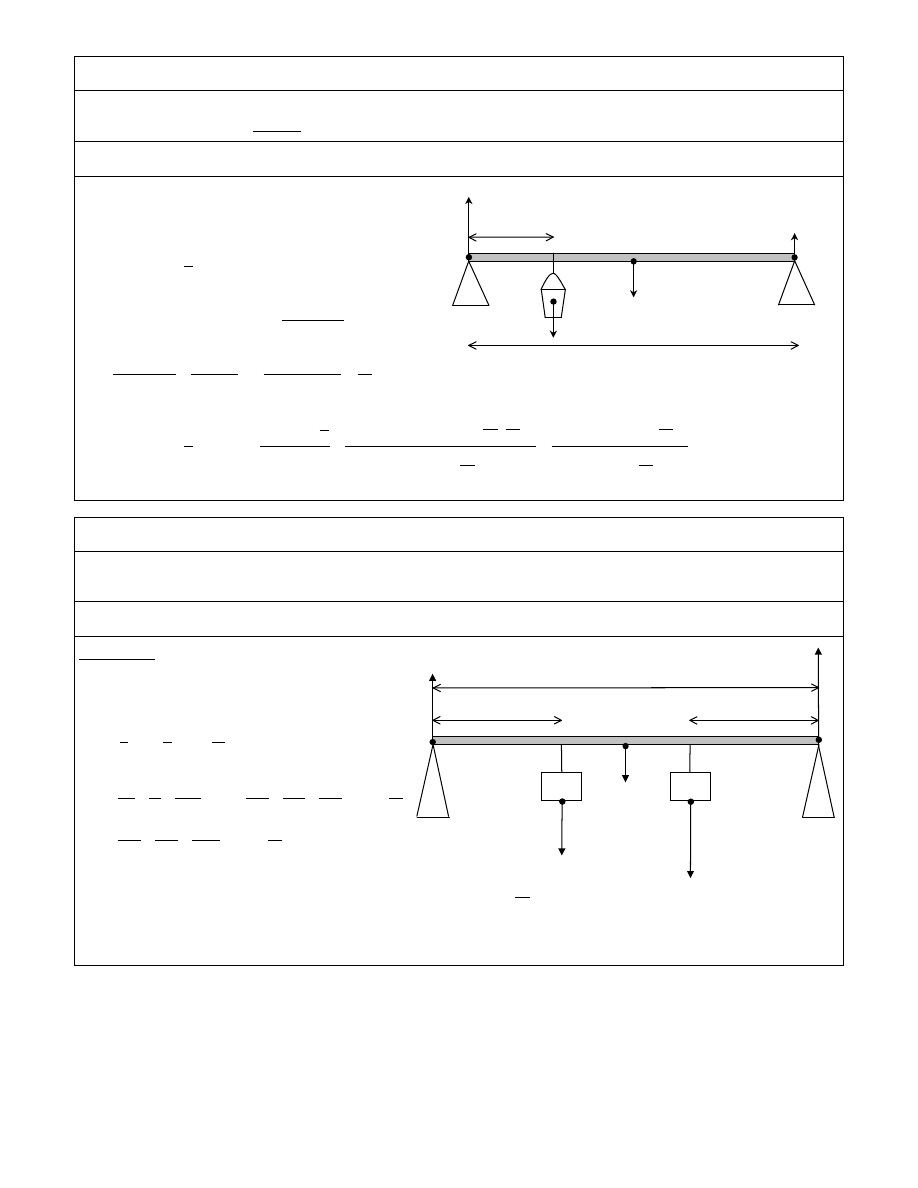
ZAD. 49
Belk o masie m
1
= 10 kg podparto na ko cach. W jakiej odległo ci od lewego ko ca nale y powiesi wiadro o masie m
2
= 40 kg, aby
obci enie lewej podpory było trzy razy wi ksze ni prawej. Odległo mi dzy podporami wynosiła l = 16 m.
Odp.: x = 1,125 m
Niech o obrotu przechodzi przez np. lewy koniec belki.
Wtedy
statyki)
Prawo
(II
statyki)
prawo
(I
2
1
2
2
1
l
g
m
gx
m
l
R
g
m
g
m
R
R
P
P
L
+
=
+
=
+
Mamy jednak warunek R
L
= 3R
P
. Zatem (I) mo emy zapisa
4
3
2
1
2
1
g
m
g
m
R
g
m
g
m
R
R
P
P
P
+
=
+
=
+
St d obliczamy R
P
N
s
m
10
4
kg
40
kg
10
2
125
4
4
2
1
2
1
=
+
=
+
=
+
=
g
m
m
g
m
g
m
R
P
Otrzymany wynik na R
p
wstawiamy do (II)
m
s
m
10
kg
40
m
s
m
kg
800
Nm
2
s
m
10
kg
40
m
2
16
s
m
10
kg
10
m
16
N
125
2
2
2
2
3
000
2
2
2
1
1
2
=
⋅
−
=
⋅
⋅
⋅
−
⋅
=
−
=
+
=
g
m
l
g
m
l
R
x
l
g
m
gx
m
l
R
p
P
ZAD. 50
Jednorodn szyn o masie m = 100 kg podparto na ko cach. W odległo ci 1/3 jej długo ci od lewego ko ca powieszono ci ar o
masie m
1
= 200 kg, a w odległo ci 1/3 od prawego ko ca drugi ci ar o masie m
2
= 300 kg. Jakie jest obci enie podpór?
Odp.: F
1
= 2833,3 N, F
2
= 3166,7 N,
Rozwi zanie:
Wybieramy o przechodz ca np. przez lewy koniec belki.
Wtedy
statyki)
prawo
(II
m
statyki)
prawo
(I
1
2
2
2
1
2
1
3
2
2
3
lR
l
g
m
l
mg
l
g
mg
g
m
g
m
R
R
=
+
+
+
+
=
+
Z (II) obliczamy R
2
N
s
m
10
kg
6
1200
6
300
6
400
s
m
10
kg
3
600
2
100
3
200
2
2
7
,
3166
3
2
2
3
2
1
2
=
⋅
+
+
=
=
⋅
+
+
=
⋅
+
+
=
g
m
m
m
R
Obliczone R
2
wstawiamy do (I)
(
)
(
)
(
)
N
R
g
m
m
m
R
mg
g
m
g
m
R
3
,
2833
6000
2
2
1
2
2
1
1
=
−
=
−
⋅
+
+
=
−
⋅
+
+
=
−
+
+
=
N
3166,7
N
3166,7
s
m
10
kg
100
300
200
2
Obci enia podpór s :
F
1
= R
1
= 2833,3 N,
F
2
= R
2
= 3166,7 N.
m
1
l/3
l/3
l
m
2
R
2
R
1
m
1
g
m
2
g
mg
R
L
= 3R
p
R
P
m
2
g
m
1
g
l
x
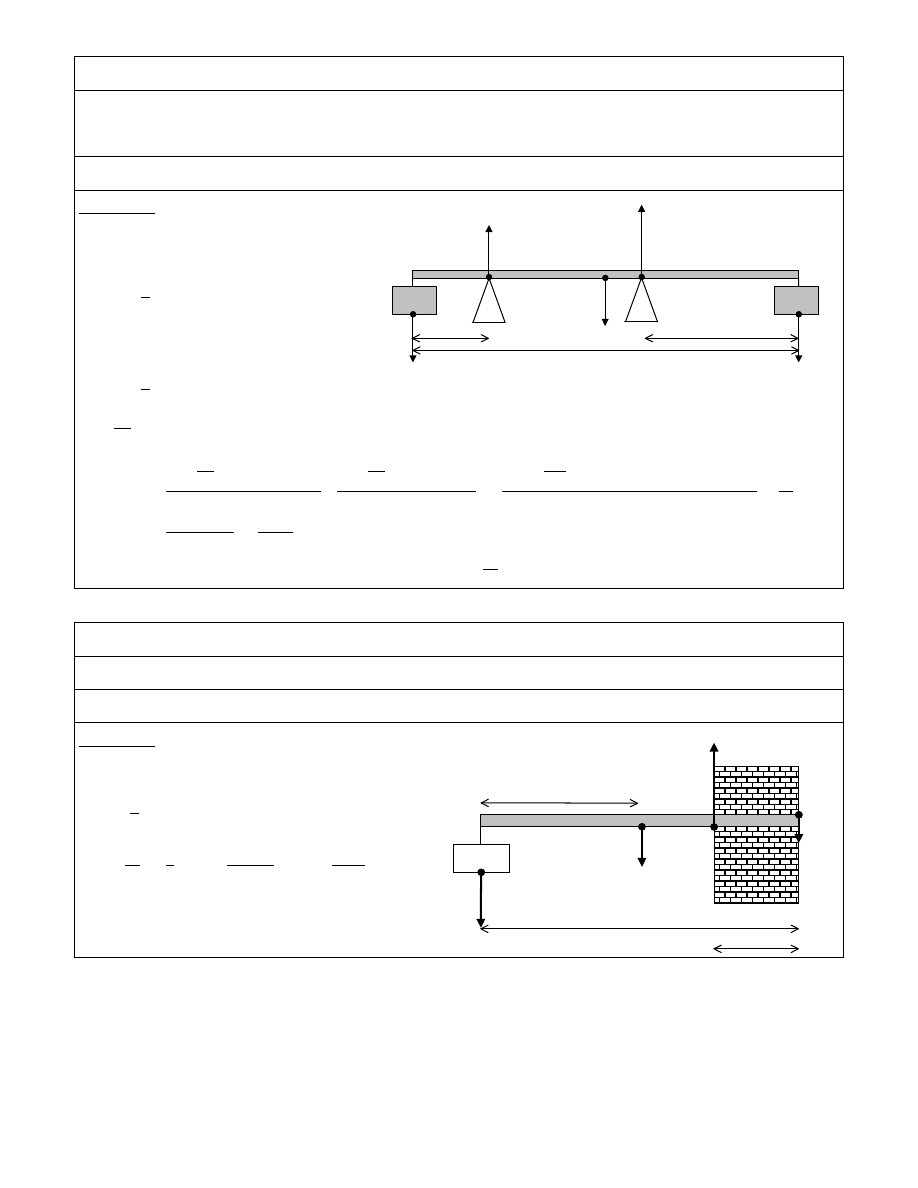
ZAD. 51
Stalowy, jednorodny pr t o masie m
1
= 100 kg i długo ci l = 5 m umieszczono na dwóch podporach. Lewa cz
pr ta wystawała
poza lew podpor na odległo l
L
= 1 m, a prawa poza praw podpor na odległo l
P
= 2 m? Do lewego i prawego ko ca
podwieszono dwa jednakowe ci ary o masie m = 200 kg. Oblicz obci enie ka dej z podpór.
Odp.: R
1
= 1250 N, R
2
= 3750 N
Rozwi zanie:
Wybieramy o przechodz ca np. przez prawy koniec belki.
Wtedy
(
)
statyki)
prawo
(II
statyki)
prawo
(I
P
L
l
R
l
l
R
l
g
m
mgl
mg
g
m
R
R
2
1
1
1
2
1
2
2
+
−
=
+
+
=
+
Z (I) obliczamy R
2
i wstawiamy do (II)
(
) (
)
(
)
(
)
(
)
(
)
(
)
(
)
N
1250
s
m
kg
10
2
1000
1250
s
m
10
m
2
1
5
m
2
kg
200
2
100
m
5
kg
2
100
200
2
2
=
⋅
⋅
−
=
=
⋅
−
−
⋅
⋅
+
−
⋅
+
=
−
−
+
−
+
=
−
−
+
−
+
=
+
+
−
−
=
+
−
+
+
−
=
+
−
+
=
g
l
l
l
l
m
m
l
m
m
l
l
l
gl
m
m
gl
m
m
R
gl
m
m
R
l
l
l
gl
m
m
l
R
mg
g
m
l
l
R
l
g
m
mgl
R
mg
g
m
R
P
L
P
P
L
P
P
P
L
P
L
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
(
)
(
)
N
3750
N
1250
s
m
10
kg
200
2
100
2
=
−
⋅
⋅
+
=
−
+
=
−
+
=
1
1
1
1
2
2
2
R
g
m
m
R
mg
g
m
R
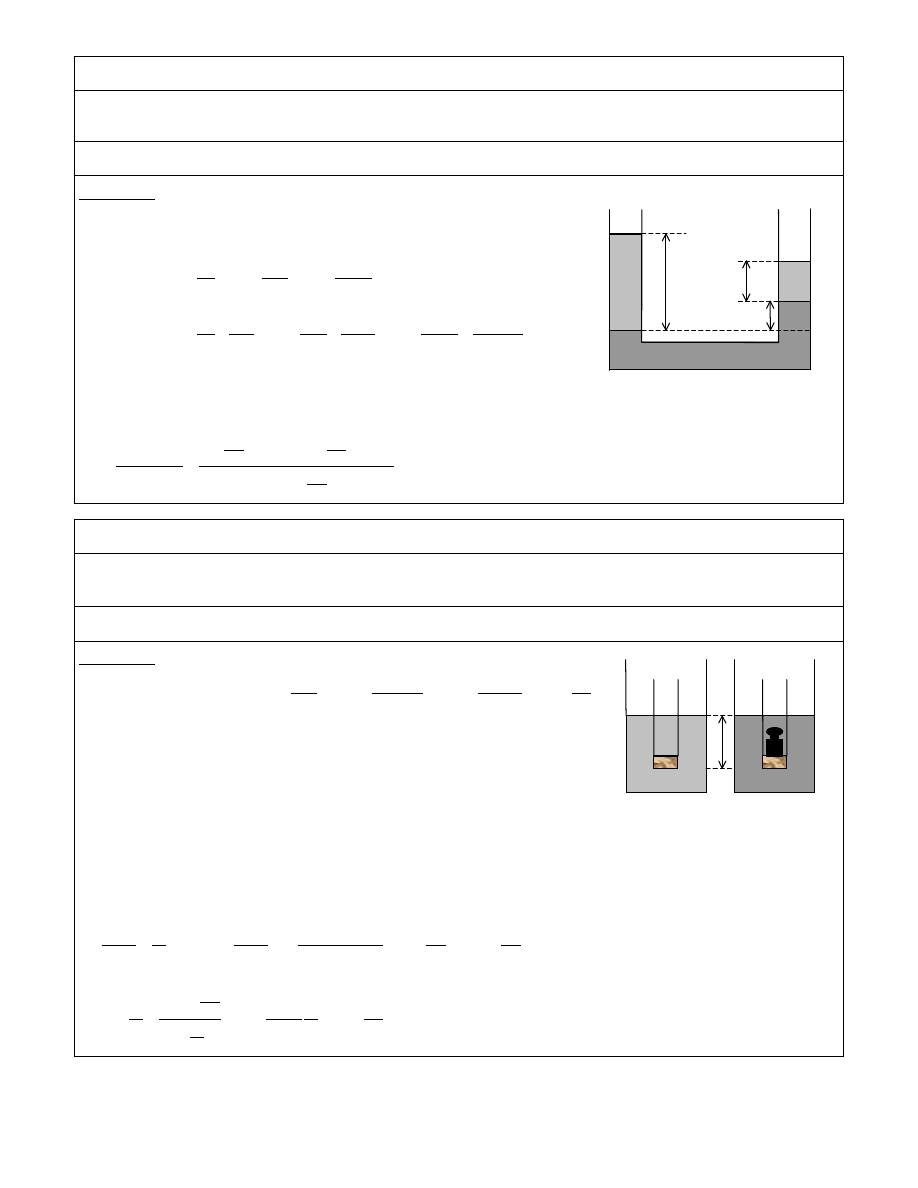
ZAD. 52
Jednorodna pozioma belka o długo ci l = 2 m i ci arze Q = 500 N ma jeden koniec wpuszczony w cian o grubo ci s = 50 cm.
Swobodny koniec belki obci ono ci arem P = 1000 N. Znale siły reakcji ciany w punktach A i B.
Rozwi zanie:
O obrotu wybieramy np. w punkcie B. Wtedy
statyki)
prawo
(II
statyki)
prawo
(I
Pl
l
Q
s
R
Q
P
R
R
A
B
A
+
=
+
+
=
2
Z (II) obliczamy R
A
N
m
N
m
m
N
s
l
P
s
l
Q
R
A
5000
5
,
0
2
1000
5
,
0
2
2
500
2
=
+
⋅
=
+
=
R
B
obliczamy wstawiaj c warto R
A
do (I)
N
3500
N
500
N
1000
N
5000
=
−
−
=
−
−
=
Q
P
R
R
A
B
P
A
R
A
R
B
B
l
l/2
s
Q
m
m
R
1
m
1
g
mg
mg
R
2
l
l
L
l
P
m
1

ZAD. 53
Zmieszano dwie idealne ciecze: wod o g sto ci
ρ
w
= 1 g/cm
3
oraz denaturat o g sto ci
ρ
d
= 900 kg/m
3
.
a) Oblicz g sto ρ
1
kulki,
która w mieszaninie cieczy powstałej ze zmieszania jednakowych obj to ci wody i denaturatu tonie si z przyspieszeniem
a
1
= 0,5 m/s
2
,
b) Znajd przyspieszenie a
2
z jakim ta kulka b dzie si porusza w mieszaninie powstałej ze zmieszania jednakowych
mas tych cieczy.
c) Jaka jest g sto ρ
2
innej kulki zanurzaj cej si w denaturacie do połowy?
Odp.:
Rozwi zanie:
(
)
3
3
6
3
3
2
3
m
kg
1000
m
10
kg
10
1
m
10
kg
10
1
=
⋅
=
⋅
=
=
ρ
−
−
−
−
3
1
cm
g
w
a) Nale y obliczy g sto cieczy powstałej ze zmieszania jednakowych obj to ci wody i denaturatu:
3
3
m
kg
950
m
kg
2
900
1000
mamy
e
j c,
uwzgl dnia
=
+
=
ρ
+
ρ
=
ρ
+
ρ
=
ρ
=
=
+
ρ
+
ρ
=
+
+
=
=
ρ
2
2
d
w
d
w
c
d
w
d
w
d
d
w
w
d
w
d
w
c
V
V
V
V
V
V
V
V
V
V
V
V
m
m
V
m
Kulka w mieszaninie o g sto ci
ρ tonie z przyspieszeniem a = 0,5 m/s
2
. Na kulk działaj dwie siły (opór lepko ci zaniedbujemy). S
to:
1. siła ci ko ci Q = mg =
ρ
1
V
k
g oraz
2. siła wyporu, która zgodnie z prawem Archimedesa równa jest ci arowi cieczy wypartej przez kulk F
w
= m
c
g =
ρ
c
V
k
g
I zasad dynamiki zapiszemy dla tego przypadku w postaci:
(
)
(
)
(
)
3
3
2
2
m
kg
1000
m
kg
950
s
m
0,5
10
s
m
10
=
⋅
−
=
ρ
⋅
−
=
ρ
ρ
⋅
−
=
−
ρ
=
ρ
ρ
=
−
ρ
ρ
−
ρ
=
ρ
−
=
c
c
k
k
c
k
c
k
k
c
k
k
w
a
g
g
a
g
g
a
g
V
g
V
g
V
a
g
V
g
V
g
V
a
V
F
Q
ma
1
1
1
1
1
1
1
1
1
1
1
b) Nale y wyznaczy g sto ρ
c2
cieczy powstałej ze zmieszania jednakowych mas wody i denaturatu
(
)
3
3
m
kg
m
kg
mamy
e
j c,
uwzgl dnia
4
,
947
900
1000
900
1000
2
2
2
2
2
2
=
+
⋅
⋅
=
ρ
+
ρ
ρ
ρ
=
ρ
ρ
+
ρ
ρ
ρ
=
ρ
ρ
⋅
ρ
+
ρ
+
=
ρ
=
=
ρ
ρ
⋅
ρ
+
ρ
+
=
ρ
+
ρ
+
=
+
+
=
=
ρ
w
d
d
w
c
w
d
d
w
d
w
w
d
c
d
w
d
w
w
d
d
w
d
w
d
d
w
w
d
w
d
w
d
w
c
m
m
m
m
m
m
m
m
m
m
m
m
m
m
V
V
m
m
V
m
Przyspieszenie a
2
obliczymy z równania
(
)
2
2
s
m
0,526
s
m
10
1000
947,4
1000
=
⋅
−
=
⋅
ρ
ρ
−
ρ
=
ρ
−
ρ
=
ρ
−
=
g
a
g
V
g
V
a
V
F
Q
ma
c
k
c
k
k
w
1
2
1
2
2
1
2
1
2
c) Kulka jest zanurzona do połowy w denaturacie. Na kulk działaj dwie siły; ci ar Q oraz siła wyporu F
w
.. Kulka jest nieruchoma,
wi c siły te musz si równowa y . Zapiszemy to:
3
m
kg
450
=
ρ
=
ρ
=
ρ
=
ρ
ρ
=
ρ
=
=
2
2
1
2
2
d
d
k
k
d
k
z
z
d
k
d
w
V
V
V
V
V
V
g
m
mg
F
Q
gdzie V
z
jest obj to ci zanurzonej cz ci kulki (z warunków zadania wynika, e V
z
= ½V
k
)
ZAD. 54
Do U-rurki nalano rt ci, a na jej powierzchni w jednym ramieniu wlano oliw o g sto ci
ρ
o
= 920 kg/m
3
, a drugim ramieniu naft o
g sto ci
ρ
n
= 800 kg/m
3
. Wysoko słupków oliwy i nafty wynosiła odpowiednio h
o
= 48 cm i h
n
= 20 cm. Obliczy ró nic
poziomów rt ci w obu rurkach.
Rozwi zanie:
Na poziomie O-O ci nienia s jednakowe. Wynika to z faktu, e poni ej tego poziomu
ciecz (czyli rt ) jest jednorodna.
Dla lewej cz ci U-rurki mamy
g
h
p
S
g
V
p
S
g
m
p
S
Q
p
p
o
o
at
o
o
at
o
at
o
at
O
O
ρ
+
=
ρ
+
=
+
=
+
=
−
Dla prawej cz ci U-rurki mamy
g
h
g
h
p
S
g
V
S
g
V
p
S
g
m
S
g
m
p
S
Q
S
Q
p
p
Hg
Hg
n
n
at
Hg
Hg
n
n
at
Hg
n
at
Hg
n
at
O
O
ρ
+
ρ
+
=
=
ρ
+
ρ
+
=
+
+
=
+
+
=
−
Z porównania
Hg
Hg
n
n
o
o
Hg
Hg
n
n
at
o
o
at
h
h
h
g
h
g
h
p
g
h
p
ρ
+
ρ
=
ρ
ρ
+
ρ
+
=
ρ
+
czyli
m
0,0207
m
kg
13600
m
0,20
m
kg
800
m
0,48
m
kg
920
3
3
3
=
⋅
−
⋅
=
ρ
ρ
−
ρ
=
Hg
n
n
o
o
Hg
h
h
h
ZAD. 55
Probówka ze rutem wa y P = 0,2 N i zanurza si w cieczy o ci arze wła ciwym
γ = 8⋅10
-3
N/cm
3
do pewnej gł boko ci. Po
wrzuceniu do próbówki ci arka Q = 0,05 N zanurza si ona do tej samej gł boko ci w innej cieczy. Obliczy ci ar wła ciwy
γ
1
i
g sto
ρ
1
tej cieczy.
Odp.: γγγγ
1
=10000 N/m
3
, ρρρρ
1
= 1000 kg/m
3
Rozwi zanie:
Przeliczanie jednostek:
(
)
3
3
3
6
3
3
2
3
3
3
m
N
10
8
m
10
N
10
8
m
10
N
10
8
cm
N
10
8
⋅
=
⋅
=
⋅
=
⋅
=
γ
−
−
−
−
−
W obu przypadkach probówka jest nieruchoma, zatem w obu przypadkach działaj ce na
ni siły: ci ko ci oraz wyporu musz si równowa y . Ponadto probówka jest zanurzona
do tej samej obj to ci, wi c obj to ci V wypartych cieczy b d te same (cho ró ne ci ary
tych cieczy).
Dla probówki zanurzonej w cieczy o ci arze wła ciwym
γ = 8⋅10
-3
N/cm
3
warunek
równowagi zapiszemy:
(1)
V
P
γ
=
gdzie V jest obj to ci zanurzonej cz ci probówki,
γ -ci arem wła ciwym cieczy
Dla probówki zanurzonej w cieczy o nieznanym ci arze wła ciwym γ
1
warunek
równowagi zapiszemy:
(2)
V
Q
P
1
γ
=
+
Dziel c stronami (2) przez (1) otrzymujemy:
3
3
3
m
N
m
N
10
8
0,05
N
N
0,2
000
10
05
,
0
1
1
=
⋅
⋅
+
=
γ
⋅
+
=
γ
γ
γ
=
+
P
Q
P
P
Q
P
g sto
ρ otrzymamy z zale no ci:
3
2
3
2
2
3
m
kg
000
m
s
m
s
m
kg
000
s
m
10
m
N
000
10
1
1
1
1
=
⋅
=
=
γ
=
ρ
g
O
O
ρ
o
ρ
Hg
h
Hg
h
n
h
o
ρ
n
h
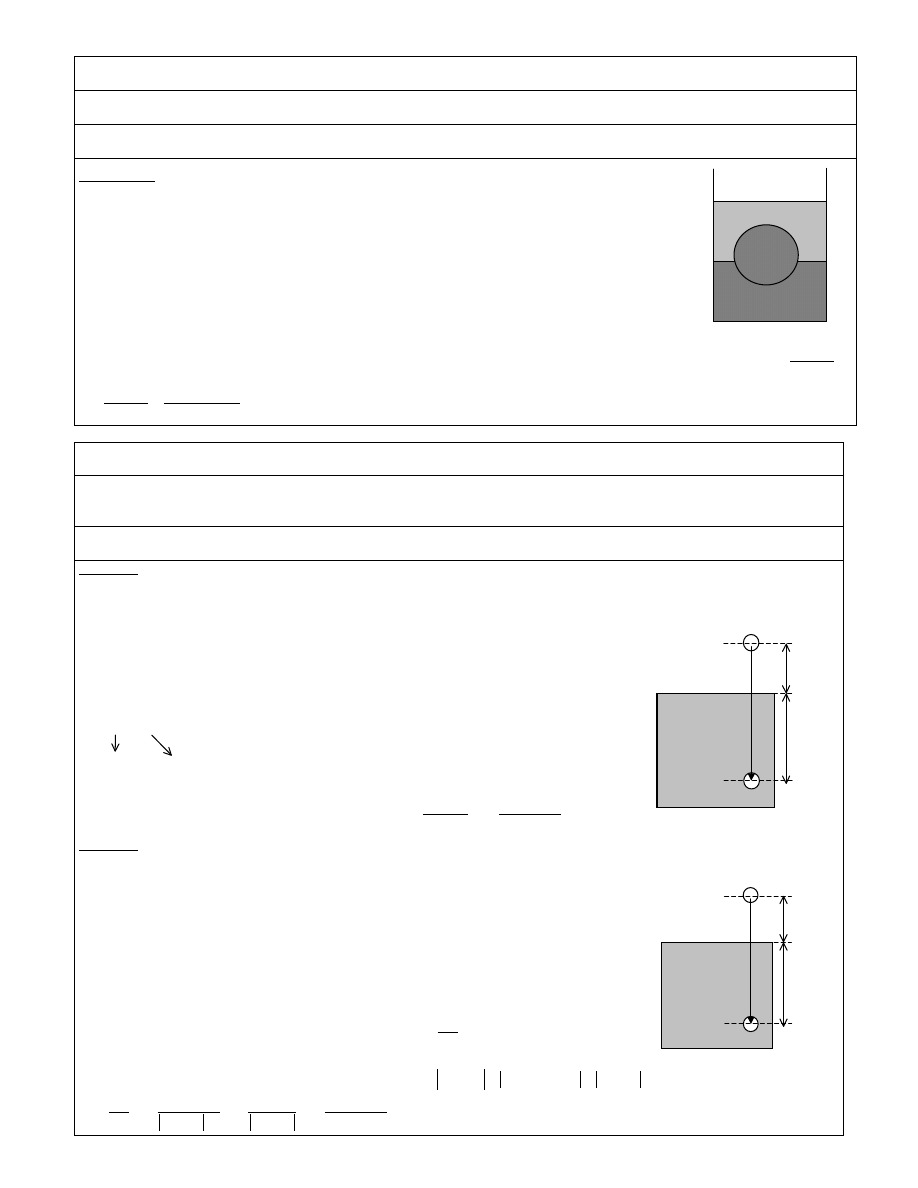
ZAD. 56
W naczyniu znajduje si rt i woda. Jaka cz
stalowej kulki wrzuconej do naczynia b dzie znajdowa si w wodzie? G sto wody
ρ
w
= 1000 kg/m
3
, rt ci
ρ
r
= 13600 kg/m
3
, stali
ρ
s
= 7700 kg/m
3
.
Odp.: V
w
/V
r
= 0,61
Rozwi zanie:
Na kulk działaj trzy siły: ci ar kulki
gV
Q
ρ
=
skierowany w dół oraz siły wyporu skierowane do góry.
Na siły wyporu składaj si : ci ar Q
w
wypartej wody oraz ci ar Q
r
wypartej rt ci
Ci ar wypartej rt ci ma warto
g
V
r
r
ρ
, gdzie V
r
jest cz ci obj to ci kulki, która jest zanurzona w rt ci.
Ci ar wypartej wody ma warto
g
V
r
r
ρ
, gdzie V
w
jest cz ci obj to ci kulki, która jest zanurzona w wodzie.
Kulka jest nieruchoma, wi c siły te musz si równowa y . Zapiszemy to:
w
w
r
r
s
w
w
r
r
s
r
w
V
V
V
g
V
g
V
Vg
Q
Q
Q
ρ
+
ρ
=
ρ
ρ
+
ρ
=
ρ
+
=
Oznaczmy przez k wielko poszukiwan w zadaniu, tj. k = V
w
/V
r
.
Wtedy, uwzgl dniaj c, e V
w
.= k
⋅ V
r.
oraz, e V = V
w
+ V
r
napiszemy:
(
)
47
,
0
1000
13600
7700
13600
=
−
−
=
ρ
−
ρ
ρ
−
ρ
=
ρ
−
ρ
ρ
−
ρ
=
ρ
+
ρ
=
ρ
+
ρ
ρ
+
ρ
=
ρ
+
ρ
ρ
+
ρ
=
+
ρ
ρ
+
ρ
=
ρ
w
s
r
s
w
s
r
s
w
r
s
s
r
w
r
r
t
s
r
s
w
w
r
r
w
r
s
w
w
r
r
s
k
k
k
k
kV
V
kV
V
V
V
V
V
V
V
V
ZAD. 57
Z wysoko ci h
1
= 10 m nad powierzchni wody i z zerow pr dko ci pocz tkow spada kulka o promieniu R = 5 cm wykonana z
materiału o g sto ci
ρ
k
= 600 kg/m
3
. Na jak maksymalna gł boko h
2
zanurzy si kulka? G sto wody
ρ
w
= 1000 kg/m
3
. Zadanie
rozwi za posługuj c si zasad zachowania energii i pracy. Zaniedba opór lepko ci.
Odp.: h
1
= 15 m
Wariant 1
Wykorzystanie zasady zachowania energii i pracy
Zmiana energii mechanicznej, czyli sumy energii kinetycznej i potencjalnej izolowanego układu ciał, jest równa wykonanej nad tym
układem pracy (dodatniej lub ujemnej).
Przed rozpocz ciem spadania kulka posiada energi kinetyczn E
k1
= 0 i energi potencjaln wzgl dem poziomu maksymalnego
zanurzenia kulki:
(
)
(
)
,
2
1
2
1
1
h
h
Vg
h
h
mg
E
k
P
+
ρ
=
+
=
gdzie V jest obj to ci kulki.
Na poziomie maksymalnego zanurzenia całkowita energia mechaniczne jest równa zeru (E
k2
= 0, E
P2
= 0).
Na cz ci drogi przebytej w wodzie na kulk działa siła wyporu F
w
= ρ
w
Vg, która wykonuje prac
2
2
gh
V
h
F
W
k
w
w
ρ
−
=
⋅
−
=
(znak minus gdy praca wykonana jest przeciw ruchowi).Poniewa
2
2
1
1
p
k
p
k
E
E
W
E
E
+
=
+
+
wi c
(
)
0
2
2
1
=
ρ
−
+
ρ
gh
V
h
h
g
V
k
w
k
k
Dziel c powy sze równanie obustronnie przez Vg otrzymujemy.
(
)
=
ρ
−
ρ
ρ
=
ρ
−
ρ
=
ρ
=
ρ
−
+
ρ
1
2
2
2
1
2
2
1
0
h
h
h
h
h
h
h
h
w
k
k
w
k
k
w
k
m
15
m
0
=
⋅
−
1
600
1000
600
Wariant 2
Zamiana energii potencjalnej pola grawitacyjnego w kinetyczn , nast pnie kinetycznej w potencjaln innego pola sił
W pierwszej fazie ruchu (w powietrzu) kulka porusza si polu w siły grawitacji. Energia potencjalna pola grawitacyjnego E
p
= mgh
1
zamienia si w energi kinetyczn E
k
= mv
2
/2, gdzie v jest pr dko ci kulki w chwili zderzenia z wod . Z zasady zachowania energii
kinetycznej i potencjalnej wynika, e
(1)
2
/
2
1
mv
mgh
=
W cieczy energia kinetyczna kulki zamienia si w energi potencjaln innego pola sił. Jest to pole
sił utworzone przez wypadkow siły wyporu i siły grawitacji. Kulka porusza si ruchem opó nio-
nym z opó nieniem a i jej energia kinetyczna przechodzi w energi potencjaln nowego pola sił.
W chwili zatrzymania energia potencjalna ma warto E
p
= mah
2
. Z zasady zachowania energii:
(2)
2
2
2
/
mah
mv
=
Z porównania (1) i (2) otrzymujemy:
1
2
2
1
h
ma
mg
h
mah
mgh
=
=
Pami taj c, e ma jest sił skierowan w gór , która opó nia ruch kulki w cieczy oraz, e warto tej siły jest warto ci bezwzgl dn
ró nicy siły ci ko ci oraz siły grawitacji mo na napisa :
gV
gV
gV
F
F
ma
k
w
k
w
g
w
ρ
−
ρ
=
ρ
−
ρ
=
−
=
m
15
m
0
=
⋅
−
=
ρ
−
ρ
ρ
=
ρ
−
ρ
ρ
=
=
1
600
1000
600
1
1
1
2
h
h
gv
gV
h
ma
mg
h
k
w
k
k
w
k
h
h
1
E
k2
= 0, E
P2
= 0
h
2
h
1
mah
2
mgh
1
mv
2
/2
V
w
V
r

Wyszukiwarka
Podobne podstrony:
HLP - oświecenie - opracowania lektur, 30. Jan Potocki, Rękopis znaleziony w Saragossie. DZIEŃ 43, 4
53 54 55
49,50,51
48 49 50 wielki format
50 51 52
48,49,46,51
Klaryski 49,50,51
54 55 56 folia PL
53 54
52 53
Jezyk polski 5 Ortografia Zas strony 48 49 id 222219
ei 01 2001 s 48 49
11 2003 51 52
więcej podobnych podstron