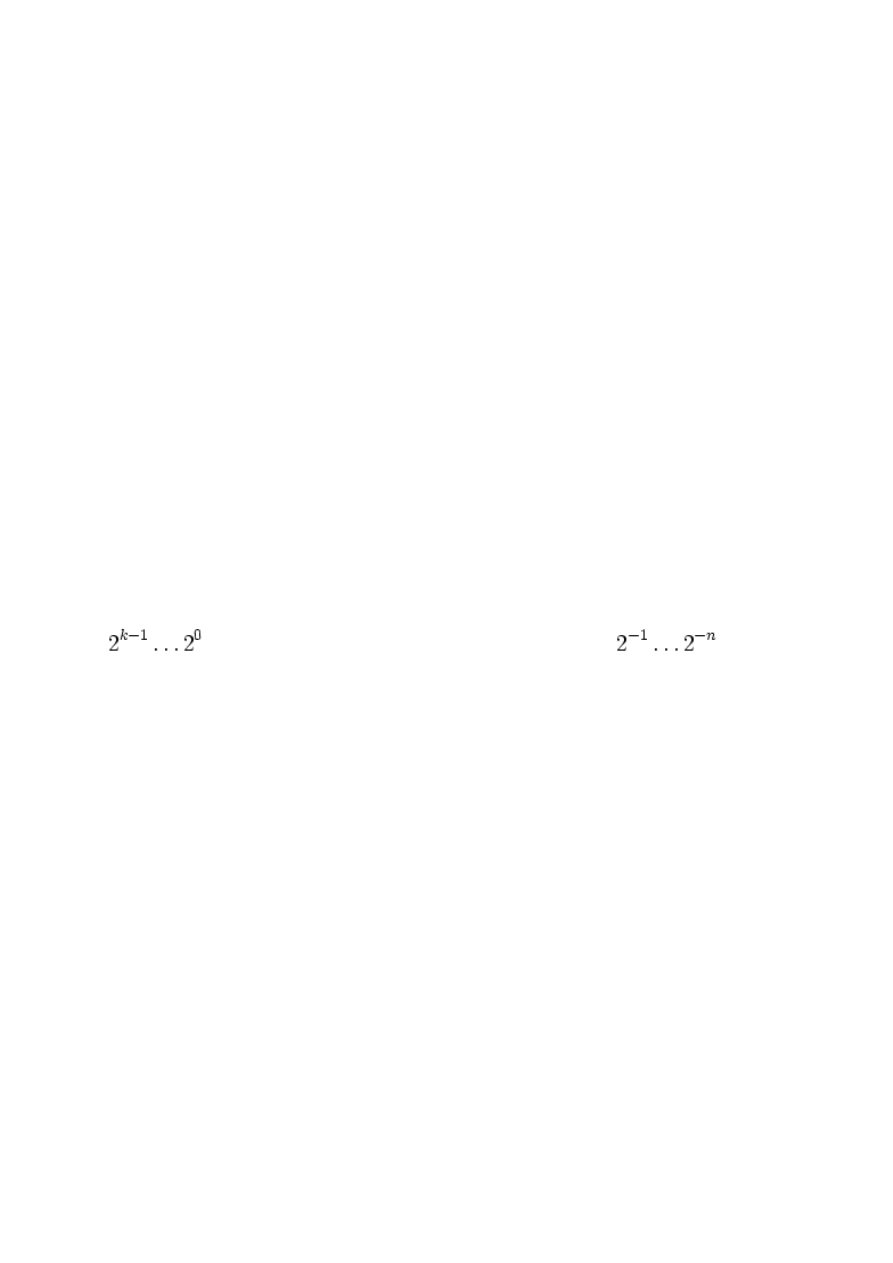
53. Arytmetyka stałopozycyjna i zmiennopozycyjna.

Zapis stałoprzecinkowy albo stałopozycyjny – jeden ze sposobów zapisu liczb ułamkowych
stosowanych w informatyce. Do zapisu liczby stałoprzecinkowej przeznaczona jest z góry
określona ilość cyfr dwójkowych, a pozycję przecinka ustala się arbitralnie, w zależności od
wymaganej dokładności.

Podziału na część całkowitą i ułamkową dokonuje projektant systemu lub programista, który
przewiduje z jak dużymi liczbami całkowitymi lub z jak dużą dokładnością obliczenia będą
wykonywane. Zwiększanie precyzji liczby to zmniejszanie zakresu, gdyż bity które mają
reprezentować część ułamkową (stać za przecinkiem) nie mogą już reprezentować wartości
całkowitych. Stwierdzenie odwrotne również jest prawdziwe: zwiększanie zakresu
(całkowitoliczbowego) to zmniejszanie precyzji (mniej bitów do dyspozycji na opisanie
części ułamkowej).

W skrajnych wypadkach możliwa jest sytuacja kiedy przecinek będzie stał poza znaczącymi
cyframi liczby. Jeśli będzie on z lewej strony, będziemy mieć zakres mniejszy od 1, jeśli z
prawej – precyzja będzie większa lub równa 1 (równość wystąpi, kiedy przecinek będzie stał
bezpośrednio za cyframi znaczącymi, będziemy mieć wtedy zwykłe liczby całkowite).

Zakresy liczb

Wartość liczby stałoprzecinkowej jest określana tak jak w pozycyjnym systemie dwójkowym.
Wagi bitów części całkowitej mają wartości (kolejno, od najbardziej znaczącego bitu):

, natomiast wagi bitów części ułamkowej mają wartości:

.

Dokładność reprezentacji wynosi 2

− n

, czyli jest równa wadze najmniej znaczącego bitu

części ułamkowej.

Na przykład jeśli na część całkowitą zostaną przeznaczone 4 bity (k = 4), natomiast na część
ułamkową 2 bity (n = 2), wówczas:

•

wartość maksymalna:

1111,11

2

= 2

3

+ 2

2

+ 2

1

+ 2

0

+ 2

-1

+ 2

-2

= 15,75

10

•

wartość minimalna:

0000,01

2

= 2

-2

= 0,25

10

•

przykładowa liczba:

1011,10

2

= 2

3

+ 2

1

+ 2

0

+ 2

-1

= 11,5

10

Zastosowania

Zapis stałoprzecinkowy ma tę zaletę, że arytmetyka stałoprzecinkowa może zostać
zrealizowana za pomocą działań całkowitoliczbowych. Dzięki temu działania na ułamkach są
do realizowania tam, gdzie nie ma możliwości użycia liczb zmiennoprzecinkowych: na
procesorach bez jednostki zmienoprzecinkowej, na prostych mikrokomputerach lub w

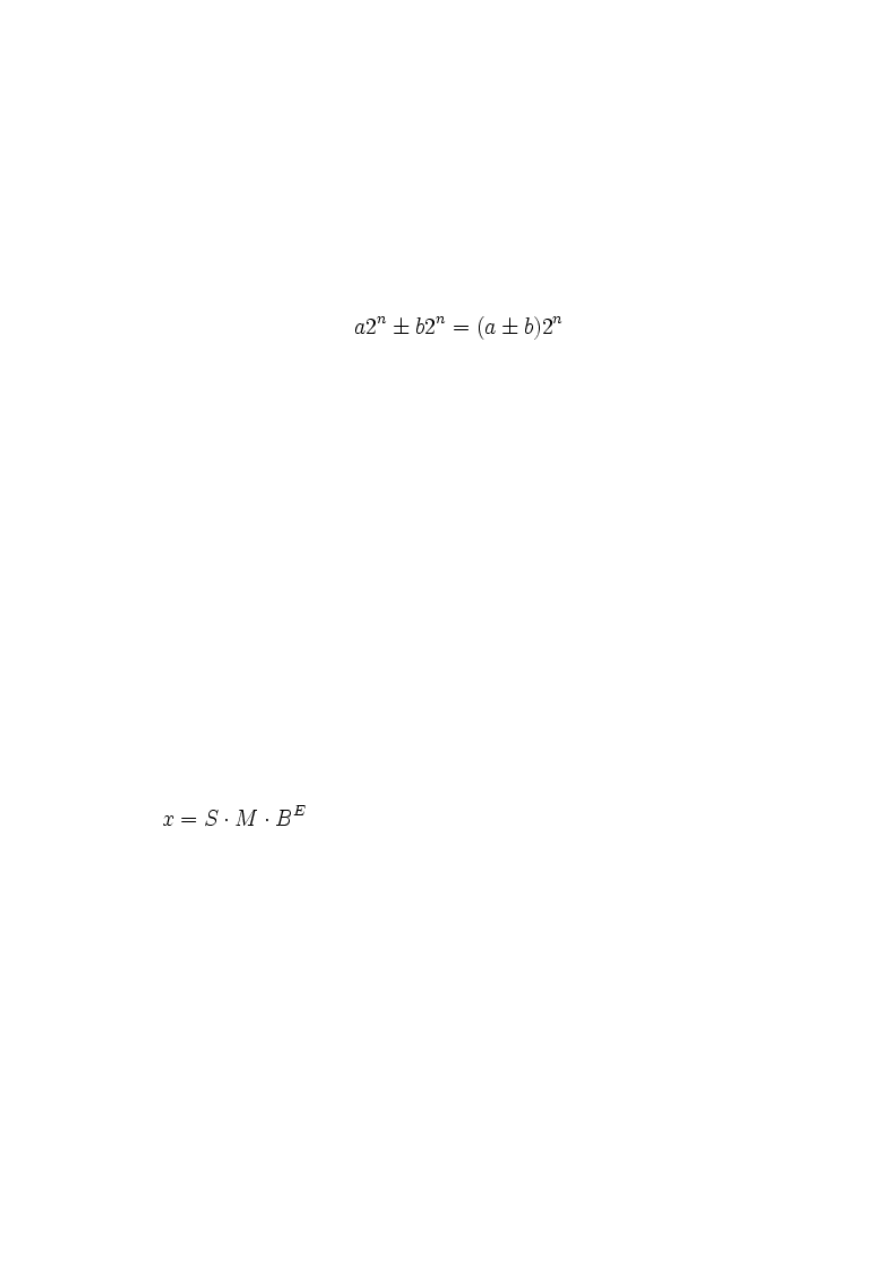
programach używających rozkazów MMX. Zapis stałoprzecinkowy był także powszechnie
stosowany gdy jednostka zmiennoprzecinkowa procesora była nie dość wydajna, a
jednocześnie nie była potrzebna wysoka dokładność obliczeń, np. w szybkich procedurach
graficznych.

Operacje na liczbach stałoprzecinkowych

Jeśli obliczyć wartość liczby stałoprzecinkowej x w naturalnym kodzie dwójkowym, wartość
ta wyniesie x2

n

. Wówczas działania całkowitoliczbowe mają postać:

•

Dodawanie/odejmowanie:

- wynik nie wymaga korekty,

jest to zapis stałoprzecinkowy z założoną dokładnością.

•

Mnożenie: a2

n

b2

n

= ab2

2n

- wynik wymaga korekty, należy podzielić go przez 2

n

, aby

uzyskać postać x2

n

.

•

Dzielenie całkowitoliczbowe. W tym przypadku dzielną a należy przemnożyć przez
czynnik 2

n

przed wykonaniem dzielenia i wówczas: a2

2n

/ b2

n

= (a / b)2

n

.

Mnożenie i dzielenie przez potęgę dwójki, w tym przypadku 2

n

, jest równoważne

przesunięciu bitowemu (odpowiednio) w lewo bądź prawo o n bitów; jest to operacja bardzo
szybka.

Zapis zmiennoprzecinkowy

Liczba zmiennoprzecinkowa – komputerowa reprezentacja liczb rzeczywistych zapisanych
w postaci wykładniczej (zwanej też notacją naukową). Ze względu na wygodę operowania na
takich liczbach przyjmuje się ograniczony zakres na mantysę i cechę. Powoduje to, że
reprezentacja jest tylko przybliżona a jedna liczba zmiennoprzecinkowa może reprezentować
różne liczby rzeczywiste z pewnego odcinka.

Wartość liczby zmiennoprzecinkowej jest obliczana wg wzoru:

gdzie:

•

S (sign) – znak liczby, 1 lub -1

•

M (mantissa) – znormalizowana mantysa, liczba ułamkowa

•

B (base) – podstawa systemu liczbowego (2 dla systemów komputerowych)

•

E (exponent) – wykładnik, liczba całkowita

Mantysa jest znormalizowana, tj. należy do przedziału [1,B) (przedział prawostronnie
otwarty!). Jeżeli M jest stałe, a E zmienia się, wówczas przesunięciu ulega przecinek – stąd
właśnie pochodzi nazwa tej reprezentacji.

Zarówno dla mantysy jak i wykładnika ilość cyfr jest z góry ustalona. Zatem dana liczba jest
reprezentowana z pewną skończoną dokładnością i należy do skończonego zbioru wartości.

Załóżmy, że m to liczba cyfr przeznaczonych na mantysę, natomiast n+1 to liczba cyfr
przeznaczonych na wykładnik (n cyfr dla wartości i 1 dla znaku wykładnika). Uznaje się
również, że jedna dodatkowa pozycja (najstarsza) zarezerwowana jest dla zapisu znaku całej
liczby. Wówczas wartości maksymalne i minimalne dla M i E określone są następująco:

•

Wykładnik E:

o

E

min

= − B

n

+ 1

o

E

max

= B

n

− 1

•

Mantysa M:

o

M

min

= 1

o

M

max

= B − B

− (m − 1)

Stąd najmniejsza i największa liczba dodatnia możliwa do zapisania w takiej reprezentacji to:

•

•

.

Zakres liczb, które mogą być reprezentowane w danym zapisie wynosi:

Zero jest wartością specjalną, która nie może zostać bezpośrednio reprezentowana w tym
formacie.

Błąd względny reprezentacji wynosi

(inaczej: waga najmniej znaczącej cyfry

mantysy). Błędów bezwzględnych na ogół się nie podaje.

Jeżeli komputer wygeneruje liczbę

, to traktowana jest jako niedomiar

(underflow).

W przypadku, gdy otrzymana liczba

, to traktowana jest jako

nadmiar wykładniczy (overflow).

Przykład reprezentacji

Przyjmijmy, że B = 10, liczba cyfr dziesiętnych przeznaczonych na mantysę wynosi 4,
natomiast na wykładnik 2. Chcemy zapisać wartość 60,89523.

1. Pierwszy etap to normalizacja mantysy, sytuacja przedstawia się następująco:

. Mantysa M nie należy do zadanego przedziału [1,10),

zatem należy przesuwać przecinek w lewo do chwili, aż wartość M będzie doń
należała. Przesuwanie przecinka w lewo wiąże się ze zwiększaniem E.

2. Po normalizacji (przesunięciu przecinka o 1 pozycje w lewo) otrzymujemy:

3. Ostatnim krokiem jest odpowiednie obcięcie (ang. truncate), albo zaokrąglenie (ang.

round) mantysy do zadanej ilości cyfr.

o

obcięcie:

o

zaokrąglenie:

Przykład dla liczby mniejszej od 1: 0,0000125.

1. Mantysa 0,0000125 nie jest znormalizowana, należy tym razem przesuwać przecinek

w prawo, co wiąże się ze zmniejszaniem E.

2. Po normalizacji, tj. przesunięciu przecinka o 5 pozycje w prawo, otrzymujemy:

.

3. Liczba cyfr znaczących jest mniejsza od dostępnej, więc nie potrzebna żadna forma

zaokrąglania. Liczba ma postać

.

Operacje na liczbach zmiennoprzecinkowych

Własności arytmetyki zmiennoprzecinkowej

Arytmetyka zmiennoprzecinkowa nie jest łączna. To znaczy: iż dla x, y i z mogą zachodzić
różności:

•
•

,

ani rozdzielna czyli może zachodzić różność:

•

Innymi słowy kolejność wykonywania operacji wpływa na końcowy wynik.

Przy obliczeniach zmiennoprzecinkowych występują też inne problemy:

•

zaokrąglenia

•

nieprawidłowe operacje

•

przepełnienie

•

niedomiar

Dodawanie i odejmowanie

Załóżmy że chcemy dodać lub odjąć dwie dodatnie liczby zmiennoprzecinkowe:

oraz

, przy czym

. Założenia te można spełnić

dla dowolnych liczb zmiennoprzecinkowych manipulując ich kolejnością, znakiem wyniku
oraz rodzajem wykonywanej operacji, wg poniższego schematu:

Wówczas:

Jeśli liczby mają różne wykładniki, to podczas dodawania mantysa liczby o mniejszym
wykładniku musi zostać zdenormalizowana – we wzorze jest to przemnożenie M

2

przez

czynnik

. W szczególnym przypadku, jeśli E

1

− E

2

jest większe niż m (ilość cyfr

mantysy), to po tej denormalizacji mantysa będzie miała wartość 0 i liczba o mniejszym
wykładniku nie wpłynie na wynik dodawania bądź odejmowania.

Odejmowanie liczb zmiennoprzecinkowych o takim samym wykładniku E i niewiele
różniącej się mantysie, powoduje że wynikowa mantysa jest znacznie zdenormalizowana.
Renormalizacja w takim wypadku wiąże się z wprowadzeniem sporej ilości nieznaczących
zer na końcu mantysy. Jest to szczególnie niekorzystne, dlatego zwykle tak projektuje się
obliczenia aby do tego nie dopuścić.

Mnożenie i dzielenie

Mając dane liczby zmiennoprzecinkowe

i

:

54: Iteracja i rekurencja

Iteracja – czynność powtarzania (najczęściej wielokrotnego) tej samej instrukcji (albo wielu
instrukcji) w pętli. Mianem iteracji określa się także operacje wykonywane wewnątrz takiej
pętli.

Czynność iteracji przedstawia pętla, zapisana w poniższym pseudokodzie:

i=0
dopóki i<10 wykonuj

i=i+1
przeskocz do góry

W pierwszej iteracji otrzymamy wartość i=1, w następnej i=2, potem i=3 i tak dalej, a
iteracją jest powtarzana tu czynność, czyli zwiększanie zmiennej i o jeden (inkrementacja).

Kod w C/C++:

int i=0;

while (i<10) {
i++;

}

Kod w Pythonie:

i = 0
while i<10:

i += 1

Kod w Javie, za pomocą pętli for:

for(int i=0; i<10; i++){}

Kod w Scheme, funkcyjnym języku programowania:

;; sum : number -> number
;; to sum the first n natural numbers

(define (sum n)
(if (and (integer? n) (> n 0))

(let iter ([n n] [i 1])
(if (= n 1)

i
(iter (- n 1) (+ n i))))

((assertion-violation
'sum "invalid argument" n))))

Rekurencja albo rekursja (recursion) to w logice, programowaniu i w matematyce
odwoływanie się np. funkcji lub definicji do samej siebie. Przykład zastosowania rekurencji w
matematyce: definicja ciągu Fibonacciego

, dla

Jest ona rekurencyjna, gdyż definiuje funkcję odwołując się w definicji do niej samej.

Każda definicja rekurencyjna potrzebuje przynajmniej jednego przypadku bazowego (nie
rekurencyjnego), w tym przypadku są to wartości dla 0 i 1. W przeciwnym wypadku nigdy się
nie zakończy.

Dla przykładu, obliczenie

wygląda następująco:

Rekurencja w programowaniu:

Rekurencja jest podstawową techniką wykorzystywaną w funkcyjnych językach
programowania. Należy jednak zachować ostrożność przy używaniu rekurencji w

rzeczywistych programach. Ryzyko istnieje szczególnie przy przetwarzaniu dużej ilości
głęboko zagnieżdżonych danych.

Jeśli program nie jest w rzeczywistości rekurencyjny, to rekurencja może dramatycznie
zwiększyć złożoność obliczeniową. Ponadto rekurencja zawsze zwiększa pamięciowe
zapotrzebowanie programu (chyba że zostanie użyta możliwa w pewnych przypadkach
optymalizacja zwana rekursją ogonową), gdyż wymaga ona zapamiętania m.in. adresów
powrotu, pozwalających programowi "zorientować się" do którego miejsca ma wrócić po
zakończeniu jednego z wywołań rekurencyjnych. Inną częstą wadą rekurencji jest kompletnie
niezależne rozwiązywanie podproblemów, tak, że czasem jeden problem jest rozwiązywany
w kilku miejscach rozwinięcia rekurencji, np. w powyższym przykładzie obliczania
niepotrzebnie jest dwukrotnie obliczana wartość

(porównaj: programowanie

dynamiczne). Takie problemy nie pojawiają się przy drugim z przykładów. Niezaprzeczalną
zaletą rekurencji jest przejrzystość programów, które z niej korzystają.

Jedną z typowych sytuacji, w których stosuje się rekurencję jest przeszukiwanie danych o
strukturze nieregularnego drzewa, np. XML. Funkcja, która sprawdza czy w danym obiekcie
XML istnieje element o określonej zawartości mogłaby wyglądać następująco (tutaj w PHP
przy użyciu klasy SimpleXML):

function find_text($text, $tree) {

// sprawdź zawartość aktualnego elementu
if ($text == (string)$tree) {
return true;
}

// sprawdź wszystkie jego dzieci
foreach ($tree as $node) {

// tutaj następuje wywołanie rekurencyjne
if (find_text($text, $node)) {
return true;
}

}

// nic nie znaleziono
return false;}

Inny przykład – funkcja obliczająca silnię:

unsigned int silnia(unsigned int n)

{

if (n <= 1) {
return 1;

} else {
return n * silnia(n-1);

}
}

55: Instrukcje warunkowe i pętle

Instrukcja warunkowa jest w inżynierii oprogramowania jednym ze sposobów na
organizację kodu i kontrolowania programu. Procesor sprawdza czy warunek znajdująca się
wewnątrz if jest spełniony (ma wartość logiczną 1). Jeżeli się zgadza to program wykonuje
blok kodu zawarty po instrukcji if. W przeciwnym wypadku opuszcza go i przechodzi do
wykonywania kodu znajdującego się za nim. Istnieją różne typy instrukcji warunkowych:

If

if (warunek) then
{instrukcja jeśli warunek został spełniony}

If-then-else

if (warunek) then
(instrukcja jeśli warunek został spełniony)

Else
(instrukcja gdy warunek nie został spełniony)

End If

Else-if

if warunek then

{instrukcja jeśli warunek został spełniony}
elsif warunek2 then

{instrukcja jeśli warunek2 został spełniony}
elsif warunek3 then

{instrukcja jeśli warunek został spełniony}
else warunek then

{instrukcja jeśli żaden z powyższych warunków nie został spełniony}
end if;

Instrukcja warunkowa jako operator

(warunek)?(instrukcja jeśli warunek został spełniony):(instrukcja jeśli
warunek nie został spełniony)

Tego typu operatory występują w językach o składni typowej dla języka C.

Instrukcja warunkowa w Haskellu

if' :: Bool -> a -> a -> a

if' True x _ = x
if' False _ y = y

Arytmetyczna instrukcja warunkowa (na przykładzie Fortrana)

IF (e) label1, label2, label3

Powyższy kod można zapisać w C++ w ten sposób:

if (e < 0) goto label1

if (e == 0) goto label2
if (e > 0) goto label3

Instrukcja warunkowa w SmallTalku:

var := warunek
ifTrue: [ 'foo' ]

ifFalse: [ 'bar' ]

Instrukcje Case i Switch

Instrukcje case i switch pozwalają na zapisanie skomplikowanej sekwencji warunków w
przystępny sposób. Można je również zapisać za pomocą kombinacji prostych operatorów if,
then i else.

W Pascalu:

case zmienna of

'a': instrukcje wykonane gdy zmienna = a;
'x': instrukcje wykonane gdy zmienna = x;

'y','z': instrukcje wykonane gdy zmienna = y lub zmienna = x;
else instrukcje do wykonania gdy zmienna nie przyjmuje żadnych z

powyższych wartości;
end;

W C/C++:

switch (zmienna) {
case 'a': {instrukcje wykonane gdy zmienna = a;} break;

case 'x': {instrukcje wykonane gdy zmienna = x;} break;
case 'y':

case 'z': {instrukcje wykonane gdy zmienna = y lub zmienna = x;} break;
default: {instrukcje do wykonania gdy zmienna nie przyjmuje żadnych z

powyższych wartości};
;

}

Pętla to jedna z trzech podstawowych konstrukcji programowania strukturalnego (obok
instrukcji warunkowej i instrukcji wyboru). Umożliwia cykliczne wykonywanie ciągu
instrukcji określoną liczbę razy, do momentu zajścia pewnych warunków, dla każdego
elementu kolekcji lub w nieskończoność.

Pętla for:

for (ilośc wykonań) wykonaj (instrukcje).

Przykłady:

Pascal:

var counter: integer;

begin
for counter:=1 to 10 do

WriteLn('Linia numer ', counter);
end.

C++:

for (int i=0; i<10; ++i)
std::cout << i << "-ta iteracja." << std::endl;

PHP:

for ($i=0 ; $i<10 ; ++$i)
echo $i . "-ta iteracja.<br />";

JavaScript:

var i;

for (i=0 ; i<10 ; ++i)
document.write(i + "-ta iteracja.<br />");

Python:

for i in range(1, 10):
print(i, '. iteracja', sep='')

Pętla while:

while ( warunek ) wykonuj (instrukcje)

C++:

unsigned int counter = 5;
unsigned long factorial = 1;

while (counter > 0)

{
factorial *= counter--; /* Multiply and decrement */

}

printf("%lu", factorial);

Java:

int counter = 5;

long factorial = 1;

while (counter > 1)
{

factorial *= counter--;
}

JavaScript:

var counter = 5;
var factorial = 1;

while ( --counter > 1 )

{
factorial *= counter;

}

document.body.appendChild(document.createTextNode(factorial));

LUA:

counter = 5

factorial = 1

while counter > 0 do
factorial = factorial * counter

counter = counter - 1
end

print(factorial)

Pascal:

program Factorial1;
var

Counter, Factorial: integer;
begin

Counter := 5;
Factorial := 1;

while Counter > 0 do
begin

Factorial := Factorial * Counter;
Counter := Counter - 1

end;
WriteLn(Factorial)

end.

Perl:

$factorial *= $counter-- while $counter > 0;

Pętla do-while:

do (instrukcje) while (warunek)

Tego typu pętla działa bardzo podobnie do klasycznych pętli while z tą różnicą, że warunek
jest sprawdzany już po wykonaniu instrukcji, toteż mamy gwarancję że zostaną one
wykonane co najmniej raz.

Java:

unsigned int counter = 5;
unsigned long factorial = 1;

do {
factorial *= counter--; /* Multiply, then decrement. */

} while (counter > 0);
printf("%lu\n", factorial);

C/C++:

unsigned int counter = 5;
unsigned long factorial = 1;

do {
factorial *= counter--; /* Multiply, then decrement. */

} while (counter > 0);
printf("%lu\n", factorial);

JavaScript:

var counter = 5;
var factorial = 1;

do {
factorial *= counter--; /* Multiply, then decrement. */

} while (counter > 0);
document.body.appendChild(document.createTextNode(factorial));

Pascal:

program Factorial;
var

Counter, Factorial: integer;
begin

Counter := 5;
Factorial := 1;

repeat

Factorial := Factorial * Counter;
Dec(Counter);

until Counter = 0;

WriteLn(Factorial);
end.

PHP:

<?php
$counter = 5;

$factorial = 1;
do {

$factorial *= $counter--;
} while ($counter > 0);

echo $factorial;
?>

Foreach

foreach (obiekt): (wykonaj instrukcje)

Pętle foreach wykonują instrukcję dla każdego obiektu z tablicy która została przekazana jako
argument.

Przykłady:

C/C++:

Te języki nie posiadają odpowiednika pętli foreach.

C#:

foreach (type item in set)
{

// do something to item
}

Delphi:

for enumerator in collection do

begin
//do something here

end;

Java:

for (type item: set) {

// do something to item
}

JavaScript:

for (var strProperty in objObject) {
if(objObject.hasOwnProperty(strProperty )) {

/*
do something to:

objObject [strProperty]
*/

}
}

PHP:

foreach ($set as $key => $value) {
echo "{$key} has a value of {$value}";

}