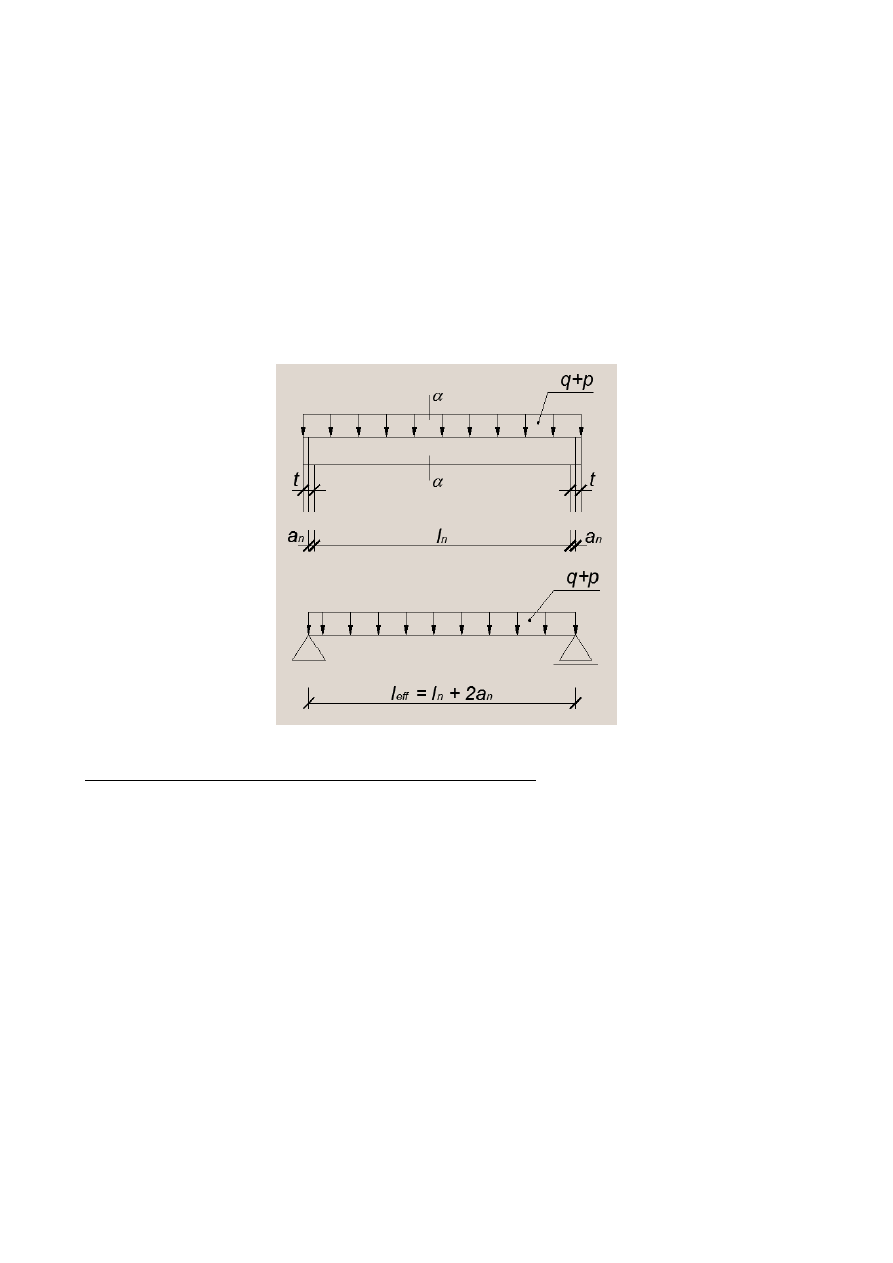
Przykład:

Zaprojektować zbrojenie w belce prefabrykowanej z uwagi na zginanie i ścinanie

w postaci strzemion pionowych. Sprawdzić stan graniczny użytkowania. Belka

pracuje w schemacie swobodnie podpartym, rozpiętość w świetle ścian

L

n

=5,62 m . Oparta jest na ścianie grubości

t

=0,38 m

. W obliczeniach przyjąć

beton klasy C16/20, stal zbrojenia podłużnego A-III, stal zbrojenia poprzecznego A-I.

Belka przeznaczona do pracy w klasie ekspozycji XC2.

Rysunek 1: Schemat statyczny belki

Parametry wytrzymałościowe przyjętych materiałów:

Beton C16/20

f

ck

=16,0 MPa

,

f

cd

=10,6 MPa

,

f

ctm

=1,9 MPa

,

f

ctd

=0,87 MPa

,

f

cm

= f

ck

8=168=24 MPa

,

E

cm

=29 GPa

Stal A-III (34GS)

f

yk

=410 MPa , f

yd

=350 MPa , 

eff , lim

=0,53 , E

s

=200 GPa

Stal A-I (St3SX-b)

f

ykw

=240 MPa

,

f

ydw

=210 MPa

Zestawienie obciążeń:

Tabela 1: Zestawienie obciążeń zewnętrznych belki

Typ obciążenia

Wartość

charakterystyczna

[kN/m]

Współczynnik

obciążenia

Wartość

obliczeniowa

[kN/m]

Stałe:

22

1,18

25,96

Zmienne:

15

1,2

18

Razem:

37

43,96

Określenie rozpiętości efektywnej

a

n

=0,5 t=0,5⋅0,38=0,19 m

L

eff

= L

n

2 a

n

=5,622⋅0,19=6,0 m

Oszacowanie przekroju poprzecznego belki

Wysokość przekroju

h

=

1

15

÷

1
9

 L

eff

=

1

15

÷

1
9

6,0=0,4÷0,667  m

Przyjęto:

h

=0,6 m

Szerokość przekroju

b

=

1
3

÷

1
2

 h=

1
3

÷

1
2

0,6=0,198÷0,3m

Przyjęto:

b

=0,3 m

Ciężar własny belki:



b

=25,0

kN

m

3

Wartość charakterystyczna:

g

k

=

b

b h

=25,0⋅0,3⋅0,6=4,5

kN

m

.

Wartość obliczeniowa:

g

o

=1,1 g

k

=1,1⋅4,5=4,95

kN

m

.

Sumaryczne obciążenie belki

Tabela 2: Sumaryczne obciążenie belki

Typ obciążenia

Wartość

charakterystyczna

[kN/m]

Współczynnik

obciążenia

Wartość

obliczeniowa

[kN/m]

Stałe:

22

1,18

25,96

Ciężar własny

4,5

1,1

4,95

Sumarycznie stałe

26,5

30,91

Zmienne

15

1,2

18

RAZEM:

41,5

48,91

Maksymalne siły wewnętrzne w belce

Wartości charakterystyczne:

M

Sd , k

=

q

k

L

eff

2

8

=

41,5

⋅6,0

2

8

=186,75 kNm

V

Sd , k

=

q

k

L

eff

2

=

41,5

⋅6,0

2

=124,5 kN

Wartości obliczeniowe:

M

Sd

=

q

o

L

eff

2

8

=

48,91

⋅6,0

2

8

=220,1 kNm

V

Sd , max

=

q

o

L

eff

2

=

48,91

⋅6,0

2

=146,73 kN

Wymiarowanie zbrojenia podłużnego

Założenia:

średnica zbrojenia głównego

=20 mm

średnica strzemion



s

=6 mm

maksymalna średnica ziaren kruszywa

d

g

=16 mm

Grubość otuliny prętów

c

min

=25 mm (klasa ekspozycji XC2)

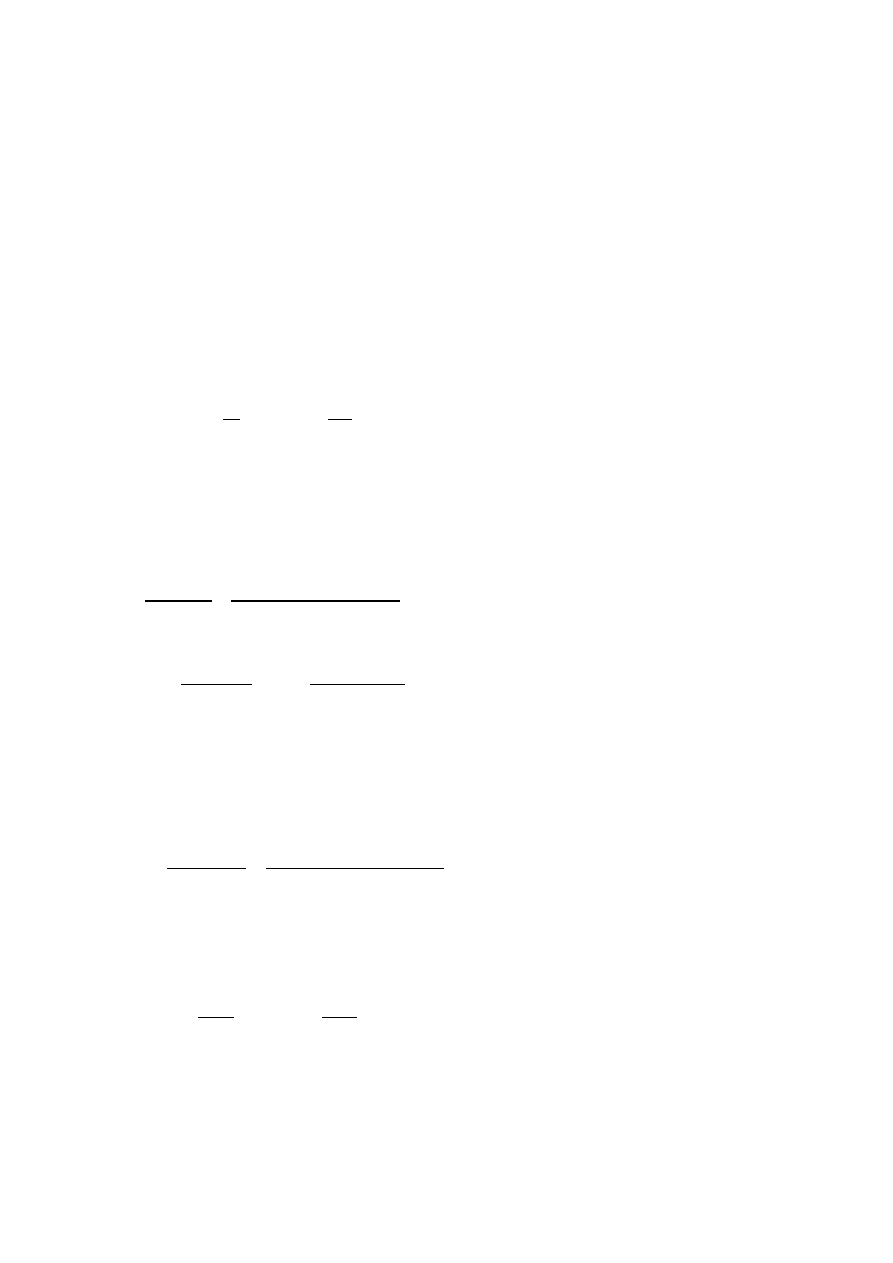
c

min

==20 mm

Odchyłka wymiarowa

c=5 mm

Nominalna grubość otuliny

c

nom

=c

min

 c=255=30 mm

Minimalne odległości w świetle prętów

s

1

=20 mm

,

s

1

==20 mm

,

s

1

=d

g

5=16 5=21 mm

Przyjęto:

s

1

=25 mm

Założono ułożenie zbrojenia podłużnego w jednej warstwie.

a

1

=c

nom



s





2

=306 

20

2

=46 mm=4,6 cm

Wysokość użyteczna przekroju

d

=h – a

1

=60,0 – 4,6=55,4 cm

Współczynnik wejściowy



eff

=

M

Sd

b d

2

f

cd

=

220,1

0,3

⋅0,554

2

⋅10,6⋅10

3

=0,226

Względna efektywna wysokość strefy ściskanej



eff

=1 –



1 – 2



eff

=1 –



1 – 2

⋅0,226 =0,273



eff

=0,273

eff , lim

=0,53

przekrój pojedynczo zbrojony



eff

=1 – 0,5

eff

=1 – 0,5⋅0,273=0,863

Wymagane pole przekroju zbrojenia

A

s1 , req

=

M

Sd



eff

d f

yd

=

220,1

0,863

⋅0,554⋅350⋅10

3

=13,45⋅10

−4

m

2

=13,45 cm

2

Minimalne pola przekroju zbrojenia elementu zginanego

A

s min

=0,0013b d=0,0013⋅0,3⋅0,554=2,11⋅10

−4

m

2

=2,11 cm

2

A

s min

=0,26

f

ctm

f

yk

b d

=0,26

1,9

410

0,3

⋅0,554=1,96⋅10

−4

m

2

=1,96 cm

2

Minimalne pole przekroju zbrojenia z uwagi na ograniczenie szerokości rys do

wartości

w

k

=0,3mm

Współczynnik uwzględniający rozkład naprężeń w przekroju w chwili poprzedzającej

zarysowanie

k

c

=0,4

– zginanie

Współczynnik

uwzględniający

wpływ

nierównomiernych

naprężeń

samorównoważących się w ustroju

k

=0,5

0,8 – 0,50,8 – h

0,8 – 0,3

=0,5

0,8 – 0,30,8 – 0,6

0,8 – 0,3

=0,62

Pole rozciąganej strefy przekroju w chwili poprzedzającej zarysowanie

A

ct

=0,5b h=0,5⋅0,3⋅0,6=0,09 m

2

Średnia wytrzymałość betonu na rozciąganie w chwili spodziewanego zarysowania

f

ct , eff

= f

ctm

=1,9 MPa

Naprężenie w zbrojeniu natychmiast po zarysowaniu – tablica 12 PN



s , lim

=200

240 – 200 25 – 

25 – 16

=200 

 240 – 200 25 – 20

25 – 16

=222,2 MPa

A

s , min

=k

c

k f

ct , eff

A

ct



s , lim

=0,4⋅0,62⋅1,9

0,09

222,2

=1,91⋅10

−4

m

2

=1,91 cm

2

Przyjęto zbrojenie podłużne:

• dołem:

5

 20

ze stali A-III (34GS) o polu

A

s1, prov

=15,71 cm

2

,

• górą:

2

12

ze stali A-I (St3SX-b) o polu

A

s1

=2,26 cm

2

.

Sprawdzenie możliwości umieszczenia

5

 20

w jednej warstwie

b

min

=2 c

nom

2

s

5 4 s

1

=2⋅302⋅65⋅204⋅25=252 mmb=300 mm

Wymiarowanie zbrojenia poprzecznego z uwagi na ścinanie

Nośność na ścinanie odcinka I-go rodzaju – element zginany

Założono doprowadzenie do podpory 2 prętów

 20

co stanowi mniej niż 50%

wymaganego zbrojenia w przęśle.

k

=1,0

Stopień zbrojenia dla

2

 20

o polu

A

sL

=6,28 cm

2



L

=

A

sL

b d

=

6,28

⋅10

−4

0,3

⋅0,554

=0,0040,01

V

Rd1

=[0,35 k f

ctd

1,240 

L

]b d =

=[0,35⋅1,0⋅0,87⋅10

3

1,240⋅0,004 ]0,3⋅0,554=68,4 kN

Jeżeli zachodzi bezpośrednie przekazywanie obciążenia belki lub płyty na podporę ,

tzn. jeżeli reakcja podpory działa na dolną krawędź elementu, a równocześnie

rozłożone obciążenie dział a na górną krawędź elementu, to przy sprawdzaniu

warunków

V

Sd

V

Rd1

i

V

Sd

V

Rd3

na odcinku przypodporowym można zamiast

V

Sd

przyjąć największą (co do wartości bezwzględnej) siłę poprzeczną

występującą w odległości

d

od krawędzi podpory.

Charakterystyczne wartości siły poprzecznej

• w odległości

d

od krawędzi podpory –

V

Sd , a

n

d

V

Sd , a

n

d

=V

Sd , max

– q

o

a

n

d =146,73 – 48,91 0,190,554=110,34 kN

• na krawędzi podpory –

V

Sd , a

n

V

Sd , a

n

=V

Sd , max

– q

o

a

n

=146,73 – 48,91⋅0,19=137,44 kN

Długość odcinka II-go rodzaju

L

t

=

V

Sd , a

n

−V

Rd1

q

o

=

137,44 – 68,4

48,91

=1,412 m

Nośność na ścinanie na odcinku II-go rodzaju

Współczynnik efektywności betonu przy ściskaniu

=0,6 1 –

f

ck

250

=0,6 1 –

16

250

=0,562

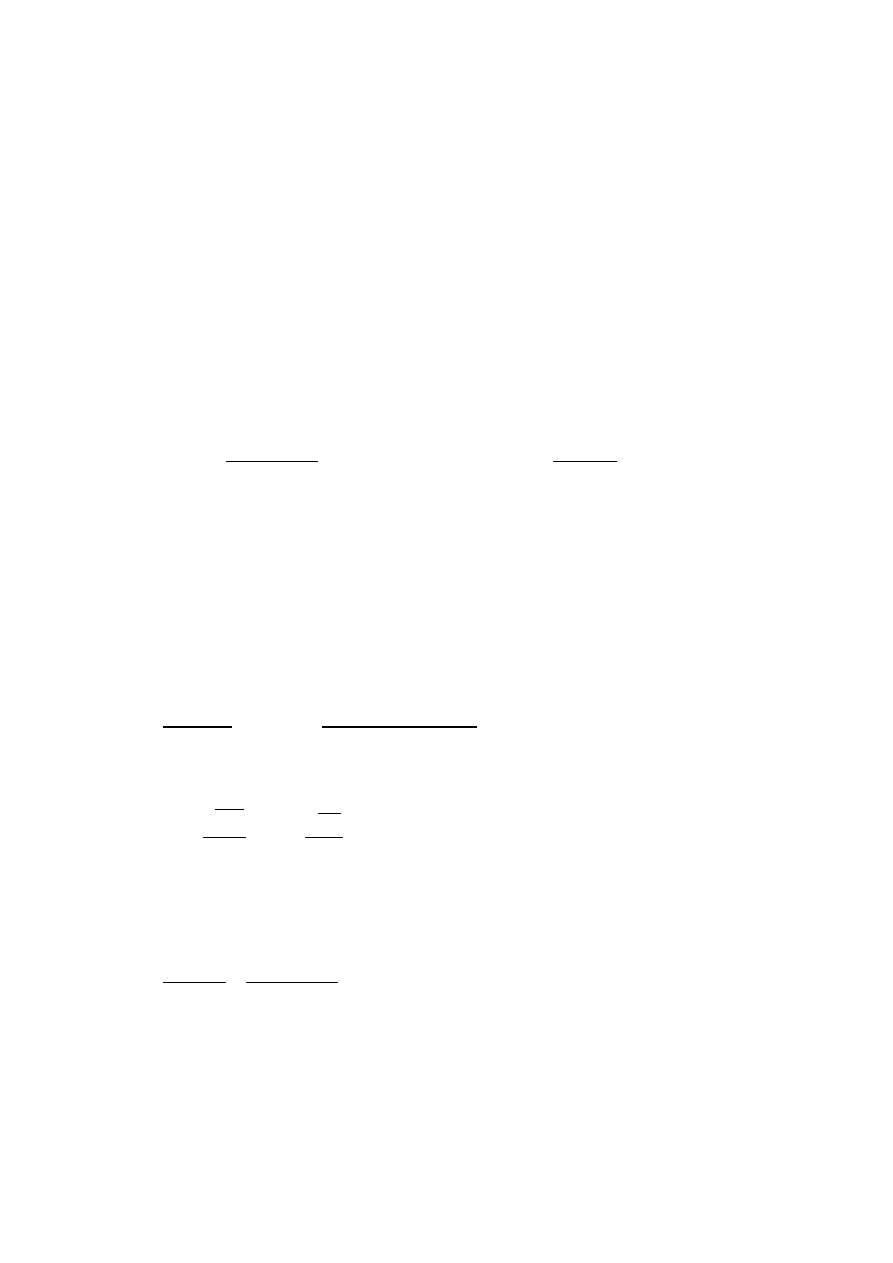
Ramię sił wewnętrznych przy ścinaniu (wysokość strefy ścinania)

z

=0,9 d =0,9⋅0,554=0,499 m

Zgodnie z zaleceniami normy cotangens kąta pochylenia krzyżulców betonowych

powinien odpowiadać wartościom

1,0

cot 2,0

.

Przyjęto:

cot

=1,5

Nośność

V

Rd2

na odcinku I-go rodzaju

V

Rd2

=0,5 f

cd

b z

=0,5⋅0,562⋅10,6⋅10

3

⋅0,3⋅0,499=445,9 kN

V

Sd , a

n

d

=110,34V

Rd2

=445,9 kN

Nośność V

Rd2

w przypadku zbrojenia strzemionami pionowymi

V

Rd2

= f

cd

b z

cot



1

cot

2



=0,562⋅10,6⋅10

3

⋅0,3⋅0,499

1,5

1

1,5

2

=410,97 kN

V

Sd , max

=146,73 kN V

Rd2

=410,97 kN

Określenie wymaganego rozstawu strzemion pionowych

Założono strzemiona:

•

dwucięte ze stali A-I (St3SX-b) o polu

A

sw

=0,56 cm

2

Maksymalny rozstaw strzemion na odcinku II-go rodzaju

s

w , max

=

A

sw

f

yd

V

Sd , a

n

d

z cot

=

0,56

⋅10

−4

210

⋅10

3

110,34

0,499

⋅1,5=0,08 m=8,0 cm

Minimalny stopień zbrojenia poprzecznego



w , min

=0,08



f

ck

f

yk

=0,08



16

240

=0,0013

Maksymalny rozstaw strzemion z uwagi na minimalny stopień zbrojenia

poprzecznego

s

w , max

=

A

sw



w , min

b

=

0,56

⋅10

−4

0,0013

⋅0,3

=0,14 m=14,0 cm

Maksymalne rozstawy strzemion z uwagi na bezpieczne przeniesienie sił

wewnętrznych bez nadmiernych odkształceń tego zbrojenia

s

w , max

=0,75 d =0,75⋅0,554=0,415 m=41,5 cm

s

w , max

=40,0 cm

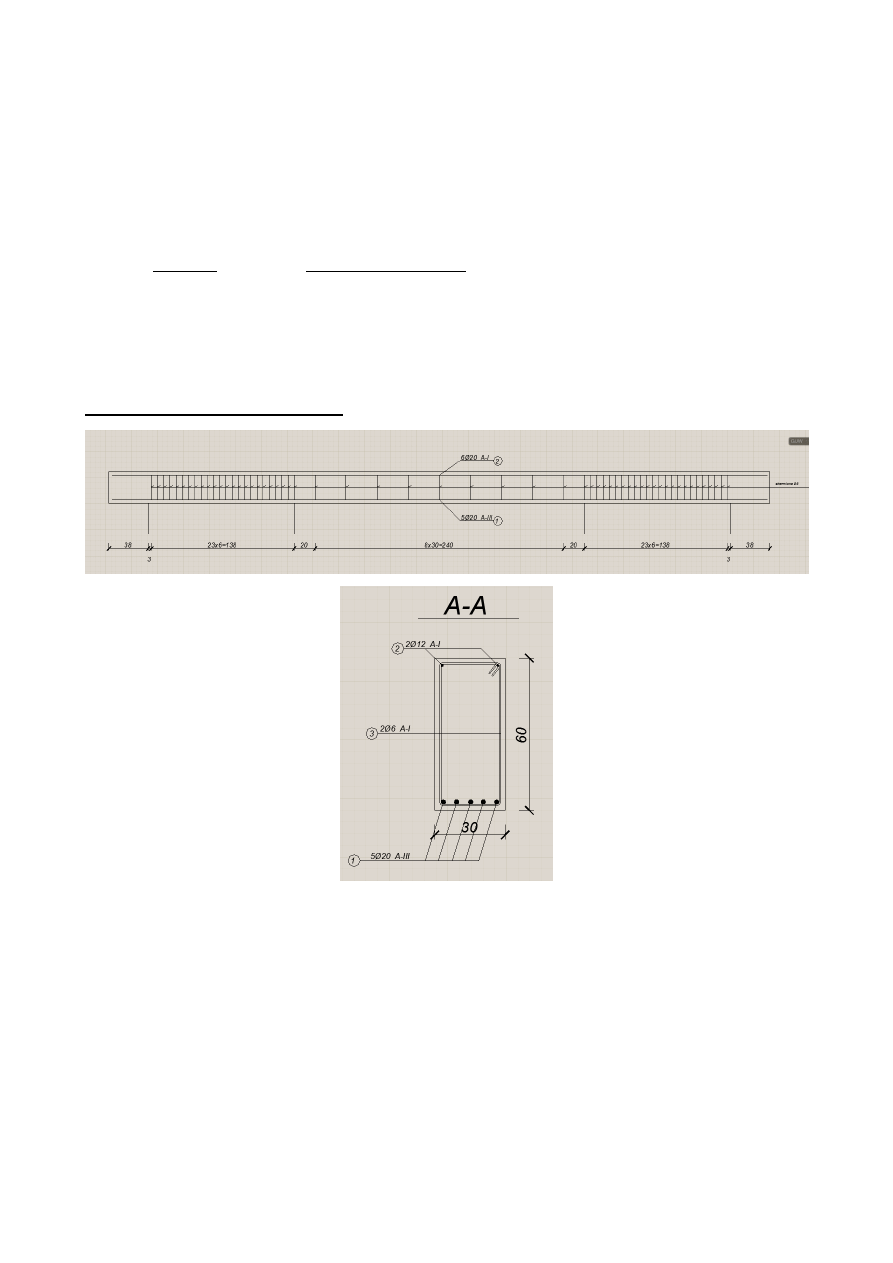
Przyjęto rozstawy strzemion:

• na odcinku I-go rodzaju

s

w

=30,0 cm

,

• na odcinku II-go rodzaju

s

w

=6,0 cm

.

Nośność zbrojenia poprzecznego

V

Rd3

V

Rd3

=

A

sw

f

yd

s

w

z cot

=

0,56

⋅10

−4

⋅210⋅10

3

0,06

0,499

⋅1,5=146,6 kN

V

Sd , a

n

d

=110,34 kN V

Rd3

=146,6 kN

Rozmieszczenie zbrojenia belki

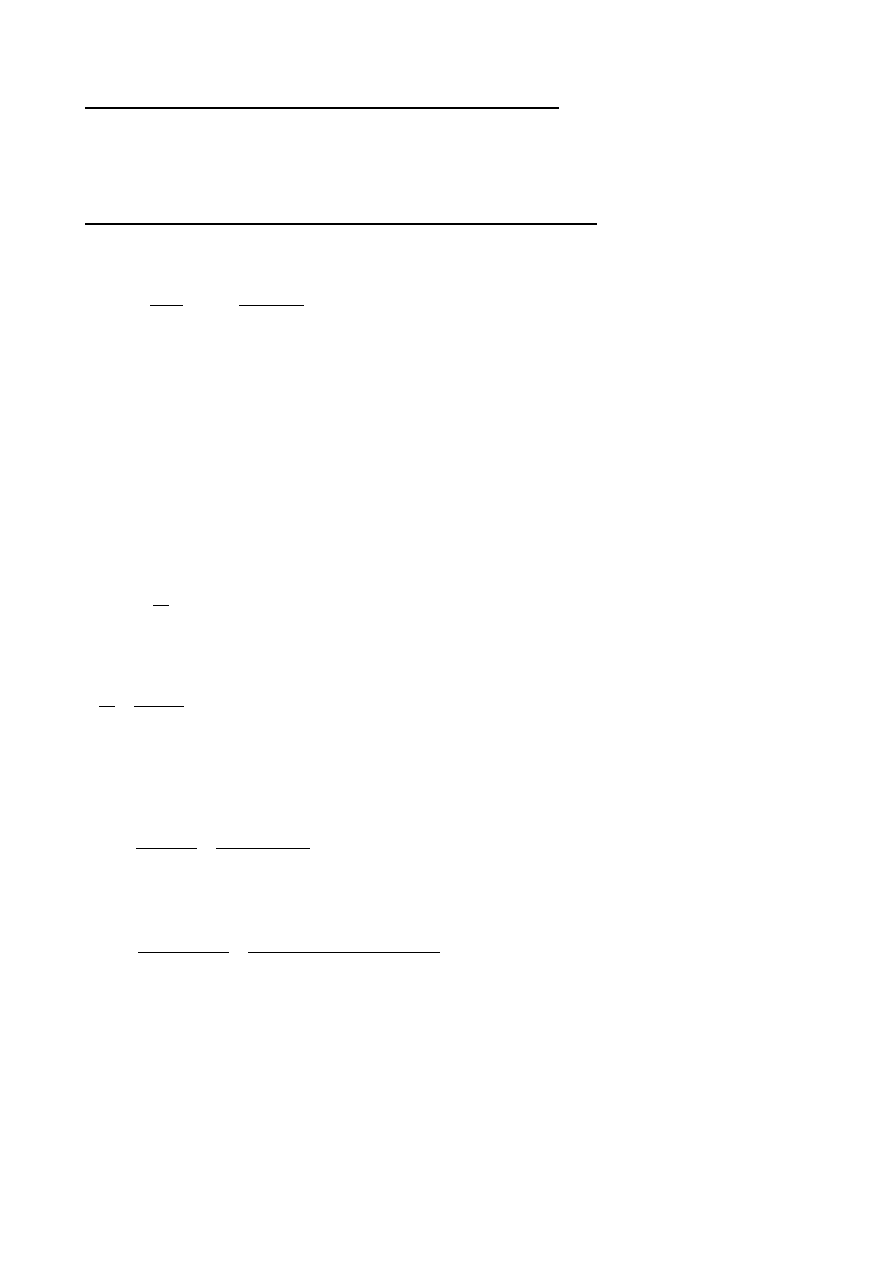
Sprawdzenie warunków stanu granicznego użytkowania

Dopuszczalna szerokość rozwarcia rys belki pracującej w klasie ekspozycji XC2

w

lim

=0,3mm

Sprawdzenie stanu granicznego rozwarcia rys prostopadłych

Moment rysujący

M

cr

=

b h

2

6

f

ctm

=

0,3 0,6

2

6

1,9

⋅10

3

=34,2 kNm

M

Sd , k

=186,75 kNmM

cr

=34,2 kNm

Belka ulega zarysowaniu.

Warunki korzystania z metody uproszczonej obliczania szerokości rozwarcia rys:

• przekrój jest prostokątny,

• zbrojenie stalą żebrowaną ,

•

w

lim

=0,3mm

,

•

d

h

=0,85÷0,95 .

d

h

=

0,554

0,6

=0,923

Wszystkie warunki zostały spełnione.

Stopień zbrojenia podłużnego



L

=

A

s1 , prov

b d

=

15,71

⋅10

−4

0,3

⋅0,554

=0,0090,01

=0,85

Naprężenia w zbrojeniu rozciąganym



s

=

M

Sd , k

 d A

s1 , prov

=

186,75

0,85

⋅0,554⋅15,71⋅10

−4

=252⋅10

3

kPa

=252 MPa

Maksymalna średnica prętów, przy której nie wystąpi przekroczenie dopuszczalnej

wartości rys prostopadłych wynosi



max

=32 mm=20 mm .

WNIOSEK:

Dopuszczalna szerokość rys nie zostanie przekroczona.

Sprawdzenie stanu granicznego rozwarcia rys ukośnych

Z uwagi na wystąpienie odcinków II-go rodzaju wymagane jest sprawdzenie

rozwarcia rys ukośnych.

Miarodajna do obliczeń charakterystyczna wartość siły poprzecznej

V

Sdk , a

n

d

V

Sdk , a

n

d

=V

Sd , k

– q

k

a

n

d =124,5 – 41,50,190,554=93,62 kN

Naprężenia w przekroju miarodajnej siły poprzecznej

=

V

Sdk , a

n

d

b d

=

93,62

0,3

⋅0,554

=563 kPa=5,63 MPa

Stopień zbrojenia poprzecznego na odcinku II-go rodzaju



w1

=

A

sw

s

w

b

=

0,56

⋅10

−4

0,06

⋅0,3

=0,003

Stopień zbrojenia prętami odgiętymi



2

=20 mm



w2

=0

Współczynniki zależne od przyczepności zbrojenia do betonu



1

=1,0

,



2

=0,7

=

1

3



w1



1



s





w2



2



2

=

1

3

0,0031

1,0

⋅0,006



0

0,7

⋅0,02

=0,643

Obliczeniowa szerokość rysy ukośnej

w

k

=

4



2





w

E

s

f

ck

=

4

⋅563⋅0,643

0,0031

⋅210⋅10

6

⋅16⋅10

3

=8,196⋅10

−5

m

=0,08 mm

w

k

=0,08 mmw

lim

=0,3 mm

WNIOSEK:

Dopuszczalna szerokość rys ukośnych nie zostanie przekroczona.

Sprawdzenie stanu granicznego ugięcia

Dopuszczalne ugięcie belki o rozpiętości

L

eff

6,0 m

a

lim



L

eff

200

=

600

200

=3,0 cm=30,0 mm

Stopień zbrojenia podłużnego



L

=0,009 .

Naprężenia w zbrojeniu rozciąganym



s

=252 MPa

Współczynniki korekcyjne



1

=1,0



2

=

250



s

=

250

252

=0,99



3

=1,0

Wskaźnik



L

eff

d



max

=18

- tablica 13

L

eff

d

=

600

55,4

=10,83

1



2



3



L

eff

d



max

=1,0⋅0,99⋅1,0⋅18=17,82

WNIOSEK:

Warunek został spełniony ugięć można nie sprawdzać.

Sprawdzenie szerokości rozwarcia rys prostopadłych metodą dokładną

Dopuszczalna szerokość rys prostopadłych

w

lim

=0,3mm

Moment rysujący

M

cr

=

b h

2

6

f

ctm

=

0,3

⋅0,6

2

6

1,9

⋅10

3

=34,2 kNm

M

Sd , k

=186,75 kNmM

cr

=34,2 kNm

Belka ulega zarysowaniu.

Określenie współczynnika pełzania

Założono:

t

0

=28 dni – wiek betonu w chwili obciążenia

t – t

0

 ∞ - czas trwania obciążenia

RH

=50

% – wilgotność środowiska

Miarodajny wymiar przekroju elementu

h

0

=

2A

c

u

=

2 b h

b

2 h

=

2

⋅300⋅600

300

2⋅600

=240 mm

Współczynniki zależne od średniej wytrzymałości betonu na ściskanie i wilgotności

środowiska – f

cm

35 MPa



RH

=1

1 –

RH

100

0,1

3



h

0

=1

1

−

50

100

0,1

3



240

=1,805

 f

cm

=

16,8



f

cm

=

16,8



24

=3,429

t

0

=

1

0,1

t

0

0,2

=

1

0,1

28

0,2

=0,488

Końcowy współczynnik pełzania

∞ ,t

0

=

RH

 f

cm

 t

0

=1,805⋅3,429⋅0,488=3,023

Funkcja określająca przyrost pełzania po przyłożeniu obciążenia



c

t – t

0

=1,0 dla t−t

0

 ∞

Współczynnik pełzania betonu

t ,t

0

=∞ , t

0

 

c

t – t

0

=3,023⋅1,0=3,023

Efektywny moduł sprężystości betonu

E

c , eff

=

E

cm

1

t – t

0



=

29000

1

3,023

=7209 MPa

Współczynnik wpływu pełzania dla obciążeń długotrwałych do wyznaczenia relacji

modułów sprężystości podłużnej stali i betonu



e , t

=

E

s

E

c , eff

=

200000

7209

=27,74

Stopień zbrojenia podłużnego:



L

=

A

s1 , prov

b d

=

15,71

30,0

⋅55,4

=0,009

Wysokość strefy ściskanej obliczona na podstawie teorii fazy II dla obciążeń

długotrwałych

x

II

=d [





L



e , t

2

L



e , t

−

L



e , t

]=

=0, 554 [



0,009

⋅27,74  20,009⋅27,74−0,009⋅27,74 ]=0,281 m=28,1 cm

Współczynnik wyrażający stosunek obliczeniowej rysy do szerokości średniej

=1,7=

1,7 – 1,30,8−h

0,8 – 0,3

=1,7 –

1,7 – 1,30,8 – 0,6 

0,8 – 0,3

=1,54

Efektywne pole przekroju strefy rozciąganej

h

eff

=min

{

2,5 a

1

=2,5⋅0,046 =0,115 m

h – x

II

3

=

0,6 – 0,281

3

=0,106 m

}

=0,106 m

A

ct , eff

=b h

eff

=0,3⋅0,106 =318,6⋅10

−4

m

2

Efektywny stopień zbrojenia



r

=

A

s1 , prov

A

ct , eff

=

15,71

⋅10

−4

0,0319

⋅10

−4

=0,049

Współczynnik zależny od przyczepności prętów zbrojenia

k

1

=0,8

- pręty żebrowane

Współczynnik zależny od rozkładu odkształceń w strefie rozciąganej

k

2

=0,5

– trójkątny rozkład przy zginaniu

Średni rozstaw rys w elemencie zginanym

s

rm

=500,25 k

1

k

2





r

=500,25⋅0,8⋅0,5

20

0,049

=91 mm

Współczynnik zależny od przyczepności prętów zbrojenia



1

=1,0

– pręty żebrowane

Współczynnik zależny od czasu działania i powtarzalności obciążenia



2

=0,5

– obciążenia długotrwałe

Naprężenie w zbrojeniu rozciąganym obliczone w przekroju przez rysę



s

=

M

Sd , k

A

s1 , prov

d –

x

II

3



=

186,75

15,71

⋅10

−4

0,554 –

0,281

3



=258⋅10

3

kPa

=258 MPa

Średnie odkształcenie zbrojenia rozciąganego



sm

=



s

E

s

[1−

1



2



M

cr

M

Sd , k



2

]=

258

200000

[1 – 0,5⋅1,0

34,2

186,75



2

]=0,0013

Szerokość rozwarcia rys prostopadłych

w

k

= s

rm



sm

=1,54⋅91⋅0,0013=0,18 mm

w

k

=0,18 mmw

k , lim

=0,3 mm

WNIOSEK:

Dopuszczalna szerokość rozwarcia rys prostopadłych nie została przekroczona.

Sprawdzenie ugięcia

Moment bezwładności przekroju zarysowanego

J

II

=

b x

II

3

3



e , t



L

b d

 d – x

II



2

=

=

0,3

⋅0,28163

3

27,74⋅15,71⋅10

−4

⋅0,3⋅0,554 0,554 – 0,281

3

=

=546706⋅10

−8

m

4

=546706 cm

4

Położenie osi obojętnej w przekroju niezarysowanym (faza I)

x

I

=

0,5 b h

2



e , t

A

s1 , prov

d

b h



e , t

A

s1 , prov

=

0,5

⋅0,3⋅0,6

2

27,74⋅15,71⋅10

−4

⋅0,554

0,3

⋅0,55427,74⋅15,71⋅10

¿

4

=0,35 m

Moment bezwładności przekroju niezarysowanego

J

I

=

b h

3

12

b h x

I

– 0,5 h



2



e , t

A

s1 , prov

 d – x

I



2

=

=

0,3

⋅0,6

3

12

0,3⋅0,6 0,35 – 0,5⋅0,6

2

27,74⋅15,71⋅10

−4

0,554 – 0,35

2

=

=7663374⋅10

−8

m

4

=7663374 cm

4

Sztywność przekroju, w którym osiąga się

M

Sd

B

∞

=

E

c , eff

J

II

1

−

1



2



M

cr

M

Sd , k



2

1 –

J

II

J

I



=

7209

⋅10

3

⋅546706⋅10

−8

1 – 1,0

⋅0,5

34,2

186,75



2

1 –

546706

⋅10

−8

7663374

⋅10

−8



=

=39602,7 kNm

2

Wartość ugięcia

a

k

=

5

48

M

Sd , k

L

eff

2

B

∞

=

5

48

186,75

⋅6,0

2

39602,7

=0,0177 m=1,77 cm=18 mm

a

k

=18 mma

lim

=30 mm

WNIOSEK:

Ugięcie nie przekracza wartości dopuszczalnej.