1

  UNIWERSYTET  ŚLĄSKI   W  KYTOWICYCH 

     I PRACOWNIA  FIZYCZNA 

Ć W I C Z E N I E     NR 31 

 
 

  

           POMIYR  CIEPŁY  MOLOWEGO  POWIETRZY 

                  METODĄ ROZŁYDOWYNIY KONDENSYTORY 

    

    

ZAGADNIENIA DO KOLOKWIUM  WSTĘPNEGO 

-gaz doskonały, gaz rzeczywisty, izoprocesy gazu doskonałego 
-I zasada termodynamiki, zasada ekwipartycji energii, liczba stopni swobody 
-pojemność cieplna gazów, ciepła molowe 

c

p

 i  c

v

 

-energia naładowanego kondensatora 
-pomiar ciśnienia gazu metodą manometru cieczowego (U-rurki). 
 
 
OPIS ĆWICZENIA 

Energia  zgromadzona  w  naładowanym  kondensatorze  służy  do  podgrzania    powietrza 
wypełniającego  objętość  izolowanego  zbiornika  (  temosu  ).  Przekaz  energii  następuje  metodą 
rozładowania się kondensatora poprzez spiralę grzejną znajdującą się wewnątrz  termosu. Mierząc 
zmianę ciśnienia powietrza w termosie 

∆p

 przy pomocy manometru cieczowego i znając parametry 

elektryczne kondensatora  możemy obliczyć wartość 

c

v

 dla powietrza. W obliczeniach korzystamy 

z   wykresu  

∆p

 

(U

2

 ) 

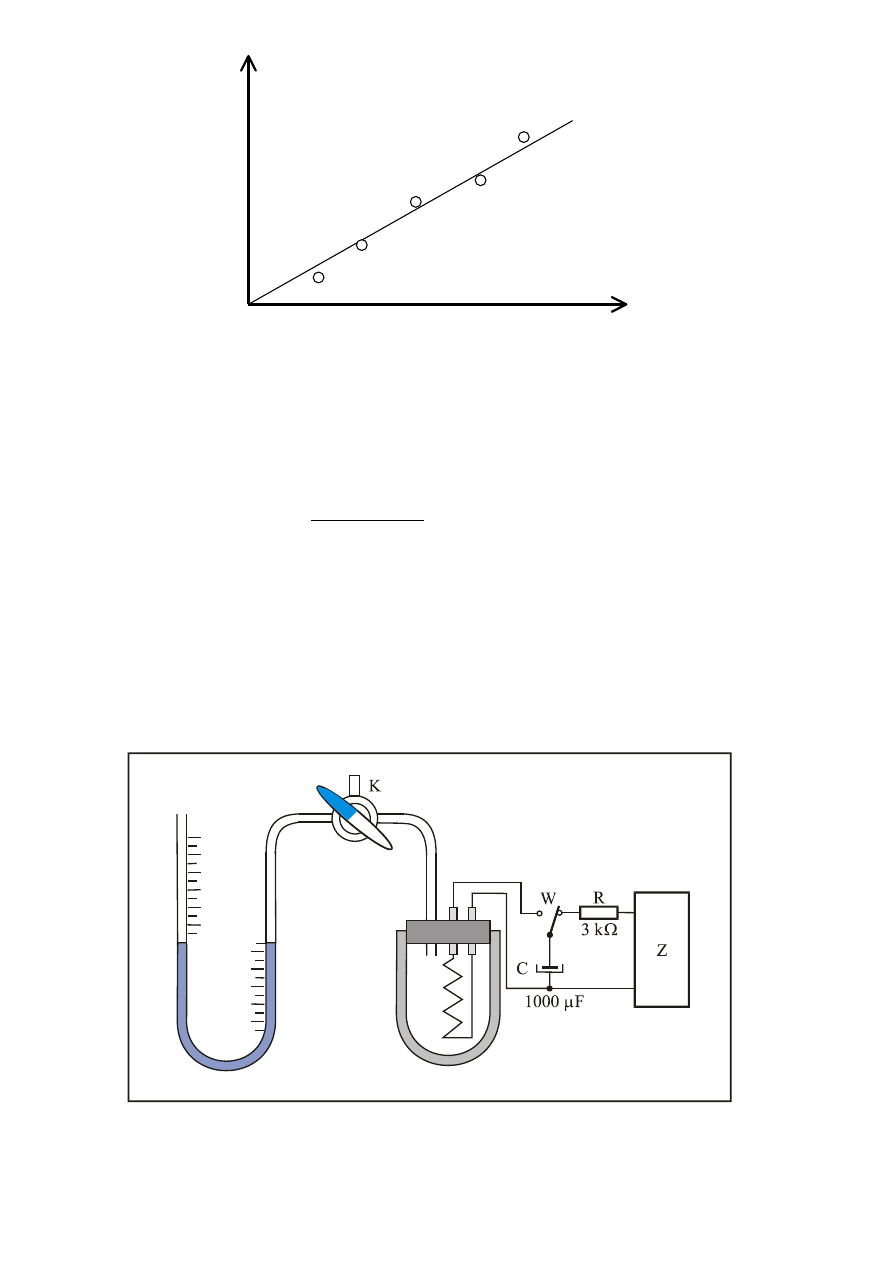
otrzymanego z wyników pomiarowych. Przykładowy wykres zawiera rys. 1. 

 

 

APARATURA 

 

-zestaw do pomiaru ciepła molowego 
-zasilacz prądu stałego 

-dwa przewody wysokonapięciowe 
 

WZORY SCHEMATY  

 

ENERGIA NAŁADOWANEGO KONDENSATORA:  
 
 

                                                  

2

2

1

CU

E

C

=

 

                 

                                                

 

(31. 1.) 

C 

-pojemność kondensatora 

U 

-napięcie 

 
 
 

PRZYROST ENERGII GAZU,  PRZY  V=const. 
 
 

 

2

                                                   

T

C

n

E

v

∆

⋅

⋅

=

∆

                                                             

( 31.2.) 

n 

-ilość moli gazu w objętości V 

C

V 

-ciepło molowe przy V=const. 

∆ 

-przyrost temperatury 

 

 
Z  RÓWNANIA STANU GAZU DOSKONAŁEGO OTRZYMUJEMY: 
 

                                

R

n

V

p

T

⋅

⋅

∆

=

∆

                                                                   

(31.3.)

 

∆p  -przyrost ciśnienia 
V 

-objętość gazu (= 212ml ± 5ml ) 

R 

-stała gazowa ( = 8,31 J/mol

. 

K 

 
 

 

Podstawiając  

( 3.)

 do 

( 2.)

: 

 
 

                         

R

V

p

C

E

V

⋅

∆

⋅

=

∆

                                                            

  

(31.4.) 

 
 
 

SPRAWNOŚĆ POZYSKANIA ENERGII CIEPLNEJ PRZEZ GAZ WYNOSI: 

 
 
 

                                     

C

E

E

∆

=

η

                                                                         

(31.5.)

 

                      

Po podstawieniu  

(  1. )

 i 

(  4. )

  do  

(  5.)

  otrzymujemy: 

 
 
 

                                 

p

U

V

R

C

C

v

∆

⋅

⋅

⋅

=

2

2

η

                                                 

(31.6.) 

 
 

Wartość 

p

U

∆

2

 wyznaczamy z wykresu  / ∆p=(U

2

) / 

 
 
 
 
 
 
 

 

3

 
 
 
 
 
 
 
 
 
 
 
 
 
 

Rys.1. Przykładowy  wykres zależności 

∆∆∆∆p

 

(

U

2

 ) 

.

 

 

                                    

2

aU

P

=

∆

                                                                  

(31. 7.) 

 

   

 

a

- nachylenie prostej na wykresie zależności ∆

P

=f (U

2

)  

 
  

                    

a

V

R

C

C

V

⋅

⋅

⋅

⋅

=

2

η

                                                         

  

( 31.8.)

 

 

PRZYROST CIŚNIENIA GAZU W OBJĘTOŚCI  V  (

mierzony manometrem cieczowym

 

rys. 2

.)   

WYNOSI: 
 

                                    

h

g

p

⋅

⋅

=

∆

ρ

                                                         

( 31.9.) 

 

 

g = 9,81 m/s

2

               gęstość cieczy w manometrze cieczowym

 

ρ = 700 kg/m

3 

 

 

 

 
                   Rys. 2. Schemat zestawu do pomiaru ciepła molowego powietrza 

∆∆∆∆p

 

U

2

 

 

4

 

 
 
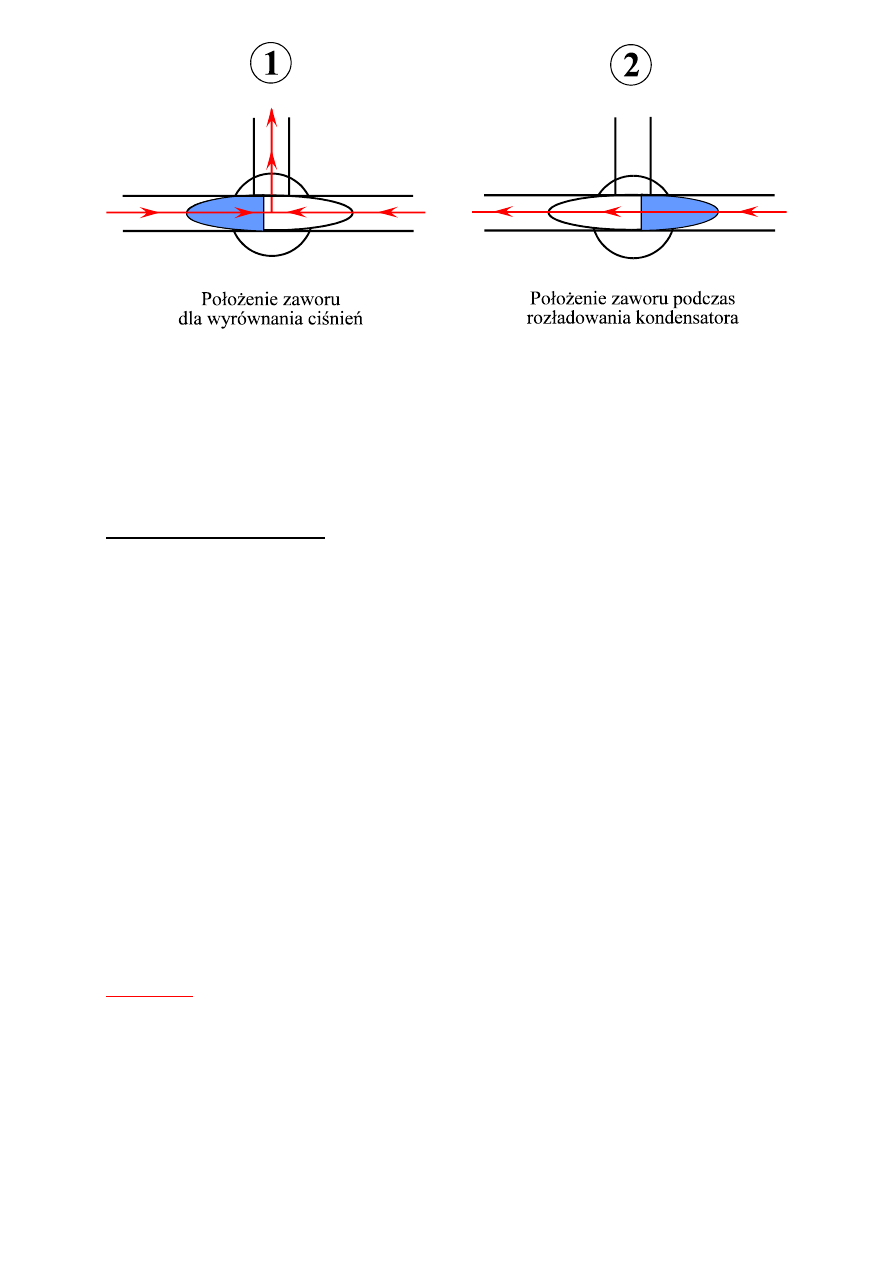
Rys. 3 Schemat przepływu powietrza przez kran trójdrożny w zależności od położenia  

pokrętła zaworu 

 

 
 
 
 
 

WYKONANIE ĆWICZENIA 

 

1. Zapoznać się z   zestawem pomiarowym i   obsługą zaworu kranu trójdrożnego ( rys.3.) 

2. Podłączyć zestaw pomiarowy do zasilacza prądu stałego 

zwracając uwagę na biegunowość! 

3. Wyrównać ciśnienie w objętości 

V

  z ciśnieniem atmosferycznym ( zawór w pozycji 

„1”

). 

4. a) Ustawić w zasilaczu przełącznik odczytu na napięcie 

U

. Ustawić pokrętłem 

W

     

         żądaną  wartość napięcia 

U

min

=100V.

 

    b) Ustawić przełącznik odczytu zasilacza na prąd 

I [mA]

. 

    c) Ustawić przełącznik na płycie zestawu w pozycji 

ŁADOWANIE

, naładować          

        kondensator, aż wskaźnik odczytu prądu zasilacza wskaże minimum 1mA. 

5. Ustawić zawór kranu trójdrożnego w pozycji 

„2” 

6. Rozładować kondensator  (przełącznik w pozycji 

ROZŁADOWANIE

 ), odczytać    

    różnicę poziomów cieczy w manometrze cieczowym

 

h. 

 

7. Czynności z pkt.3-5 wykonać wielokrotnie dla ustalonego napięcia 

U

. 

8. Wykonać pomiary ( pkt.3-8 ) dla kolejnych napięć, aż do 

U

max

=300V.

 

 

UWAGA!!! 

 -w czasie podłączania do zestawu zasilacz powinien być  

WYŁĄCZONY Z SIECI!

 

 

-ostrożnie przekręcać zawór kranu trójdrożnego  (SZKŁO JEST KRUCHE) 

 -ilość pomiarów w pkt.7 i 8 ustalić z prowadzącym na podstawie serii pomiarów próbnych. 

 

 
 

 

5

OBLICZENIA 

 

1.  Dla każdego napięcia obliczyć wartości średnie 

h

 i niepewność pomiarową  

∆∆∆∆h

. 

2.  Korzystając ze wzoru ( 31.9. ) obliczyć wartość przyrostu ciśnienia 

∆∆∆∆p

 i niepewność      

     pomiarową. 

3.  Obliczyć wartość 

U

2

 i niepewność pomiarową 

∆∆∆∆U

2 

. 

4.  Obliczenia z pkt 1-3 powtórzyć dla wszystkich ustalonych napięć. 

5.  Wykreślić zależność 

∆∆∆∆p 

od 

U

2

  

( wg rys. 1.). 

6.  Wyznaczyć nachylenie prostej 

a

  na wykresie  metodą regresji liniowej  i określić  

niepewność pomiarową

 

∆∆∆∆a.

 

7.  Obliczyć wartość ciepła molowego powietrza 

C

v

 ( wzór 31.8.)  i niepewność pomiarową 

∆∆∆∆C

v

, przyjmując   η = 11%. 

 

LITERATURA 
 
1.  S. Szczeniowski, „FIZYKA DOŚWIADCZALNA”, t. II, PWN Warszawa 1972 . 
 

2.  D. Hallidday, R. Resnick, „FIZYKA” ,t.I,  PWN Warszawa 1989. 

 

 

6